异构无线传感器网络覆盖优化算法

杜晓玉孙力娟*②郭 剑韩 崇

(南京邮电大学计算机学院 南京 210003)②(南京邮电大学江苏省无线传感网高技术研究重点实验室 南京 210003)

1 引言

随着无线传感网技术和微电子制造的发展，由大量具有感知能力，计算能力和通信能力的微型传感器节点组成的无线传感器网络被应用到军事领域或民用领域，比如环境监测、工业控制、战场监视、高危环境的探测、生物医学、智能家居及健康监测等[17]-。网络覆盖是无线传感器网络的基本问题之一，它反映了传感器网络节点对指定的监控区域监控程度，在很大程度上影响了网络的成本以及网络在各种具体应用中的性能。

覆盖问题在多机器人系统以及计算几何等领域已进行了广泛的研究。无线传感器网络覆盖问题与计算几何中著名的艺术馆走廊的监控问题和圆周覆盖问题密切相关[4]。艺术馆走廊的监控问题是考虑使用最少数量的摄像机，使得艺术馆走廊内任何角落都能至少被一台摄像机监视。2维平面上的艺术馆走廊监控问题的解决方法是用互不交叠的多个三角形模拟画廊，在每个三角形的任意一个顶点上安装一台摄像机就可以解决此问题， 但3维空间中此问题是一个NP完全问题[4]。监测区域的边界覆盖研究是栅栏覆盖研究的一个特例，文献[1]研究了圆形区域边界的节点覆盖调度问题，通过计算与区域边界相交的感知圆对监测区域的张角来计算覆盖整个圆周所需的最小数目的传感器节点。在一些无线传感器网络的监测应用中，随机部署的传感器节点不需要完全覆盖全部的监测区域，只需要监测区域内的多个重点对象，这类问题称为多目标覆盖问题[5,6]。文献[5]设计了一个传感器节点的感知能耗模型并针对此模型，提出一种启发式分布贪婪算法来解决多目标覆盖问题，该算法以最大化覆盖目标的数量为优化目标建立数学模型，通过改变节点优先级的方式调整传感器节点的感知半径，从而节省网络能耗。文献[6]研究了通过调度传感器节点成多个节点集合，使得网络的生存寿命最长，且连通的目标覆盖问题，要求每个节点集合中的传感器节点既能覆盖目标，又能连通所有的活动传感器节点和汇聚节点。基于虚拟力的覆盖算法也是目前研究的热点[72]-1，虚拟力算法的核心思想是假定传感器节点部署在虚拟力场中，节点与节点，移动节点与目标区域边界之间存在相互作用力，并基于运动图式理论来共同控制移动节点的运动，实现覆盖的优化。

异构无线传感器网络的异构特性体现在节点异构性、链路异构性和网络协议异构性3方面[10,1316]-。其中节点异构性又包括感知能力、计算能力、通信能力和能量等方面的异构性，通信能力、感知能力和能量对覆盖的影响最大。现有文献中关于随机部署的异构无线传感器网络覆盖问题的研究非常少，受到简单随机抽样[17]和最优化算法[17,18]的启发，针对异构传感网络节点初始随机部署时产生覆盖盲区的问题，本文提出了一种基于采样的异构传感网覆盖优化算法(Coverage Optimization algorithm based on Sampling for Homogeneous WSNs , COSH)。以提高网络覆盖率和节点移动距离最小为优化目标，根据采样直线与平面感知圆的交点坐标之间的关系，建立二次优化的数学模型，在节点移动距离最小的情况下达到对直线段的最优覆盖。当监测平面中多条采样直线段可以达到最优覆盖时，平面的覆盖可得到优化。本文主要创新点是： (1)通过对平面的采样，将 2 维平面的覆盖问题转化为 1 维直线的覆盖问题。(2)根据感知圆与采样直线交点坐标建立非线性二次优化数学型，并采取约束条件紧缩的方法，将约束条件转化为线性约束，求解问题的次优解。

2 数学模型及假设

假设监测区域H为矩形，N个半径异构的无线传感器节点随机分布在矩形区域H内，假设无线传感器网络具有以下性质：

(1)传感器节点感知半径异构，即传感器节点具有不同的感知半径，传感器节点的感知模型为二元感知模型，第i个传感器节点iC的位置为，感知半径为。

(2)各传感节点的通信半径是其最大感知半径的两倍，无线传感器网络保证其连通性。

(3)覆盖算法执行之前，节点已准确定位，节点位置坐标已知[19]。

(4)节点在平面上可以自由移动，并节点有充足的剩余能量移动到指定位置。

定义.. 1 采样直线。c为在2维平面中任意一条直线，直线c与监测区域的边界相交于点A和点B。AB为监测平面的采样直线，如图1所示。

定义2 感知圆。传感器节点iC位于2维平面中点，传感半径为ir ，那么由iC所涵盖的感知区域是一个以为圆心，半径为ir的圆，该圆称为感知圆，记为iS ，定义为

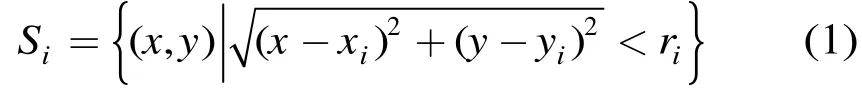
定义3 覆盖率。已覆盖的区域Q的面积S(Q)和节点部署区域H的面积S(H)之比为覆盖率。

3 基于采样的覆盖增强算法

感知圆iS的圆心到采样直线的距离小于感知圆的半径，圆与直线相交所形成的直线段被感知圆覆盖。将与直线相交的感知圆沿直线方向移动，根据感知圆与直线交点坐标建立最优化方程，在节点移动距离最小的情况下，感知圆对直线达到最大覆盖。因此2维平面的覆盖问题可转化为多个采样直线的覆盖优化问题，当多个采样直线达到覆盖优化时，2维监测平面可以达到覆盖增强效果。

如图2所示，矩形EFGH为2维监测平面，分别沿x轴和y轴方向对监测平面进行直线采样，采样直线平行于x轴或者y轴。AB为平面中一条平行于x轴的采样直线，直线方程为为 n个与直线相交的感知圆，对应的传感器节点位置坐标为，其中，感知圆的半径为。假设感知圆点iS与采样直线的交点为，交点坐标满足不等式。称为感知圆点与采样直线的下交点，为上交点，如图3所示。

图 1 采样直线

图 2 异构网采样示意图

图3 感知圆与采样直线相交

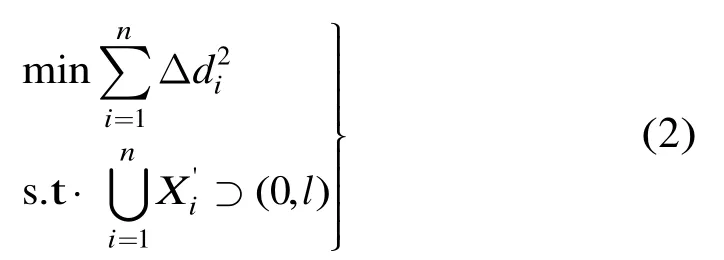
若直线AB被感知圆完全覆盖，每个感知圆与采样直线的下交点位于至少一个感知圆的上交点的左侧，而上交点位于至少一个感知圆的下交点的右侧，同时，至少有一个感知圆的下交点位于左边界的左侧，并且至少有一个感知圆的上交点位于右边界的右侧。约束条件可写为

上述问题为非线性二次规划问题，非常难以求解，采取约束条件紧缩的方法，将约束条件转化为线性的约束条件，求可行解。

定理 1 感知圆顺序不变时，对采样直线完全覆盖所需移动距离之和小于顺序改变时移动的距离之和。

证明 如图4所示，假设在x轴区间(l, 0)内存在有两个感知圆 S1, S2，其圆心分别为。其中。两个感知圆与x轴的交点为和，交点坐标满足如式(4)的不等式。

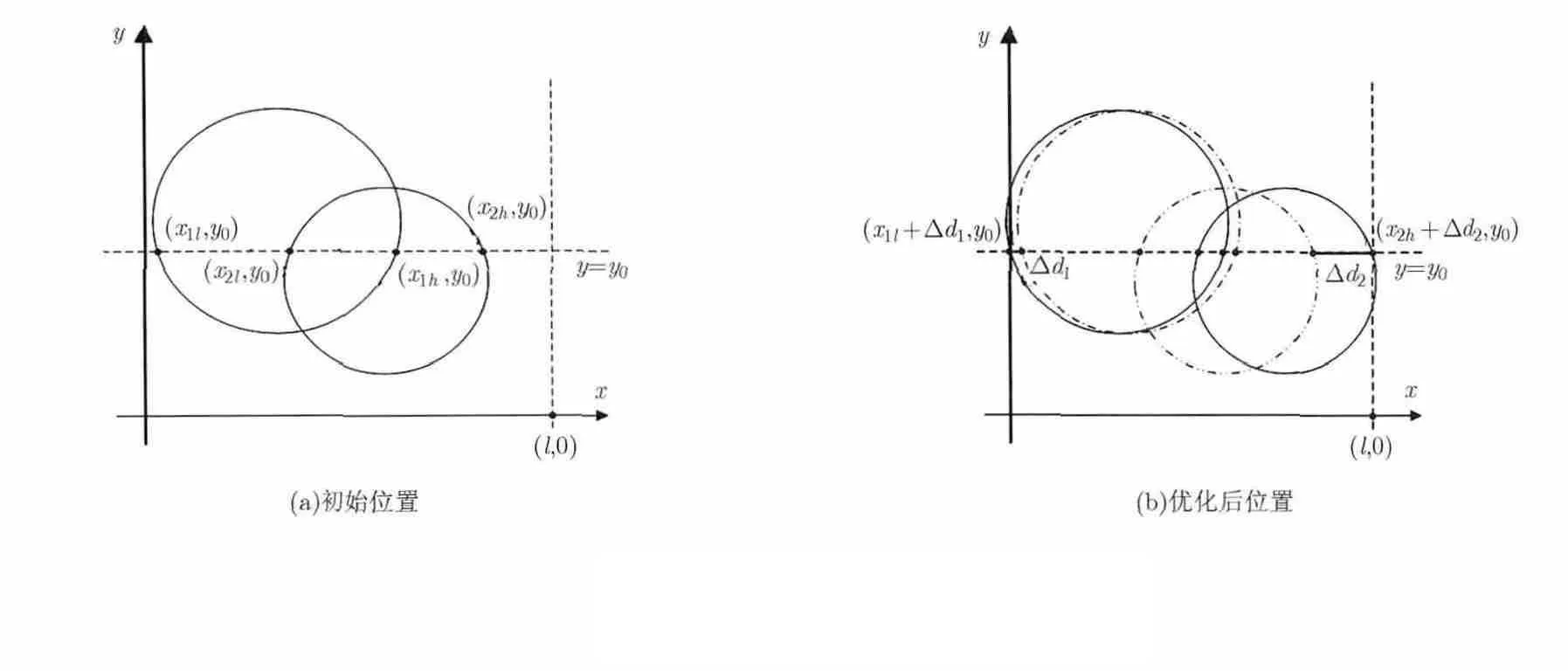
图4 感知圆位置变化图

传感器节点沿直线方向左右移动，若移动之后感知圆对监测区域内的直线完全覆盖，则两感知圆对采样直线的覆盖线段必定存在重叠部分。假设覆盖优化之后感知圆的圆沿x轴的排列顺序未变，则，同时。即此时最小移动距离之和为。

若感知圆沿着 x轴方向的排列顺序发生了变化，优化后节点 1在节点 2右侧，即。同理，根据圆的位置关系可以推导出完全覆盖时最小移动距离之和为，则有根据圆的性质可得

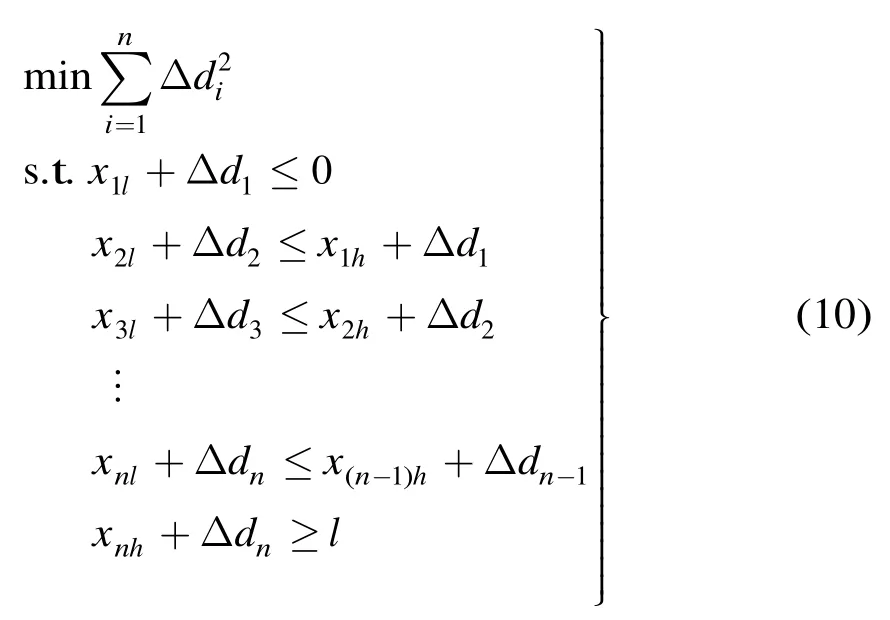
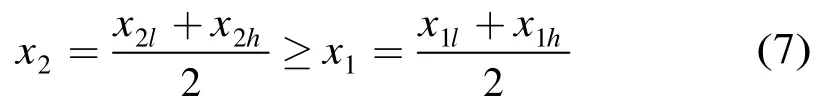
证毕

感知圆iS与直线段相交所形成的线段长度为如图6所示，如果Ll＜，即达不到完全覆盖的理想情况，式(10)的最优化问题无解，此时无法达到最优覆盖。当覆盖圆与直线段AB相交所形成的线段互不相交时，即任意一个感知圆与直线相交的下交点位于前一感知圆的上交点的右侧，而上交点位于下一感知圆的下交点的左侧时，感知圆对直线段的覆盖区域达到最大，最优化算法为, n个感知圆与直线AB相交的线段的总长度L为。如果L大于采样直线的长度l，采样直线可以完全被覆盖，如图5所示，优化之后感知圆在采样直线方向的相对位置顺序不改变，iS与直线段相交的坐标应满足如式(8)和式(9)的不等式：

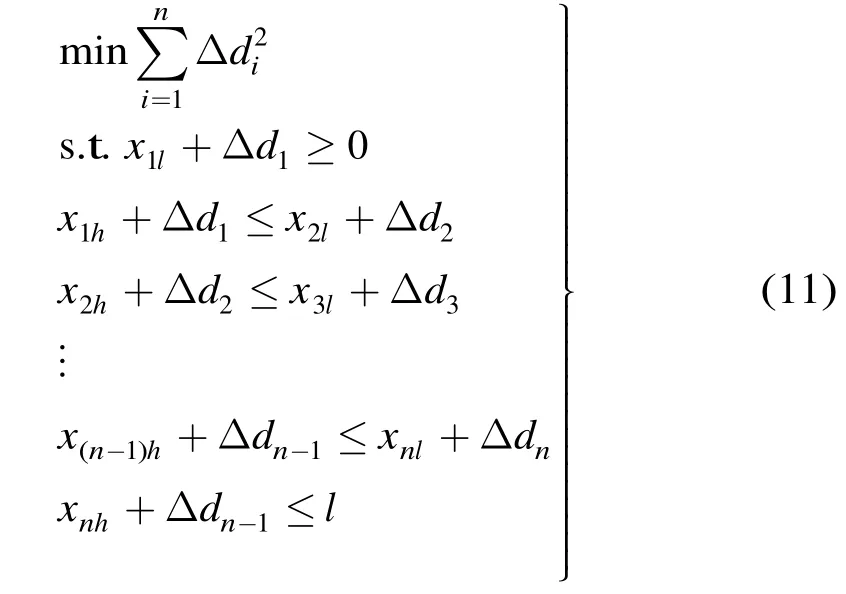
4 算法流程图

N个传感器节点随机分布在长为l，宽为w的区域内，节点半径为

如图 5(b)所示，优化之后感知圆对采样直线完全覆盖，即任意一个感知圆与直线相交的下交点位于前一感知圆的上交点的左侧，而上交点位于下一感知圆的下交点的右侧，优化算法为为所有传感器节点感知半径的最小值，R为传感器节点感知半径的最大值。采样直线的初始位置为，采样的步长为d。单次覆盖优化算法的函数为

图5 L＆gt;l，覆盖优化前后对比图

图6 L＆lt;l，覆盖优化前后对比图

line为采样直线的直线方程，C_n为节点的坐标和半径的集合，E_v为边界参数，是监测区域的边界位置，表示了采样直线最大的采样值。若采样直线的与x轴平行，则直线方程为y=yi, E_v l= ；若与y轴平行，直线方程为x = xj, E_v w= 。集合C为函数的输出，是所有节点新的坐标值。单次覆盖优化算法函数cover的流程图如图7所示。

纵向直线采样的覆盖优化算法与横向采样类似，将算法中对交点的横坐标计算替换为交点的纵坐标计算即可。横向覆盖优化和纵向覆盖优化之间存在相互影响，当采样步长较小时，相邻两条采样直线的优化结果也会相互影响，因此采用多次迭代的方法，使覆盖率达到一个稳定值。算法的伪码如表1所示。

5 仿真分析

图7 单次覆盖优化算法的流程图

表1 COSH算法伪码

为了验证 COSH算法的有效性，本文利用Matlab进行仿真实验。在实验中，无线传感器节点随机分布在长度为300 m，宽度为300 m的部署区域中。节点的最大感知半径R为40 m，最小值感知半径r为15 m，每个传感器节点的感知半径为区间[15,40]内的随机数。图8为40个传感器节点的随机分布在部署区域中的网络布局图，图中数字为节点的ID号。设定采样步长为20 m，经过2次COSH算法的迭代计算，新的网络布局如图9所示。由仿真图可以看出，经过COSH算法优化之后节点较为均匀的分布在监测区域内，覆盖冗余及覆盖盲区的现象均有所减少。

为进一步验证算法的性能，通过实验对文献[7]所提出的虚拟力算法和COSH算法的收敛速度及覆盖率进行比较，图10~图12节点数目分别为40, 50,60时覆盖率随迭代次变化的对比图，图13为随机部署，6次迭代的虚拟力算法和2次迭代的COSH算法覆盖率随传感器节点数量变化的仿真图。由仿真结果可以看出，COSH算法的收敛速度要远远高于虚拟力算法，COSH算法可在3次迭代以内达到最佳覆盖率，但虚拟力覆盖通常经过10次迭代计算才能达到最佳覆盖率，从数据上看，COSH算法覆盖优化效果远高于虚拟力算法。

COSH的覆盖优化效果不仅和迭代次数有关，也受到采样直线步长的影响，图14为COSH算法在不同节点数目的情况下覆盖率随采样步长的变化图。当采样步长较小时，两次采样直线之间距离较小，优化结果会相互影响，因此在计算量增加的情况下覆盖率反而有所下降。采样步长过大时，无法对整个监测区域的覆盖情况进行优化，同样覆盖率也不能得到有效的提高。综合两方面的因素考虑，我们选择采样步长为 /2R 。图15为COSH算法在不同节点数目的情况下，每次迭代优化时节点的平均移动距离的变化图。由图中可以看出算法，第 1次迭代优化移动距离最大，随着迭代次数的增加，节点的平均移动距离减少，并收敛于稳定值。这表明算法的收敛速度很快，经过2~3次迭代就可以达到较优的覆盖效果。结合图10~图13分析，3次迭代之后节点位置在小范围内微调，但对覆盖率的提高影响不大，在满足覆盖要求的前提下算法可在 3次迭代之内完成。

图 8 随机分布网络布局图

图9 COSH算法网络布局

图10覆盖率随迭代次数的变化(40个节点)

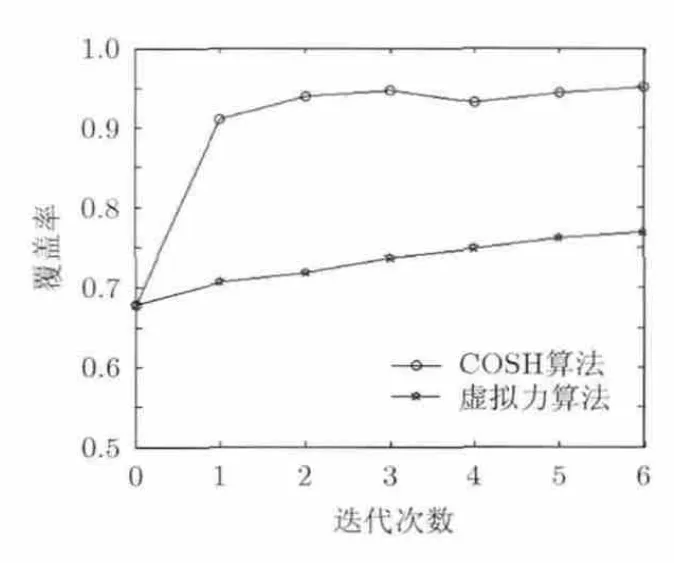
图11覆盖率随迭代次数的变化(50个节点)

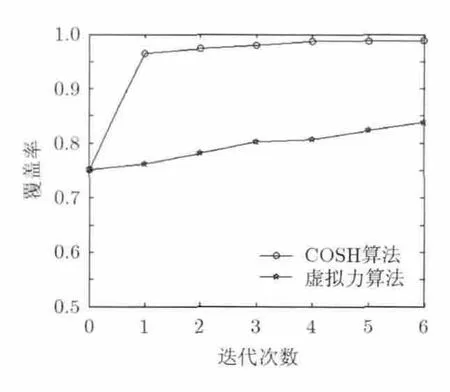
图12覆盖率随迭代次数的变化(60个节点)

图13 覆盖率随节点数量的变化

图14 覆盖率随采样步长的变化

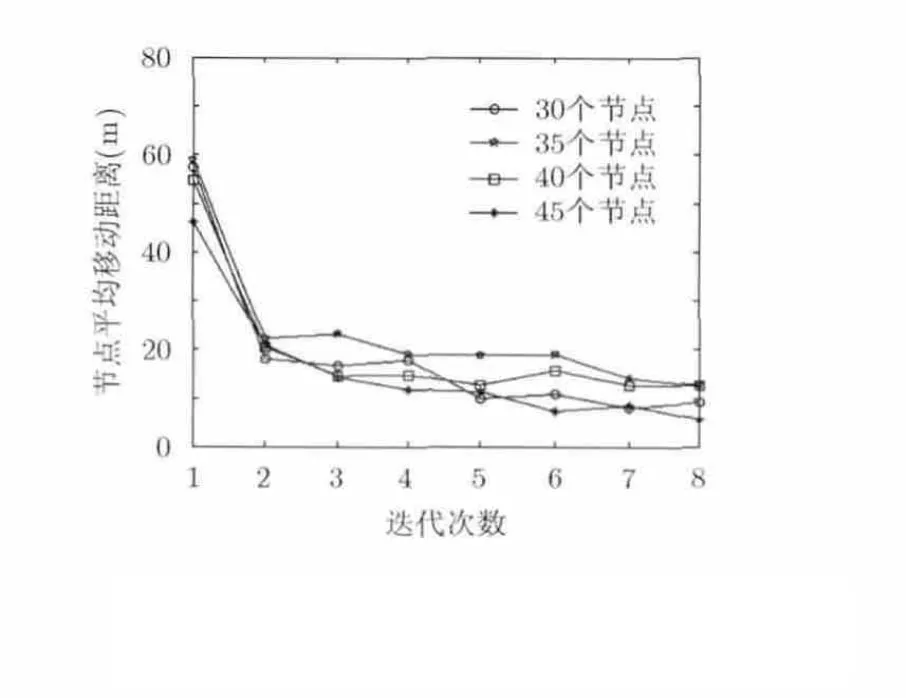
图15 平均节点移动距离随迭代次数的变化

6 结束语

针对异构传感网络节点初始随机部署时产生覆盖盲区的问题，本文提出一种适用于异构网络的采样覆盖优化算法。通过对监测平面进行直线采样，对采样直线的覆盖进行优化。根据直线段与平面感知圆的交点坐标之间的关系，以提高网络覆盖率和节点移动距离最小为优化目标，建立二次优化的数学模型，在节点移动距离最小的情况下达到对直线段的最优覆盖。多条采样直线段可以达到最优覆盖时，平面的覆盖可得到优化。由实验结果可以看出，该算法可有效地提高异构网的覆盖率。经过2~3次迭代计算，异构网的覆盖率可提高20%左右，并且该算法的收敛速度和覆盖的优化效果要高于普通的优化算法。

[1] Khedr A M and Osamy W. Minimum perimeter coverage of query regions in a heterogeneous wireless sensor network[J].Information Sciences, 2011, 181(15): 3130-3142.

[2] Bai Xiao-le, Yun Zi-qiu, Dong Xuan, et al.. Optimal multiple-coverage of sensor networks[C]. 30th IEEE International Conference on Computer Communications,Joint Conference of the IEEE Computer and Communications Societies (INFOCOM 2011), Shanghai,2011: 2498-2506.

[3] Ammari H M and Das S K. A study of k-coverage and measures of connectivity in 3D wireless sensor networks[J].IEEE Transactions on Computers, 2010, 59(2): 243-257.

[4] Marengoni M I C, Draper B A, Hanson A, et al.. A system to place observers on a polyhedral terrain in polynomial time[J].Image and Vision Computing, 2000, 18(10): 773-780.

[5] Qun Zao and Gurusamy M. Lifetime maximization for connected target coverage in wireless sensor networks[J].IEEE/ACM Transactions on Networking, 2008, 16(6):1378-1391.

[6] Naderan M, Dehghan M, and Pedram H. Sensing task assignment via sensor selection for maximum target coverage in WSNs[J]. Journal of Network and Computer Applications,2013, 36(1): 262-273.

[7] Yi Zou and Chakrabarty K. Sensor deployment and target localization based on virtual forces[C]. The 22nd Annual Joint Conference of the IEEE Computer and Communications Societies, San Francisco, USA, 2003:1293-1303.

[8] 周浦城, 崔逊学, 王书敏, 等. 基于虚拟力的无线传感器网络覆盖增强算法[J]. 系统仿真学报, 2009, 21(5): 1416-1419.Zhou Pu-cheng, Cui Xun-xue, Wang Shu-min, et al.. Virtual force-based wireless sensor network coverage-enhancing algorithm[J]. Journal of System Simulation, 2009, 21(5):1416-1419.

[9] 李明, 石为人. 虚拟力导向差分算法的异构移动传感网络覆盖策略[J]. 仪器仪表学报, 2011, 32(5): 1043-1051.Li Ming and Shi Wei-ren. Virtual force-directed differential evolution algorithm based coverage-enhancing algorithm for heterogeneous mobile sensor networks[J]. Chinese Journal of Scientific Instrument, 2011, 32(5): 1043-1051.

[10] 黄帅, 程良伦. 一种基于虚拟力的有向传感器网络低冗余覆盖增强算法[J]. 传感器技术学报, 2011, 24(3): 418-422.Huang Shuai and Cheng Liang-lun. A low redundancy coverage-enhancing algorithm for directional sensor network based on fictitious force[J]. Chinese Journal of Sensors and Actuators, 2011, 24(3): 418-422.

[11] Huang Jun-jie, Sun Li-juan, Wang Ru-chuan, et al.. Improved virtual potential field algorithm based on probability model in three-dimensional directional sensor networks[J].International Journal of Distributed Sensor Networks, 2012,DOI:10.1155/2012/942080.

[12] Huang Jun-jie, Huang Hai-ping, Sun Peng, et al.. Probability model based coverage-enhancing algorithm for WSNs of nodes’ adjustable movement pattern[J]. International Journal of Distributed Sensor Networks, 2012, DOI:10.1155/2012/570643.

[13] 洪榛, 俞立, 张贵军. 多级异构无线传感网高效动态聚簇策略研究[J]. 自动化学报, 2013, 39(4): 454-460.Hong Zhen, Yu Li, and Zhang Gui-jun. Efficient and dynamic clustering scheme for heterogeneous multi-level wireless sensor networks[J]. Acta Automatica Sinica, 2013, 39(4):454-464.

[14] 李明. 异构传感器网络覆盖算法研究[D]. [博士论文], 重庆大学, 2011.Li Ming. Study on coverage algorithms for heterogeneous wireless sensor networks[D]. [Ph.D. dissertation], Chongqing University, 2011.

[15] Kumar D, Aseri T C, and Patel R B. EEHC: energy efficient heterogeneous clustered scheme for wireless sensor networks[J]. Computer Communications, 2009, 32(4):662-667.

[16] 王明慈, 沈恒范. 概率论与数理统计[M]. 北京:高等教育出版社, 2007: 119-145.

[17] Cardei M, Thai M T, Ying-shu L, et al.. Energy-efficient target coverage in wireless sensor networks[C]. 24th Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM 2005), Miami 2005:1976-1984.

[18] Sengupta S, Das S, Nasir M D, et al.. Multi-objective node deployment in WSNs: in search of an optimal trade-off among coverage, lifetime, energy consumption, and connectivity[J].Engineering Applications of Artificial Intelligence, 2013,26(1): 405-416.

[19] Kashi S S and Sharifi M. Coverage rate calculation in wireless sensor networks[J]. Computing, 2012, 94(11): 833-856.