基于阻塞预处理的多基地雷达抗主瓣干扰算法

王 强张永顺 司文涛

(空军工程大学防空反导学院 西安 710051)

1 引言

当干扰信号进入雷达天线主瓣时，单(双)基地雷达的检测性能将明显下降。目前常见的干扰抑制方法主要有以下3种：(1)自适应波束形成；(2)天线极化特性；(3)干扰相消。这些方法虽然有一定改善效果，但不同程度会造成主瓣畸变与有用信号被抑制等问题。对此文献[1-4]分别提出了对角加载法、采样协方差矩阵求逆法以及阻塞矩阵预处理法，这些方法解决了主瓣畸变问题，但同时也产生了计算量增大、信噪比降低、性能不稳定等新问题。与此同时，文献[5]中研究了空间有源相关干扰背景下的多基地雷达目标检测性能，论证了在不抑制目标回波的前提下，实现主瓣干扰对消的可行性。然而当各接收站间信号幅度起伏存在相关性时，在空间的某些位置，目标回波依然会同干扰一起被对消掉。

结合以上分析，本文从多基地雷达站间信息联合处理角度出发，提出了不同接收站之间目标回波信号幅度起伏相关时，多基地相参雷达抑制主瓣干扰的新算法。该算法首先构造了阻塞矩阵，并将其引入到直接矩阵求逆中，从而获取自适应信号处理的初始权值，然后依托变遗忘因子递归最小二乘(VFF-RLS)算法的迭代过程，结合高阶累积量的盲高斯特性，实现权值的不断更新。最后通过主瓣干扰对消仿真实验，验证了该方法的有效性，有效解决了目标回波被抑制的问题。

2 幅度起伏相关的目标回波信号模型

假设多基地雷达有n个接收站，当不同接收站之间基线长度满足站间强相关的条件时[5]，结合文献[5-7]可推出第个接收站的目标回波信号为

式中1siB 为第个接收站与参考站的目标回波信号幅度比，1sb为参考站目标回波信号的均方根幅度，其服从均值为，方差为的瑞利分布，为归一化的复包络，sit为信号延迟时间，分别为载波频率与多普勒频移，为参考站目标回波信号的随机初相位，其服从内的均匀分布，为第个接收站关于参考站的相位偏移量。对于参数的估计，需要结合多基地雷达的特点，即目标的运动将产生关于收发站不同的径向速度。本文着重研究T-Rn型多基地雷达，则第 ( 1,i i=2,,)n…个接收站目标回波信号的为[8]

以上是幅度起伏相关的目标回波信号模型，对于干扰信号的模型具体参见文献[5,9]，下面将着重分析提出一种改进的最优检测器。

3 改进最优检测器

关于多基地雷达不同接收站之间，幅度起伏相关目标回波信号的检测，文献[6]中提到了一种两步最优检测器。但是利用该最优检测器检测目标时，在空间的某些位置，目标回波信号会同干扰一起被对消。为了改善这一现象，本文引入了阻塞矩阵对信号进行预处理。阻塞过程采用多级维纳滤波思想，考虑到迭代级数过多，会造成运算量的大幅增加，因此迭代级数设定为3级。以下分析研究假设空中仅有1个主瓣干扰源，且干扰方向已知，干扰类型为窄带。结合实际需要，在此选取2T-R型多基地雷达进行分析研究。改进的检测器结构见图1。

由图1知，改进的最优检测器分两步：第1步进行辅助通道内目标回波信号的阻塞预处理，以及主辅通道的站间信息融合处理；第2步进行两站间数据的加权求和，权值的分配与目标回波信号的空间相干性，以及信号在不同接收站输入端的幅度起伏统计特性有关。图1中，分别表示接收站1，接收站 2的输入端信号，表示不同级的估计偏差，表示不同级的迭代权值，表示前一级匹配输出与观测信号的归一化互相关函数矢量，其表达式为

图1 幅度起伏完全相关信号的改进最优检测器

结合文献[5]提到的幅度起伏相关时，不同接收站的输出 SINR关系式，分析可知，在空间的某些位置之所以会出现目标回波信号被对消，主要是因为该处的目标回波信号与干扰信号在两个接收站输入端的到达时间差相等，同时两接收站间目标回波信号保持同相，这两方面导致目标回波信号具有了类似干扰信号的站间特性。对此问题，通过采用以上阻塞预处理过程，使得阻塞通道输出信号中不包含目标回波信号，可理解为该通道输出的目标回波信号的到达时间趋于无穷大，即使干扰源与目标在空间重合，ijtΔ也不等于0。经过阻塞预处理后，推导得出接收站i的输出信干噪比为

4 基于阻塞预处理的自适应主瓣干扰对消算法

针对文献[5]中提到的AMJCA算法，本文提出了一种基于阻塞预处理的自适应主瓣干扰对消算法(BP-AMJCA)。该算法主要分为两部分：第1部分将阻塞预处理与直接矩阵求逆法相结合，快速得到其初始权向量；在第2部分的权值更新过程中，考虑到高阶累积量具有盲高斯特性，能够克服噪声对算法稳定性的影响[11,12]，因此将高阶累积量引入到变遗忘因子RLS算法[1315]-，得到HOC-VFF-RLS算法。该算法具体如下：

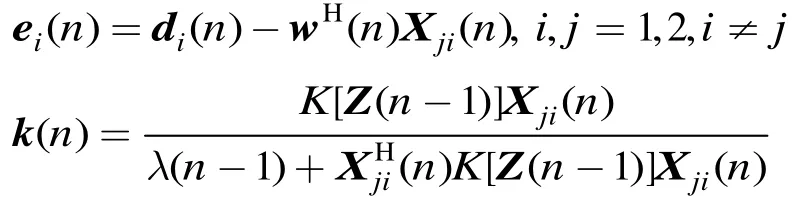
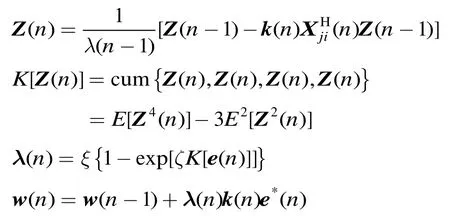
针对以上所提算法，本文主要从算法复杂度与算法性能两方面进行分析。

4.1 算法复杂度分析

衡量算法复杂度可从空间复杂度与时间复杂度两方面进行。本文着重从时间复杂度方面，分析对比传统LMS-AMJCA算法与BP-AMJCA算法的运算量。设定多基地雷达系统为一发两收型，雷达天线主波束内有一个目标源与一个干扰源。两个接收机内部均有M个延迟通道，数据采样点数为N。两种算法运算量的比较情况如表1所示。

表1 不同算法的运算量比较

由表1可知，若从算法运算量分析比较，本文提出的 BP-AMJCA算法的总运算量略大于传统的LMS-AMJCA算法，其中两种算法的矩阵求逆运算量相当，相关矩阵的运算量由上至下增加不大，而且在数据仿真中，计算相关矩阵比矩阵求逆容易。因此，通过对两种算法的时间复杂度分析可知，BPAMJCA算法与传统LMS-AMJCA算法复杂性相差不大，更重要的一点就是 BP-AMJCA算法可以用来解决目标回波信号被对消这一问题。

4.2 算法性能分析

考虑到本文提出的 BP-AMJCA算法由两部分组成，其中第2部分的权值更新过程是影响算法性能的关键所在。鉴于以上分析，在此主要将 HOCVFF-RLS算法与文献[16]中提到的最优 VFF-RLS算法进行对比仿真。仿真实验设置如下：输入信号为，采样点数10000个，自适应滤波器为 3抽头，并设定初始权向量为 0，噪声为加性高斯白噪声，最优 VFF-RLS算法的最小遗忘因子为0.98。仿真结果如图2和图3。

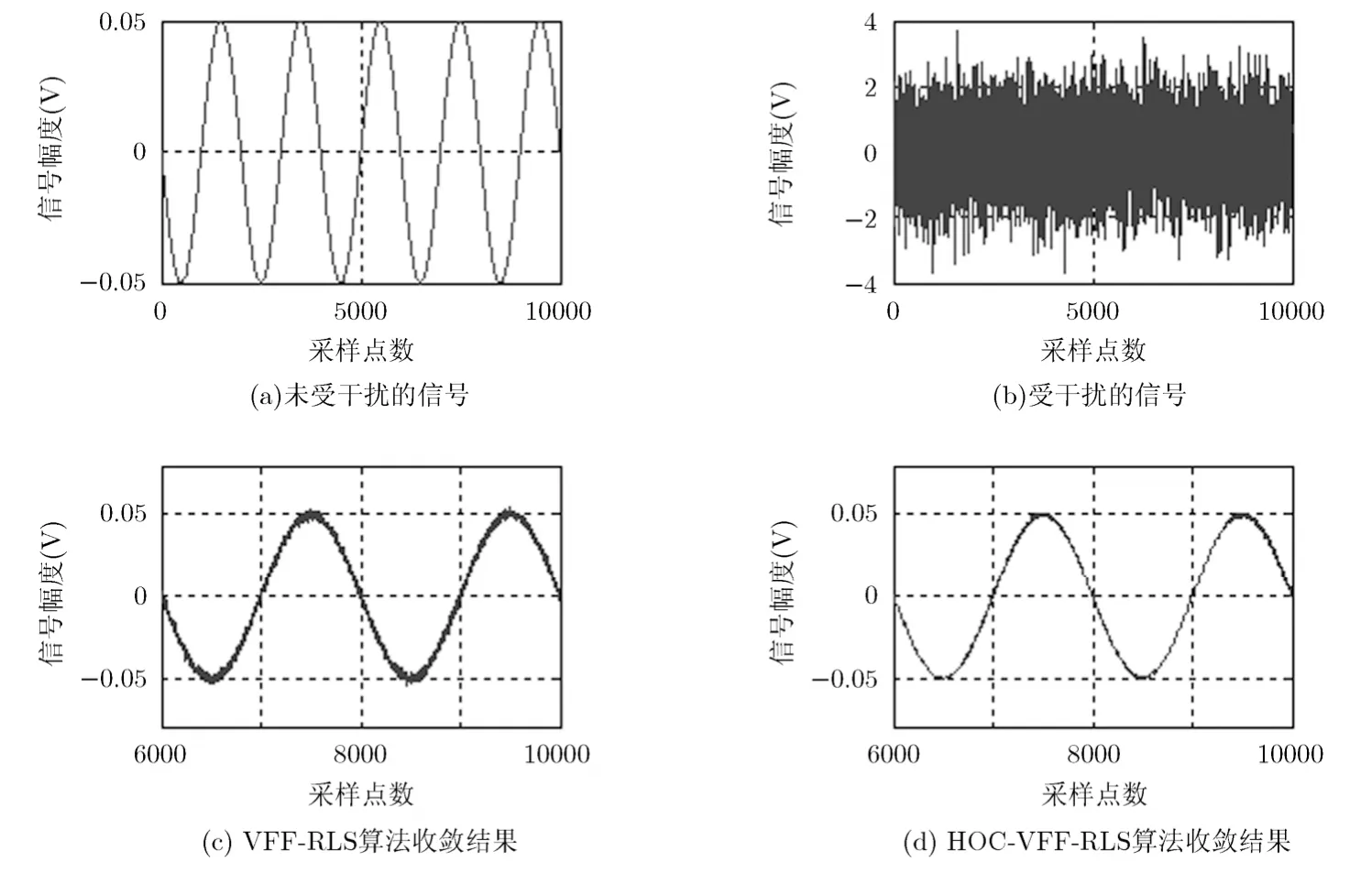
图2 对消前后的输出信号波形

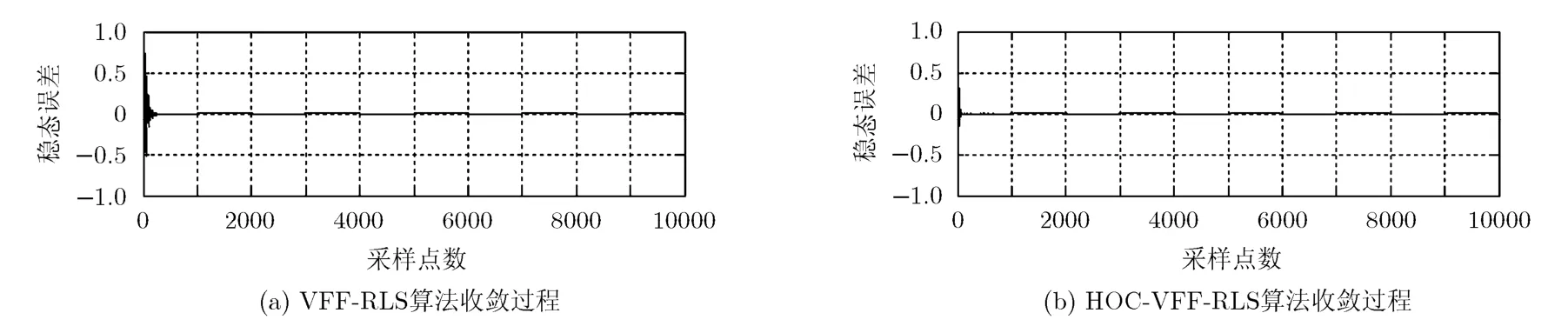
图3 不同算法的收敛速度

由以上两幅图可以看出，HOC-VFF-RLS算法无论从干扰对消效果，还是从算法收敛速度均优于VFF-RLS算法，这与高阶累积量的盲高斯特性有着密切关系。为了进一步分析所提算法在主瓣干扰抑制方面的性能，下面将重点就此进行仿真研究。

5 仿真实验与分析

分析图4，图5，图6，图7的仿真结果，可得以下结论：(1)当目标与干扰机的横向距离等于28.9 m 时，空间存在着目标回波对消点。 (2)仅考虑单个接收站的情况下，若未经过阻塞预处理，本文提出的基于HOC-VFF-RLS改进的AMJCA算法比传统LMS-AMJCA算法的输出SINR有8~10 dB的改善，这与高阶累积量的盲高斯特性有很大关系。而加入阻塞预处理后，有效解决了目标回波被对消的问题，并且本文提出的 BP-AMJCA算法使得输出SINR改善量为25~30 dB。(3)考虑到以上处理是在牺牲辅助通道目标回波信号的前提下进行的，因此将两个接收站的输出做加权求和，输出 SINR改善量将提升为35~40 dB。(4)图7关于目标回波对消点处SINR的改善，更进一步体现了本文提出的基于 HOC-VFF-RLS改进的 AMJCA算法和BP-AMJCA算法的抗干扰性能。

6 结束语

图4 单个接收站时，未加阻塞的算法比较

图5 单个接收站时，加入阻塞的算法比较

图6 两个接收站时，加入阻塞的算法比较

图7 目标回波对消点处，不同算法的比较

针对多基地雷达不同接收站之间信号幅度起伏相关时，在空间的某些位置，目标回波信号同干扰一起被对消这一现象，本文首先建立了幅度起伏相关的目标回波信号模型，给出了多基地雷达目标回波信号TOA、多普勒频率的定量计算公式，然后通过引入阻塞预处理，对幅度起伏相关的目标回波信号检测器做出改进，解决了目标回波信号被抑制的问题。最后在对消仿真中，通过提出 BP-AMJCA算法与HOC-VFF-RLS算法，有效改善了主瓣干扰背景下，多基地雷达的输出SINR。仿真结果表明了该方法的有效性与可行性。

[1] Vorobyov S A, Gershman A B, and Luo Z Q. Robust adaptive beamforming using worst-case performance optimization: a solution to the signal mismatch problem[J]. IEEE Transactions on Signal Processing, 2003, 51(2): 313-324.

[2] Chang L and Yeh C C. Performance of DMI and eigenspacebased beamformers[J]. IEEE Transactions on Antenna Propagation, 1992, 40(11): 1336-1347.

[3] 刘柏君. 高频雷达中基于多频信号的波束形成方法研究[D].[硕士论文], 哈尔滨工业大学, 2011.

[4] 刘聪锋, 杨洁, 甘昶. 加载与约束结合的主瓣干扰抑制方向图保形[J]. 电波科学学报, 2012, 27(2): 344-349.

[5] Chernyak V S, Zhou Wan-xing, Wu Ming-ya, et al..Fundamentals of Multistatic Radar Systems: Multistatic Radars and Multiradar Systems[M]. Beijing: Publishing House of Electronics Industry, 2011: 177-189.

[6] 葛先军, 张财生, 宋杰, 等. 无源双基地雷达随机初相补偿及误差影响分析[J]. 系统工程与电子技术, 2012, 34(10):2023-2027.

[7] Niu Zhi-jun and Pei Bing-nan. Study on suppression of main-lobe interference in over the horizon radar[C]. 2012 IEEE International Conference on Information Science and Technology, Wuhan, 2012: 410-413.

[8] 刘红明. 双基地 MIMO雷达原理与理论研究[D]. [博士论文],电子科技大学, 2011.

[9] Kong Ling-jiang, Yang Mei, and Zhao Bin. Adaptive detection for shared-spectrum multistatic radar in Gaussian clutter[C]. 2012 IEEE Radar Conference, Atlanta, 2012:309-313.

[10] 黄庆东. 最小模级联相消器算法研究[D]. [博士论文], 西安电子科技大学, 2011.

[11] 李晶晶. 基于新型变步长LMS的自适应谐波检测算法[D]. [硕士论文], 南京信息工程大学, 2012.

[12] Kapil Belpatre and Mrs Bavhute M R. Comparative performance study between the time-varying LMS (TVLMS)algorithm, LMS algorithm and RLS algorithm[C]. National Conference on Innovative Paradigms in Engineering ＆amp;Technology, USA, 2012: 6-10.

[13] Cai Zhan-hui and Yao Yuan-cheng. Automatic modulation identification of MPSK signals using differential signal and its high order cumulants[C]. 2011 7th International Conference on MEMS, NANO and Smart Systems, Malaysia, 2011: 2547-2551.

[14] Xu Yan-yun, Dai Shun, Wu Shi-you, et al.. Vital sign detection method based on multiple high order cumulant for ultrawideband radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(4): 1254-1265.

[15] Marei M I, El-Saadany E F, and Salama M M A.A flexible DG interface based on a new RLS algorithm for power quality improvement[J]. IEEE Systems Journal, 2012,6(1): 68-75.

[16] 邵亚勇, 竺小松. RLS算法及其改进形式在信号分离中的应用分析[J]. 电子测试, 2012, (1): 23-27.