细节疲劳额定强度形状参数取值

郭 翔， 刘建中， 胡本润， 黄 啸

(北京航空材料研究院 航空材料检测与评价北京市重点实验室，北京100095)

细节疲劳额定强度DFR(detail fatigue rating)是波音公司提出的一种飞机设计方法［1］。其中形状参数α 是确定DFR 值的关键参数。波音公司［2，3］于20 世纪60，70年代收集了包括2000 多组铝合金试件，1200 多组钛合金试件和800 多组钢结构试件的疲劳寿命数据，给出了不同材料的α值:α=4 适用于铝合金结构;α =3，适用于钛合金结构和抗拉强度小于1655MPa 的钢结构;α =2.2适用于所有抗拉强度高于1655MPa 的钢结构。目前，我国的飞机设计手册［4，5］仍 直接采 用这一结果。

周希沅［6］通过极大似然估计法对多种国产材料的α 值进行了初步估计，并与美国同种材料的α值进行了比较，给出了国产材料α 值的变化范围。黄啸等［7］分析研究周希沅初步计算的α 值在其范围内变化对DFR 值的影响。但是，由于文献［6］与波音公司采用的估计方法不同，且数据样本量过小，其估计结果的可靠性有待进一步论证。

波音公司计算α 估计值时采用了国内外统计学文献中非常少见的头两序数估计法。该方法与极大似然估计法、矩估计法等常用的参数估计法的合理性研究未见报道。同时，国产材料与国外材料在冶金质量、工艺稳定性及试件制造水平等方面均有较大差别，这些差别都可能显著影响疲劳寿命分散性，进而影响α 取值。在使用国产材料的飞机设计中，直接采用波音公司针对美国生产材料获得的α值是否合理，这需要通过收集大量可靠的国产材料与结构疲劳试验数据，采用与波音公司相同的α 值估计方法进行深入研究与系统验证。另外，经过几十年材料科学的发展，新材料例如第三代铝锂合金、纤维金属层板等，正逐步应用于先进飞机结构，其α取值如何，国内外均未见相关报道，也急需进行研究，为飞机设计者提供参考。

本工作介绍波音公司所采用的头两序数估计法，以及通过此估计方法得到一类材料α 值的过程。对头两序数估计法和其他常用的参数估计方法进行优劣性评价。采用头两序数估计法分析国内常用航空材料疲劳寿命数据，与美国相同材料数据对比。对铝锂合金，纤维金属层板等新型航空材料的α 值进行计算。

1 形状参数α 的估计方法

参数估计是根据从总体中抽取的样本估计总体分布中包含的未知参数的方法。统计理论中对于Weibull 分布常用的参数估计方法有极大似然估计法，最小二乘估计法和矩估计法等［8～10］。然而，Whittaker 在为波音公司制定美国材料α 值时所采用的参数估计方法是不常见的头两序数估计法。

1.1 头两序数估计法

将相同试样在相同试验条件下的全体疲劳寿命视作总体，那么，一个样本容量为n 的样本则应是实验室中相同条件下测试同一批n个试样得到的n个疲劳寿命。

在DFR 方法中，疲劳寿命的分布以两参数Weibull 分布描述，其分布函数为:

式中:N ＞0，α ＞0，β ＞0;α 为形状参数;β 为尺度参数;N 为疲劳寿命。

为获得形状参数α 值，头两序数估计法在进行严格的推导后，得到总体的α 值估计量为

式中:n 为样本量;x(k)为样本顺序统计量(k =1，2，…，n)。

同时，如果多个样本来自α 值相同的总体，那么这些样本通过式(2)得到的多个满足理论分布:

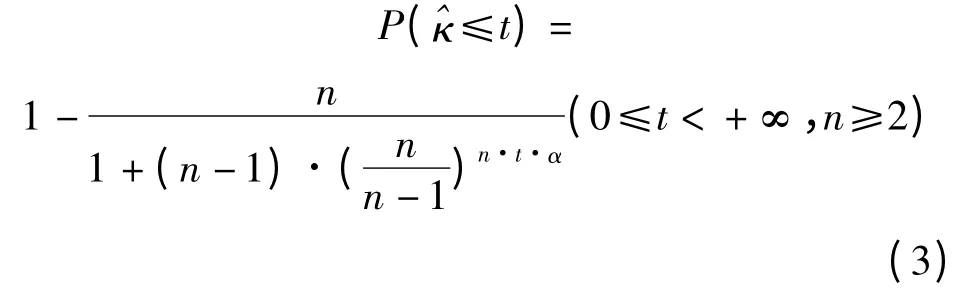
疲劳寿命数据样本存在x(1)=x(2)的情况，此时通过式(2)得到，这使得对数据做进一步处理，如取平均值，变得十分困难。为了解决这一问题，采取与波音公司相同的方法［2］，对计算出的先取倒数，再对进一步处理，如求平均值、做经验累计分布曲线等，待得到最终的κ 值后，再取倒数α=1/κ 得到α 值。

对于一种材料，如铝合金，波音公司确定其工程α 值的过程有以下4 步:

1)收集铝合金材料或结构的疲劳寿命数据。试验或服役条件完全相同的疲劳寿命数据为一个样本，且样本量不小于2。由式(2)得到每一个样本的。

2)假设所有样本所在的总体具有同一个α 值，并对此进行假设检验。如检验各牌号下样本的α值是否相同，则将上一步得到的α 估计值按牌号分为若干组，做出每一组α 估计值倒数κ 的经验累积分布曲线，若这些曲线间的相似程度满足一定要求，则认为牌号对α 值无显著影响，反之则存在影响。

3)依次检验所关注的因素。结果显示，美国铝合金材料的牌号、几何形状、服役温度、试验机、加载形式和疲劳寿命(102～106范围内)等因素对α 值的影响不显著。

4)做出铝合金所有样本κ 值的经验累积分布曲线，并通过式(3)进行拟合，拟合度满足一定要求时，式(3)中的参数α 即为铝合金的α 值。文献［2］中采用Mann 的算法得到全体铝合金数据的加权平均值=0.224，再通过切比雪夫不等式得到一个满足概率P(κ ＜κ'0.95)＞95%的κ 值:κ'0.95=0.25(α=4)，并认为这一值在满足拟合度的情况下更为保守，适合作为工程参考的α 值。

由于头两序数估计法并不常见，为保证统计分析的正确，根据文献［2，3］中的原始数据对美国材料的α 值进行了再次估计，并和文献中采用上述步骤给出的计算结果进行对比。该文献为国外早期报告，在印制和保存过程中，其附录中的部分数据丢失，仅对能够掌握的数据进行验证，这会造成一些误差。查得的铝合金数据1966个，这些均由头两序数估计法得到，平均值为0.261，文献［2］中给出的统计结果中共有2003个，平均值为0.259，二者误差为0.77%。通过头两序数估计法得到的钛合金和钢材数据的验证结果和其文献［3］给出的结果列于表1，表2 中。

对比结果显示，在头两序数估计法下，钛合金得到的验证数据，与文献中数据的误差在5. 04%以内，钢材的误差在11.07%以内。

以上验证结果说明，采用上述头两序数估计法得到α 值的计算方法与文献通过原始数据得到α值所采用的计算方法一致。

表2 钢材κ 估计值对比Table 2 κ estimators' verification for steel

1.2 不同估计方法的评价

为了研究头两序数估计法的合理性，分析头两序数估计法与其他常用估计方法的差异，利用包括头两序数估计和极大似然估计在内的五种常用估计方法对母体分布已知的随机模拟数据进行估计，通过估计的期望和方差评价其优劣性。

具体的方法为，通过Matlab 软件随机产生符合双参数Weibull 分布的模拟疲劳寿命数据样本，样本量分别为2，3，4，5，10 和20，每个样本量下生成5000个样本，设定Weibull 分布参数为(κ，β)=(0.25，10000)。模拟生成的样本通过不同估计方法对κ 进行估计，每一种估计法都可以得到一系列估计值。通过期望和方差表征估计量的优劣:

在估计Weibull 分布的形状参数时，极大似然估计量和矩估计量均通过统计学中常见的方法得到［11，12］。在相关文献［13，14］中已有结果表明加权最小二乘法较传统最小二乘法更有优势，通过计算发现Lu［14］的加权因子更优，因此只列出Lu 给出的加权最小二乘法结果。图1 给出了在不同样本量n下，各估计方法由式(4)得到期望值与设定值0.25之间的误差值;图2 则给出了各估计方法由式(5)得到的方差。

图1 不同估计方法期望的比较Fig.1 Expectation comparison among estimators

图2 不同估计方法方差的比较Fig.2 Variance comparison among estimators

由图1 可知，通过头两序数估计法得到的期望值与真实值的偏差小于其他估计方法，这在小样本量情况下尤为明显，可认为头两序数估计法在估计的准确度上优于其他估计方法。由图2 可知，头两序数估计法的方差大于其他估计方法，但是，最终α值并非由单个样本估计，而是由大量样本的估计值取平均值得到。因此，针对估计α 值，评价的估计方法时，方差为次要因素。此外，受试验时间和经济成本的影响，高周疲劳寿命数据以小样本为主［15］，在已掌握的国内外疲劳寿命数据中，国外数据样本量n ＜5 的样本占总样本数的96.5%，国内数据则占82.2%。在此情况下，头两序数估计法虽然不能认为是统计学上的最优估计，但综合以上几点，在估计α 值时头两序数估计法是最合适的估计方法。

2 国产飞机材料α 值的统计分析

2.1 常用飞机材料

对于国产材料与结构，其α 值是否可直接采用国外相同材料的α 值需进一步验证，本工作统计分析了北京航空材料研究院产生的1060 组国产铝合金，505 组国产钛合金和658 组国产钢材的实测数据，利用头两序数估计法对这三类材料的α 值进行估计。

为确定牌号、Kt值、试件几何形状及试验环境等因素对α 值的影响，对可能影响α 值的因素，进行置信度为95%的显著性分析，显著性分析采用单因素方差分析，以确定某一因素中的不同水平对α值是否有影响。例如，对Kt值的影响进行方差分析。选取除Kt值外，其余条件完全相同的疲劳寿命数据共n个样本，此时设Kt值有s个水平，Kt=1，Kt=2，…Kt=s，每一水平下有若干个，记为每个水平下^α 的均值，则待检验的假设为:

给定显著性水平γ，根据方差分析的理论计算其F 值，当F ＞F1-γ(s-1，n-s)时拒绝原假设H0，否则认为分析结果与原假设H0无显著差异，即由不同Kt值样本所估计出的α 值无明显差异。依次以此方法分析可能影响α 值的其余因素。表3 给出分析结果，有显著影响以“+”表示，反之以“－”表示。

表3 各因素对不同材料形状参数的影响Table 3 The effect of different factor on different materials

由表可见，中值寿命范围对所有材料的α 值都有显著影响，抗拉强度仅对钢材的α 值有显著性影响，试验腐蚀环境对牌号为30CrMnSiNi2A 和16Co14Ni10Cr2Mo 的钢材有显著性影响。其余因素:Kt值、试件几何形状及试验温度则对材料的α值无显著影响。在此基础上，研究国产铝合金和钛合金的α 值，只需关注α 值在不同中值寿命范围内的取值。

表4 分别给出国产铝合金和钛合金在不同寿命范围内的α 值。

表4 国产铝合金形状参数估计结果Table 4 Estimated shape parameters of aluminum alloy

根据表3 中的结论，研究国产钢材的α 值，除中值寿命范围外，还应关注材料的抗拉强度及个别材料在腐蚀试验环境下的 α 值。表6 给出了30CrMnSiNi2A 和16Co14Ni10Cr2Mo 寿命范围在6 ×104～2×105下不同腐蚀环境的α 值。表7 则给出了不同抗拉强度下钢材的α 值以及不同寿命范围下的α 值，其中30CrMnSiNi2A 和16Co14Ni10Cr2Mo 两类材料不包含腐蚀环境下的数据。

表5 国产钛合金形状参数估计结果Table 5 Estimated shape parameters of titanium alloy

表6 腐蚀环境对30CrMnSiNi2A 和16Co14Ni10Cr2Mo形状参数影响Table 6 Estimated shape parameters of 30CrMnSiNi2A and 16Co14Ni10Cr2Mo in different corrosion environment

通过以上计算与分析发现，国产材料的α 值随中值寿命的增加有减小的趋势，30CrMnSiNi2A 和16Co14Ni10Cr2Mo 两种钢材在不同的腐蚀试验环境下得到的α 值有明显不同。从表7 可见随抗拉强度σb的增加，钢材的α 值有减小的趋势，以σb=1655MPa 为界将钢材分为两类，这两类钢材的α 值有明显区别，这与文献［2，3］中得到的结论一致。

2.2 新型飞机材料

铝锂合金较铝合金比重低，刚度大，同时保持较高的强度、较好的抗腐蚀性和抗疲劳性。纤维金属层板是由铝合金和玻璃纤维或碳纤维增强复合材料组成的一种混杂结构材料，具有优异的损伤容限性能［16］。这两类新材料在国外新型飞机上已有实际应用，为了在国内飞机设计时提供这两类材料的DFR 值，对铝锂合金的α 值进行估计，分析了8 种铝锂合金243 组1024个试样。

对可能影响铝锂合金α 值的因素进行了单因素方差分析。中值寿命范围对α 值有较大影响，除此之外材料的牌号、试件形状、Kt值和试件所用材料的取样方向等因素，在置信度95%的检验下未发现明显影响铝锂合金α 值的因素。

表8 给出了全体铝锂合金在不同寿命区间内的α 值。表9 则给出了2 × × ×系列铝合金与2 × ××系列铝锂合金寿命范围在6 ×104～2 ×105内的α值。

表8 铝锂合金形状参数估计结果Table 8 Estimated shape parameters of aluminum lithium alloy

表9 2 × × ×系列铝锂合金与2 × × ×系列铝合金形状参数估计结果对比Table 9 Estimated shape parameters of aluminum lithium alloy(2× × × series)and aluminum alloy(2× × × series)

通过表4 和表8 的对比以及表9 中相同系列铝合金与铝锂合金α 值的估计结果对比可以观察到，铝锂合金的α 值略大于铝合金的α 值，这表明铝锂合金的疲劳寿命分散性略小于铝合金。

根据两类新型纤维金属层板共19 组53个试样的疲劳寿命数据，对层板的α 值进行初步分析，表10 给出了两类铝合金层板的α 值，其中铝合金-碳纤维层板8 组，铝合金-玻璃纤维层板11 组。

表10 新型铝合金纤维金属层板形状参数估计结果Table 10 Results of shape parameters of fiber metal laminates

由初步估计的结果可以看出，两类新型纤维金属层板之间的α 值存在差异。目前收集到的数据还不足以判断不同类型纤维金属层板是否可以使用同一个α 值，对于纤维金属层板α 取值还需要大量的疲劳寿命试验数据。

3 国产材料α 值取值分析与建议

根据以上分析与计算，将疲劳寿命范围在6 ×104～2 ×105循环下的国产铝合金、钛合金、钢材和铝锂合金的α 值和已有文献中所统计的α 值列入表11，其中σb≤1655 MPa 钢材在腐蚀环境下的数据不包含两类对腐蚀试验环境敏感材料30CrMnSiNi2A 和16Co14Ni10Cr2Mo。

表11 国内外材料疲劳寿命形状参数对比Table 11 Comparison between Domestic material's α and American's

表11 结果显示，国产航空材料的α 值随材料种类的变化趋势与美国材料基本一致。同时，国产材料的α 值均大于美国材料，这一结果说明，国产材料的疲劳寿命分散性较美国材料小。然而，从大量实测结果及服役数据来看，国产材料与美国材料相比稳定性较差，表11 中得到的结果似乎并不符合实际经验。这是由于评估的国产材料数据均来自材料级别的试验，并且这些试验都在过程与环境可控实验室条件下进行，而美国用于估计的材料数据还包含了大量结构模拟件试验数据及服役数据。

在获取更多模拟结构试件和服役数据等多来源数据前，对于国产材料，铝锂合金可参考铝合金的α值选取，其余材料仍直接采用手册中的α 值。对于纤维金属层板的α 值，相关试验数据较少，只做初步分析。待试验数据更为充分后，可依照以上分析方法对手册中给出的各类材料的α 值进行相应调整，并给出层板等新型航空材料的α 值。

4 结论

(1)头两序数估计法计算α 值，估计准确性高，误差不超过5%，更适合小样本的估计等特点。

(2)利用两序数估计法对国产材料评估可知，寿命取值范围对国产航空材料的α 值影响明显，抗拉强度对钢材的α 值影响明显，腐蚀环境对个别牌号钢材的α 值影响显著。Kt值，试件几何形状及试验温度对α 值无显著影响，α 的最终估计值及不同材料间的变化趋势与美国材料基本相同。

(3)在获得更多更全面的数据前，铝锂合金的α值按照手册中铝合金的α 值选取，其余材料仍直接采用手册中的α 值。

［1］GORANSON G. Elements of structural integrity assurance［J］. Fatigue，1994，16(1):43 －65.

［2］WHIITTAKER I C，BESUNER P M. A Reliability Analysis Approach to Fatigue Life of Aircraft Structures［R］. AD 853263，1969.

［3］WHIITTAKER I C. Development of Titanium and Steel Fatigue Variability Model for Application of Reliability Analysis Approach to Aircraft Structures［R］. AD758219，1972.

［4］吴学仁. 飞机结构金属材料力学性能手册［M］. 北京:航空工业出版社，1996.

［5］郑晓玲. 民机结构耐久性与损伤容限设计手册［M］. 北京:航空工业出版社，2003.

［6］周希沅. 国产材料疲劳寿命分布参数α 的初步估计［J］. 航空学报，1990，11(10):488 －491.(ZHOU X Y. Preliminary estimation of the shape parameters of fatigue life distribution for domestic materials［J］.Acta Aeronautica et Astronautica Sinica，1990，11(10):488 －491. )

［7］黄啸，刘建中，马少俊，等. 细节疲劳额定强度计算参量取值敏感性研究［J］. 航空学报，2012，33(5):863－870.(HUANG X，LIU J Z，MA S J，et al. Sensitivity analysis of the parameters in detail fatigue rating equation［J］. Acta Aeronautica et Astronautica Sinica，2012，33(5):863 －870.)

［8］MANN N R. Tables for obtaining the best linear invariant estimates of parameters of the Weibull distribution［J］.1967，9(4):629 －645.

［9］NELSON W. Applied Life Data Analysis［M］. New York:John Wiley ＆ Sons，1982.

［10］NELSON W. Accelerated Testing:Statistical Models，Test Plans，and Data Analysis［M］. New York:John Wiley ＆Sons，1990.

［11］陈家鼎，孙山泽，李东风，等. 数理统计学讲义［M］. 第二版. 北京:高等教育出版社，2006:17 －19.

［12］金良琼. 双参数Weibull 分布的参数估计［D］. 昆明:云南大学，2010.

［13］HUNG W L. Short communication weighted least-squares estimation of the shape parameter of the Weibull distribution［J］. 2001，17(6):467 －469.

［14］LU H L，CHEN C H，WU J W. A note on weight leastsquares estimation of the shape parameter of the Weibull distribution［J］. 2004，20(6):579 －586.

［15］崔卫民，薛红军，喻天翔，等. 试验数据服从Weibul1分布时可靠性试验最少试件数的确定术［J］. 机械工程学报，2008，44(1):51 －55.(CUI W M，XUE H J，YU T X，et al. Determination of sample size for weibull distribution in structural reliability tests ［J］. Chinese Journal of Mechanical Engineering，2008，44(1):51 －55.)

［16］黄啸，刘建中. 新型纤维金属混合层板结构的疲劳裂纹扩展与分层行为［J］. 航空材料学报，2012，32(5):97 －102.(HUANG X，LIU J Z. Fatigue crack propagation and delamination behavior of advanced fiber metal hybrid laminate［J］. Journal of Aeronautical Materials，2012，32(5):97－102.)