基于三次均匀B样条的卡通形象设计技术*

丁永胜 ，李朝红 ，祝 微

（1.齐齐哈尔大学 理学院 数学系，黑龙江 齐齐哈尔 161006；2.齐齐哈尔高等师范专科学校 数学系，黑龙江 齐齐哈尔 161005）

1 基本知识

已知 n+1 个控制顶点 Pi（i=0，1，…，n），则 p 次（即p+1阶）B样条曲线的表达式为：

其中，Ni，p（u）是调和函数，即为 B 样条基函数。 Schoenberg[1]给出定义：给定参数轴U上的一个分割，由下列递推关系定义的称为U的p次（阶）B样条基函数：

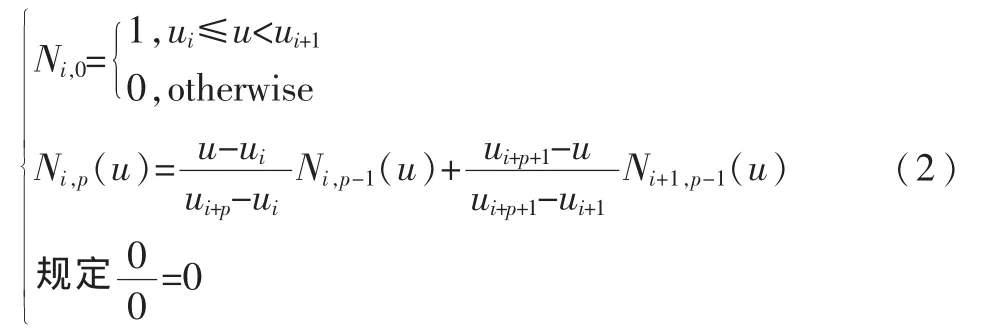
其中，p 表示 B 样条的次数（即 p+1 阶），U={u0，u1，…，un+p+1}为节点矢量，ui为节点。当节点沿参数轴均匀等距分布，即ui+1-ui为常数时，则表示均匀B样条；反之，ui+1-ui不为常数时，则表示非均匀B样条。利用式（1）可以得到三次均匀B样条基函数：

通过B样条基函数可以很容易得到B样条曲线的性质[1-3]。

（1）严格的凸包性。曲线严格位于控制多边的凸包内。

（2）局部性。对于 k（即 p+1）阶 B样条曲线上参数为 t∈[ti，ti+1]的点 P（t），至多与 k 个控制顶点 Pj（j=i-k+1，…，i）有关，与其他控制顶点无关；移动该曲线的第 i个控制顶点Pi至多影响到定义在区间（ti，ti+k）上那部分曲线的形状，对曲线的其余部分不产生影响。

（3）可微与连续性。在定义域内重复度为k的节点处则使p-k次可微或具有p-k阶参数连续性。

（4）分段参数多项式。 C（u）在每一区间 u∈[ui，ui+1）上都是次数不高于p的多项式。

（5）近似性。控制多边形是B样条曲线的线性近似，若进行节点插入或升阶会更加近似。次数越低，B样条曲线越逼近控制顶点。

（6）几何不变性。B样条曲线的形状和位置与坐标系的选择无关。

基于B样条的优良性质，其造型的功能也十分灵活，用B样条曲线可以构造直线段、尖点、拐点、节点以及切线等特殊情况。

2 控制三次均匀B样条曲线几何形态方法

在设计一般的卡通形象时，常常借助控制三次B样条曲线几何形态使构造的形象更生动，控制三次均匀B样条曲线几何形态主要考虑以下方法技术：

（1）为在曲线内嵌入一段直线，应用4个顶点共线，如图1所示。

（2）为使曲线和特征多边形相切，应用 3顶点共线或二重角点的技术。如果3个连续的控制点共线连成一段直线，则曲线将过直线上的一点，且在此点处，曲线直线化。可以用这样的点构成曲线的拐点，如图2～图4所示。

（3）为使曲线在某一顶点处形成尖点，可在该处使3个顶点相重合，如图5所示。

（4）改变一个顶点，将影响相邻4段曲线的形状，利用B样条曲线的局部性，可以对造型细节进行微调，而不影响全局形状，如图6所示。

（5）用三重顶点或二重顶点控制曲线的端点：用三重顶点时，曲线通过端点，但开始段B样条曲线是一小段直线；用二重顶点时，曲线不通过端点，而在多边形首边上靠近二重顶点的某一点开始。因此，利用控制多边形的多重顶点可以调节曲线的端点位置，以达到形象设计的各种要求。如起点和终点处3点相重，曲线过控制多边形端点，从而具有Bezier曲线的性质，如图7所示；也可以利用重点绘制封闭的三次B样条曲线，如图8所示。

图1 4顶点共线

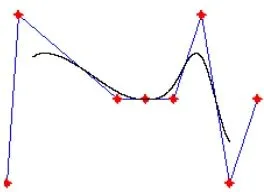
图2 3顶点共线

图3 二重角点

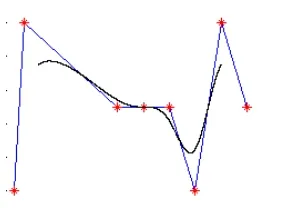
图4 3点共线构造拐点

图5 3点重合构造尖点

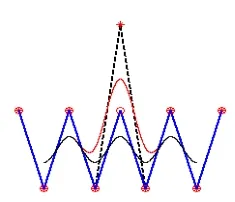
图6 曲线的局部微调

图7 3点重合过控制顶点

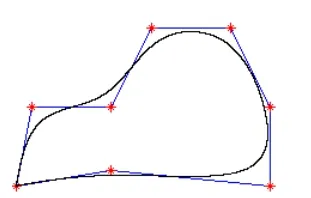
图8 封闭样条曲线

3 基于三次均匀B样条的卡通形象设计

在充分掌握控制三次均匀B样条曲线几何形态之后，可以对二维卡通形象进行设计。首先绘制卡通形象；然后在其上选择采样点构造控制多边形；利用所构造的控制多边形绘制三次均匀B样条曲线；观察卡通的轮廓特点，利用控制三次均匀B样条曲线几何形态方法技术绘制特殊的轮廓曲线特征；最后反复修改，调节形状使其更逼真形象。

如绘制图9中两个企鹅的卡通形象，其采样点如图10所示，其采样点分别设计为以下几类控制多边形矩阵（如图11所示）：大小企鹅翅膀①、大小企鹅外形轮廓线②、大小企鹅眼睛线③、大小企鹅嘴空隙线④、大小企鹅脖线⑤和地面修饰线⑥等。

在构造各类曲线形状时分别用到了曲线内嵌入一段直线、曲线和特征多边形相切、在某一顶点处形成尖点、构成曲线的拐点、利用重点绘制封闭的三次B样条曲线以及曲线过控制多边形端点等各类技巧。

图12给出了海豚卡通形象的采样点数据，图13为海豚的控制多边形，图14为绘制的海豚形象。

图9 企鹅卡通形象

图10 企鹅采样点

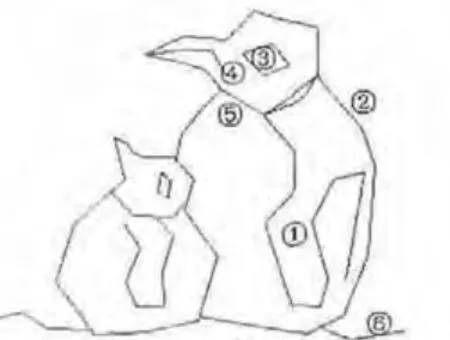
图11 控制多边形

图12 海豚采样点

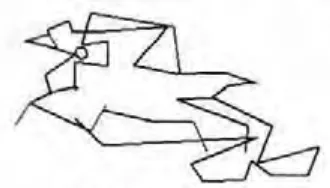
图13 控制多边形

图14 海豚

在设计平面卡通形象时，借助B样条曲线的优良性质控制几何形态，使构造的卡通更形象生动且易修改。因此，只要充分理解、掌握和控制B样条曲线的方法技术，就可以根据不同的需求设计出各类卡通形象；通过进一步修改某处控制顶点，可以使卡通形象发生局部变化，从而达到动态的效果。

[1]施法中.计算机辅助几何设计与非均匀有理B样条[M].北京：高等教育出版社，2001.

[2]张义宽.计算机图形学[M].西安：西安电子科技大学出版社，2005.

[3]张彩明.计算机图形学[M].北京：科学出版社，2005.