优化的 GM(1，1)模型在建筑业总产值预测中的应用

刁 鹏

(江苏国兴建设项目管理有限公司，江苏泰兴 225400)

0 引言

建筑业总产值是指建筑业在一定时期内完成的以价值表现的生产总量。作为国民经济系统的重要组成部分，是在工业化、城市化和现代化发展过程中形成的独立产业。从经济发达的国家或地区来看，建筑产业无一不是该国或地区的先导产业与支柱产业，对当地经济发展起着举足轻重的作用。从我国的情况来看，中国建筑业很大程度解决了就业问题，同时建筑产业的发展同样有效地拉动了经济增长。科学、准确、及时地预测建筑业总产值，对国家制定经济建设计划有着至关重要的影响。

GM(1，1)是最常用的灰色预测模型，由于所需样本数据少、计算方便简单，因而在“小样本、贫信息”的不确定性系统中得到广泛应用。影响建筑业总产值的因素十分复杂，大致可分为外部因素和内部因素，其中外部因素主要有宏观经济环境、固定资产投资等，而内部因素主要包括生产要素、科学技术的进步程度、产业政策等［1］。因此，建筑业体系属于灰色系统，可以用GM(1，1)模型进行预测。

文献［2］～［4］采用函数变换的方法，提高了原始数据的光滑度，从而提高GM(1，1)模型的预测精度。文献［5］提出用二次插值构造模型中的背景值，并用改进的方法进行了短期预测。这些文献都是采用单一的方法，采用函数变换改变原始数据或采用插值法改变背景值。

本文将两种方法结合在一起，首先使用正弦函数变换改变原始数据，再利用二次插值法改造模型中的背景值。并使用优化的GM(1，1)模型对2003年～2012年建筑业总产值进行实证研究，验证了该模型的高精度性和实用性。

1 基于Lagrange插值法的背景值计算

传统的GM(1，1)模型对应的白化微分方程为:

将上式在区间［k，k+1］上积分得:

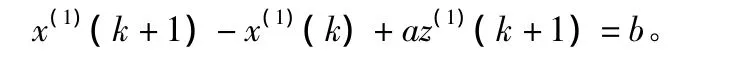
其中，a，b均为待识别常数。

但在传统GM(1，1)模型中，采用紧邻均值处理的背景值为:

也就是说，传统的GM(1，1)模型，在确定待识别常数a和b时，利用梯形面积来近似曲边梯形的面积。所以传统背景值的构造会使a和b偏离正常数，导致模型预测精度降低。

以k，k+1，k+2三个点作为插值节点，则x(1)(t)的二次Lagrange插值多项式pk(t)为:

其中，k=1，2，…，n －2。

我们以pk(t)在［k，k+1］上的定积分作为背景值z(1)(k+1)。由于pk(t)是二次多项式，而计算定积分的Simpson公式具有三次代数精度，故由Simpson公式得到新的背景值［6］:

其中，k=1，2，…，n －2。

2 基于正弦函数和Lagrange插值法的GM(1，1)模型

文献［7］已经证明正弦函数变换能提高原始数据序列的光滑度，从而提高了预测的精度。假设奇异点经过处理后得到的原始数据序列:A(0)={a(0)(k)|k=1，2，…，n}为递增序列，且a(0)(k)＞0。

基于正弦函数以及Lagrange插值法的GM(1，1)建模过程如下:

1)对原始值做相应的数据转化，使其处于单调递减且取值非负的区间，得到新数列:

2)对数列X(0)进行y(0)(k)=sinx(0)(k)函数变换，得到数据序列:

3)对数据序列 Y(0)={y(0)(1)|k=1，2，…，n}作一次累加生成:

4)利用插值法构造背景值得:

其中，

5)由一阶累加生成序列Y(1)建立GM(1，1)模型，对应的白化微分方程为:

6)在初始条件y(1)(1)=y(0)(1)，上述方程的离散解为:

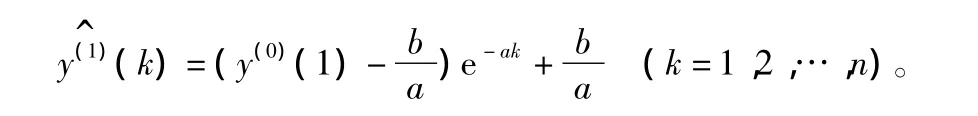
参数列β=(a，b)T由最小二乘法确定:

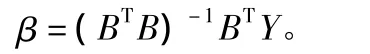
7)将k=1，2，…，n代入上式，便得到 Y(1)的模拟值:

8)还原求出Y(0)的模拟值。由1)得:

10)再经过相应的数据转化还原就可得到原始数据的模拟值:

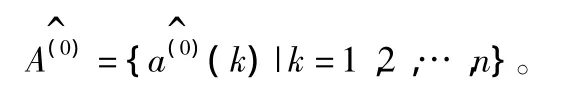
3 实例应用

现利用优化的 GM(1，1)模型对经过处理后数据 A(0)={a(0)(k)|k=1，2，…，10}进行建模。

GM(1，1)模型的时间响应序列为:

最终模型为:

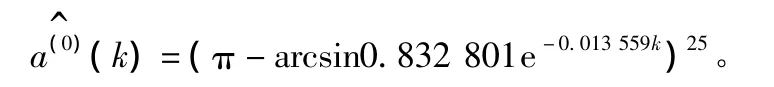
表1为建筑业总产值实际值与预测值对比。

1)后验差检验。

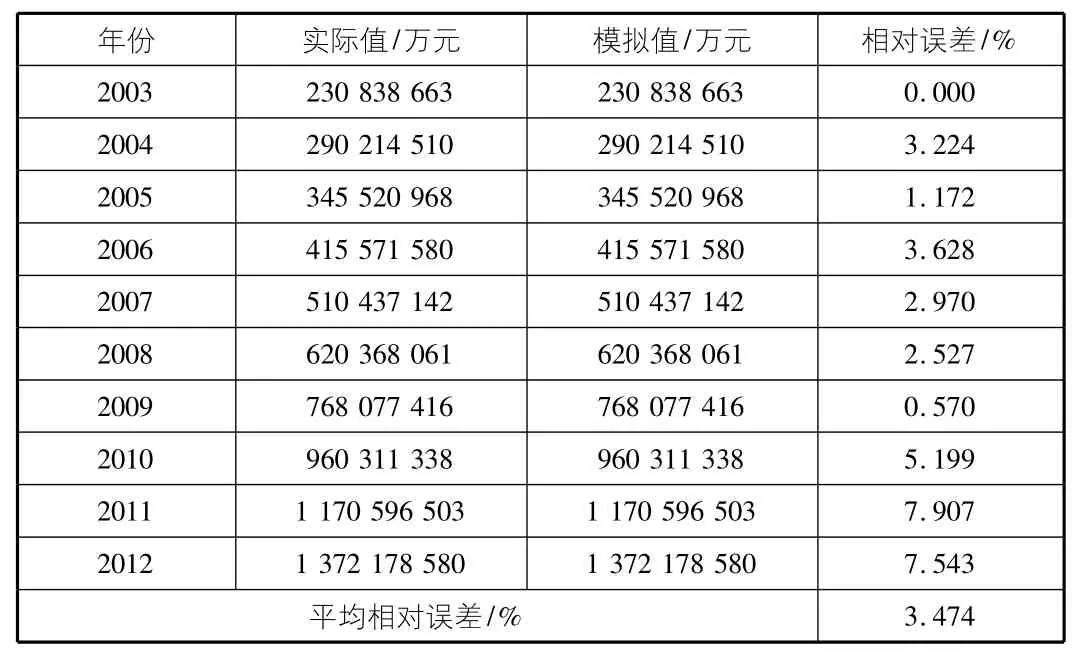
表1 建筑业总产值实际值与预测值对比

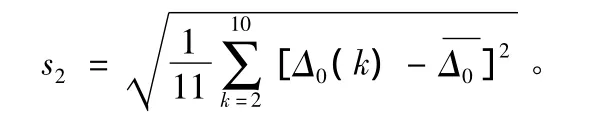
表2为2013年～2015年的建筑业总产值的预测值。按照现在的社会经济条件发展，到2015年全国的建筑业总产值将超过20万亿元。

以本文模型的预测结果作为决策的数据基础，可以了解建筑业的生产规模、发展速度、经营成果，制定相应的发展方案，使建筑业发展成为拉动国民经济快速增长的重要力量。

表2 2013年～2015年的建筑业总产值预测值 万元

4 结语

本文以GM(1，1)为基础，运用正弦函数变换有效提高原始数据序列的光滑度。同时提出了具有计算量小、计算简单、数字稳定性好的基于Lagrange插值的背景值的计算方法。分别从原始数据和背景值两方面进行改进，扩大了GM(1，1)的适应性。将优化后的模型使用在建筑业总产值预测中，取得了很好的预测效果。建筑业总产值预测给国家制订经济建设计划提供依据，便于合理制定建筑业发展目标，拉动国民经济快速增长，具有一定的实用性。

［1］温春红.浅谈中国建筑业经济增长影响因素［J］.科学与财富，2014(1):185.

［2］陈涛捷.灰色预测模型的一种拓广［J］.系统工程，1990，8(7):50-52.

［3］聂 艳，周 勇.基于拓广的GM(1，1)的土地变化情景研究［J］.数学的实践与认识，2007，37(3):10-11.

［4］戴文战，李俊峰.基于函数x－a的GM(1，1)模型及在我国农村人均住房面积建模中的应用［J］.系统工程理论与实践，2004，11(11):63-67.

［5］唐万梅，向长合.基于二次插值的GM(1，1)模型预测方法的改进［J］.中国管理科学，2006，14(6):109-112.

［6］刘 琦，袁鹏翔，高 冲.基于二次插值组合灰色预测模型的房价预测［J］.现代商业，2011(29):186-187.

［7］曹 昶，樊重俊.基于正弦函数变换的灰色预测模型研究及其应用［J］.数学杂志，2013，33(4):697-701.