沥青混合料疲劳损伤参数的反演与验证★

王波 韩丁

(1.安徽省高速公路控股集团有限公司，安徽合肥 230088;2.合肥工业大学，安徽合肥 230009)

0 引言

沥青混合料的疲劳性能多采用小梁疲劳试验进行研究，损伤力学是进行量化研究的有效理论手段。Sudip Bthattacharjee根据现场检测数据，采用损伤力学理论得出了沥青混凝土损伤演化规律［1］;Qiangluan Li对间接加载作用下沥青混凝土的疲劳寿命进行了研究［2］;Liantong Mo基于应力动态控制试验提出沥青粘结碎石的损伤累积模型［3］。道路工程领域损伤变量的定义应当采用以弹性常数、超声波速等为代表的宏观损伤变量。周志刚应用非线性有限元法，通过反分析得到沥青混凝土疲劳损伤演化规律［4］。钱国平通过沥青混合料的拉压疲劳试验，获得了考虑应力水平的拉压疲劳损伤演化方程［5］。使用损伤力学作为裂缝萌生的量化判定依据，并将断裂韧度作为沥青混凝土材料的开裂判断阀值，即可对沥青混合料小梁试件的疲劳过程进行分析。

1 试验概况

为了得到沥青混合料的断裂韧度，研究了预切缝小梁的三点弯曲断裂试验;为了得到沥青混合料的疲劳性能，研究了小梁的三点弯曲疲劳试验。

1.1 预切缝小梁断裂韧度的计算验证

根据文献资料［6］，沥青混合料的三点小梁弯曲断裂试验见图1。

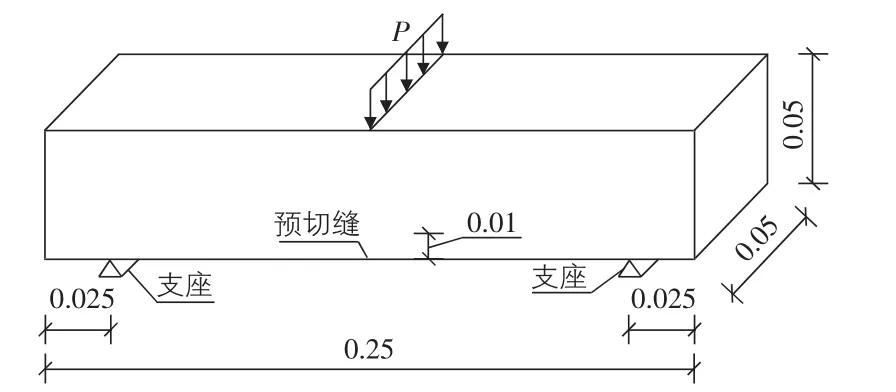
图1 沥青混合料的三点小梁弯曲断裂试验（单位：m）

根据静载试验结果，当跨中荷载为1.441 kN时，小梁的裂缝开始扩展，此时荷载作用位置的挠度为1.087 mm。泊松比选用0.3，根据15℃弯拉强度试验得到沥青混合料弯拉模量为935 MPa［7］。分别使用三维网格和二维网格对预切缝小梁试件进行划分，有限元模型见图2，预切缝尖端使用奇异单元。通过计算得到，在沥青混合料小梁的裂缝开始扩展时，三维单元预切缝尖端的极限拉应力为4.57 MPa，二维平面应变单元预切缝尖端的极限拉应力为4.54 MPa，预切缝尖端的拉应力分布见图3。

奇异点的应力强度因子值是通过不同围道的J积分计算得到的。通过比较距奇异点的距离分别为1.25 mm和5 mm积分围道的计算结果，可以确定三维模型和平面模型的网格划分已足够细化，计算结果已经稳定。图4通过对预切缝小梁应力强度因子进行有限元计算，比较了二维和三维模型的差异性。由试验得到沥青混合料加载开裂时的 Kc=0.28 MPa·m1/2［8］，采用平面应变单元计算的结果为Kc=0.256 MPa·m1/2。

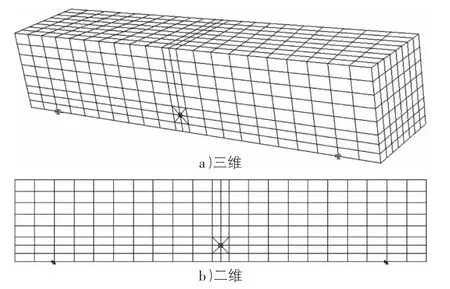
图2 预切缝试件的网格划分

图3 小梁预切缝起裂时的拉应力分布

图4 预切缝小梁应力强度因子有限元计算的有效性分析

三维模型的计算结果与平面应力模型和平面应变模型计算结果的最大差异处是小梁的纵向两侧，造成这种差异的原因是三维模型中纵向两侧单元的一侧是自由的，另一侧是受约束的(与另一排单元相连)，这种工况与平面应变和平面应力假定都存在较大差异，因此计算结果也就会有较大差异。在三维模型中间位置的一排单元，其工况与平面应变和平面应力假定较为接近，计算结果的吻合性也很好。因此，用有限元进行小梁预切缝尖端应力强度因子的计算是可行的。

1.2 沥青混合料小梁疲劳试验有限元建模

根据文献资料［8］，沥青混合料小梁三点弯曲疲劳试验的工况见图5。因为要模拟梁底在反复荷载下开裂的情况，对即将拉裂点的有限单元选定需要给予关注。现对小梁试件采用两种方案进行比较，一种是对梁底的最大受拉位置选用正方体单元，其特征长度a(mm)逐渐细化;一种是把梁底的最大受拉位置作为奇异点，其周围环绕布设奇异单元，如图6所示。

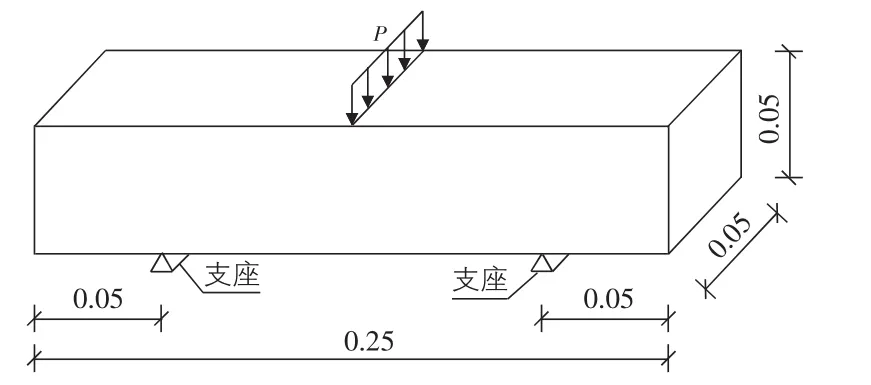
图5 沥青混凝土小梁三点弯曲疲劳试验（单位：m）

图6 小梁采用不同单元的三维建模

沥青混合料小梁的弯拉模量为935 MPa，泊松比为0.3，假设施加的跨中荷载为1 kN，梁底最大拉应力的结果见图7。

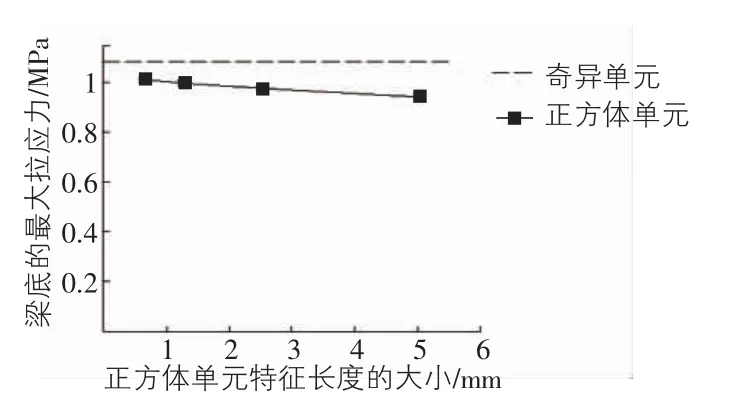
图7 采用不同单元的梁底最大拉应力

从图7可以看出，随着梁底正方体单元特征长度的减小，梁底的最大拉应力逐渐增大，逐渐接近于采用奇异单元的计算结果。由于起裂位置局限在趋向于某一点的很微小区域，正方体单元的无限细化并不可能。此外，当达到拉应力极限时，正方体单元出现失效，因此可以选用奇异单元来进行分析。

仍采用上面的相同工况对三维单元网格划分和平面应变单元网格划分的计算结果进行比较，计算得到的最大拉应力分别为1.08 MPa和1.06 MPa。由于在实际的路面结构分析中多采用平面应变单元，为了保持参数的适用性，使用平面应变单元。

2 断裂韧度为阀值的小梁疲劳分析

沥青混合料在损伤演化过程中，净应力随有效承载面积的减少而逐渐增大:

微裂缝的萌生和扩展会使循环加载下沥青混合料开裂区域的强度因子逐渐增大。

2.1 推导损伤演化方程

常采用双对数疲劳方程处理沥青混合料小梁弯拉疲劳试验数据:

学院成立“三师”型师资队伍建设领导小组，组长、副组长负责“三师”型师资队伍建设工作的组织、实施、协调。其他成员负责相关文件、方案、制度的起草、完善以及材料的收集、汇总和考核。每位专职教师负责在所任课班级搞好教学、时政宣讲、思政引导工作。学校层面的工作由领导小组安排落实。

其中，σf为重复应力;Nf为疲劳寿命;σs为弯拉强度;a，b均为系数。

式(2)可转化为:

其中，c=10a/(σs)b。

从式(3)可以看出，以应力为变量的幂函数可用来描述重复弯曲荷载下的小梁疲劳寿命，本文基于损伤变量使用相同的函数形式。沥青混凝土在道路工程中一般不会出现压缩破坏，所以只考虑拉伸损伤，因此提出的损伤演化方程为:

其中，a，b 均为系数。

道路结构能承受相当次数的车辆作用荷载，即一次荷载作用对路面结构造成的损伤很微小，因此可假定一次荷载作用下拉应力和损伤变量是线性关系，即系数b取为1.0。采用Miner线性疲劳累积方程，损伤演化方程的形式为:

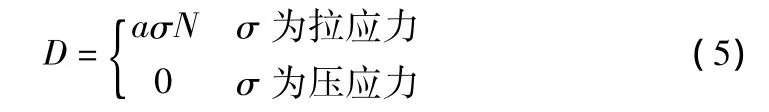
其中，a为系数;σ为应力;N为重复荷载作用的次数。

现在对系数a进行计算。进行疲劳试验的沥青混合料小梁，弯拉模量为935 MPa，泊松比为0.3。选用平面应变单元网格划分进行计算，当跨中作用4.45 kN荷载时，小梁开始出现裂缝。

表1 式(5)系数a的反算结果

在各级加载比的荷载重复作用下，起裂位置应力强度因子随不同加载比的重复荷载作用而发生的演化过程见图8。

分析图8的数据可以看出，随着加载次数的增加，应力强度因子呈现出加速的增长率。在较低加载比的荷载重复作用下，在先前相当一段时间内，梁底奇异点应力强度因子的演化相当缓慢，但达到一定次数后，该应力强度因子值迅速增长，说明确实存在一个疲劳极限。如果结构和材料设计得当，就可以保持沥青混合料的长期使用性能。

图8 不同加载比下起裂位置应力强度因子的演化

在不同加载比下，当荷载作用次数达到疲劳寿命时，小梁起裂位置的损伤分布和拉应力分布如图9和图10所示(程序自动插值会导致损伤变量出现负值和大于1的值)。

图9 不同加载比下小梁出现开裂时的损伤分布

可以看出，损伤区的分布区域随加载比的增加而逐渐集中，产生开裂时该区域内的损伤也不均匀。较低水平的加载比不仅有更高的疲劳寿命，而且在荷载的重复作用下还能充分使用材料整体性能。随着施加重复荷载的增大，起裂位置的应力强度因子迅速增加，材料整体未充分损伤就会达到断裂韧度，产生开裂。

路面结构使用过程中并不能对结构层底的拉应力值进行控制，因此需要根据表1数据对初次加载时的拉应力水平和系数a进行拟合，得到式(5)系数a的表达式:

其中，σ0为层底的拉应力，MPa。

将式(6)代入式(5)得到以应力为变量的沥青混合料损伤演化方程:

其中，N为荷载重复作用的次数。

2.2 损伤演化方程的验证

为了验证沥青混合料损伤演化方程的有效性，对方程进行了加载比0.4的内插预测，系数a由式(6)得到，并与试验数据［8］进行对比。

图10 不同加载比下小梁出现开裂时的拉应力分布

使用表1数据对S—N曲线法的疲劳方程进行拟合:

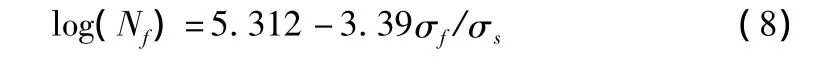
表2给出了S—N曲线法预测结果和疲劳寿命数值计算结果与试验数据的对比。可以看出，式(7)的沥青混合料损伤演化方程具有较好的疲劳寿命预测能力。使用损伤力学并以断裂韧度为阀值来描述小梁疲劳试验，可以量化实际道路结构的寿命预估问题。

表2 损伤演化方程验证的计算参数与结果

3 结语

1)结合沥青混合料小梁三点弯曲断裂试验的数据，可以通过设置奇异单元来计算沥青混合料的断裂韧度，且具有很好的精度。2)沥青混凝土小梁三点弯曲疲劳试验数据可用来反演损伤演化方程的参数，本构模型中包含损伤演化方程的有限元仿真具有良好的寿命预估精度。3)仿真结果可见沥青混合料在疲劳工况下存在一个疲劳极限，如果结构和材料设计得当，可以保持沥青混合料的长期使用性能。4)较低水平的加载不仅有更高的疲劳寿命，而且在荷载的重复作用下还能充分使用材料整体性能。随着施加重复荷载的增大，材料整体未充分损伤时起裂位置就会达到断裂韧度。

［1］Bhattacharjee S，Mallick R B.Determining Damage Development in Hot-Mix Asphalt with Use of Continuum Damage Mechanics and Small-Scale Accelerated Pavement Test［J］.Transportation Research Record:Journal of Transportation Research Board，2012(10):125-134.

［2］Li Qiangluan，Xiao Getian.Fatigue Life Analysis of Asphalt Mixture Coupling with Loading Intermittent Time［J］.Applied Mechanics and Materials，2012(8):3852-3858.

［3］Mo Liantong，Wu Shaopeng，Huurman M，et al.Damage accumulation model for monotonic and dynamic shear fracture of asphalt-stone adhesion［J］.Theoretical and Applied Fracture Mehcanics，2006，46(2):140-147.

［4］周志刚，张清平，袁秀湘.沥青混凝土弯曲疲劳试验疲劳损伤分析［J］.中南大学学报(自然科学版)，2011，42(6):1743-1751.

［5］钱国平，刘宏富，郑健龙，等.沥青混合料拉压疲劳损伤试验［J］.公路交通科技，2012，29(3):1-6.

［6］罗辉，朱宏平，陈传尧.预切口沥青混合料小梁疲劳试验与数值研究［J］.土木工程学报，2009，42(6):126-132.

［7］葛折圣，黄晓明.沥青混合料应变疲劳性能的试验研究［J］.交通运输工程学报，2002，2(1):34-37.

［8］武建民，李晓军.沥青混合料小梁疲劳试验的有限元模拟［J］.长安大学学报(自然科学版)，2004，24(1):5-8.