吊车支撑力学计算模型建立及编辑程序处理研究

李 强

(大秦铁路股份有限公司原平工务段，山西原平 034100)

0 引言

在国内外吊装施工过程中，经常会发生因吊车支撑失稳而引发的吊车折臂、倾覆等重大安全事故，因此吊车支撑的力学状态决定着吊车支撑的稳定性，是确保吊装施工安全非常关键的力学参数。然而在实际吊装施工作业过程中，现场工程技术管理人员存在着对吊车支撑力学计算理论不清楚、计算方法不科学的情况，本文就此问题进行了探讨与研究，并引入了利用计算机高级语言编辑程序处理的计算理念，可以在确保计算精度的条件下最大程度的减少计算难度及工作量。

1 吊车支撑力学计算模型及计算难度

1.1 吊车支撑力学计算模型

吊车吊装施工过程中，一般情况下是通过两轴(①号轴～②号轴、③号轴～④号轴)、四支撑(1号，2号，3号，4号)的共同作用来保证吊车的稳定性。吊装过程中的四支撑应力主要表现为竖向应力方向，吊车旋转吊臂过程中，四支撑(1号，2号，3号，4号)通过竖向应力(T1，T2，T3，T4)的即时变化来平衡吊重弯矩M。

1.2 吊车支撑力学计算难度

吊车支撑力学计算的目标是求解四支撑的竖向应力值:T1，T2，T3，T4，而使用力学静定平衡公式只能列出三个静定方程，即:竖向应力平衡方程、X方向弯矩平衡方程、Y方向弯矩平衡方程。因此吊车支撑力学计算是一个空间超静定问题，需使用工程力学中的“力法”“位移法”或其他工具(如:有限元分析法)等进行计算求解，这样便导致理论计算难度高、计算工作量大，无法满足在现场施工条件下使用及进行推广。

2 吊车支撑力学计算模型的简化分析

为了解决吊车支撑空间超静定力学计算难题，在保证基础理论分析正确及计算精度的前题下，对吊车支撑力学计算模型做了如下简化与假定:

1)吊重弯矩M分拆。

使用向量分拆的方法将吊重弯矩M分拆为X方向Mx，Y方向My。

2)假定吊装过程的两个阶段。

a.一阶段:吊车重心位于四支撑几何形心，吊车自重(含配重)及吊装物的总重由四支撑共同承担，即:原始单个支撑应力:

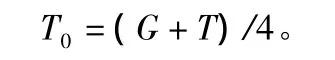
其中，G为吊车(含配重)的重量;T为吊装物的重量。

b.二阶段:由于Mx及My的作用引起吊车各支撑竖向应力ΔT1，ΔT2的变化(ΔT1，ΔT2可能为负值)，即:吊装过程中单个支撑应力为:TN=T0+ΔT1+ΔT2。

3)X方向假定。

将1号，3号支撑力T1，T3合并计为轴支撑力N1-3;将2号，4号支撑力T2，T4合并计为轴支撑力N2-4;由于Mx的作用轴支撑力N1-3减少ΔT1;由于Mx的作用轴支撑力N2-4增加ΔT1。

4)Y方向假定。

将4号，3号支撑力T4，T3合并计为轴支撑力N4-3;将2号，1号支撑力T2，T1合并计为轴支撑力N2-1;由于My的作用轴支撑力N4-3减少ΔT2;由于My的作用轴支撑力N2-1增加ΔT2。

5)使用力学静定平衡公式分别对X方向、Y方向进行分析求解，以得出ΔT1，ΔT2值，最终求解吊装过程中吊车各支撑应力TN。

3 吊车支撑力学计算公式的推导

根据吊车支撑力学计算的简化模型，以吊臂旋转作业范围在Ⅰ象限区工作进行了分析，进而求解四支撑的竖向应力:T1，T2，T3，T4值。

3.1 X方向分析求解ΔT1

轴支撑力N1-3向吊车重心取力矩:

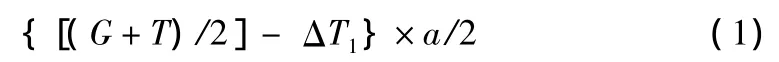
吊重弯矩M在X方向上的分量Mx:

轴支撑力N2-4向吊车重心取力矩:

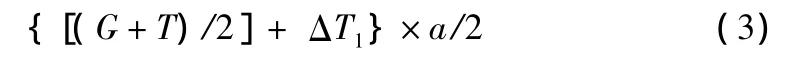
式(1)+式(2)=式(3)。

可得:ΔT1=T×L×sinθ/a。

3.2 Y方向分析求解ΔT2

轴支撑力N4-3向吊车重心取力矩:

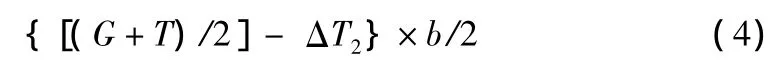
吊重弯矩M在Y方向上的分量My:

轴支撑力N2-1向吊车重心取力矩:

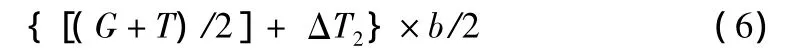
式(4)+式(5)=式(6)。

可得:ΔT2=T×L×cosθ/b。

3.3 求解吊车各支撑竖向应力 T1，T2，T3，T4 值

T1=［(G+T)/4］+［T×L×cosθ/(2×b)］－ ［T×L×sinθ/(2×a)］。

T2= ［(G+T)/4］+［T×L×cosθ/(2×b)］+ ［T×L×sinθ/(2×a)］。

T3= ［(G+T)/4］－［T×L×cosθ/(2×b)］－ ［T×L×sinθ/(2×a)］。

T4= ［(G+T)/4］－［T×L×cosθ/(2×b)］+［T×L×sinθ/(2×a)］。

其中，G为吊车(含配重)的重量;T为吊装物的重量;a为吊车支撑一侧宽度(平行于车纵向轴线);b为吊车支撑一侧宽度(垂直于车纵向轴线);L为吊车臂最不利水平作业半径;θ为吊车臂方向与Y轴夹角(平行于吊车车身方向)。

4 吊车支撑力学计算公式的分析

从推导出的吊车支撑力学计算公式中可以发现以下规律:

1)当吊车选型确定(即参数G，a，b确定)，吊装物重量确定(即参数T确定)，吊车最不利水平作业半径确定(即参数L确定)，则吊车各支撑竖向应力由转角θ确定，这便意味着吊车在吊重状态下进行旋臂作业，吊车各支撑竖向应力处于即时的动态变化过程中。

在工程实践时，需求解吊车应力最大支撑的最不利竖向应力值Tmax并结合地基承载力学参数，以便综合采取科学有效的吊车支撑加固措施。

2)吊车支撑力学计算公式受转角θ的影响，在Ⅱ象限区、Ⅲ象限区、Ⅳ象限区的表达形式与Ⅰ象限区略有不同，Ⅰ象限区四支撑中应力最大支撑为2号支撑。基于Ⅰ象限区计算公式经数学变换后可得出:Ⅱ象限区公式需将Ⅰ象限区计算公式转角θ变换为－θ，四支撑应力最大支撑为1号支撑;Ⅲ象限区公式需将Ⅰ象限区计算公式转角θ变换为π+θ，四支撑应力最大支撑为3号支撑;Ⅳ象限区公式需将Ⅰ象限区计算公式转角θ变换为π－θ，四支撑应力最大支撑为4号支撑。

5 利用计算机V-foxpro语言编程解决吊车支撑力学计算问题

虽然已经推导出了各象限区吊车支撑力学计算公式，但是在求解吊车应力最大支撑的最不利竖向应力值Tmax过程中却存在着重复计算，工作量大(频繁的代入θ值进行试算)、计算数据对比繁琐(需对比寻找数据拐点)等问题。而利用计算机高级语言编程计算则可以有效的解决此难题，使用计算机V-foxpro高级语言编程思想如下:

1)设计数据输入模块。

程序接收计算原始参数。如G为吊车(含配重)的重量;T为吊装物的重量;a，b为吊车支撑两侧宽度;L为吊车臂最不利水平作业半径。

2)设计各象限区吊车支撑力学计算模块。

a.根据吊臂作业范围选择吊车工作象限区域。

b.设定初始转角θ值(一般设置为0°);设计“累加计数器”及“累加计数器”精度(一般设置为1°);“累加计数器”计算机工作语言表达式为:θ=θ+1。

c.利用各象限吊车支撑力学计算公式，求解即时转角θ值状态下的吊车各支撑应力 TN值(T1，T2，T3，T4)。

d.利用V-foxpro高级语言“循环语句”，计算求解即时转角θ+1值状态下的吊车各支撑应力

3)设计计算数据逻辑对比模块。

a.确定工作象限区域应力最大支撑TN作为对比目标:Ⅰ象限区应力最大支撑为2号支撑、Ⅱ象限区应力最大支撑为1号支撑;Ⅲ象限区应力最大支撑为3号支撑;Ⅳ象限区应力最大支撑为4号支撑。

c.综合对比多个“计算拐点”，最大值则为最不利竖向应力值Tmax。

4)设计数据输入模块。

输出各“计算拐点”值及最不利竖向应力值Tmax;输出各“计算拐点”值及最不利竖向应力值Tmax对应的θ值。

5)根据最不利竖向应力值Tmax结合地基承载力学参数，对吊车各支撑采用针对性的预加固处理措施。如:增大支撑下受力面积;采用基础换填的方法增加地基承载能力;采用桩基础增加吊车支撑下承载能力等。

6 结语

采用理论计算的方法对吊车工作状态下的支撑竖向应力进行安全评估并针对性的采取工程预加固措施，可以使现场施工摆脱传统“施工经验指导”的盲目性束缚;而采用计算机编辑程序处理的思想，可以使工程技术人员摆脱纷繁复杂的理论推导与工程计算。近几年来，在我单位管辖范围内进行的多处大型桥梁架设施工过程中都采用了此方法，收到了良好的安全效益与经济效益。

［1］中华人民共和国铁道部.铁路工务安全规则［M］.北京:中国铁道出版社，2011.

［2］中华人民共和国铁道部.铁路技术管理规程［M］.北京:中国铁道出版社，2008.

［3］洪范文.结构力学［M］.北京:高等教育出版社，2008.

［4］谢膺白.visual foxpro 9.0程序设计教程［M］.西安:西安交通大学出版社，2007.