CFD空间精度分析方法及4种典型畸形网格中WCNS格式精度测试

涂国华，邓小刚，闵耀兵，毛枚良，刘化勇

（1.中国空气动力研究与发展中心 空气动力学国家重点实验室，四川 绵阳 621000；2.国防科学技术大学，湖南 长沙 410073；3.中国空气动力研究与发展中心 计算空气动力研究所，四川 绵阳 621000）

0 引 言

在计算流体力学（CFD）中，数值方法的精度阶数受内点格式、边界格式、网格质量和网格导数求解方法等影响，实际精度阶数通常小于离散格式的理论阶数。常用的精度分析方法有精确解法和虚构解法。但精确解通常是未知的，而虚构解法存在解的完备性问题且需要对控制方程进行修改。所以有必要发展一种能从数值解直接分析精度阶数的方法。

CFD常采用非线性格式，非线性格式由于具有限制器或模板自适应选择器等，其精度通常并不等于与之对应的线性格式（比如取优化权值的格式）。即使在光滑流场，非线性格式的精度通常也要比对应的线性格式的精度低。非线性加权紧致格式［1－3］（WCNS）是邓小刚等在20世纪90年代提出的高阶精度且能光滑捕捉激波的有限差分格式。首先，他们通过在中心型紧致格式中加入耗散项，于1996年构造了单参数线性耗散紧致格式（DCS）［4］，通过调整单一参数，精度可达到3至9阶。同时，他们又提出了自适应插值的概念，构造了一类高阶非线性紧致格式（CNS）［5］，这样可以解决 DCS很难用于含有激波流场的困难。然后通过引入加权插值思想，构造了一系列WCNS，包括隐式和显式两种类型。其中5阶显式 WCNS格式（WCNS－E－5）由于不需要求解3对角矩阵，被大量用来模拟各种流动问题。

早年的Fourier分析表明，在优化权值情况下，5阶WCNS比5阶WENO的分辨率稍高、数值耗散略小［2］。最近，文献［6］的分析表明在非线性权值情况下WCNS格式的优势更明显。Nonomura等［7］比较了WCNS和WENO的自由流守恒和涡量守恒特性，发现WCNS在这两个方面的都比WENO强，且在曲线坐标系下WCNS的优势更加明显。Visbal［8］和邓小刚等［9］发现面积守恒律（SCL，Surface Conservation Law）对有限差分格式非常重要。邓小刚等［9］还发展出了一套满足SCL的网格导数守恒算法（CMM，Conservative MetricMethod），WCNS可以满足SCL，但是 WENO 还存在困难。目前，Nonomura［10－11］和Zhang［12］等还发展出了精度更高的 WCNS。迄今为止，WCNS已经解决了大量复杂网格中的复杂流动问题并取得了较好效果［13－15］。

航空航天飞行器的外形通常都较为复杂，网格也必定非常复杂，相应的网格拓扑结构也是形式各异。我们从复杂网格中提炼出4种典型畸形网格：斜交、拉伸、拐折和扭曲。通过这4种网格的叠加可以构造出各种各样的复杂网格。为了直接从计算结果分析空间离散格式的精度，本文给出了两种方法，一种方法适合精确解已知的情况，另一种方法适合精确解未知的情况。由于数值解已经包含了复杂网格的非均匀、非正交等的影响，所以这两种方法把与空间离散有关的信息都自动包含在内，体现了空间离散（含网格导数离散和边界格式）的整体精度。本文最后在斜交、拉伸、拐折和扭曲网格上考察了 WCNS－E－5格式的数值精度，计算结果表明该格式能达到高阶精度。

1 WCNS－E－5格式

曲线坐标系下的守恒型Euler／N－S方程可以表示成：

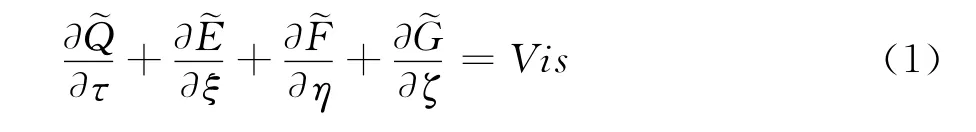
其中Vis表示粘性项。

对流项离散采用原始变量型的 WCNS－E－5格式，设网格间距为h，以ξ方向为例

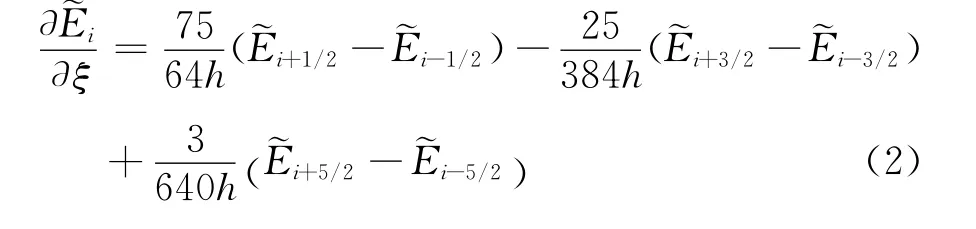
设U为流场变量，上式中：

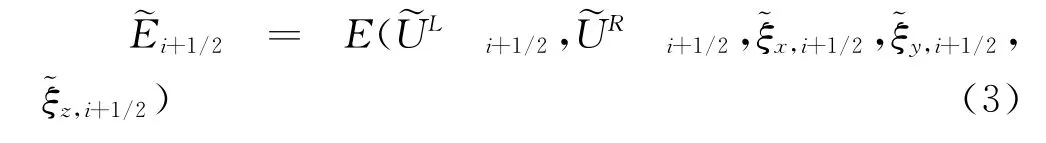
其中半节点上网格导数通过高阶精度的中心插值方法求得（本文采用4阶），半节点上的变量通过5阶非线性加权插值求得，具体情况请参考文献［2］。本文采用了3阶精度的边界差分格式，具体详情请参考文献［2］和［14］。

对于粘性流动，粘性项采用文献［16］的4阶精度交错差分方法。

2 格式精度的数值分析方法

2.1 格式精度简介

采用数值方法对微分方程进行离散逼近时，数值解与真实解之间存在一定误差，该误差与网格间距相关。假设采用m阶精度格式离散一阶导数∂f／∂x，它与精确解存在如下关系：

在忽略高阶小量的情况下，可以得到离散误差：

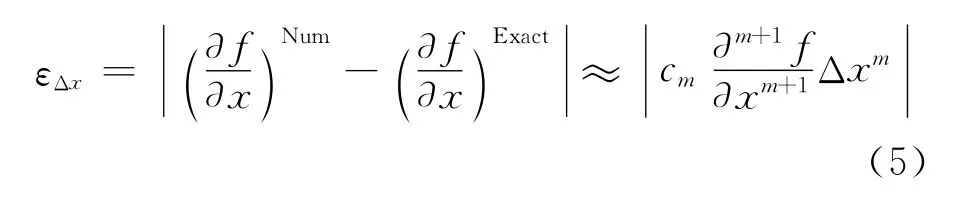
可见格式精度体现的是计算误差随着网格间距的收敛速度。随着网格间距Δx趋于零，计算误差εΔx以m阶的指数速度向零收敛。误差的绝对值大小还与f的m＋1阶导数和系数cm有关，但这两个参数都不随网格间距变化。两套网格的误差比为：

上式取对数可以得到精度m：

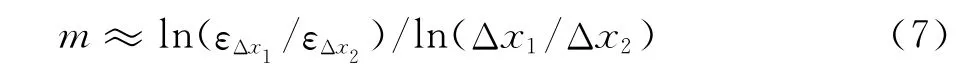
但是，通过上述思想得到的精度计算方法具有3个缺点：（i）由于计算区域的某些位置会出现f的m＋1阶导数等于0的情况，式（7）在这些地方会出现奇异。（ii）边界格式与内点格式不同且对整个流场都有影响，为了达到流场的整体计算精度，双曲方程的边界格式精度最多只能比内点格式精度降1阶［17］，上述这种方法无法从全局考察边界格式的影响。（iii）实际计算时，难免会出现局部区域的计算误差在稀网格上小，在密网格上大，所以计算精度出现一定的随机分布，如文献［18］中的计算结果。上述3点是文献［18］和［19］中精度分析方法的主要缺陷，需要发展新的精度分析方法。

2.2 已知精确解的情况

本文只考虑空间离散格式的精度，方程（1）在空间离散后的修正方程可以表示成：

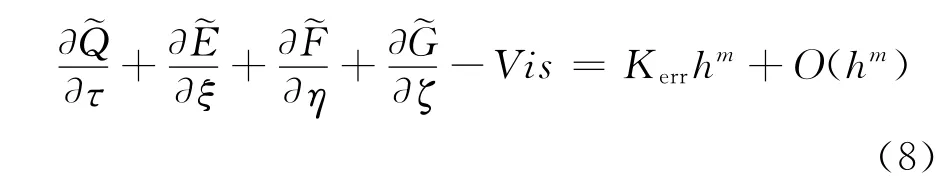
此处h为网格的特征尺寸，Kerrhm表示首项截断误差，上标“m”表示空间离散的精度，Kerr为首项截断误差的系数。

式（8）是建立在曲线坐标系下的，非均匀网格需要通过坐标变换转换成曲线坐标系下的均匀网格。但是，由于网格本身可能不连续，导致变换后的网格导数不连续。高阶精度格式要求网格也是高阶光滑的，光滑阶数应不低于格式精度［20］。但是这个条件太过苛刻，所以对于高阶精度格式，实际计算精度并不等于格式精度，而是网格与格式紧耦合后的精度，即不同网格可能导致精度不同。当网格质量不满足要求时，式（8）右端还应该包含网格离散带来的误差，比如面积不守恒（SCL不满足）的误差也应该包含在内。文献［9］给出了面积不守恒的误差表达式。

从式（8）可以看出，某套网格下数值解的误差Err即为（只考虑首项截断误差）：

假设有两套特征尺寸为h1和h2的网格，这两套网格的误差相除并取对数可得空间离散后的实际精度为：

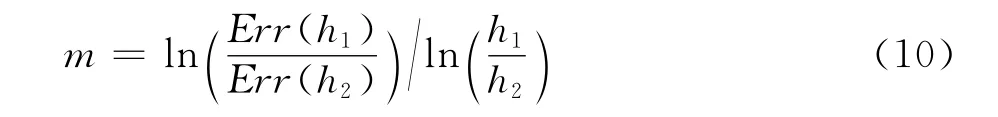
对于均匀网格，特征尺寸h可以取网格中任意两个点之间的距离，比如Δx。对于与非均匀网格，若两套网格的拓扑结构完全一致，可以取

此处N为网格单元总数。D＝1，2，3分别对应1维、2维和3维情况。

若已知两套网格上的数值解和精确解，便可通过式（10）求得计算格式的精度。为了避免平凡解（或平凡点）的影响，数值分析采用泛函的形式，其中Err（h）＝Ln（UNum－UExa）通过对误差取Ln范数求得，常用L1、L2和L∞范数。

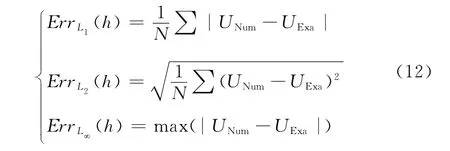
其中UNum表示数值解，UExa表示精确解。

采用式（10）求解空间计算格式的精度时，并不要求h1和h2存在倍数关系，但是，为了减小误差，两套网格的拓扑结构应该相同。

2.3 未知精确解的情况

若精确解未知，式（10）不再适用，也不能通过两套网的计算解来求得空间格式的精度，此时需要3套网格。假设稀、中、密三套网格的特征尺寸分别为h1、h2和h3。数值解可以表示成：

其中εh为数值解误差，且只取首项截断误差εh＝Kerrhm，于是

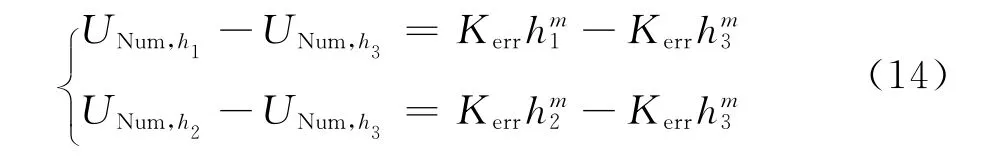
对上式取范数可得

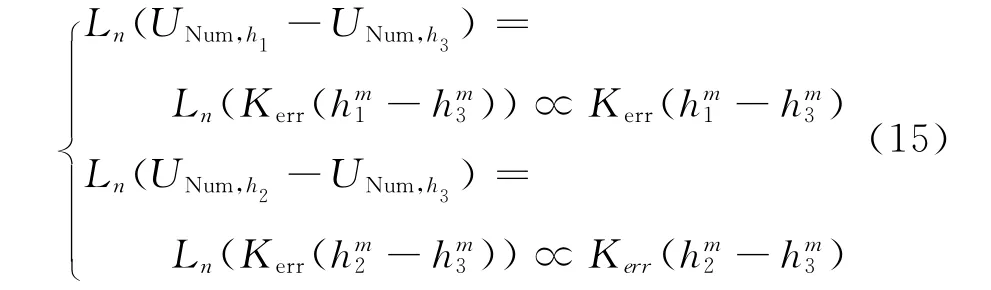
两式相除可得

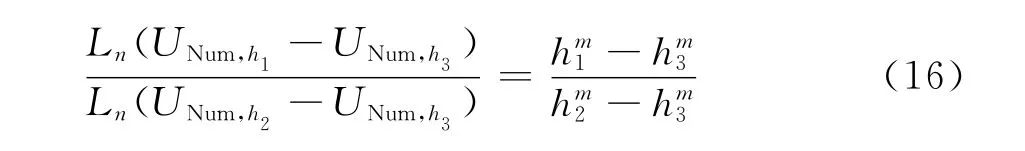
上式即为未知精确解时格式精度的数值求解方法，它在0阶精度附近的误差较大。为了减小系统误差，在使用上式时要求这三套网格的拓扑结构完全一致，h1、h2和h3成倍数关系，且有重叠点。另外还需要注意的是，在求Ln（UNum，h2－UNum，h3）时，并不是对所有网格节点上的值都采样，而是只对与稀网格相重合的节点采样。

不管是采用式（10）还是式（16），都要求网格密度足够分辨所考察的物理信息，比如对于有限差分格式，每个波长至少要布置4个网格点。

网格变换也会导入误差，如果这类误差远小于计算格式的离散误差，或者可以表示成网格尺寸的指数形式（即hn），那么式（10）和式（16）仍然适用；否则，不能保证式（10）和式（16）的正确性。

式（16）在如下两种特殊情况下还可以进一步简化：

（1）高精度格式情况

假设稀、中、密三套网格依次1倍加密，式（16）可化为

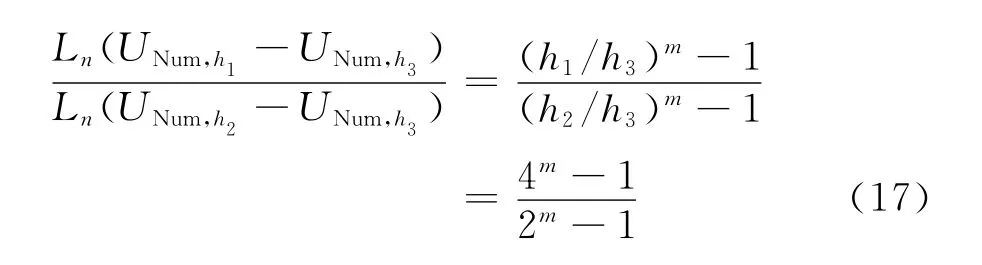
对于高精度格式，则有2m≫1，上式可以近似为

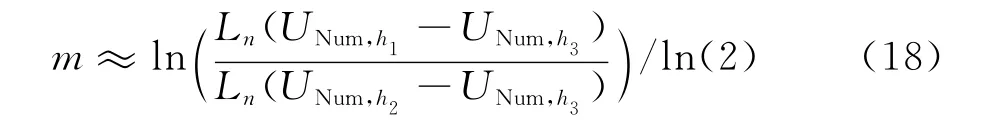
（2）密网格远比中等密度网格密的情况

若密网格非常密，即h3≪h2，则可以把密网格上的值当成精确值，式（16）可以简化为

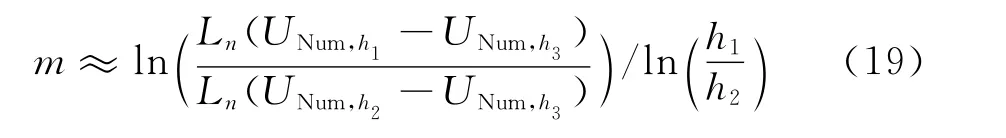
即与式（10）非常类似。

3 WCNS－E－5格式的精度测试

3.1 斜交网格

以二维线性波动方程为例

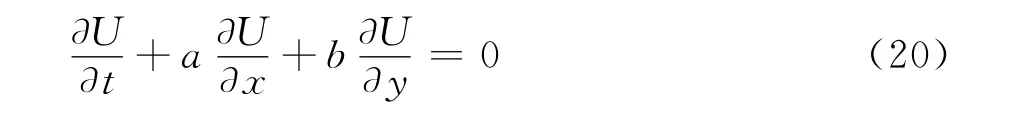
其中a、b为常数，不失一般性，假定a、b＞0。通过坐标变换（x，y，t）→（ξ，η，τ）得到曲线坐标系下的二维线性波动方程

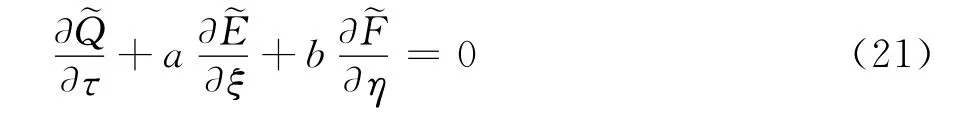
考虑图1所示的斜交网格，为了推导方便，假设两个方向的网格纵横比n＝1，易知：

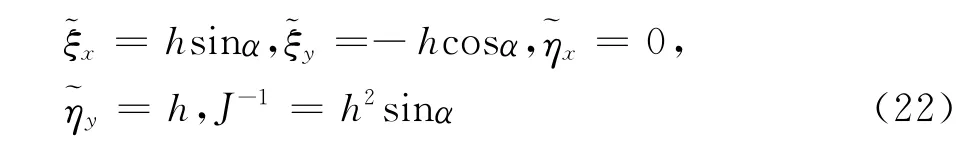
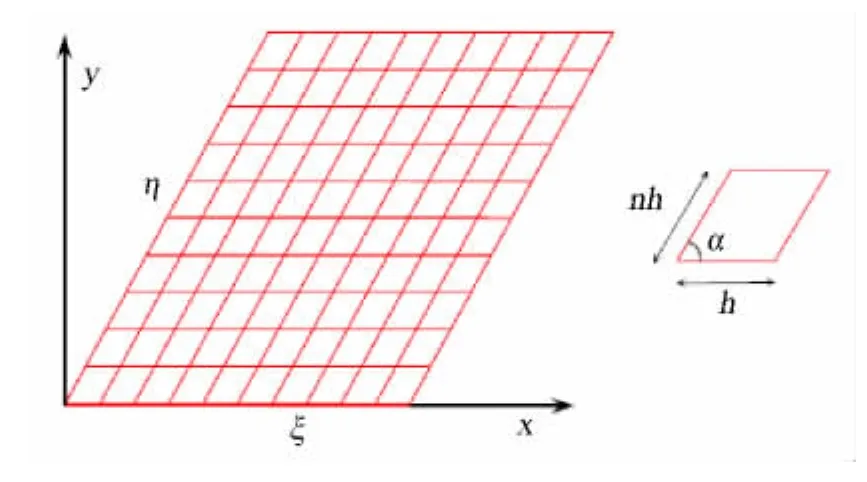
图1 斜交网格Fig.1 Oblique crossed mesh

WCNS－E－5的最优插值公式①本文仅在此处采用了最优插值，在其他地方都采用非线性插值。

通过推导可以得到控制方程（21）在采用最优插值的WCNS－E－5格式离散后的修正方程为：

此处其中ax＝nxπ／H，ay＝nyπ／H。nx、ny分别为x、y方向上的波数，H表示计算区域长度，计算采用了周期边界条件。我们在10°～170°斜交网格中对 WCNS－E－5格式的精度进行了考察，图2给出了α＝60°时的初值，表1给出了60°斜交角度下的误差和采用式（10）与式（16）得到的精度，其他斜交网格下的计算精度与60°斜交网格相同，此处不再给出。由表1可见，数值

可见为5阶精度。通过类似的证明还可以得到网格纵横比n≠1时的精度也为5阶。

设计如下初值计算精度为5阶，与理论分析结果完全吻合，既验证了WCNS－E－5格式在求解线性波动方程时能达到5阶精度，又验证了式（10）和式（16）的正确性。

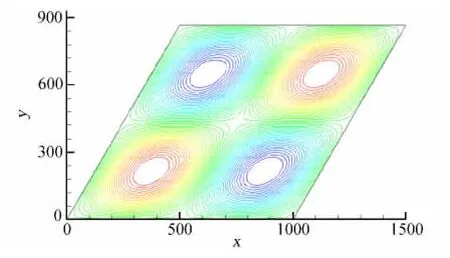
图2 二维波动方程的一个初值Fig.2 Initial value of two－dimensional wave equation

图3给出了等熵涡在45°斜交网格中的传播情况，此时的控制方程为Euler方程。表2给出了误差和精度，此表同样表明采用式（10）和式（16）求得的精度是一致的，同时还表明WCNS－E－5格式在求解Euler方程时具有接近5阶的精度。

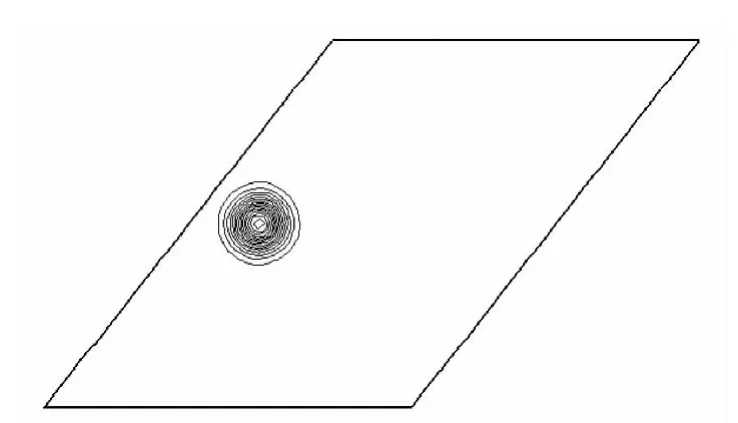
图3 等熵涡在45°斜交网格中的压力等值线（周期边界）Fig.3 Isentropic vortex in 45°inclined mesh

3.2 拉伸网格

模拟边界层流动时，为了节省网格量，通常在物面附近对网格进行加密，拉伸网格就是一种常用的方法。

首先考察一个等比拉伸网格的情况。给定一个初始拉伸比为λ1的粗网格，称为第一套网格；第二套网格是在第一套网格的任意两点之间插入一个新点得到的加密一倍的网格；第三套网格又以第二套网格为基础进行加密，依此类推。为了保证网格的相似性，第k套网格与第k－1套网格的拉伸比是不一样的。容易得到两套网格的拉伸比满足：λk＝。这样生成的网格可以保证每相邻两套之间都有重叠点，有利于采用数值方法进行精度分析。

数值实验采用一维Burgers方程：本文取Re＝20。边界条件：在x＝0的地方u＝1；在x＝1的地方u＝0。图4给出了在此边界条件下Burgers方程的解，可见与边界层速度剖面相似。表3给出了初始网格拉伸比为λ1＝2时的格式精度，可见精度为4阶左右，与粘性项差分格式的精度相当。

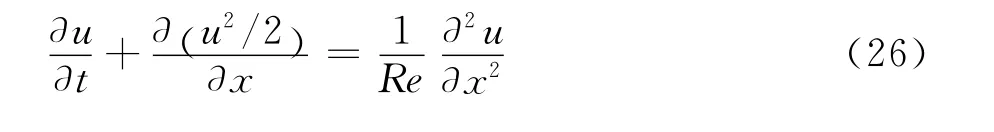
表1 60°斜交网格时WCNS－E－5格式得到二维波动方程的误差和数值精度Table 1 Errors and accuracy order of WCNS－E－5for two－dimensional wave equation on 60°oblique crossed meshes

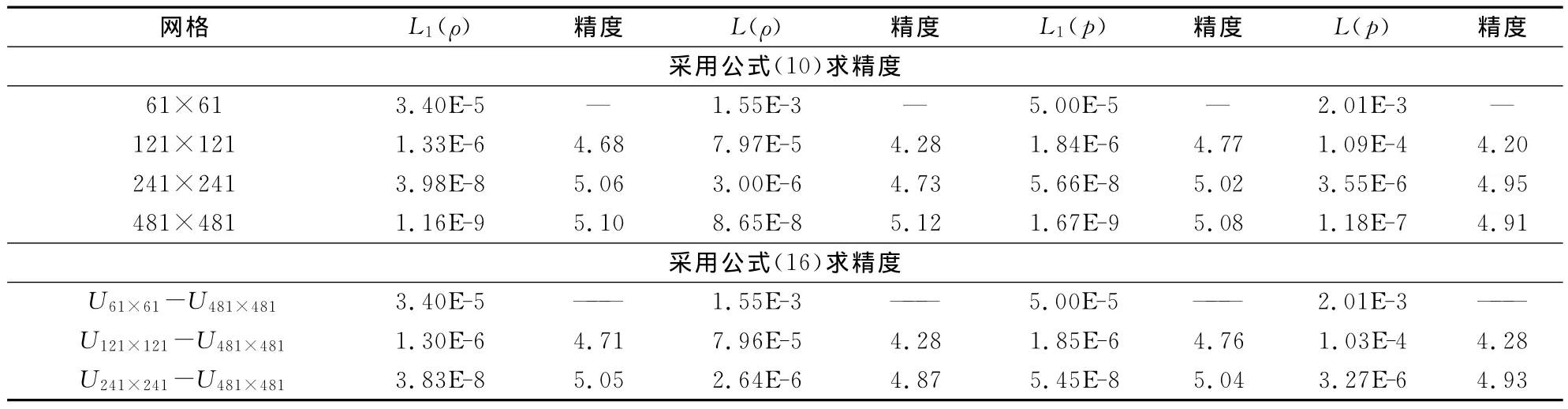
表2 WCNS－E－5格式在45°斜交网格中模拟等熵涡的误差和数值精度Table 2 Errors and accuracy order of WCNS－E－5for isentropic vortex problem on 45°oblique crossed meshes

再以超声速平板层流边界层为例，控制方程为N－S方程。网格和计算结果见图5。Ma＝4，Re＝1E＋4。入口边界和上边界给定3层来流值。物面为无滑移等温壁Tw＝300K，同时采用3阶精度的边界格式通过∂p／∂n＝0求得压力。出口采用3阶精度外推。

计算采用了3套网格，首先采用Gridgen制作了网格节点总数为121×121的网格，然后隔点取值生成了61×61和31×31的网格。另外，在每套网格的平板前缘添加了5层网格点以便捕捉前缘激波。

为了减小远场边界、出口边界和激波的影响，以图5（b）中深蓝色小方框区域为求解精度的参考区域。计算得到的精度如表4所示，为3阶左右。但是，除边界格式为3阶外，其他地方的精度都不低于4阶：内点无粘项的计算格式为5阶、粘性项和网格导数的计算格式都为4阶。计算结果的精度降价现象可能受激波影响，也可能受边界格式的影响，或是Gustaffson［17］关于边界格式可以比内点格式低1阶精度的结论仅对双曲方程成立，具体原因还需要深入分析。

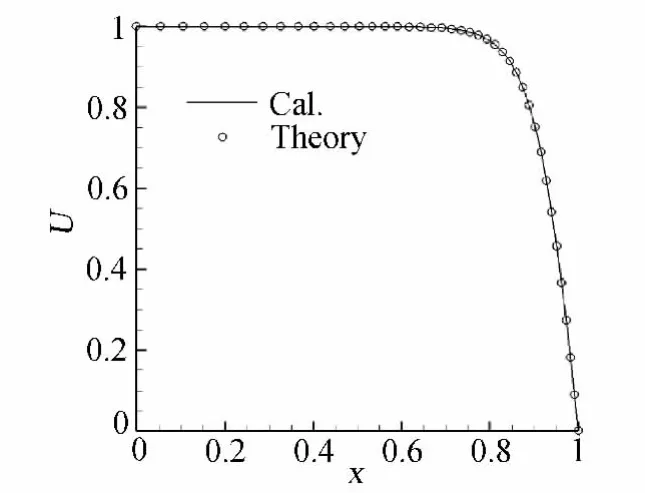
图4 Burgers方程的一个解Fig.4 A solution of Burgers equation

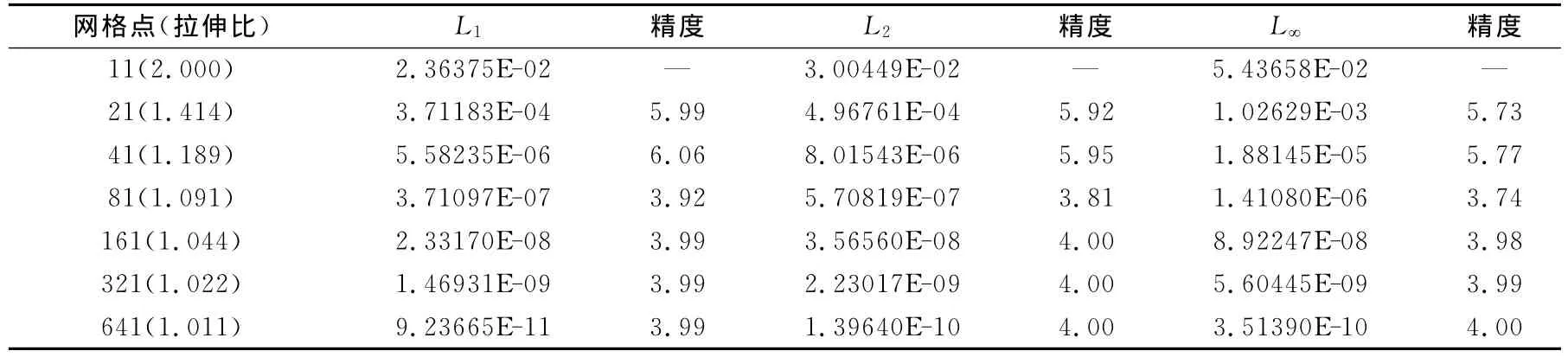
表3 拉伸网格中的WCNS－E－5的误差和数值精度Table 3 Errors and accuracy order of WCNS－E－5on stretched meshes

表4 WCNS－E－5计算超声速边界层的精度Table 4 Accuracy order of WCNS－E－5for supersonic boundary layer

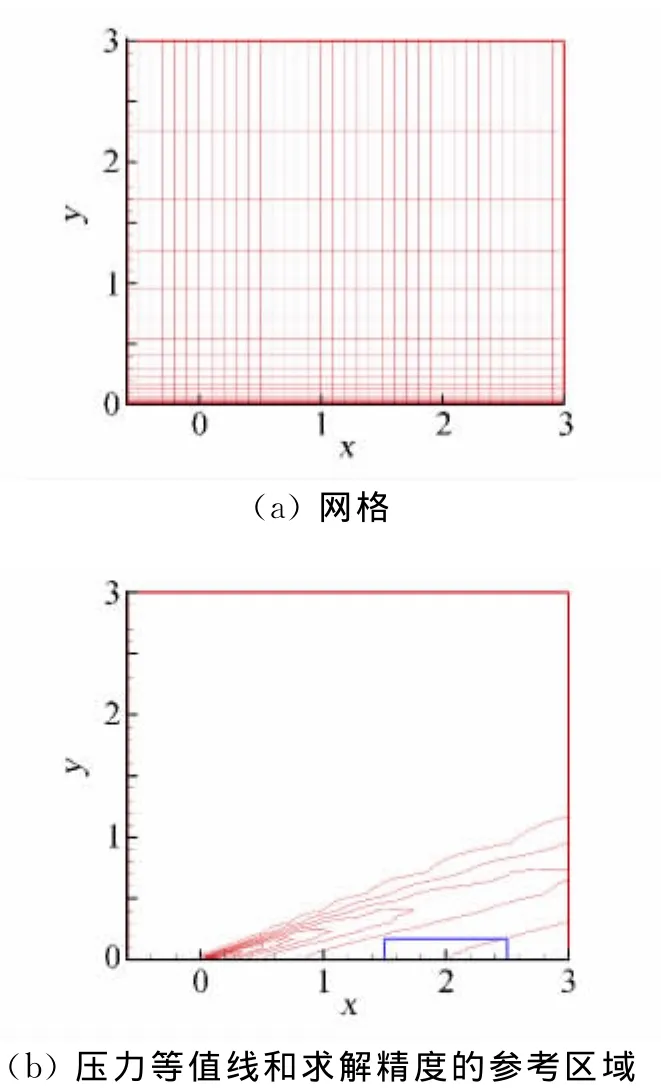
图5 超声速平板的网格和计算结果Fig.5 Mesh and numerical result of supersonic boundary layer

3.3 拐折网格

如图6所示，拐折网格可以分为两种，第一种是间断拐折，第二种是渐进拐折。这两种拐折情况都是由于飞行器几何外形拐折引起的。对于流线型外形，通常是渐进拐折，但是拐折曲率与飞行器特征尺寸相比可能很小。有时候为了处理方便，数值计算时常把小曲率半径拐折当成间断拐折处理。由于间断拐折的网格导数在拐折处不连续，为了保证高阶精度，常常需要在拐折处进行网格分块，块与块之间可以通过某种对接技术处理。邓小刚等人曾经发展了一种特征对接方法［14］，很适合用来处理这种情况。对于渐进拐折，由于网格导数本身是连续的，按单块网格处理即可。

以等熵涡的传播来考察精度，图7给出了 WCNS－E－5在这两种拐折网格中的计算结果。表5给出了误差和精度，可以看出，整体计算精度为4阶，比边界格式精度高1阶，即数值计算双曲方程时，整体精度可以比边界格式高一阶。

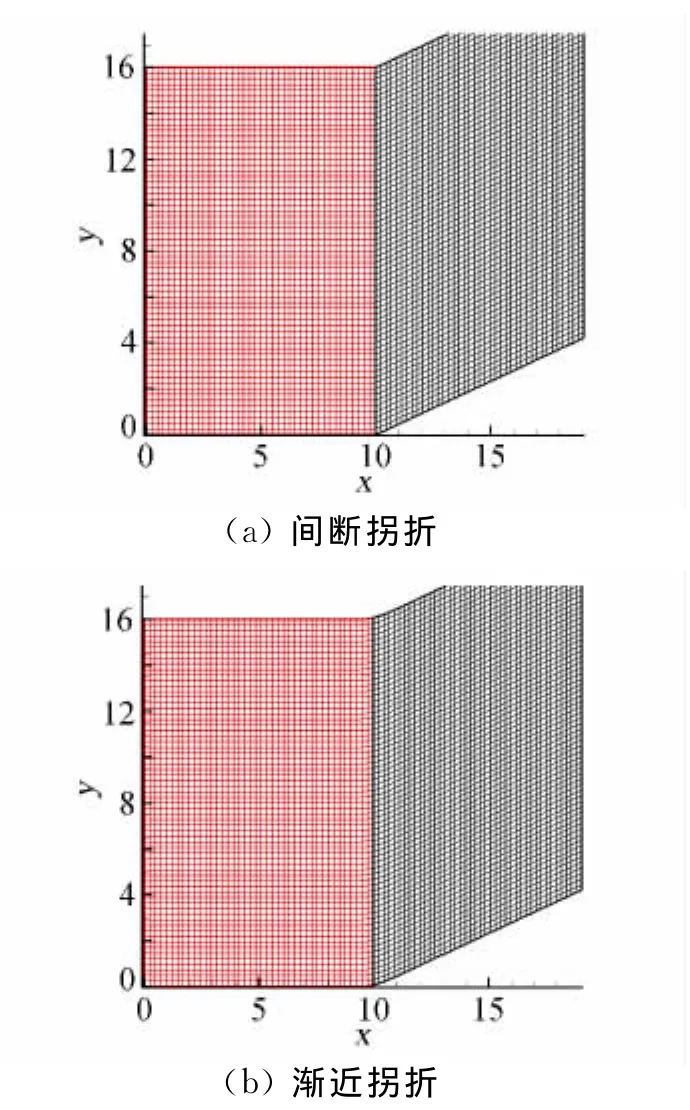
图6 两种25°拐折网格Fig.6 Two cornered meshes with the corner angle of 25°

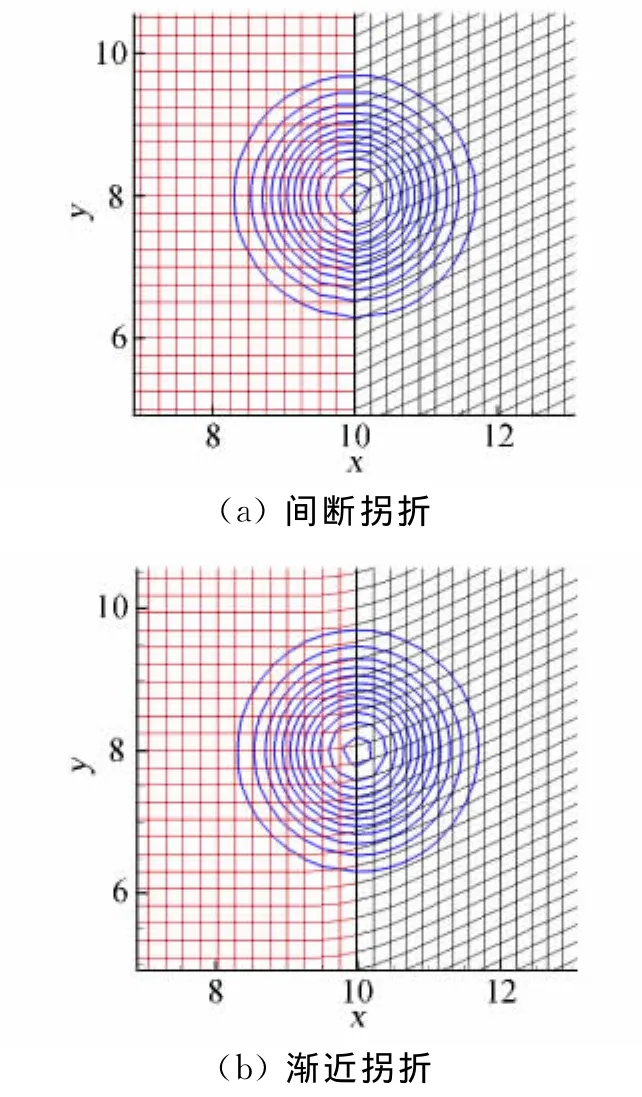
图7 等熵涡在拐折网格中的压力等值线（边界格式3阶精度）Fig.7 Pressure contours of isentropic vortex on two cornered meshes（Boundary scheme is third－order accurate）

3.4 扭曲网格

网格如图8（a）所示，生成公式与文献［8］相同。仍然通过等熵涡的传播来考察精度，图8还给出了压力等值线和误差收敛曲线。为了消除边界格式的影响，计算过程中采用了周期边界。表6给出了误差和精度，可见基本上接近5阶精度。

表5 拐折网格中WCNS－E－5的误差和数值精度（以密度为参考量）Table 5 Errors and accuracy order of WCNS－E－5for cornered meshes（based on density）

表6 扭曲网格中WCNS－E－5的误差和数值精度（以密度和速度v为参考量）Table 6 Errors and accuracy order of WCNS－E－5for skewed meshes（based on density and velocity v）

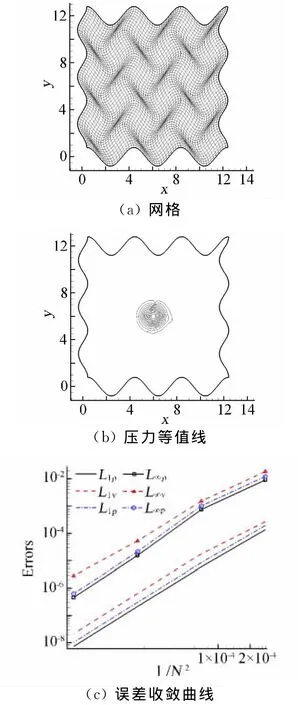
图8 61×61扭曲网格和WCNS－E－5计算得到的压力分布和收敛曲Fig.8 61×61skewed mesh，pressure contours and grid convergence lines of WCNS－E－5

4 结 论

CFD的实际计算精度阶数受计算格式、网格、边界处理等影响。CFD的算法通常为非线性格式，非线性格式由于具有限制器或模板自适应选择器等，与所对应的线性格式相比，通常耗散增加，分辨率降低，精度降低。当采用非线性格式在复杂网格上计算实际流动问题时，网格质量和边界处理还会对最终计算精度造成一定影响。但是，很难从理论上分析非线性格式在曲线坐标系下求解非线性偏微分方程的精度。本文首先给出了两种利用数值计算结果反推计算格式精度的方法，一种方法适合已知精确解的情况，另一种方法适合未知精确解的情况。

本文把复杂网格提炼成4种典型畸形网格：斜交、拉伸、拐折和扭曲。通过线性波传播问题、涡传播问题和边界层问题等对非线性 WCNS－E－5格式的精度进行了考察。结果表明，WCNS－E－5内点格式在这4种网格中都实现了接近5阶的精度。但是，边界格式对整体计算精度具有明显影响。若采用3阶精度的边界格式，能在求解Euler方程时达到4阶精度。

［1］DENG X G，MAO M L.Weighted compact high－order nonlinear schemes for the Euler equations［R］.AIAA Paper 97－1941.

［2］DENG X G，ZHANG H X.Developing high－order weighted compact nonlinear schemes［J］.JournalofComputational Physics，2000，165：24－44.

［3］DENG X G.High－order accurate dissipative weighted compact nonlinear schemes［J］.ScienceinChina（SeriesA），2002，45（3）：356－370.

［4］DENG X G，MAEKAWA H，SHEN C.A class of high order dissipative compact schemes［R］.AIAA Paper 96－1972.

［5］DENG X G，MAEKAWA H.Compact high－order accurate nonlinear schemes［J］.JournalofComputationalPhysics，1997，130：77－91.

［6］TU G H，DENG X G，MAO M L.Spectral property comparision offifth－order nonlinear WCNS and WENO difference schemes［J］.ACTAAerodynamicaSinica，2012，30（6）：709－712.（in Chinese）涂国华，邓小刚，毛枚良.5阶非线性WCNS和WENO差分格式频谱特性比较［J］.空气动力学学报，2012，30（6）：709－712.

［7］NONOMURA T，IIZUKA N，FUJII K.Freestream and vortex preservation properties of high－order WENO and WCNS on curvilinear grids［J］.ComputersandFluids，2010，39：197－214.

［8］VISBAL R M，GAITONDE D V.On the use of higher－order finite－difference schemes on curvilinear and deforming meshes［J］.JournalofComputationalPhysics，2002.181：155－185.

［9］DENG X G，MAO M L，TU G H，et al.Geometric conservation law and applications to high－order finite difference schemes with stationary grids［J］.JournalofComputationalPhysics，2011，230（4）：1100－1115.

［10］NONOMURA T，FUJII K.Effects of difference scheme type in high－order weighted compact nonlinear schemes［J］.Journalof ComputationalPhysics，2009，228：3533－3539.

［11］NONOMURA T，FUJII K.Robust explicit formulation of weighted compact nonlinear scheme［J］.ComputersandFluids，2012，http：／／dx.doi.org／10.1016／j.compfluid.2012.09.001.

［12］ZHANG S H，JIANG S F，SHU C－W.Development of nonlinear weighted compact schemes with increasingly higher order accuracy［J］.JournalofComputationalPhysics，2008，227：7294－7321.

［13］FUJII K，NONOMURA T，TSUTSUMI S.Toward accurate simulation and analysis of strong acoustic wave phenomena－a review from the experience of our study on rocket problems［J］.InternationalJournalforNumericalMethodsinFluids，2010，64：1412－1432.

［14］DENG X G，MAO M L，TU G H，et al.Extending weighted compact nonlinear schemes to complex grids with characteristic－based interface conditions［J］.AIAAJournal，2010，48（12）：2840－2851.

［15］DENG X G，MAO M L，TU G H，et al.High－order and high accurate CFD methods and their applications for complex grid problem［J］.CommunicationinComputationalPhysics，2012，11：1081－1102.

［16］TU G H，DENG X G，MAO M L.A staggered non－oscillatory finit difference method for high－order discretization of viscous terms.［J］.ACTAAerodynamicaSinica，2011，29（1）：10－15.（in Chinese）涂国华，邓小刚，毛枚良.消除粘性项高阶离散数值振荡的半结点－结点交错方法［J］.空气动力学学报，2011，29（1）：10－15.

［17］GUSTAFFSON B.The convergence rate for difference approximations to mixed initial boundary value problems［J］.MathematicsofComputation，1975，29（130）：396－406.

［18］ROY C J，MCWHERTER－PAYNE M A，OBERKAMPF W L.Verification and validation for laminar hypersonic flowfields［R］.AIAA paper 2000－2550.

［19］DE VAHL DAVIS G.Natural convection of air in a square cavity：a bench mark numerical solution［J］.InternationalJournal forNumericalMethodsinFluids，1983，3（3）：249－264.

［20］CHENG J，SHU C－W.High order schemes for CFD：a review［J］.ChineseJournalofComputationalPhysics，2009，26（5）：633－655.