一种基于三阶WENO重构的无网格算法研究

蒲赛虎，陈红全

（南京航空航天大学 航空宇航学院，江苏 南京 210016）

0 引 言

无网格算法是继网格算法之后出现的一种新型数值计算方法。在剖分计算区域时，由于只涉及布点填充，既可以利用传统网格算法采用的网格点，也可以在需要的前提下直接布点，在处理复杂外形方面，更具有灵活性［1－3］。

Batina［1］自20世纪90年代初就开始无网格算法的应用研究，提出用点云离散计算区域，代替通常的网格划分，并在当地点云上，利用最小二乘法逼近计算空间导数，由此发展出基于Jameson中心格式的无网格算法。但中心格式一般数值耗散较大，而且为了抑制高频振荡等还必须加入人工粘性项。为了克服上述不足，Morinishi通过在点云的卫星点连线中点处引入交界面，将一种逆风型的Roe格式引入到无网格算法中，减小了数值耗散，同时通过线性逼近重构交界面左右状态值，使得算法能达到二阶精度［2］。之后，许多学者针对具体的求解问题，分别将不同的逆风型格式引入到无网格算法中［4－6］，但整体上对于算法涉及的交界面左右状态值的确定，大多是基于线性逼近重构，因此其计算精度至多能达到二阶。用高阶的界面逼近重构替代传统的无网格线性逼近重构，应有助于提高无网格算法的求解精度。

本文考虑在无网格算法中，引入发展相对成熟的WENO（Weighted Essentially Non－Oscillatory）重构。该重构法最早是由Liu等人［7］在ENO重构［8］的基础上发展而来，它将ENO重构选择最光滑模板进行数值逼近的处理方法，改进为对所有模板的数值逼近进行加权求和，通过构造合适的权系数，在光滑区域可以达到比ENO重构更高的精度，且具有更好的收敛性和更好的稳健性，而在间断附近，却保持有ENO重构所具有的基本无振荡的特性。早在1996年，Jiang G.S.和Shu C.W在Liu等人研究的基础上提出了三阶和五阶有限差分 WENO重构［9］。本文将致力于把该三阶有限差分WENO重构引入到无网格算法中，发展出一种基于三阶WENO重构的无网格算法。基于无网格点云结构，先通过在点云的每个卫星点方向上引入局部一维坐标系，并结合虚拟点的设置，将有限差分WENO重构中基于一维坐标系的模板构造方法，发展用于无网格点云中的模板构造；对于模板上虚拟点的流场值，则采用一种基于最近节点流场值的插值方法确定。该虚拟点插值方法可利用已有的点云信息，因此避免了直接寻找插值点等耗时的步骤，简化了插值操作；在构造的模板上，采用三阶WENO重构确定算法所涉及的交界面左右状态值；基于上述WENO重构方法，并结合Roe的近似Riemann求解器求得数值通量，对Euler方程进行了求解，编程计算了典型流动算例，验证了所发展的算法获得的数值解能逼近三阶精度。在此基础上，给出了若干绕流算例，展示了所提算法捕捉激波和非定常激波演化等复杂流动问题的能力。

1 无网格空间导数逼近简介

采用无网格算法，流场中不需要网格，只需要有限数量的节点。每一个节点与它周围的节点形成点云。图1给出了一个七点无网格点云。其中i点是中心点，点1～点6是其卫星点。

以函数f为例，在i点的每一个卫星点上，其函数值fk可以用i点处的函数值通过泰勒级数展开得到：

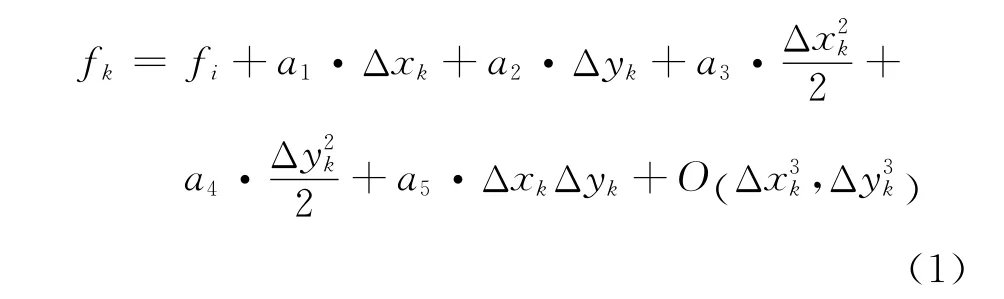
其 中 Δxk＝xk－xi，Δyk＝yk－yi，aj（j＝1，…，5）表示i点处函数f的各阶偏导数，即：

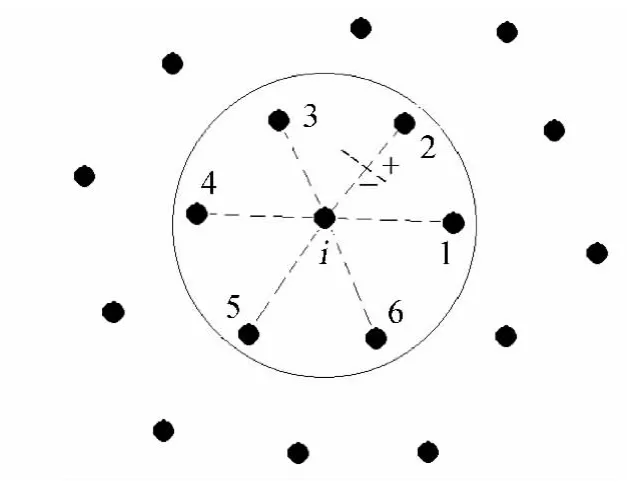
图1 无网格点云Fig.1 Cloud of points for gridless method

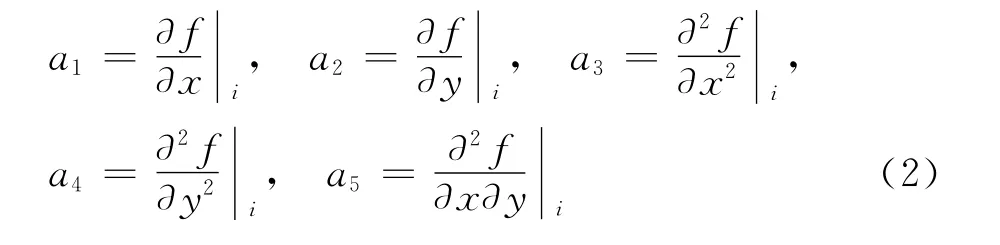
将式（1）保留到二阶项，则得到fk的近似值为：

则aj（j＝1，…，5） 的值可以通过求解如下的最小二乘问题确定：

其中M表示i点的卫星点数。通过式（4）确定aj（j＝1，…，5）的具体过程建议阅读文献［10］的详细描述，这里给出最终的求解方程组：

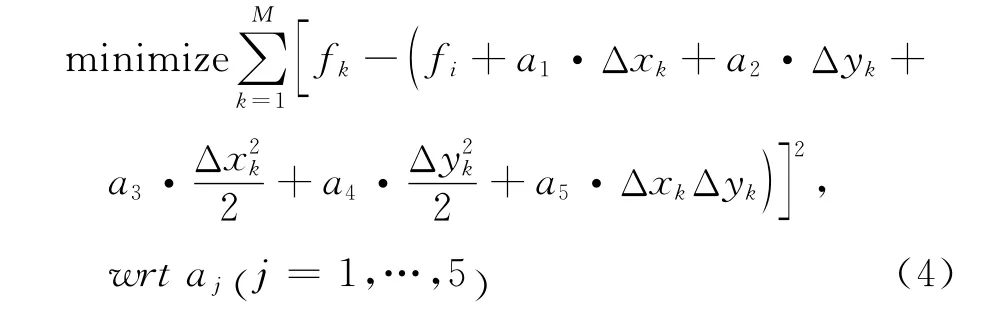
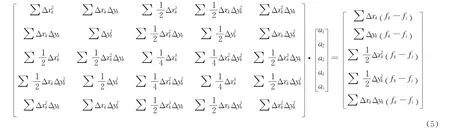
其中∑是 的简写形式。方程组（5）的解可以写成点云中各点函数值的线性组合，即：

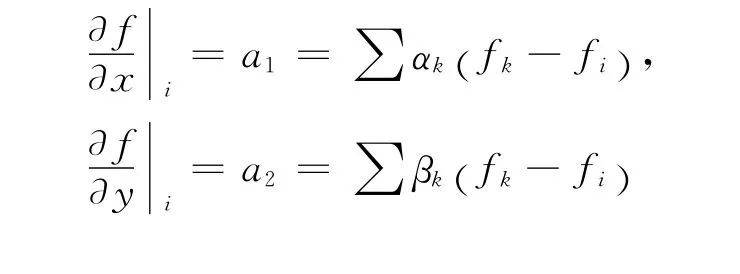
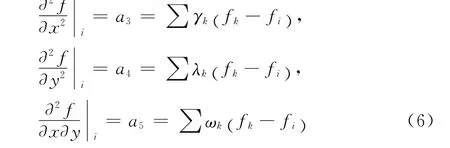
系数αk，βk，γk，λk，ωk由方程组（5）确定。上述各阶偏导数也可以采用中心点与卫星点连线中点处的函数值fik类似求得［10］：

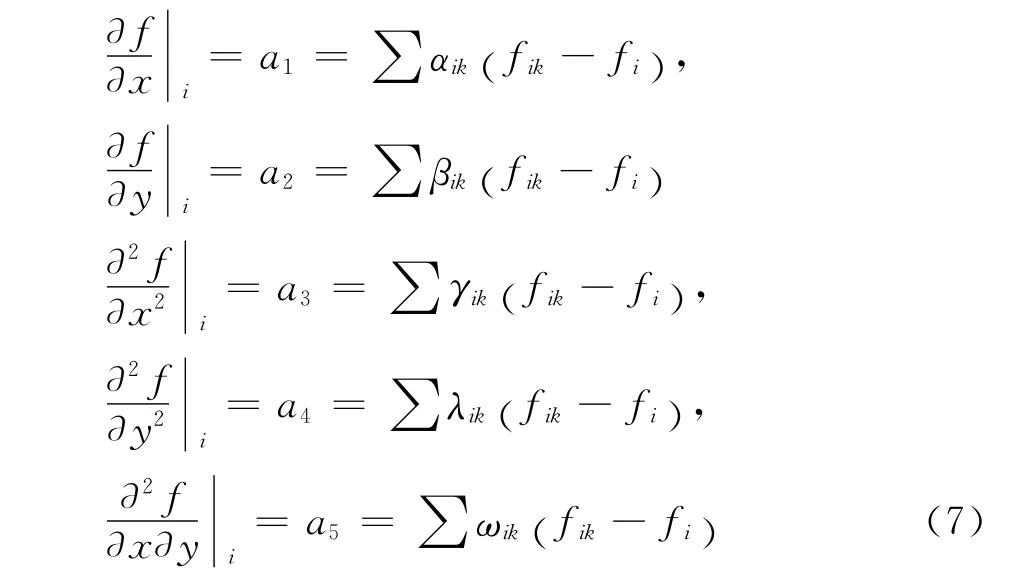
式（7）中的系数αik，βik，γik，λik，ωik与式（6）中的系数αk，βk，γk，λk，ωk有如下关系：

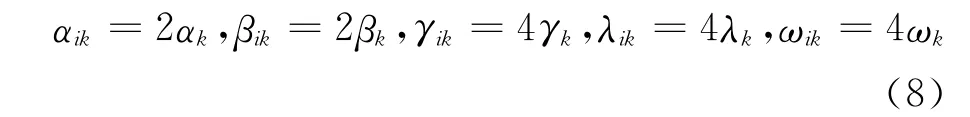
可以看到，这些系数只与点云中各点的几何位置有关，因此可在流场迭代计算前计算储存好。

2 控制方程

本文研究的三阶WENO重构及无网格算法将基于Euler方程展开。在直角坐标系下，守恒形式的Euler方程可写为：

式中，W是守恒矢变量，E和F是对流矢通量，可分别写为：

其中，ρ为密度，u、v为沿坐标x、y上的速度分量，p为气体的压强，e是单位体积内总能。对完全气体满足状态方程

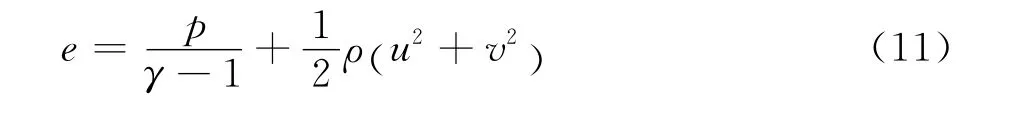
式中，空气的比热比γ＝1.4。

3 基于三阶WENO重构的无网格算法

应用式（7），Euler方程的通量项可近似写为：

Gik是i点和k点连线中点处的数值通量，本文按Roe的近似 Riemann解确定［11］：

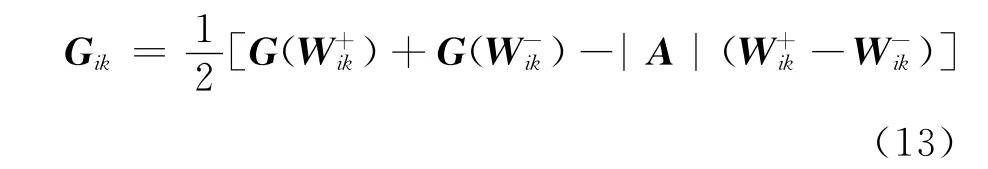
其中A＝是Jacobian矩阵，和是i点和k点连线中点处左右两侧的守恒变量值（见图1中所示）。若采用如下传统的线性逼近重构确定和，则空间精度能达到二阶［2，4］：

其中rik是从i点指向k点的矢量，φ－和φ＋为通量限制器［2］，守恒变量的梯度 ∇Wi在每个点上用式（6）计算给出。

如引言中所述，我们希望空间精度能进一步提高。为此，本文将三阶WENO重构引入到无网格算法中，以替代式（14）的线性逼近重构。下面介绍无网格点云上三阶WENO重构的具体实现方法。

3.1 无网格点云上三阶WENO重构的实现

本文无网格点云上的三阶WENO重构，是基于有限差分 WENO重构发展而来，因此为了叙述方便，我们首先对三阶有限差分WENO重构做一简单的介绍，然后给出在无网格点云上实施三阶WENO重构的过程。

三阶有限差分WENO重构是基于一维坐标系进行的［9］，如图2（a）所示。以函数f为例，每个交界面上左右状态值的重构分别基于由3个节点构成的模板。以i＋1／2处左状态值的重构为例，其重构模板为S＝｛i－1，i，i＋1｝（图2（a）中的红色点），将该模板分成两个子模板S1＝｛i－1，i｝、S2＝｛i，i＋1｝。在这两个子模板上，根据线性分布规律可分别构造i＋1／2处的状态值为：

根据 WENO重构思想［9］，i＋1／2处的左状态值为和的加权和，即：

非线性权系数w1、w2定义为：

其中＝、c＝为优化权系数，ε是为了防止在2光滑流动区域分母为零而加入的一个很小的数，本文取为10－5。Si是模板的光滑度量系数，定义为：

图2 无网格点云上三阶WENO重构模板的构造Fig.2 The stencil of third order WENO reconstruction in a cloud of points

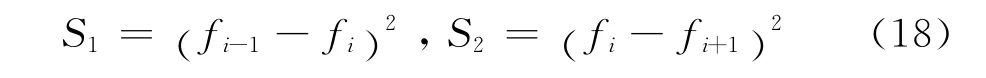
为了将上述有限差分WENO重构发展用于无网格算法，首先需要确定无网格点云上的重构模板。为此，本文基于无网格点云卫星点分布特征，沿点云中心点与卫星点连线方向引入了局部一维坐标系，图2（b）给出了沿k点方向引入的局部一维坐标系。在此局部一维坐标系中，我们在i点的上游方向设置一虚拟点j，并且j点和k点关于i点对称（关于虚拟点上流场值的确定方法将在下一节中介绍）。基于此局部一维坐标系，我们参照有限差分WENO重构方法，采用j点、i点和k点上的值，通过式（16）构造i点和k点连线中点处的左状态值，即：

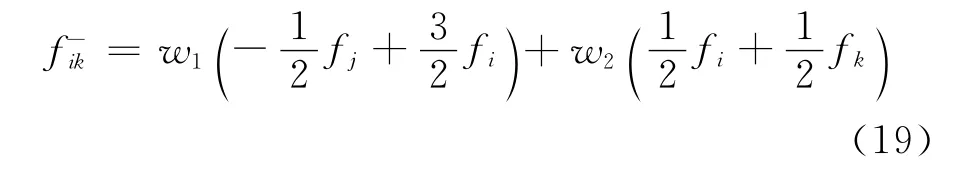
非线性权系数w1、w2也按式（17）计算，此时模板的光滑度量系数相应变为：

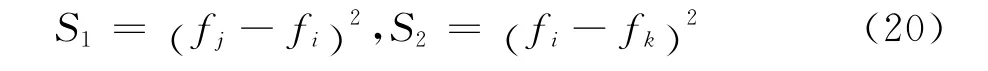
根据对称性，i点和k点连线中点处右状态值可以类似得到：

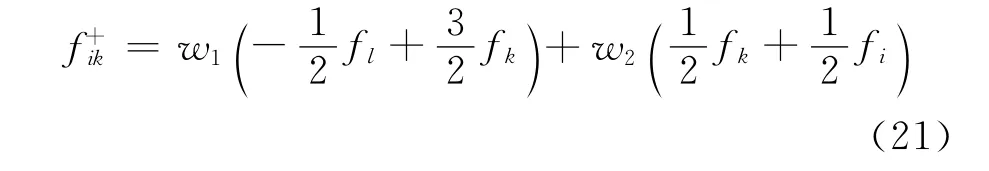
非线性权系数w1、w2也按式（17）计算，此时模板的光滑度量系数相应变为：

式（21）和式（22）中的fl表示上述局部一维坐标系中，i点关于k点的对称点l上的函数值（图2b中没有画出）。

将式（19）和式（21）应用于守恒变量的重构，就可得到中心点和卫星点连线中点处守恒变量的左右状态值。再将左右状态值带入式（13），就可得到每个卫星点方向上的数值通量。

3.2 虚拟点上流场值的确定

在上述WENO重构模板构造过程中我们设置了虚拟点，这些虚拟点上的流场值可以通过插值确定。一种最直接的做法是搜索到虚拟点周围一定范围内的所有节点，作为插值点，然后根据插值方法确定虚拟点上的值。这种做法涉及到逐一搜索插值点的过程，可能需要花费较多的机时，而随后进行的插值系数确定过程，也可能涉及矩阵求逆等操作，同样较为耗时。考虑到对本文采用的无网格算法而言，每个节点的点云结构及求导系数（即式（6）中的系数）本来就已经确定，我们若充分利用这些已有信息，则有望简化插值处理过程。基于此，本文提出了一种基于最近点流场值的插值处理方法。以图2（b）中虚拟点j的流场值确定为例，该插值方法的实施过程如下：

（1）把引入虚拟点j的点云中的节点作为候选点（即图2b中的i点及其卫星点），通过比较与j点的距离，找到这些候选点中距离j点最近的点，为图2（b）中的p点；

（2）虚拟点j上的流场值则可基于p点的流场值，按如下方式逼近：

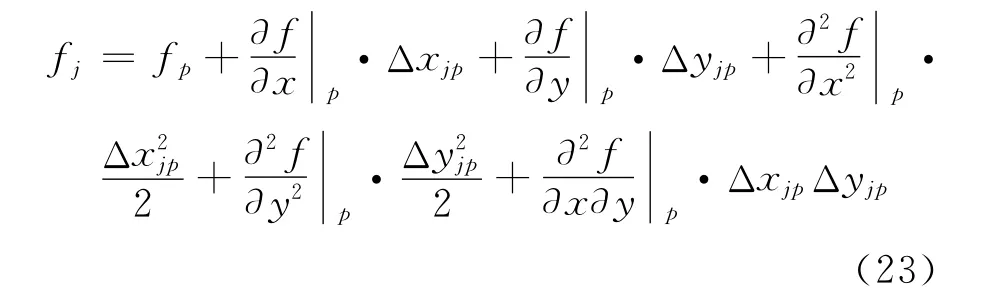
其中Δxjp＝xj－xp，Δyjp＝yj－yp。将各阶偏导数的表达式（6）带入，则式（23）可以进一步写为：

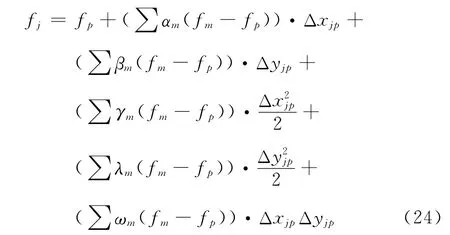
将含有相同函数值的项进行合并，式（24）最终可整理成如下简单形式：

其中Mp表示p点的卫星点总数，各插值系数具体形式为：

可以看到，上述插值方法实质上是直接取p点点云中的节点作为虚拟点j的插值点，因此避免了逐一搜索插值点的过程，节约了计算时间。另外，插值系数也是基于点云已有的求导系数，直接采用式（26）通过简单的代数运算得到，而不需额外引入插值系数，编程实现简单。可以看到，上述插值系数也只与几何量有关，因此同样可以在流场迭代计算前计算存储好。

3.3 时间离散格式

采用上述基于WENO重构的无网格算法离散Euler方程的空间导数后，可以得到方程的半离散形式如下：

其中，Ri为的离散形式。

为了达到空间和时间的一致高阶精度，本文采用Shu C W 和Osher提出的三阶TVD Runge－Kutta时间离散格式［12］：

其中Δt为设定的时间步长。具体求解时还涉及到边界条件的处理，本文对各种边界条件沿用了有限差分WENO重构边界条件的处理方法（如对周期性边界条件通过设置辅助点的方式处理），限于篇幅，不再详细描述，这里列出文献［13］供参考。

4 算例与分析

本文已采用上述基于三阶WENO重构的无网格算法进行了编程，并对典型流动问题进行了计算。这里首先给出求解模型问题典型流动的计算结果，以验证所提算法的精度，在此基础上对存在间断的流动问题进行了数值模拟。

4.1 二维线性模型方程的求解算例

二维线性模型方程的精确解很容易求得，因此常用于检测算法的精度，方程形式及初值如下：

利用特征线法，可求得精确解为u（t，x，y） ＝sin（2π（x＋y－2t））。本文计算区域取为［0，1］×［0，1］，边界条件为周期性边界条件。我们分别采用规则分布的节点（如图3（a））和不规则分布的节点（如图3b）进行了计算。表1为t＝0.2时刻，采用不同密度的规则分布的节点进行的精度分析（表中L1表示所有节点上误差的平均值，L∞表示所有节点上误差的最大值），表2为同一时刻，采用不同密度的不规则分布的节点进行的精度分析。从表1和表2可以看出，采用上述两种布点形式，所发展的无网格算法总体都能逼近三阶精度。图4还给出了采用41×41个规则分布的节点，经过较长时间后t＝2时刻），沿y＝0.5解的分布，作为比较，还同时给出了基于线性逼近重构的计算结果。可以看到，基于三阶WENO重构的计算结果与精确解符合更好，在极值点附近也没有观察到明显耗散。

图3 两种不同的布点形式Fig.3 Two different types of point distribution

表1 二维线性模型方程的精度分析（采用规则分布的点）Table 1 Accuracy of 2Dlinear equation（regular point distribution）

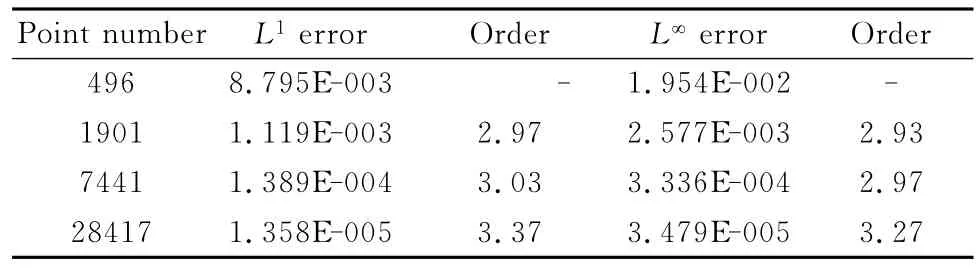
表2 二维线性模型方程的精度分析（采用不规则分布的点）Table 2 Accuracy of 2Dlinear equation（irregular point distribution）

图4 基于线性逼近重构与基于WENO重构得到的y＝0.5位置解的分布（t＝2）Fig.4 Comparison of results using linear reconstruction and WENO reconstruction along y＝0.5at t＝2

4.2 二维Euler方程的求解算例

4.2.1 等熵涡问题

本节采用所发展的无网格算法求解二维等熵涡问题，以检测算法求解Euler方程的精度。设初始的平均流为 （ρ，u，v，p）＝ （1 ，1 ，1，1），在平均流 上 加入一个等熵涡：

其中r2＝（x－5）2＋（y－5）2，ε＝5，该问题的精确解是等熵涡随平均流等速移动。本文计算区域取［0，10］×［0，10］，边界条件取周期性边界条件。与前一算例一样，我们分别采用规则分布的节点和不规则分布的节点进行了计算（这两种节点分布形式类似于图3，限于篇幅，这里不再展示）。表3和表4分别给出了t＝2时刻，采用不同密度的规则分布的节点和不规则分布的节点进行的精度分析。可以看出，无论是采用规则分布的节点还是不规则分布的节点，所发展的无网格算法总体都能逼近三阶精度。图5还给出了采用81×81个规则分布的节点计算出的t＝20时刻沿y＝5流体密度的分布，作为比较，还同时给出了基于线性逼近重构的计算结果。可以看到，基于三阶WENO重构得到的结果与精确值符合更好，特别是在极值点附近也没有观察到明显的耗散。

表3 二维Euler方程的精度分析（采用规则分布的点）Table 3 Accuracy of 2DEuler equations（regular point distribution）

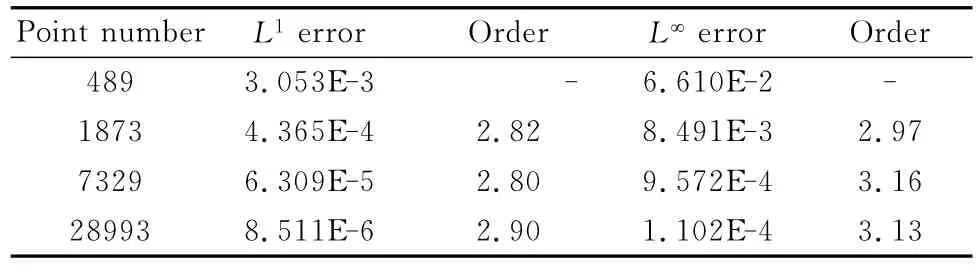
表4 二维Euler方程的精度分析（采用不规则分布的点）Table 4 Accuracy of 2DEuler equations（irregular point distribution）

图5 基于线性逼近重构与基于WENO重构得到的y＝5位置的密度分布（t＝20）Fig.5 Comparison of results using linear reconstruction and WENO reconstruction along y＝5at t＝20

4.2.2 激波管流动问题

激波管流动问题常用于检测算法对激波，接触间断等的捕捉能力。本算例计算区域为［0 ，1］×［0 ，0 .1］的矩形区域，其中布置了76090个不规则分布的节点。初始条件设置为［14］：

本文分别采用基于线性逼近重构和三阶WENO重构的无网格算法进行了计算，算至时刻t＝0.0039。图6为流体密度在激波和接触间断附近的计算结果，图7则为对应的在膨胀波附近的计算结果。整体上，基于三阶WENO重构的无网格算法捕捉的激波、接触间断和膨胀波较线性逼近重构更靠近精确值，与文献［14］五阶有限差分 WENO重构（x方向点的间距与本文的相同）结果接近（见图6、图7），且在膨胀波附近也没有明显的振荡，体现出WENO重构 “基本无振荡”的特性（见图7）。

图6 激波和接触间断附近的密度分布Fig.6 Density distribution near shock and contact discontinuity

图7 膨胀波附近的密度分布Fig.7 Density distribution near expansion wave

4.2.3 超声速半圆柱绕流

考虑马赫数为3的超声速半圆柱绕流，圆柱半径为r＝0.5。基于图8的计算区域，布置了101×61个规则分布的节点。外边界采用自由来流条件，物面采用无穿透条件，上下出流边界采用外推法处理［15］，图8分别给出了无网格算法基于线性逼近重构以及WENO重构的压强等值线，图中可看出，两种方法都捕捉到了脱体弓形激波，激波距驻点的距离都为0.68r（这与文献［15］计算出的距离吻合），但基于WENO重构的无网格算法捕捉的激波更加清晰，表明后者三阶WENO重构具有更高的分辨率。图9给出了无网格算法基于线性逼近重构以及WENO重构的收敛曲线，整体看来，两种方法的收敛曲线比较接近。另外，我们还对计算时间进行了统计，两种方法迭代5000步所需的时间分别为197s和203s（CPU为Intel Core I7－860）。这一结果展示出基于WENO重构的无网格算法在计算效率上能与传统基于线性逼近重构的无网格算法相当。

4.2.4 激波过弯道绕双圆柱流场

在前面算例对发展的基于WENO重构的无网格算法进行验证的基础上，本节将该算法应用于求解激波过弯道绕双圆柱流场，以展示其处理含非定常激波演化的复杂流动问题的效果。该算例几何外形取自文［16］的实验模型，本文计算捕捉到与实验类似的波系演化结构，这里只给出计算结果。

图8 计算得到的压强等值线Fig.8 Comparison of the pressure contours obtained

图9 收敛曲线Fig.9 Convergence history

图10为本算例的计算区域及采用的节点分布（节点总数为31972个）。初始时刻，在弯道上方入口处有一马赫数为1.8的激波，随着流动的发展，该激波逐渐沿弯道移动，并与双圆柱发生碰撞。图11（a～f）给出了六个典型时刻的密度等值线。可以看到，当与第一个圆柱相遇时，激波从物面上反射，进一步会出现激波与激波的相互作用，出现马赫杆、接触间断等流动现象。激波继续向下游移动，在遇到第二个圆柱时又发生反射，同时，前后圆柱间的激波发生多次相撞，使得流场变得非常复杂，但本文计算出的结果给出了清晰的流场结构，展示了所发展的算法处理含非定常激波演化流动的能力，有望发展用于实际的复杂流动数值模拟。

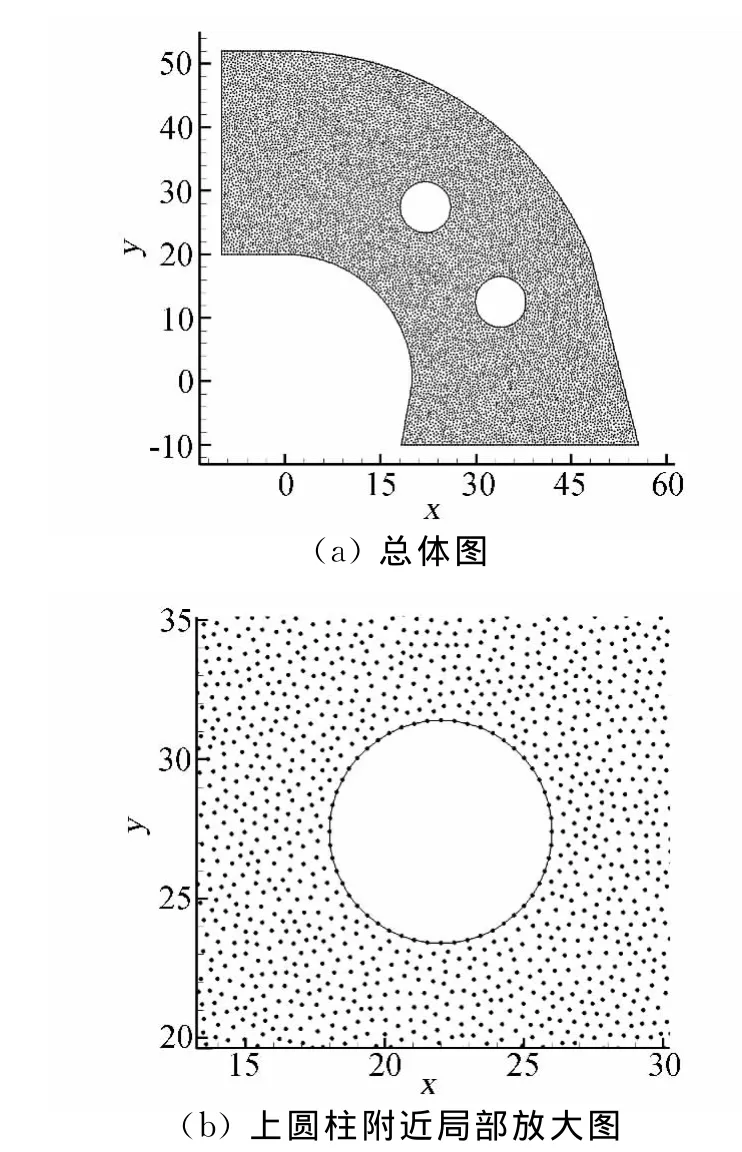
图10 激波过弯道绕双圆柱流场计算区域及节点分布Fig.10 Point distribution for simulating the flow field of shock wave through curved channel around double cylinders

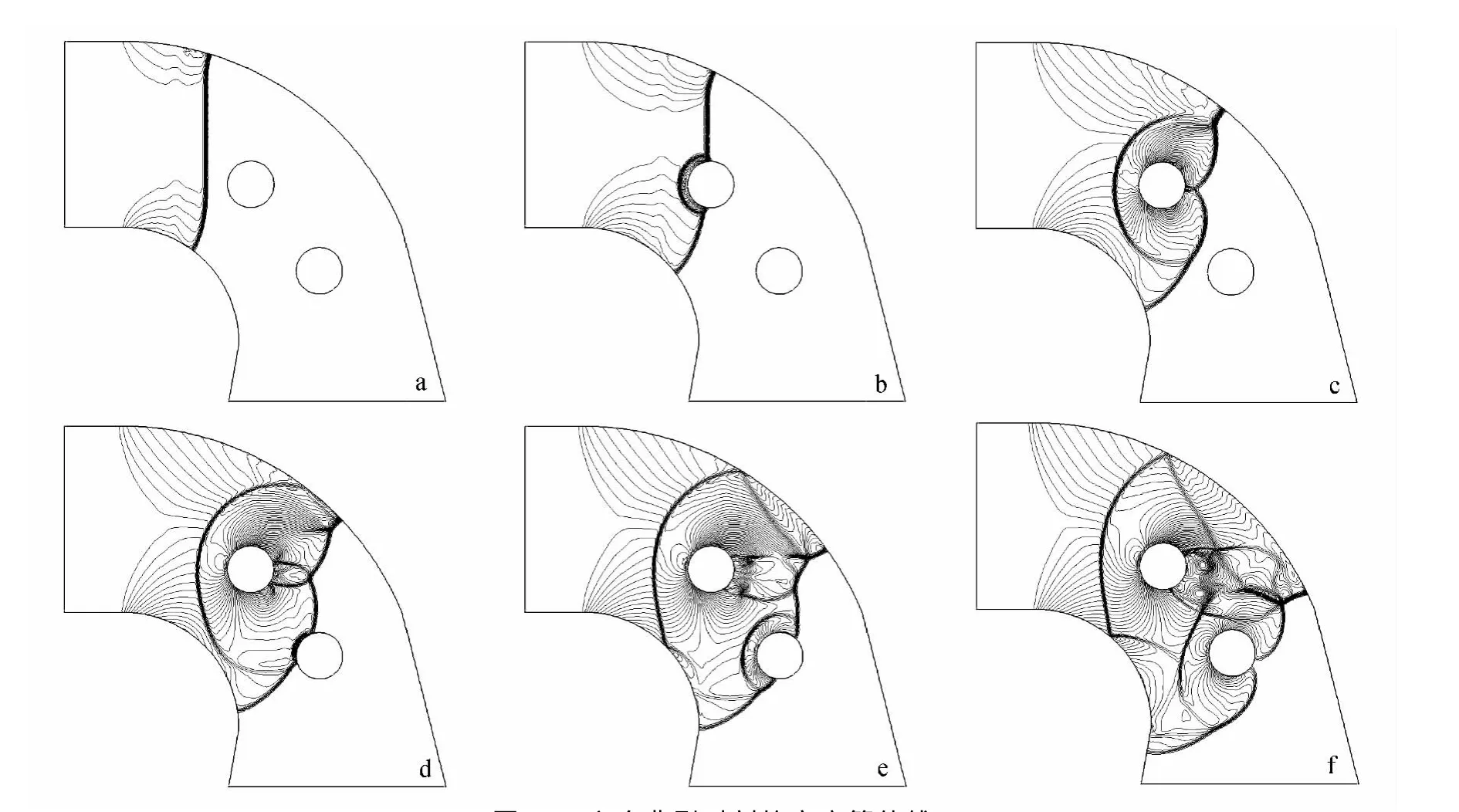
图11 六个典型时刻的密度等值线Fig.11 Density contours of the flow field at six typical times

5 结 论

本文通过在无网格算法中引入WENO重构，发展了基于三阶WENO重构的无网格算法。算例验证了该算法获得的数值解如预期能逼近三阶精度；与传统的基于线性逼近重构的无网格算法相比，在相同的布点情况下，本文算法捕捉的激波等间断问题具有更高分辨率，能体现出WENO重构“基本无振荡”的特性。由于算法只需无网格布点，不但适合处理激波管等简单外形流动问题，也适合处理存在多个物体相互干扰的复杂流动问题。

［1］BATINA J T.A gridless Euler／Navier－Stokes solution algorithm for complex aircraft applications［R］.AIAA 93－0333.

［2］MORINISHI K.Gridless type solution for high Reynolds number multielement flow fields［R］.AIAA 95－1856.

［3］CHEN H Q.An implicit gridless method and its applications［J］.ACTAAerodynamicaSinica，2002，20（2）：133－140.（in Chinese）陈红全.隐式无网格算法及其应用研究［J］.空气动力学学报，2002，20（2）：133－140.

［4］SRIDAR D，BALAKRISHNAN N.An upwind finite difference scheme for meshless solvers［J］.JournalofComputational Physics，2003，189：1－29.

［5］SHENG M J，YE Z Y，JIANG C Q.Study of the boundary layer solution coupled with gridless method［J］.ChineseJournal ofComputationalMechanics，2011，28（6）：290－925.（in Chinese）盛鸣剑，叶正寅，蒋超奇.附面层修正应用于无网格算法的研究［J］.计算力学学报，2011，28（6）：290－925.

［6］MA Z H.Research of adaptive meshfree and hybridized mesh／meshfree methods［D］.Nanjing：Nanjing University of Aeronautics and Astronautics，2008.（in Chinese）马志华.自适应无网格及网格和无网格混合算法研究［D］.南京：南京航空航天大学，2008.

［7］LU X D，OSHER S，CHAN T.Weighted essentially non－oscillatory schemes［J］.JournalofComputationalPhysics，1994，115（1）：200－212.

［8］HARTEN A，ENGQUIST B，OSHER S，et al.Uniformly high－order accurate essentially non－oscillatory shock－capturing schemes［J］.JournalofComputationalPhysics，1987，71（2）：231－303.

［9］JIANG G S，SHU C W.Efficient implementation of weighted ENO schemes［J］.JournalofComputationalPhysics，1996，126（1）：202－228.

［10］MA Z H，CHEN H Q，ZHOU C H.A study of point moving adaptivity in gridless method［J］.Computermethodsinapplied mechanicsandengineering，2008，197：1926－1937.

［11］ROE P L.Approximate Riemann solvers，parameter vectors，and difference schemes［J］.JournalofComputationalPhysics，1981，23：357－372.

［12］SHU C W，STANLEY OSHER.Efficient implementation of essentially non－oscillatory shock capturing schemes［J］.Journal ofComputationalPhysics，1988，77（2）：439－471.

［13］SHU C W.Essentially non－oscillatory and weighted essentially non－oscillatory schemes for hyperbolic conservation laws［R］.NACA／CR－97－206253，1－78.

［14］YANG S P，LI S F，QU X M，et al.Numerical comparison of fifth－order WENO schemes and second－order Godunov schemes［J］.NaturalScienceJournalofXiangtanUniversity，2006，28（2）：8－12.（in Chinese）杨水平，李寿佛，屈小妹，等.五阶FD－WENO格式和二阶Godunov格式MUSCL的数值测试与定量比较［J］.湘潭大学自然科学学报，2006，28（2）：8－12.

［15］SJOGREEN B.High order centered difference methods for the compressible Navier－Stokes equations［J］.JournalofComputationalPhysics，1995，117（1）：67－78.

［16］YE Xichao，LE Jialing，YANG Hui.Flow field of shock wave through curved channel around double cylinder［J］.AerodynamicExperimentAndMeasurement＆Control，1996，10（2）：80－85.