DSMC热化学模拟分子数对氮氧离解反应计算影响的分析
杨浩森,张 斌,刘 洪,陈 方
(上海交通大学 航空航天学院,上海 200240)
0 引 言
直接模拟蒙特卡洛法(DSMC)的基本原理是采用有限个模拟分子代替真实气体分子,直接模拟微观态的气体分子运动和碰撞,是一种更接近于气体真实的运动状态和能量交换的模拟方法。鉴于这种直接的物理模型,与基于连续介质假设的CFD方法相比,DSMC在模拟稀薄流区流动和涉及热化学非平衡的流动时具有天然的优势。
由于DSMC以统计学为基础,则作为流场统计母体的模拟分子数量对流场最后的统计结果将产生直接的影响。这种直接的影响主要表现在计算效率和计算精度两个方面。概括来讲,就是在保证计算精度的同时尽量减少流场中使用的模拟分子数以降低计算开销。
对于不涉及热化学非平衡现象的流场,流场中模拟分子的主要行为是相互碰撞以实现速度的重新分布,这种行为只涉及分子平动动能,物理模型相对简单。Bird和Alexander等人对此类流动中模拟分子数对DSMC计算的影响做了定性分析,建议每个流场网格单元中布置15-25个模拟分子以得到合理的流场计算结果[1-3],该研究结论作为此类流场模拟的推荐值被广泛使用,Pei-Yuan Tzeng等人在此基础上以Rayleigh-Bénard流动为例分析了模拟分子数对流场涡结构准确性的影响[4]。2009年,Bird对全新的DSMC07程序中网格模拟分子数做了更为准确全面地分析,得出从1维到3维流场理论计算“改进因子”与网格模拟分子数的关系,结果表明在2维不含热化学非平衡流场的DSMC计算中,相同网格模拟分子数对计算的改进效果并不会因为流场物理条件的不同而不同。结合计算效率,Bird建议,在二维不含热化学非平衡的流场模拟中网格模拟分子数应该在20-30个,此结论与流场物理条件无关[5]。
上述讨论仅仅局限在不涉及热化学非平衡的流场模拟中。但是,在研究例如高超声速飞行器和飞行器再入等问题时,流场中会出现显著的热化学非平衡的现象,这类现象对流场特征有十分重要的影响[6-7]。与传统方法不同,DSMC在模拟此类非平衡现象时,要求模拟分子除了实现弹性碰撞之外,还要准确模拟分子内能的激发与松弛过程。概括而言,与普通流场中DSMC主要考虑平动能不同,模拟分子的碰撞行为将同时涉及平动,转动和振动三种能量的相互传递。对于此类更加复杂的流场模拟,物理条件对分子内能的影响是显著的,要求在不同的物理状态下(主要是温度),碰撞模拟应该符合不同的能量松弛规律,不能如普通流场一概视之[8]。
本文使用DSMC模拟了空气中最易发生化学反应的三种氮氧分子:氮气,氧气和一氧化氮在热浴条件下的离解反应,并以此来研究在涉及热化学非平衡的流场中模拟分子数对计算结果的影响。并从分子能态分布和能量松弛等方面分析了这种影响产生的内在原因。
1 DSMC热化学非平衡模拟方法
1.1 概述
根据分子动力学和化学动力学的基本原理,DSMC模拟热化学非平衡主要分为两个部分:热力学能量传递和各类化学反应[9]。这两个过程均通过模拟分子之间的碰撞实现。在不涉及热化学非平衡流场的计算中,模拟分子主要携带分子平动能,而与普通流场计算中的模拟分子相比,模拟热化学非平衡流场要求每一个模拟分子具有相应的内能能态,具体如下式所示:

普通流场模拟分子与非平衡流场模拟分子的主要区别如表1所示。与普通流场不同,流场的非平衡现象主要就来源于分子的内能能态的激发与松弛过程,对于平动能的传能而言,一般情况下可以用弹性碰撞表示,而将涉及分子内能传递的碰撞归入非弹性碰撞类。

表1 模拟分子特性比较Table 1 Different between normal and nonequilibrium simulation molecules
上述所有的能量形式都存在相互独立的能量松弛时间,在不考虑分子电离的情况下,三种主要的能量形式:平动能(Transitional Energy),转动能(Rotational Energy)和振动能(Vibrational Energy)所对应的松弛时间存在如下关系:

松弛时间的倒数被定义为松弛碰撞数,用以描述单位时间内单个分子相应能量松弛所需要的碰撞次数。一般而言,平动能只需要单次碰撞便可以实现松弛过程,即分子速度重新分布,此类碰撞模型相对简单,而且平动能松弛与实际的物理条件无关。而其他两种分子内能能态却相对比较复杂,在不同的流场温度下,内能松弛需要的时间是不同的[6],亦即松弛碰撞数是不同的。因此,DSMC在不同的流场状态下准确模拟内能松弛碰撞是影响流场终态准确性的关键因素。
在进行分子各能态能量之间的相互有效传递之后,再根据碰撞总能和各类化学反应的相应特征判定化学反应的进行。
1.2 DSMC模拟离解反应
到目前为止,被广泛使用的标准DSMC化学反应能量模型是Bird所提出的TCE(Total Collision Energy)模型[10]。在这个模型中,离解气体分子的离解反应是由分子振动能主导的,根据Bird的TCE模型,对一个特定的分子碰撞对而言,碰撞能量分为分子平动动能,转动能和振动能。在分子对碰撞的过程中,按照Larsen-Borgnakke模型进行各自由度之间的能量传递和再分配,最后的平衡态能量分布根据Boltzmann平衡分布给出[11-12]。
在DSMC模拟化学反应的过程中,模拟分子之间的非弹性碰撞会导致分子各自由度能量的重新分配,根据化学反应的细致平衡原理[9],分子内能(转动能和振动能)在分子相对平动能的直接激发下对化学反应做出相应的贡献。而对于离解反应而言,由于上述能量之间的转化,导致分子振动量子态从低能态向高能态跃迁,当分子振动能态超出特定的离解能级时,才发生离解反应[13]。本文分子振动能级分布采用式(3)所示的非简谐振子模型,其中,相关的能级参数如表2所示。
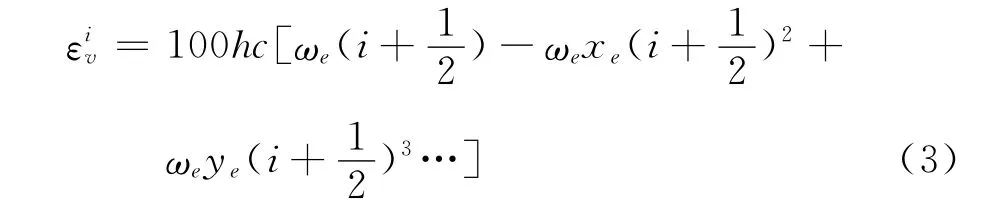

表2 振动能级参数[14]Table 2 Parameters in vibrational energy model
对于离解反应的模拟,一个重要的考量标准就是不同温度下的平衡离解度α(Degree of Dissociation-DOD),它描述了在不同的平衡温度下,某一类分子离解的程度,即离解原子质量分数。根据Bird和Hansen(1976)提供的数据[12],这里不加推导的给出氮气、氧气和一氧化氮在不同温度下的平衡离解度公式为:

2 计算结果及分析
2.1 DSMC程序验证
首先对DSMC程序模拟三种氮氧分子离解反应的正确性进行验证。以标准状态(1个大气压,0摄氏度)分子数密度为准,为提高计算效率,采用一个封闭系统的热浴反应来模拟三种气体在不同平衡温度下的离解反应。根据统计学原理,随机系统的统计涨落仅依赖于总的模拟分子数,而与模拟分子的布置无关[15],故将整个计算域视为一个网格,网格模拟分子数为7000个。全文DSMC程序参数如表3所示。

表3 本文全局算例计算参数Table 3 Global calculation parameters of DSMC
图1所示的结果为本文使用的DSMC计算程序在表3中列举的不同分子数密度下对三种氮氧分子进行热浴的模拟结果。氮气的模拟平衡温度范围大致为5000K~16000K,氧气大致为2600K~9000K,一氧化氮大致为3000K~11000K,图例中n0=2.686×1023。由于分子的离解度与计算域的温度直接相关,所以本文选择简单绝热热浴问题进行计算模拟,以尽可能多的排除其他影响因素从而突出模拟分子数的影响。
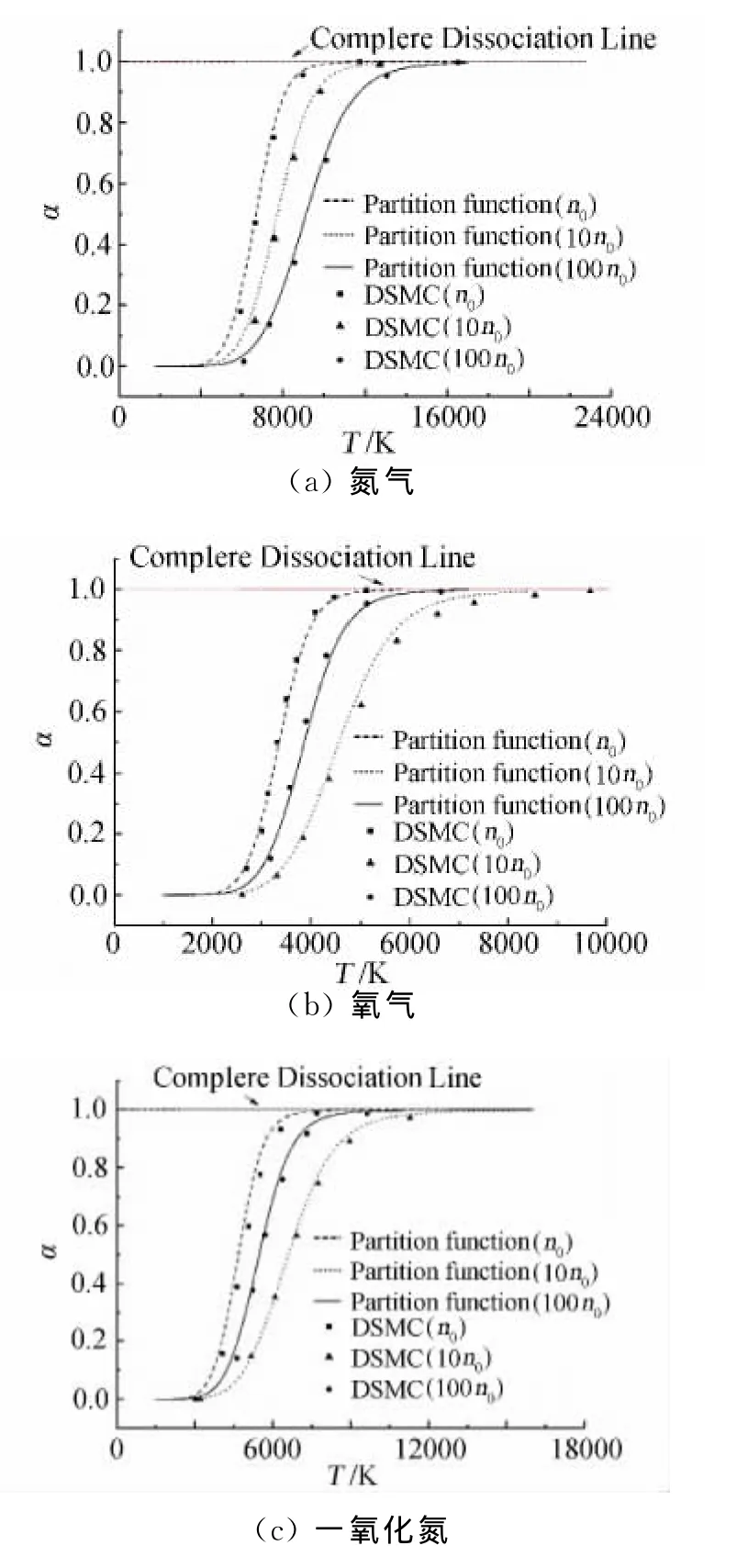
图1 DSMC模拟氧气和氮气离解度曲线Fig.1 DSMC result of degree of dissociation
从图1可以看出,由于三种分子化学键键能不同,则离解特征温度存在差异。其中氮气最为稳定,整个离解温度范围最高;氧气最易离解,而一氧化氮正好介于氮气和氧气之间。DSMC模拟结果在不同的分子数密度下和理论值符合得比较好,表明程序是可靠的。
进一步分析之前,分别对每一种气体选择一个标准算例作为判断模拟分子数对计算结果影响的标定。计算条件为:分子数密度为标准状态下的分子数密度,模拟分子数为4000。图2为氧气,氮气和一氧化氮标准算例的计算结果和理论值的误差基本在10%以内(图中误差限为5%)。

图2 标准算例结果Fig.2 DSMC results of the standard examples
在图2所示的标准算例中,与高温高离解度的情况相比,低温低离解度下DSMC模拟结果与理论值之间的误差较大(计算结果显示最大误差达到了12%左右),其原因根据Gallis和Harvey的研究结果[16],空气中气体的化学反应并非由振动能唯一控制,在分子振动能还没有被高度激发的状态下,平动能和转动能对化学反应的影响将变得不可忽略,本文使用的DSMC程序模拟化学反应是基于分子振动能的控制,故在低温下模拟误差较大。
2.2 模拟分子数对DSMC模拟结果的影响
图3给出了在和标准算例相同的计算条件下,不同的模拟分子数在不同的平衡离解度下模拟的误差(图中的虚线表示上一节规定的相应离解度下标准算例计算结果与理论值之间的误差,以此作为计算结果被接受的标定值)。
图3中标识出了在不同的平衡离解度下需要的模拟分子数下限,超过这个阈值之后,计算精度并没有得到明显的提升,但是由于模拟分子数增多带来的计算开销却会相应增大。综合该离解度下的流场平衡温度,总结得到的模拟粒子数需求如表4所示。
考虑到DSMC的统计误差,故表3给出的分子数阈值以一个小范围给出。很明显,随着温度的升高,氮氧分子离解度上升,此时要求的模拟分子数也随之升高。离解度为95%时要求的初始模拟分子数是5%离解度时的10倍左右,这一结果与Bird早期提出的对普通流场DSMC模拟分子数选取的统一建议标准不同。本文结果表明,化学反应系统要求的模拟分子数根据物理条件不同应当作区别对待。
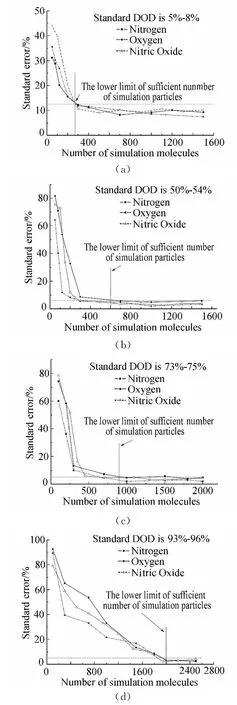
图3 不同模拟分子数下离解度误差Fig.3 Degree of disassociation error with different simulation molecules

表4 不同理论离解度下需要的模拟分子数Table 4 The effective number of simulation molecules in different DOD
(1)不同模拟分子数对分子能级分布的影响
根据Bird的理论,在计算稳定之后,流场中的分子振动能级分布将满足Boltzmann平衡分布,在理论离解度为75%的情况下三种氮氧气体使用不同的模拟分子数最后流场分子达到的状态如图4所示。

图4 三种分子在不同模拟分子数下的计算平衡能级分布Fig.4 Equilibrium energy distribution in different simulation molecules
根据上一节离解误差的结论,理论离解度为75%时要求模拟分子数为900个。图4显示的结果表明,在使用900个模拟分子的情况下,最后DSMC分子能级抽样统计结果和Boltzmann平衡分布一致。而在模拟分子数为150时,最后的分子能级分布偏离Boltzmann分布较远,这一结果主要由两个因素所致:其一,从统计学的角度出发,母体样本数太少,导致的抽样不准确;其二,初始模拟分子数不足,导致分子碰撞传能不够充分,导致流场能量分布发生偏倚,这一点将在下一节做详细讨论。
(2)不同模拟分子数对有效碰撞率和振动松弛碰撞率的影响
分子之间的能量传递是通过分子对之间的碰撞实现的,根据Parker的理论[17],在不同温度下,分子振动能的松弛需要满足不同的松弛碰撞数(即分子的振动能要完全松弛要求发生的平均碰撞次数),且在特定的温度下,振动松弛碰撞数大致为一个确定值,温度越高需要的松弛碰撞数越少。根据这个理论,本文定义了以下两个考察参数,分别为:“有效碰撞率”(Effective Collision Rate)和“振动松弛碰撞率”(Vibrational Relaxation Collision Rate)。从模拟离解反应的角度出发,在DSMC模拟过程中,将有双原子分子参与的碰撞定义为“有效碰撞(NCmoleculeinvolved)”,而“有效碰撞率(νeffective)”描述的是“有效碰撞”占总碰撞数(NCtotal)的比例。“振动松弛碰撞率(νvib)”则描述在“有效碰撞”中,发生能量松弛过程的碰撞数(NCvibrelax)比例,具体表述如下:

图5给出了在平衡离解度分别为30%和75%两种情况下三中氮氧分子碰撞传能情况。从图中可以明显看出,分子有效碰撞率和分子振动松弛碰撞率随着模拟分子数的增加,最后都各自趋于一个稳定值,理论离解度为30%时大致稳定的模拟分子数为300个,离解度75%时大致稳定的模拟分子数为900个,这个结果和上文的结论一致。
模拟分子数过少,离解不足,流场中剩余的双原子分子数量较多,此时有效碰撞率较高,另一方面,松弛分子碰撞对抽样不足,不能达到足够的松弛碰撞数,即振动松弛碰撞率较低。随着模拟分子数的增加,计算离解度升高,此时剩余双原子分子数量减少,则有效碰撞率下降。随着模拟分子数的增加松弛碰撞抽样增加,松弛碰撞率增大直至稳定。这种趋势表明,同一平衡状态下,正确模拟的平衡碰撞率跟模拟分子数量无关,为一恒定值。这个结果与Parker的理论一致。
考虑极端的情况,在气体几乎完全离解的情况下,由于单原子并不具有内部自由度,亦即不具有转动和振动等内能能态,从统计学的角度,如果离解度过高且没有足够的分子(双原子分子)为程序提供建立平衡状态所需要的采样母体的规模,就会直接导致流场能量统计失准,最直接的结果就是流场温度的统计值不准确。所以就要求起始时刻有足够多的模拟分子基数,这样,随着离解反应的进行,也能够有足够的未离解分子供程序进行采样统计从而得出正确的流场状态,而随着模拟的进行,流场逐渐趋近稳定状态,这时即便是分子完全离解也不会影响最后的模拟结果。
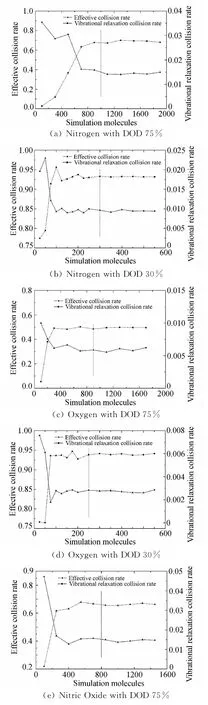
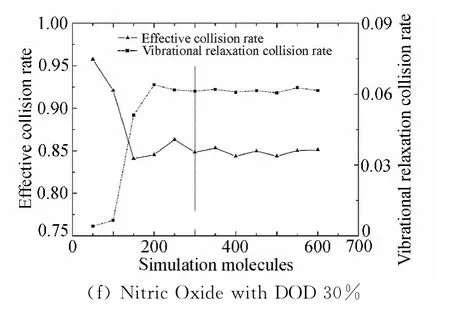
图5 不同模拟分子数下分子碰撞率Fig.5 Molecule collision rate in different number of simulation molecules
3 结 论
本文选取空气中化学反应最常见的三种氮氧类分子,使用DSMC对三种气体在绝热热浴条件下进行了离解反应模拟。离解度模拟结果显示,对含有化学反应的流场,DSMC模拟随着流场温度和气体分子离解度的升高,正确模拟这一化学过程所要求的模拟分子数同样呈上升趋势,在本文的计算条件下,以氮气为例,从离解度5%到离解度95%得到正确结果的模拟分子数阈值分别为250、550、850和1900,最高离解度与最低离解度模拟分子数阈值相差10倍左右。这一规律与Bird对普通流场DSMC模拟建议的统一20~30个模拟分子数不同,在含有化学反应的流场计算中,准确模拟要求的模拟分子数阈值与温度(离解度)呈正相关,超出阈值之后,计算开销增大,但是并不会给计算精度带来明显的变化。这一结果表明,在不同的流场物理条件下,DSMC要求的模拟分子数具有特异性,不能一概而论。
由于文中的讨论是在绝热封闭条件下进行的,所以在模拟的过程中,不会有新分子的加入。从理论上讲,在真实流动的条件下,由于流场中会有新分子的流入,所以需要的网格模拟分子数会比表4列出的模拟分子数下限要少。但是,对于不同温度下模拟分子数需求的规律是一致的,所以,本文得到的结论对于含有化学非平衡现象的流场模拟具有一定的参考价值。
[1]WU Q F,CHEN W F,et al.Rarefied gas dynamics[M].National University of Defense Technology Publishing,2004.(In chinese)吴其芬,陈伟芳,等.稀薄气体动力学[M].湖南:国防科技大学出版社,2004.
[2]ALEXANDER F J,GARCIA A L,ALDER B J.Cell size dependence of transport coefficients in stochastic particle algorithms[J].Phys.Fluids,1998,10(6):1540-1542.
[3]BIRD G A.The direct simulation Monte Carlo method:current status and perspectives[A].in:M.Mareschal(Ed.),Microscopic Simulations of Complex Flows,Plenum[M],New York,1990.
[4]TZENG Pei-Yuan,LIU Ming-Ho.Influence of number of simulated particles on DSMC modeling of micro-scale Rayleigh-Be′nard flows[J].InternationalJournalofHeatandMassTransfer,2005,45:2841-2855.
[5]BIRD G A,GALLIS M A,et al.Accuracy and efficiency of the sophisticated direct simulation Monte Carlo algorithm for simulating noncontinuum gas flows[J].PhysicsofFluids,2009,21:017103.
[6]BOYD I D.Rotational and vibrational nonequilibrium effects in rarefied hypersonic flows[J].JournalofThermophysicsand HeatTransfer.1990,4:478-484.
[7]DAAN Frenkel,BEREND Smit.Understanding molecular simulation:from algorithms to applications[M].Academic Press,New York,2010.
[8]WU Q F,CHEN W F,et al.The DSMC method for the thermochemical nonequilibrium flows of high temperature rarefied gas[M].National University of Defense Technology Publishing,1999.(In chinese)吴其芬,陈伟芳.高温稀薄气体热化学非平衡流动的DSMC方法[M].湖南:国防科技大学出版,1999.
[9]GOLDSWORTHY M J,MACROSSAN M N,ABDEL-JAWAD M M.Nonequilibrium reaction rates in the macroscopic chemistry method for direct simulation Monte Carlo calculations[J].PhysicsofFluids,2007,19:066101.
[10]BORGNAKKE C,LARSEN P S.Statistical collision model for Monte Carlo simulation of polyatomic gas mixture[J].Journal ofComputationalPhysics,1975,18:405-420.
[11]BIRD G A.Molecular gas dynamics and the direct simulation of gas flows[M].Clarendon Press,Oxford,1994.
[12]BOYD I.Nonequilibrium chemistry modeling in rarefied hypersonic flows[A].AIAA Thermophysics Conference[C],33rd,Norfolk,VA;United State;28June-1July 1999.
[13]HERZBERG G.Molecular spectra and molecular structure Vol.spectra of diatomic molecules[M].Princeton,1950.
[14]MALVIN H Kalos,PAULA A Whitlock.Mont Carlo method second,revised and enlarged edition[M].Wiley,New York,2008.
[15]MICHAEL A Gallis,JOHN K Harvey.The modeling of chemical reactions and thermochemical nonequilibrium in particle simulation computations[J].PhysicsofFluids,1998,10(6):1344-1358.
[16]PARKER G J.Rotational and vibrational relaxation in diatomic gases[J].Phys.Fluids,1959,2(4):449-62.

