实时线性考试的设计理念及实施

孟汇涓

近些年来，项目反应理论（Item Response Theory，IRT）逐渐为国内的考试主办方所了解，并被应用于一些测试中。与经典测试理论（Classical Test Theory，CTT）相比，IRT理论的核心优势是：（1）对题目参数的计算不依赖于参试的考生群体；（2）对考生分数的计算不依赖于试卷中使用的题目。在这样的理论构架下，在IRT几个假设（单维性、局部独立性和单调性）可以基本保证的前提下，施以合理的数据采集方法，历年考试题目的参数可以被放在同一个尺度上，而由这些题目所组成的不同试卷不再需要额外的等值步骤就可以保证试卷之间由题目参数算出的IRT分数的可比性（Kolen&Brennan，2004，p.175）[1]。

IRT题目参数以及IRT分数的这种特性，在计算机考试平台的辅助下，使考试主办方不再局限于以往的固定试卷模式，开始使用以题库形式为发送基础的各种灵活的设计，如计算机自适应考试（Computerized Adaptive Test，CAT）或实时线性考试（Linear On-the-Fly Test，LOFT）。这里的题库是指考试主办方拥有的所有试题中的一部分，可以用来组成几套甚至十几套的试卷。我国测量界的学者如张厚粲、漆书青、戴海崎、丁树良等自20世纪80年代末90年代初就开始了对CAT的研究（张厚粲，1990；江西师大“题库理论”组，1987）[2][3]；相比之下，实时线性考试是一个较为陌生的概念，也是这篇文章所要具体阐述的。

1 LOFT的设计理念

1.1 什么是LOFT?

从LOFT的名称来看，首先这是一个线性考试（Linear）：计算机依次将试卷中的题目发送给考生，而不是根据考生对先前试题回答的结果从题库中一一抽取题目。所以，LOFT不是“量体裁衣”、“因人选题”的计算机自适应考试，也不是传统的固定试卷，需要事先组好，通过命题组审核，并且收到相同固定试卷的考生回答同样的试题。

其次，考试是实时的（On-the-Fly）：组卷工作是考生坐在计算机前的那一瞬间启动，由计算机驱动程序按照事先制订好的内容和统计方面的组卷规则，从一个比较大的题库里自动抽题组卷，发送给考生。因为抽题过程中的随机算法的调控，考生拿到的试题或多或少总有不同。

总之，LOFT综合了CAT和固定试卷设计的一些特点，如前者的对题库的使用以及由计算机抽选试题；后者的对试卷内容统计方面高度一致的要求。

1.2 LOFT的优点

首先，与固定试卷相比，LOFT考试安全性比较高。因为考生拿到的试卷上的题目多有不同，它可以降低考试结束后考生互相对题而产生的潜在漏题风险。同时，LOFT设计性价比更好，因为发布①Peason VUE考试发布（Test Publishing）的工作内容是：将客户提供的试题、试卷结构（包括考试大纲的要求、试题数量等）和考试设计（是使用固定试卷、CAT还是LOFT）输入软件，然后将考试用QTI（Question and Test Interoperability）的形式输出，上传到VUE的考试发送系统。一个LOFT题库和发布一套固定试卷的费用是一样的。考试主办方如果需要屏蔽几个试题，可以直接在题库上操作，不像固定试卷，必须要重新发布，从而减少了因为屏蔽试题而增加的相关费用。

和CAT相比，LOFT题库中试题的使用更加均衡。如果LOFT和CAT使用同一个题库，LOFT不会像CAT一样，出现难度适中、区分度大的试题被反复抽选，而过难的试题或简单题使用频率过低的情况，从而降低了信息量大的试题因频繁曝光而被泄露的潜在风险。

其次，LOFT对题库的要求比CAT要低。在试题数量方面，如果是固定长度（fixed-length）的CAT，题库中需要有大约12份相同长度、相同质量且没有重叠的的试题（Stocking，1994）[4]；而LOFT题库中的试题数量要求没有CAT那么高（Kingsbury，Bontempo，Zara，2009）[5]，在美国教育考试服务中心（ETS）的一篇研究报告中，LOFT的题库试题数量是固定试卷长度的5倍即可满足要求（Stocking，Smith，&Swanson，2000）[6]。在试题难度分布方面，CAT因为要根据考生答题的情况和计算出的IRT分数选题，它通常要求每一个考试内容的试题难度都要和考生能力分布相吻合，才能发挥出CAT的优势，而LOFT只需要各部分内容的试题数量比例均衡，对每个内容的试题难度没有更多要求，从而很大程度上减轻了考试主办方发展题库的负担。

LOFT的第三个优势是它允许考生略过一些比较难的题目，回头再做；而在CAT中，考生必须顺序回答每一个试题，答完后不可以检查更改。显而易见，LOFT提供了考生比较熟悉的一种应试状态。

最后，选择考试设计需要考虑考试的目的及效率。如果某项考试仅仅是决定考生通过与否，考试主办方只需要在分数线附近实现对成绩的准确测量即可。如果LOFT统计指标设计好的话，可以和CAT一样满足这个目的（Becker，Bontempo，Dickison，Masters，2010）[7]，这样的话就可以放弃对题库有很高要求的CAT，使用LOFT来降低考试的成本。像资格认证这一类的考试，LOFT比CAT可能更为合适。

综上所述，使用LOFT题库的考试设计一般来说要比固定试卷在考试安全性上更有保障；在满足考试目的的前提下，LOFT可以比CAT更好地平衡题库中试题的使用频率，降低漏题风险；同时，在LOFT的设计下，考生可以检查做过的试题，更改答案，减轻考生在CAT中可能会产生的考试焦虑。最后，如果题库还在建设之中，无法满足CAT设计对试题难度分布的要求，采用LOFT不失为一个比固定试卷更加灵活有效、经济实惠的过渡方案。

2 LOFT的实施

LOFT由两部分组成，一是题库，包括实测题库和预测题库；二是组卷规则，包括内容方面和统计方面的规则。在实测题库中，所有算分的题目都需要有参数，如IRT下的题目参数，它们被用来计算并衡量计算机组出的试卷是否达到事先设定的统计目标，所以这些试题都是以往考试中的题目。而预测题库中的试题则是新题，考生对它们的回答只是用来评估试题质量，获取题目参数，并不计入成绩。国外很多大规模考试项目都是通过预测题来发展题库，保证考试良性运行。

以下通过一个虚拟的考试案例（见表1）来介绍实施LOFT每个环节的操作步骤。这个案例中的考试试题在内容上的分布并没有达到应用LOFT设计的理想状态，却也是很多考试主办方在实际工作中可能需要面对的现实情况。

2.1 组建预测题库

设计预测题库的第一步是根据考生人数及使用的测量理论模型估计出预测题的数量。如表1中的考试，预测题目的数据点共有40 000个（4 000人×10道预测题），因为校准题目参数的人数要求设在400人，可以算出这个考试预测题库的题目数量应为100道题（40 000/400）。

第二步，考试主办方需要对已有试题进行分析，找出题库中最欠缺的内容领域，以决定预测题库中试题的分布。用表1中试题总量和考试大纲规定题数，可以算出目前每个内容领域下可以不重叠地组几套试卷。通过这个分析可以发现内容1、2和5，试题数量明显少于其他内容，所以预测试题就分布在这3个内容。表2是试题分析结果，由此决定试卷及题库中预测题的分布，以及考试后各部分试题数量会有怎样的增长。考试主办方需要通过这样的分析和规划，尽量均衡地将考试中各内容领域下试题数量的比例逐渐拉齐，使题库中实测题使用频率趋于一致，从而最大程度地实现使用LOFT这种设计的优势。

表1 虚拟考试案例

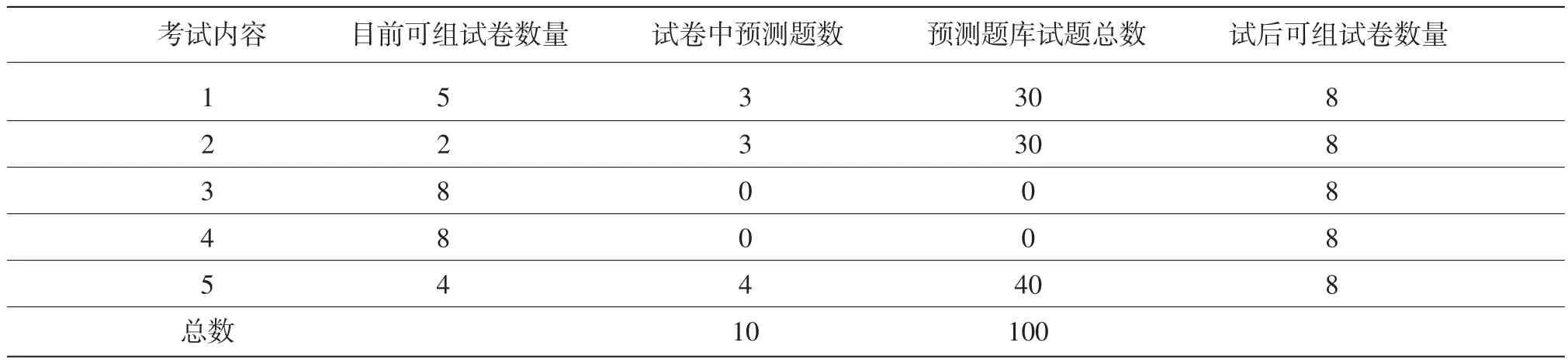
表2 预测试题及题库规划

2.2 组建实测题库

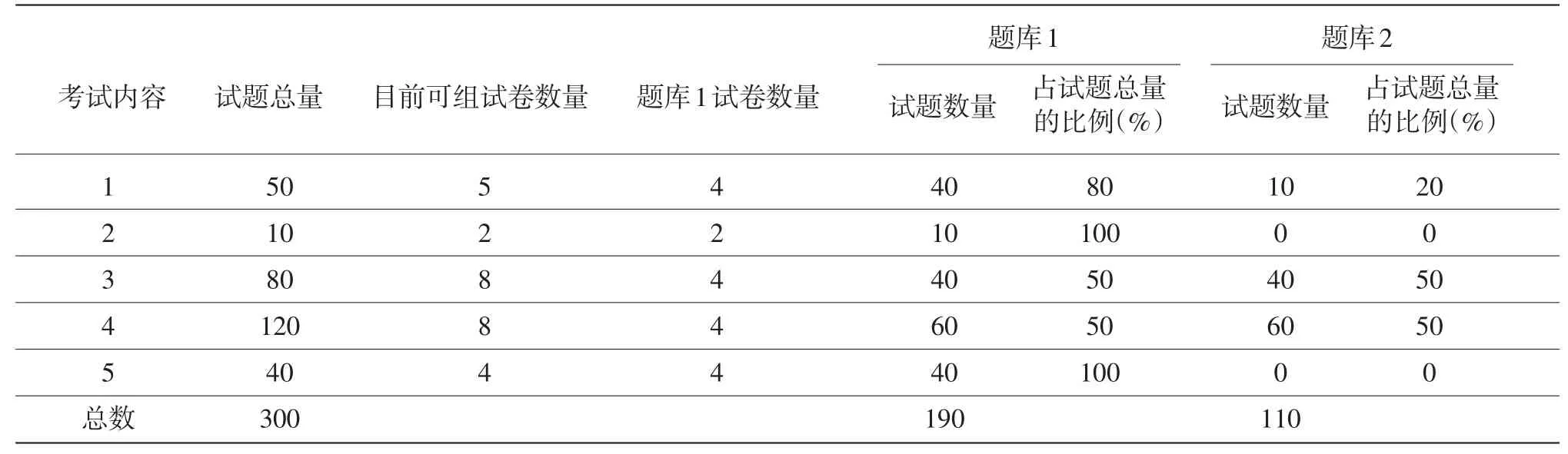
表3 实测题库规划

在LOFT设计下，通常不会把考试主办方手中所有的有题目参数的实测题一次性全部用完，所以，就像组固定试卷一样，也需要组建一个在考试时使用的题库，尽可能地平衡试题的使用频率，保证不同年度不同题库下所组建的LOFT试卷质量的一致性。

信息采集模块界面主要包括机床列表对车间设备状态进行总览，如图5所示，可以实现对机床状态监控、数据库连接管理、机床管理、各机床实时数据监控等功能。机床列表界面对机床编号、IP地址、名称、加工状态、急停状态、报警状态进行实时监控显示。

组建实测题库有三个步骤：第一步，要确定每一个考试内容应该有多少道题，它基本上是由考试主办方对试题平均曝光率的要求和目前可组试卷数量决定的。如在这个虚拟考试案例中，假设试题平均曝光率设为25%，那就意味着题库中需要放4套试卷的题量，就是200道题。如果实际情况如表3所示，内容1、2和5试题数量较少，所以关于这3个内容的实测题大部分甚至是全部放在了第一个题库中，从而使试题平均曝光率不至于过高。而试题充足的内容3和4，因为设定了上限，就不会出现同一内容下题目太多，试题曝光率过低的情况。需要注意的一点是，在这个例子中，内容1、2、和5的试题可能需要重复使用，在下一次考试时放在题库2里。当然，如果像2.1中描述的，所有的预测题都集中在这些内容上，本次考试结束后，通过审查的预测题会进入题库，改善题库2的现状。

第二步，拆分敌对题。敌对题是指两类题：一类是克隆题，如题干和选项文字不变，只是数字发生变化；第二类是暗示题，就是某道题中的内容有助于考生回答其他试题。通常情况下，敌对题不允许出现在同一张试卷上。因为不管是哪一种敌对题，考生如果幸运，就会一下子做对两三道题；反之，就会连着出错。这两种情况都会影响考生成绩的准确性和有效性，降低考试的公平性。

一般来说，考试发展一段时间后，题库中就会存在敌对题，有的是一对，两道题互相敌对；有的是一组，有几道甚至十几道互为敌对题。如果一组中的敌对题同时出现在题库中，这些试题的曝光率就会高于那些没有敌对题关系的试题。举例来说，5道题，没有敌对题时，每道题被随机抽中的概率是20%；如果其中两道题是敌对题，实际抽选的时候就只有4道题可用，每道题被抽中的概率就是25%，两道敌对题各有12.5%的抽中概率。显然，敌对题的曝光率很低，非敌对题的曝光率升高，降低使用LOFT的好处。所以，拆分敌对题是保证题库中试题被均衡使用的重要步骤之一。

敌对题基本是按照题库题数比例来拆分的，见表4。假如一组中两道敌对题属于内容3，因为题库1试题数量占总量的比例是50%，就可以把其中的一道放在题库1里，另一道放在题库2里。这样这两道敌对题就不会互相影响，也不会对这个内容中其他试题的曝光率造成影响。

第三步，平衡题库试题难度。这里的难度，是指题库中所有试题IRT难度参数的平均值。考试主办方不能把所有的难题，或者所有的简单题，或者所有难度适中的试题都放在一个题库里，如果这样做，使用第二个题库时，就很难保证LOFT试卷质量前后的一致性。表5显示，通过这一步骤，题库1和题库2总体难度基本一致，而且每个考试内容下的试题平均难度也非常相似。

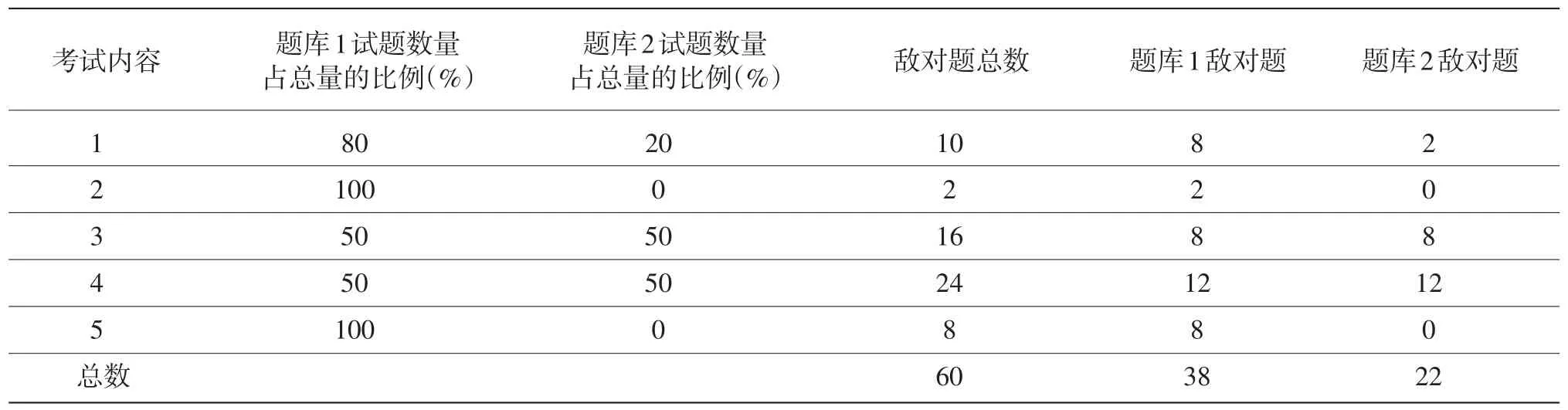
表4 敌对题的拆分

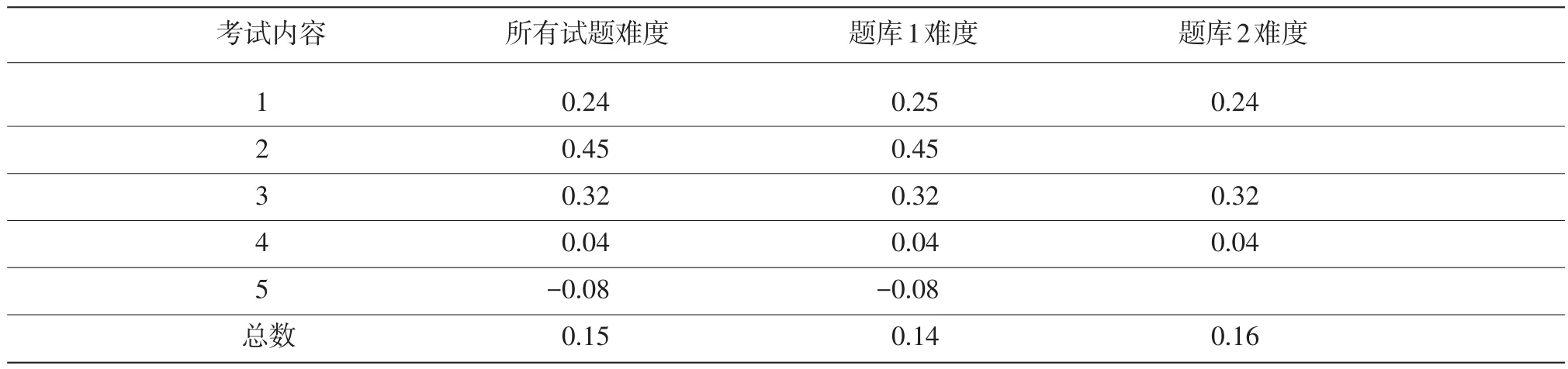
表5 平衡题库难度

2.3 计算组卷规则

LOFT设计下的另一个组成部分是组卷规则，主要目的是实现试卷在内容和统计方面的等值。

首先是内容方面的规则。如果考试大纲在每个内容领域下又列举了更具体的考查点，就需要考试主办方进一步设定各考查点的试题比例，以保证同一个考试中不同LOFT试卷在内容方面上的一致性。举例来说明，如果这个虚拟考试案例第一部分的内容是数学，下面有两个考查点：解析几何和矩阵计算。如果只规定数学考10道题，计算机有可能给考生甲抽8道几何题、2道矩阵题，给考生乙8道矩阵题和2道几何题。这种内容方面的不均衡显然会造成考试的不公平。当然，也并不是每个考查点都一定需要有抽题的数量规则，它由几个因素决定：（1）考试大纲要求的试题数量。如果一个考试内容总共就考两三道题，就没有设定考查点的题目数量的必要性。（2）题库中各考查点的试题数量占其考查内容试题数量的比例。以虚拟考试的第2个内容为例（见表6），根据考试大纲，这部分需要5道题。假设第2个考试内容有5个考查点ABCDE，题库中关于考查点A有6道题，BCDE各有一道题，共有10道题，A考查点的试题数量占第2个考查内容试题总量的3/5（6/10）。如果题库中第2个考试内容没有敌对题（表6中情境1），按照比例规则，应该在关于2A考查点的试题里抽3道，在BCDE里共抽2道。在这种情况下，组卷规则中不需要指定除了2A以外的考查点的试题数量。（3）决定考查点组卷规则时还需要考虑敌对题的数量。如果2A考查点有两组敌对题，每组两道（表6中情境2），那么选题时，2A实际上只有4道题供选择，这时抽题规则就不应是上面所说的“2A里抽3道”，而是在2A里抽2～3题，在BCDE里抽2～3题。这种考虑，在敌对题数量比较多时尤其重要。如果忽略这个因素，设定的规则就有可能无法运行，或者影响试题曝光率的均衡性。

考查点的抽题规则可以是固定的题数，也可以是由最小值和最大值组成的题数范围。设定范围的好处是计算机组卷的灵活度比较大；而且，一旦考试主办方因为内容方面的原因需要屏蔽一些试题，这些规则更容易保持其合理性，减少重新发布题库的次数。

总之，只有把这些因素全部考虑进去，才能保证LOFT内容方面抽题规则的准确性和可行性。而这些规则保证了LOFT试卷在内容方面的均衡，使每个考生拿到的题目都能够全面覆盖考试大纲，确保考试内容方面的有效性。

LOFT设计下的另一部分组卷规则是统计方面的。在IRT理论下，比较常见的试卷统计指标有考试信息（Test Information）、考试特征（Test Characteristic）和单参数模型下的考试难度（试题难度参数的平均值）。在这个虚拟考试案例中使用的是考试信息，见表7。一条规则设在划界分数，theta=0。虽然在理论上来说，如果是决定考生通过与否，只要保证划界分数附近的成绩被准确测量就已经达到考试目的。在实际设计中，另有两条规则分别设在theta分数-1和+1，也就是划界分数加1、减1，来保证LOFT试卷的信息曲线在更大分数范围内的一致性。在这里，划界分数那一点的信息量设得最大，从而使测量误差尽可能减少，而两边的分数-1和+1，要求的信息量相对要低。

考试信息目标的设定要合理，不能一味地抬高数值区间。比如说IRTRasch模型下的试题信息量最高值是0.25，50道题的试卷在某个theta点上可能达到的最多信息量是12.5（0.25×50）。如果将目标定为12.5或略低一点，可能连一套符合统计规则的LOFT试卷也组不出来。较为可行的方法是参考在转为LOFT设计之前使用的固定试卷在不同theta分数上的信息量，然后进行适量调整。调整时可以根据题库题目的具体情况，将划界分数这个点上的LOFT考试信息量设定的略高于固定试卷，这样会减少考试误差，从而提高考试在区分考生时的准确度和稳定度。设定比较高、比较严格的统计指标，也是在LOFT中提升考试质量的一个重要途径。

表6 考查点的抽题规则

表7 虚拟考试案例的LOFT试卷统计规则

最后，对于这三个分数点，没有规定一个固定的信息值，而是限定了一个很窄的区间，因为如果设定的统计目标为一个固定的信息值，计算机组卷灵活度较小，会延长组卷时间；同时，有些题被选择的频率可能会高出其他试题，这也违背了使用LOFT设计的初衷。

3 LOFT的评估

在发送实时线性考试之前，考试主办方需要对计算机根据题库及组卷规则组出的几百套甚至上千套LOFT试卷进行方方面面的评估。

第一，试题曝光率，就是一道题目有多大比例被考生看到。例如1000套试卷，如果有1道题出现在200套试卷中，它的曝光率就是20%（200/1000）。题库中试题曝光率是不同的，某些考试内容试题数量多，每道题的曝光率就会比较小；反之，某些内容试题数量很少，每道题的曝光率就会高。另外，如果一道题的敌对题很多，它的试题曝光率会明显低于题库中其他试题。如果试题曝光率的分布和预期的有很大差异，考试主办方应该查看具体试题及组卷规则，找出原因，做相应调整。

第二，试卷重叠率，就是同一个考试的不同试卷，两两相比，试题相同的比例。与试题曝光率一样，如果题库或组卷规则有问题，试卷重叠率也会出现异常。同时，这个指标可以帮助考试主办方直接了解，在一个考场的两个考生在考试结束后，如果互相讨论试题，试题完全一样的现象有多严重。当然，因为是机考，能把考试时间和地点都安排在一起的概率本身就要打折扣，再加上试题顺序的变化，相识考生之间能对上的试题数量可能比计算出来的要低。

第三，试卷难度的差异，可以用每套试卷试题IRT难度参数的平均值作为指标。虽然拿到不同试卷的考生最终成绩会通过IRT等值全部拉齐，但试卷之间的难度差别越小，对考生的考试体验影响越小，考试公平就越容易得到保证。

第四，试卷的信息量，通过计算所有LOFT试卷在不同IRT分数上信息量的最大值和最小值，可以画出LOFT试卷考试信息曲线区间图（见图1）。图1显示的是，1000套LOFT试卷，不论考生收到哪一套，在每个IRT分数点上的考试信息量都会在这个窄窄的区间范围之内。这样的分析可以帮助我们直观地了解不同LOFT试卷考试信息曲线之间的差异度，进一步确定LOFT设计的合理性。

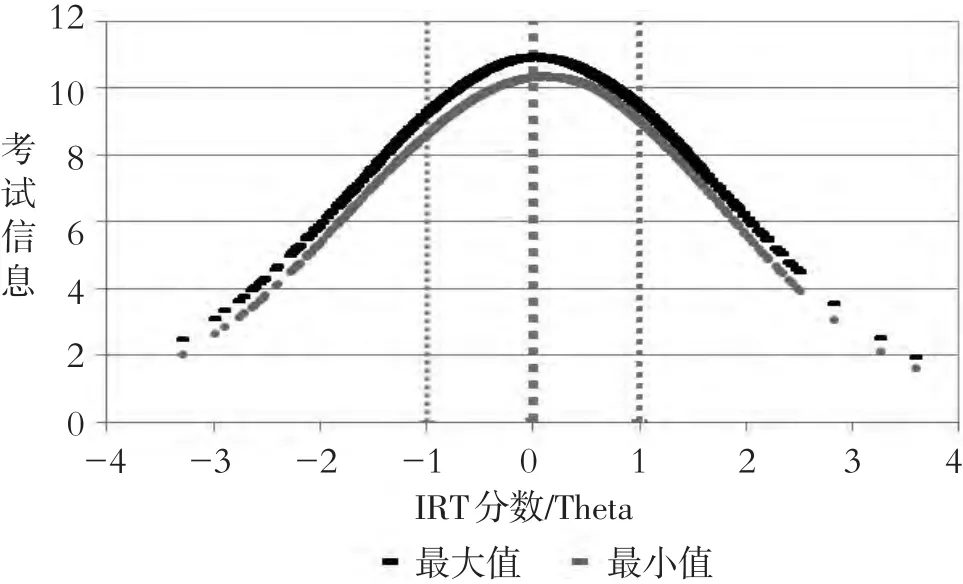
图1 1000套LOFT试卷考试信息曲线区间

以上就是针对一个考试的虚拟案例，考试主办方实施LOFT设计时需要操作的具体环节。显而易见，比起固定试卷，它对题目数量以及考试驱动程序的要求更高，设计起来更为复杂。同时，因为省略了人工审查试卷的步骤，命题人员对敌对题的判断务必要准确，设定组卷规则的工作也会变得比较繁琐，评估LOFT试卷的工作相对费时费力，这些都是考试主办方在决定使用LOFT设计之前需要考虑的问题。当然，它特有的优势仍然可以使它成为最为适合的考试设计方案，满足考试目的，保证考试公平。（感谢Pearson VUE 的Susan Steinkamp，Brad Wu和Xinrui Wang对本文内容的讨论和建议！）

[1]Kolen，M.J.，&Brennan，R.L..Test equating，scaling，and linking:Methods and practices（2nd ed.）[M].New York:Springer-Verlag，2004.

[2]张厚粲.心理测量学的新方向——计算机化适应性测验[M]//自学考试研究论文集（第二集）.北京：经济科学出版社，1990.

[3]江西师大“题库理论”组.考生智能水平的自适应测验[J].江西师范大学学报，1987（2）.

[4]Stocking，M.L..Three practical issues for modern adaptive testing item pools[C]//ETSResearch Report No.94-5.Educational Testing Service，Princeton，NJ.1994.

[5]Kingsbury，G.G.，Bontempo，B.，&Zara R..A Comparison of CAT with LOFT Methods for Certification Examinations[C]//Paper presented at National Organization for Competency Assurance Annual Educational Conference.Phoenix，Arizona.2009.

[6]Stocking，M.L.，Smith，R.，&Swanson，L..An Investigation of Approaches to Computerizing the GRERSubject Tests[C]//ETS Research Report No.00-4.Educational Testing Service，Princeton，NJ.2000.

[7]Becker，K.A.，Bontempo，B.，Dickison，P.，&Masters，J.S..A comparison of CAT and LOFT for a growing item bank[C]//Paper presented at the annual meeting of the International Association for Computer Adaptive Testing.Arnhem，NL.2010.