两种DIF检测方法的模拟研究
廖虹宇 王立君
1 引言
考试作为一种相对公平竞争的机制,从古至今都是人才选拔的主要方式。现代社会不管是升学、就业升职等都离不开考试,考试的重要性日益凸显。那么考试项目本身是否足够公平?考试内容是否有利于某些群体,而对另外的群体不利呢?同时,在考试公平性受到影响时,考试的效度也得不到保证。现代考试采用项目功能差异(Differential Item Functioning,DIF)来研究该问题。DIF分析作为评估测验公平性和效度的关键,已经成为世界标准化考试质量分析的必要环节。由于DIF研究的重要性,曾秀芹和孟庆茂(1998,1999)等较早在国内进行了DIF的相关研究,随后严芳和张增修(2001),任杰(2002),曹亦薇(2003)张颖和赵世明(2004),鹿士义(2004),刘文、边玉芳和陈玲丽(2010)等将DIF分析运用到了各种测验的分析当中,可见国内越来越多的研究者开始重视DIF分析在测验质量评估中的作用。另外,关于DIF方法的比较也涌现出一些文章,如董圣鸿和马世晔(2001),于媛颖(2004),骆方和张厚粲(2006)。但是这些研究都是基于实际数据的研究,由于实际数据的特殊性,用其作为研究的基础,难以对不同方法间的特性差异得出普遍的结论。而Monte Carlo模拟作为一种经济高效的方法可以为我们提供更为普遍的结论。因此,本研究采用Monte Carlo模拟,对两种常用的DIF分析方法进行比较。
目前,已经开发出了许多DIF检测方法,如MH方法(Mantel-Haenszel Procedure),SIBTEST方法(Simultaneous Item Bias Procedure),LR方法(Logistic Regression Procedure),STND 方法(Standardization),Lord卡方检验法等。各种方法都有其优缺点,在此本文选取MH和LR方法,两种方法均使用普遍,且检出率高。MH方法计算简单,花费低,易于实际应用,且不要求大样本(Narayanan&Swaminathan,1996)。LR方法可以看作MH方法的扩展方法,可同时有效地检测一致性DIF(Uniform DIF)和非一致性DIF(Nonuniform DIF)(Rogers&Swaminathan,1993)。
2 两种DIF检测方法的介绍
2.1 MH方法
MH方法由Mantel和Haenszel(1959)首先提出,Holland(1985)以及Holland和Thayer(1988)把这种方法用于检测项目功能差异[3]。现在已经成为检测DIF应用最为广泛的一种方法。MH法用于侦查两级记分项目的DIF,以测验总分作为匹配变量。MH方法统计量的计算建立在一张S×2×2的列联表中,其中S是测验总分的水平数,对于其中的任一水平K,可构成一个来自两子群体在项目上得、失分数的2×2列联次数表(见表1)。

表1 MH法S×2×2列联表
根据样本数据完成上述的S×2×2列联表,即可按表中数据计算αMH,公式如下:

其中f1rk、f0rk分别是在第k个能力水平组中,参照组答对项目的人数和答错项目的人数;f1fk、f0fk则是目标组答对的人数和答错的人数。
αMH的取值介于0至正无穷之间。αMH=1.0时,表示该研究项目无DIF;αMH<1.0时,表示研究项目对目标组有较低难度;αMH>1.0时,表示所研究项目对参照组有较低难度。但是由于αMH的计算来自样本数据,因此对其值是否等于1.0必须进行统计检验(董圣鸿,马世晔,2001)。
2.2 LR方法
Swaminathan和Rogers于1990年介绍了此方法:令Y为项目分数变量,取值为1或0;令Z为观察变量,通常为测验总分;令V为被试分类变量。在完全的Logistic回归模型中,在给定Z与V的条件下,被试正确作答该测验项目的概率为:

对上式两边取对数,整理得:
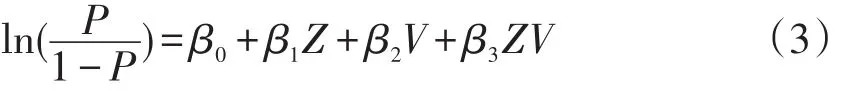
这样就将Logistic回归模型转化成了线性回归模型,因变量就是我们通常所说的Logit,Z和V都是观察变量,ZV项仅是一个记号,表示两观察变量的组合水平。虽非直接观察变量,但也可由Z与V的观察变量而推定。用极大似然法或最小二乘法等其他方法估出回归参数β0、β1、β2和β3。对于这些估计的回归参数可以用假设检验方法检验它们的显著性。检验的不同结果,对DIF的检测有不同的含义:如果方程中只有β0与β1不为零(与零有显著差异),则表示该项目无DIF;如果方程中β0、β1与β2均不为零,表示该项目有一致性DIF;如果ZV项参数β3也不为零,则表示项目存在非一致性DIF](鹿士义,2004)。
3 实验设计
3.1 数据模拟
本研究所使用的是两参数Logistic模型,对于任意一个能力为θ的被试,其在项目i上的正确作答概率Pi(θ)为:

其中,被试能力参数θ~N(0,1),项目区分度ln(a)~N(0,1),难度参数b ~N(0,1),D=1.7。
3.2 DIF项目模拟设计
本研究固定测验长度为50个项目,均为二级记分项目。50个项目的原始参数情况(见表2)。无DIF的项目在目标组与参照组中各参数不变,即不同组中能力相同的被试,其在该类项目上的正确作答概率相同;有一致性DIF的项目在两组中具有不同的难度,相同的区分度,因此通过改变其中一组被试的项目难度参数来设定有一致性DIF的项目;有非一致性DIF的项目在两组中具有不同的区分度,相同的难度,因此通过改变其中一组被试的项目区分度参数来设定有非一致性DIF的项目。
3.3 研究设计

表2 项目参数情况
两被试组的匹配变量为被试在无DIF的题目上的得分和。
本研究的自变量如下:样本量(300,800,1200,1600,2000),DIF值大小(0.25,0.5,1),DIF项目的比例(8%,16%,24%),DIF方法(MH和LR)。已有研究表明,要想得到合适的检出率,参照组和目标组的样本量至少分别要200~250人(Swaminathan&Rogers,1990;Rogers&Swaminathan,1993)。为了获得更加稳定的结果,本文选取了300作为最小样本量,并以2000作为最大样本量(见表2)。在8%的项目(4个项目)有DIF时,设定3题,6题,26题,30题有DIF,前两个项目为含一致性DIF的项目,后两个为含非一致性DIF的项目;在16%的项目(8个项目)有DIF时,设定3题,6题,9题,12题,26题,30题,34题,40题有DIF,前4个项目为含一致性DIF的项目,后4个题目为含非一致性DIF的项目;24%的项目(12个项目)有DIF时,设定3题,6题,9题,12题,17题,21题,26题,30题,34题,40题,43题,48题有DIF,同样前6个题目为含一致性DIF的项目,后6个题目为含非一致性DIF的项目。因此本研究的实验设计为5×3×3×2的混合设计,共计90种实验条件,每种条件下重复100次,共计9 000次。模拟运算用R-2.15.2进行。
因变量:I型错误率和检出率。统计学中I型错误为弃真错误,即当原假设为真(统计学意义上不显著)时,却错误地否定了原假设。在DIF分析中则表示,当原假设(题目没有DIF)为真时,却错误地否定原假设,认为题目含有DIF。如果一个DIF检测方法I型错误率高,那么就说明该方法不够好,会错误识别不含DIF的题目,而被错误识别出有DIF的题目可能会面临被修改或删除,从而也就增加了相应的工作量,浪费人力。检出率为统计学中的正确拒斥率,也被成为统计检验力,即原假设(题目没有DIF)为假时,正确地拒绝了原假设,认为题目有DIF。因此,检出率高就代表该方法好,能够很好地检测出有DIF的项目。
4 结果
4.1 I型错误率分析
表3呈现了MH和LR两种方法在不同条件下的平均I型错误率。

表3 MH和LR的平均I型错误率情况(α=0.05时)
由表3可以看出,MH和LR两种方法的I型错误率均在0.05左右,说明两种方法都比较好。MH的I型错误率随样本量有较小幅度的增加(0.052增至0.0550);且随着有DIF的项目比例的增加也有较小幅度的增加(0.0510增至0.0546);而LR的I型错误率在所有情况下都较稳定,保持在0.049~0.051。因此,可以看出MH方法的I型错误率变动范围比LR略大(MH:0.0510~0.0550;LR:0.0497~0.0517)。
另外也可以看到,MH的I型错误率总是略高于LR的I型错误率,在样本量=2000及DIF项目的比例=24%时,两种方法的I型错误率差异最大。在样本量=800时,两种方法的I型错误率都最小。
表4呈现了MH和LR两种方法的检出率情况。

表4 MH和LR的检出率情况
从表4可以看到,对于DIF类型来说,MH对非一致性DIF的检测相当差,对一致性DIF的检出率大大高于对非一致性DIF的检出率。对于一致性DIF,MH和LR在样本量小(NR=NF=300)时,检出率能达到0.5,且MH的检出率在所有样本量下都是略高于LR的(Swaminathan&Rogers,1990);对于非一致性DIF,LR的检出率则远远高于MH的,LR对两种类型的DIF检测都很好,适用于检测两种DIF类型。MH对非一致性DIF的检测很差,是因为MH是设计来用于检测一致性DIF的,其对非一致性DIF的检测不够敏感(Swaminathan&Rogers,1990;Li,Brooks,&Johanson,2012)。因此,两种方法的比较在接下来仅限于比较检测一致性DIF时的表现。
两种方法的检出率,不管是一致性DIF还是非一致性DIF,都随着样本量及DIF值的增加而增加,在样本量从300到800及DIF值从0.25增到0.5时,两种方法检出率的增长幅度最大。可以看到,在样本量大(NR=NF=2000)及DIF值大(DIF=1)时,除去MH检测非一致性DIF时,此时两种方法的检出率都很高,在0.9左右。
DIF项目的比例对两种方法的检出率的影响则不同。对一致性DIF来说,两种方法的检出率随DIF项目比例的增加而增加,在DIF项目比列达到24%(12个题目有DIF)时,两种方法的检出率都在0.8以上;而对非一致性DIF来说,检出率有所下降[MH:0.314(8%),0.230(24%);LR:0.803(8%),0.732(24%)]。
从表4还可以看出,在检测一致性DIF时,MH方法的检出率在样本量为1200时就已在0.8以上,而LR在1600才达到MH的水平。这可能是因为LR是参数方法,对样本量的要求较大,因此在样本量偏大时才能达到一个比较好的检出率。
5 讨论
本研究的结果与前人的研究结果一致,MH适合于检测一致性DIF,检测一致性DIF时,检出率高,且略高于LR。而LR在检测一致性和非一致性DIF时检出率都很好,但是其对样本量的要求较高。DIF项目的比例增加对检出率影响随着DIF类型的不同有所不同。总的来说,MH是检测一致性DIF非常好的方法,并且它不需要大样本,方法简单易用。因此ETS一直采用它对项目DIF作常规分析(余仁胜,1999)。当要研究其他方法时,通常以这个方法作为标准,将其他方法与之对比(曾秀芹,孟庆茂,1999)。LR是一个可以同时检测一致性DIF和非一致性DIF的很强大的方法,在样本量达到1500左右时,能够很好地发挥其优势。
项目功能差异是在我国的研究还有待进一步地深入,未来还有许多可以研究的方向,当两被试组能力水平不同时不同方法的DIF检测情况,不同匹配变量对DIF检测的影响,小样本时如何优化DIF检测等都值得进一步的研究。
[1]曹亦薇.项目功能差异在跨文化人格问卷分析中的应用[J].心理学报,2003,35(1):120-126.
[2]董圣鸿,马世晔.三种常用DIF检测方法的比较研究[J].心理学探新.2001,(1):43-48.
[3]刘文,边玉芳,陈玲丽,等.马洛-克罗恩社会赞许性量表在跨文化研究中的项目功能差异检验[J].心理科学,2010,33(6):1473-1476.
[4]鹿士义.汉语水平考试HSK的DIF研究[D].南京师范大学教育科学学院,2004:30.
[5]骆方,张厚粲.检验功能差异的两类方法——CFA和IRT的比较[J].心理学探新,2006,1(26):74-78.
[6]任杰.中国境内外HSK成绩公平性的分析[J].语言教学与研究,2002,5:69-74.
[7]严芳,张增修.用Logistic Regression侦察题目差异功能[J].应用心理学,2001,7(1):57-62.
[8]余仁胜.访美观感[J].考试研究动态,1999(3).
[9]于媛颖.多种DIF检测方法的比较研究[D].北京语言大学,2004.
[10]曾秀芹,孟庆茂.项目功能差异的简介[J].心理学探新,1998(1).
[11]曾秀芹,孟庆茂.项目功能差异及其检测方法[J].心理学动态,1999(2):41-47.
[12]张颖,赵世明.医师资格考试中的项目功能差异研究[J].中国考试,2004(10):23-26.
[13]Li,Y.,Brooks,G.P.,&Johanson,G.A.Item Discrimination and Type IError in the Detection of Differential Item Functioning.Educational and Psychological Measurement,2012,72(5),847-861.
[14]Narayanan,P.,&Swaminathan,H..Identification of items that show nonuniform DIF[J].Applied Psychological Measurement,1996(20):257-274.
[15]Rogers,H.J.,&Swaminathan,H..A comparison of logistic regression and Mantel-Haenszel procedures for detecting differential item functioning[J].Applied Psychological Measurement,1993(17):105-116.
[16]Swaminathan,H.&Rogers,H.J.Detectingitem functioningusinglogistic regression procedures[J].Journal of Educational Measurement,1990(27):361-370.

