最小差异采样的主动学习图像分类方法

吴健，盛胜利，赵朋朋，崔志明

（1. 苏州大学 智能信息处理及应用研究所，江苏 苏州 215006；2. 美国阿肯色中央大学 计算机科学系，阿肯色州 康威 72035-0001）

1 引言

图像分类是计算机视觉和模式识别领域中的一个重要问题，其主要内容是采用分类算法建立分类器模型，然后利用模型进行待分类图像的分类[1,2]。目前图像分类技术正在国民经济中发挥着越来越大的作用。比如，借助图像分类技术可以高效地从大量细胞图片中准确识别出病变细胞，并确定其对应癌症类别，提高医务人员的工作效率与治疗水平[3]；遥感图像信息含量大、物体种类多，遥感图像分类也一直是遥感图像研究的核心问题[4]。不同的分类器模型性能不尽相同，训练分类器是分类研究的关键部分。分类器训练是在训练样本集上进行优化的过程，是一个机器学习过程。在传统的监督学习中，分类器通过对大量有标注的训练样本进行学习，从而建立模型用于预测未见样本的类别。随着数据收集和存储技术的飞速发展，收集大量未标注的样本已变得相当容易，而获取大量有标注的样本则相对较为困难，因为获得这些标注可能需要耗费大量的人力物力。因此，在有标注样本较少时，如何利用大量的未标注样本来改善学习性能成为当前机器学习研究中最受关注的问题之一。

主动学习是一种新的利用未标注样本的学习技术，主动学习的核心思想是通过启发式学习策略，从样本数据集中挑选少部分的高信息含量的样本子集训练得到性能优良的分类器模型[5]。在学习过程中，学习引擎将优选的未标注样本交由人工专家进行标注。主动学习在很多现代的机器学习问题中有很广泛的应用需求，比如，大量未标注样本易于获得，但是标注困难，耗时、代价较大。Lewis等人[6]提出了基于池的主动学习采样策略，算法维护一个固定分布的由大量未标注样本组成的样本池，采样策略计算所有未标注样本的信息含量进行比较，选择信息含量高的未标注样本交由人工专家标注。Lewis等人指出，不确定性采样能够大幅度地减小训练数据的规模，可以有效地应用于小样本的训练环境。基于池的采样策略成为当前研究最为深入、应用最为广泛的采样策略，在文本分类[7,8]、图像分类[9,10]、图像检索[11]、视频检索[12]等领域都有较好的应用。

主动学习中的样本采样策略主要可以分成 2类：不确定性采样(uncertainty sampling)和委员会投票选择(QBC, query-by-committee)[13]。

基于不确定性的采样策略是适用性最广的一类采样策略，最基本的做法是使用分类器直接估计未标注样本属于各类别的后验概率值，选择后验概率最接近于0.5的样本。例如，Lewis等人[14]采用了不确定性采样的主要思想将其应用于决策树模型，采用一个分类器模型计算所有未标注样本的不确定性，选择分类器最不确定的样本作为返回的待标注样本。样本采样策略的第2类方法是QBC算法。QBC的方法首先由Seung等人[15]提出，该方法通过构建委员会，选择委员会成员模型投票不一致性最高的样本作为待标注样本交由人工专家标注。自从 Seung等人构建第1个由2个随机假设模型组成的委员会后，QBC算法在各种分类模型的实际应用中收到了较好的效果[16]。

委员会投票选择是一种基于版本空间缩减的主动学习采样策略，其核心是构建高效的具有较强泛化能力的委员会。针对委员会成员模型投票不一致性的度量问题，提出了一种基于最小差异采样的主动学习图像分类方法。利用委员会成员模型投票概率较高的 2个类别的概率值的差异来度量委员会的投票不一致性，选择概率差异最小的样本交由人工专家标注。在本文实验部分，将提出的新方法与EQB算法及nEQB算法在多个数据集上进行实验对比，并对组成决策委员会的成员模型的数目设置问题进行分析和讨论，结果表明本文方法在标注样本数量相同的情况下能够有效提高分类准确率。

2 委员会投票

针对未标注样本集，与之一致的所有统计学习模型被称为它的解释空间。解释空间越大，则能够选择的模型就越多。当解释空间只有一个点时，统计学习模型就被唯一确定。因此，一种基于理论驱动的查询选择框架总是优先选择那些能够显著缩减其解释空间的样本进行人工标注。QBC算法基于这种思想被提出，它是一种通过版本空间缩减实现主动样本采样的被广泛使用的著名算法。通过给定不同的假设条件，QBC构建出不同的委员会成员模型来度量未标注样本集中每一个样本的信息含量。最具信息含量的样本是委员会成员模型投票最不一致的那些样本，这种策略可以高效地提升分类器模型的分类性能，本质上与不确定性采样策略相似。

版本空间缩减采样策略的主导思想是选择能最大程度缩减版本空间的样本进行标注，Seung等人基于该思想构建了第1个由2个随机假设模型构成的委员会。QBC算法的工作原理如图1所示。

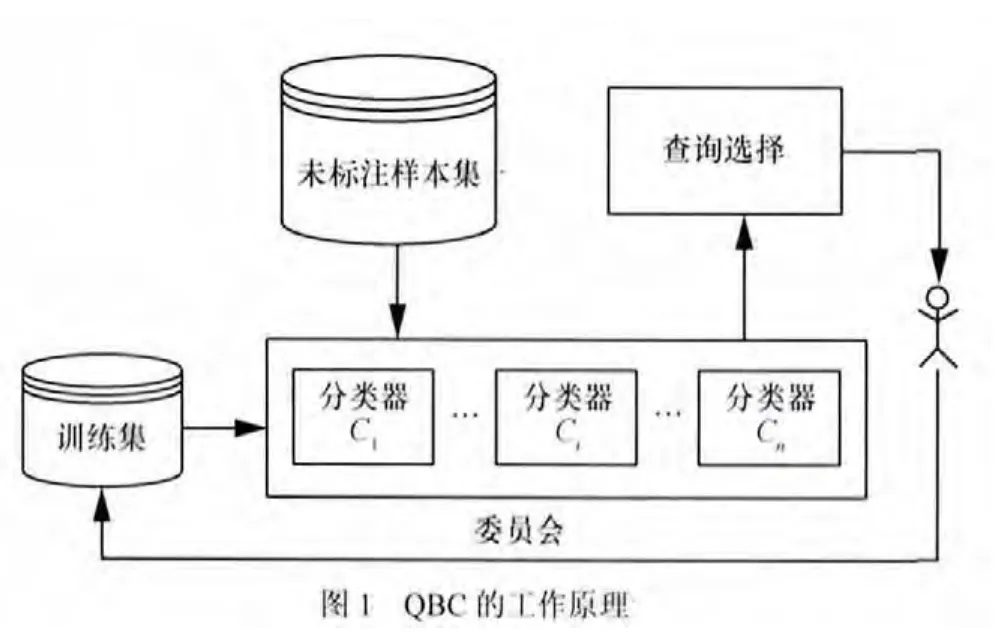
QBC算法的具体步骤是：首先，基于初始训练样本集根据给定的假设条件，构建出由n个成员模型组成的委员会；然后由组成委员会的各个成员模型对未标注样本集中的每一个样本进行投票，选出委员会成员模型投票最不一致的样本交由人工专家进行标注；最后将所选样本更新到标注样本集进行分类器更新。如此重复直至满足停止条件。

这种采样策略的目的是构建一个高效的具有很强泛化能力的委员会，通过对基于 QBC思想提出的各种现有方法进行归类分析，该采样策略主要包括2个研究内容：一是如何构建一个高效的委员会，比如Abe等人[17]采用boosting和bagging 2种集成学习方法构建委员会，分别提出了 boosting-QBC和bagging-QBC的委员会构建策略。另一个是如何度量委员会成员模型对于未标注样本集的投票不一致性，比如Tuia等人提出的EQB[18](entropy query-by-bagging)方法以及在此基础上改进得到的nEQB[19](normalized entropy query-by- bagging)方法。本文拟对样本投票不一致性的度量进行深入研究，下面对EQB和nEQB进行简要介绍。

Tuia等人提出了原始的EQB算法，采用bagging构建委员会。首先基于自展法定义n个训练集，然后使用训练集训练SVM分类器预测候选样本的标签，最后得到针对每一个候选样本的n个可能标签。在文献[18]中，基于n个分类器预测结果计算投票熵的采样策略被应用到多分类问题中。一种新的用于度量委员会成员模型投票不一致性的采样策略被提出，如式(1)所示。

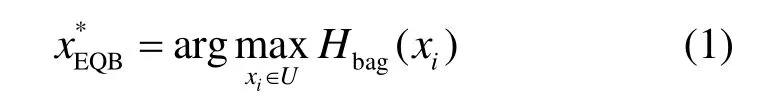
其中， Hbag(xi)是熵的实证测度，定义为

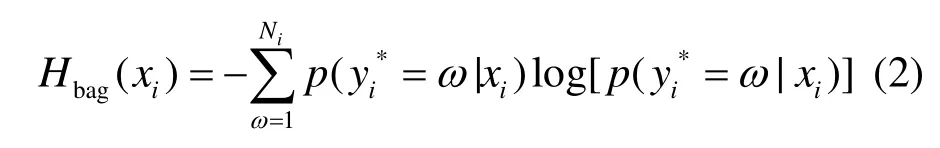
然而，EQB中投票熵的值存在着被未标注样本xi所属预测类别的个数Ni所影响的问题。考虑到这一现实，Copa等人提出了无偏置的样本不确定性度量函数，以考虑采样样本的多样性。EQB方法的一种改进算法 nEQB算法被提出，这种方法对 EQB方法进行归一化处理，基于归一化最大熵的启发式采样策略描述如下

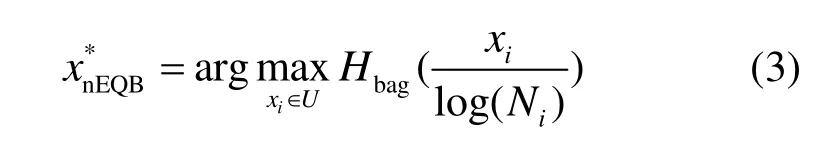
nEQB算法保持了EQB算法的优点，同时强化了被采样样本的多样性。所有决策边界上的样本的不确定性较高，这些样本被优先考虑。

3 本文方法

3.1 问题分析

QBC算法的研究重点是如何有效地构建委员会，以及如何度量成员模型对未标注样本的投票不一致程度。根据文献[19]的分析，EQB算法中投票熵的计算会随着未标注样本所属类别个数的变化而变化，当所属类别数目增加时，未标注样本投票熵值的上限也将增加。比如，某样本被预测为2个类别时的最大熵值要比被预测为多个类别时的最大熵值小，这种情况则会优选那些被预测为多个类别的样本，导致样本的不平衡采样。nEQB算法针对该问题进行了归一化处理，在计算样本投票熵值的同时考虑样本所属类别数目的变化，将求得的 EQB值除以 Ni值以消除样本所属类别数对投票熵值的消极影响，使样本采样保持无偏置。

根据以上分析，可以看到 nEQB算法对 EQB算法存在的偏置采样问题进行了校正，但该问题并没有得到有效的解决，以下对该问题进行深入分析。在此假定已构建一个具有100个成员模型的委员会，未标注样本集样本的类别总共为10类，图2是对熵度量方法缺陷的分析，图2(a)为样本a采用EQB算法和nEQB算法计算得到的熵值，从图中可以看出样本 a所属类别数目为 7。图 2(b)为样本 b采用EQB算法和nEQB算法计算得到的熵值，从图中可以看出样本b所属类别数目为8。通过对比可以发现 EQB确实存在偏置采样的问题，即样本所属类别数目较高时样本熵值偏大，由于样本b的熵值较高，则认为其信息含量较高。

根据EQB算法的采样策略，样本b由于熵值较高，将会被优先选中。而综观委员会的100个成员模型针对样本a和样本b预测类别的概率分布，样本a从属于第2类和第6类的概率非常接近，而样本b从属于第6类的概率明显较大，可以看出，样本a比样本b具有更大的不确定性，从最大程度优化分类器性能的角度而言，样本a能够更大程度地提升分类器的泛化性能。但是，EQB算法的投票结果与此相反，会优选样本b。

nEQB算法在EQB算法的基础上考虑了无偏置样本采样问题，除以样本所属类别数目的对数，降低样本所属类别数目对投票熵值的不利影响。经过归一化处理后，样本a和样本b的熵值分别被校正为0.284 5和0.315 7，但校正后的结果并不理想，可以看出样本b的熵值依然高于样本a的熵值，根据信息熵的定义，样本b的信息含量高于样本a，采样结果仍是样本b。

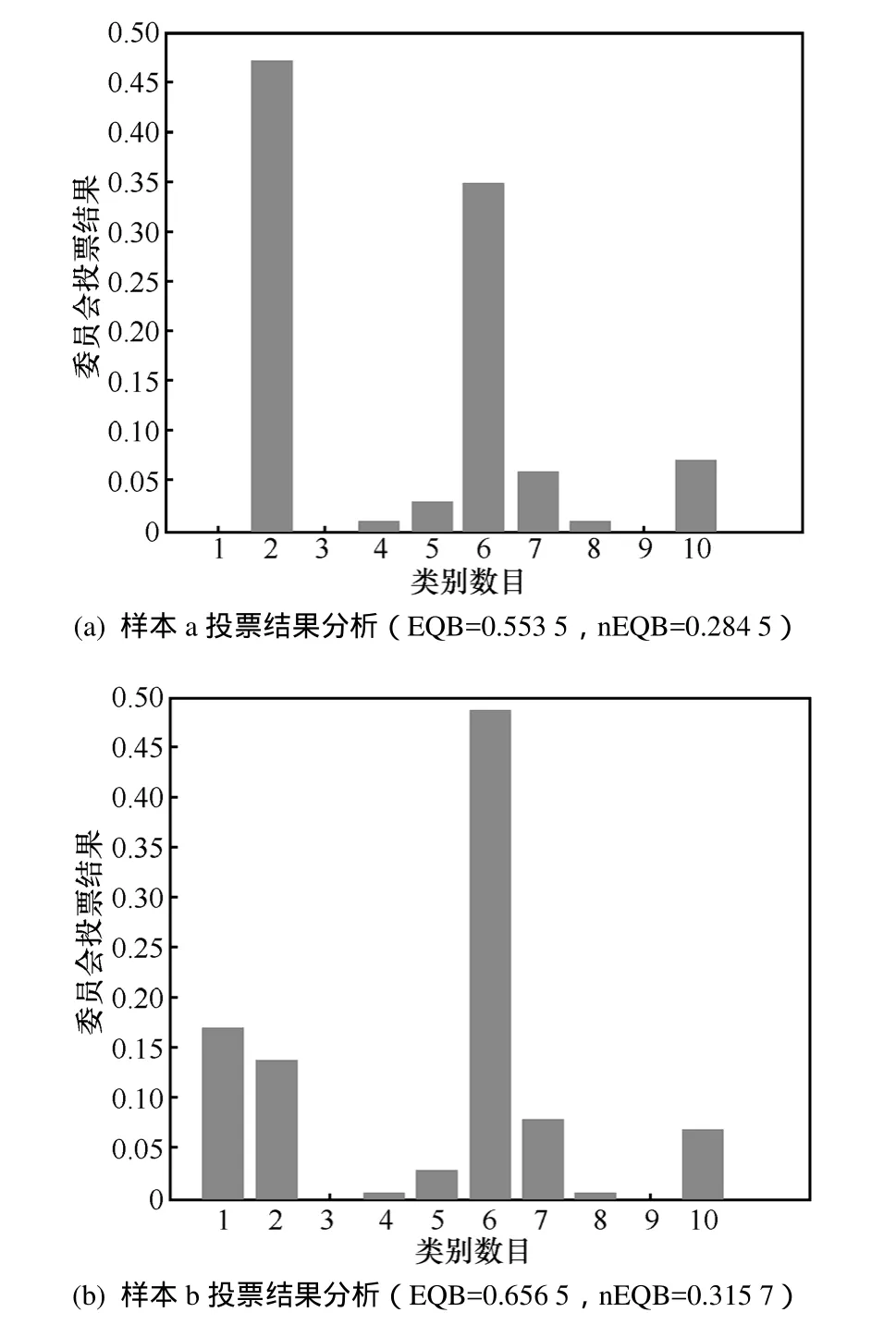
图2 熵度量的缺陷分析

综上所述，虽然基于熵的方法度量委员会成员模型对样本的投票不确定性常常好于随机采样，且易于扩展应用到多分类问题中，但它存在着一定的缺陷。采用熵方法的问题之一是它的值会受到不重要类别的严重影响，如图2所示，委员会对样本a的预测类别主要集中在第2类和第6类，对样本b的预测类别主要集中在第6类，而在计算熵的时候则考虑了所有的预测类别，这导致了概率较小的预测类别对投票熵计算的影响。而从分类角度来讲，分类器对图2(a)的情形更为不确定，因为它分配了2个相近的概率值给2个预测类别。对于图2(b)，分类器对于样本b的分类结果具有较高的自信，但那些不重要的预测类别导致了较高的熵值，这个问题在分类任务的类别更高时会更加突出。因此，笔者更为关心的是投票概率相近类别对样本不确定性度量准则的影响。

3.2 最小差异采样

与基于投票熵度量委员会成员模型投票不一致性不同的是，本文基于投票概率较低的类别是样本真正类别的可能性较低的假设，拟采用一种更为贪婪的方法来考虑委员会投票不一致性度量问题。本文将委员会投票概率较高的2个类别概率值的差异作为成员模型投票不一致性的度量，以此为依据选择高信息含量样本。本文首先给出投票概率差异的定义。

定义1 投票概率差异

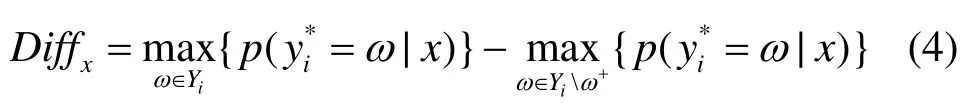
由于这是2个预测类别投票概率差异的比较，差异越小的样本其投票不一致性越高，亦即样本不确定性越高，笔者称之为最小差异采样（MDS,minimal difference sampling）。从分类角度来看，该度量方法是委员会成员模型投票不一致性估计的一种更为直接的方法，以图2中的样本a和样本b为例，样本a从属于类别2和类别6的投票概率差异较大，样本b从属于类别1和类别6的投票概率差异较大，从最小差异的定义来说，样本a将会被优先选择。

本文采用一种基于最小差异采样的准则，其只考虑样本分类可能性最大的2个类别，忽略其他对该样本的分类结果影响较小的类别。从另外一个角度解释，该准则可看作是对样本分类不确定性估计的一种贪婪近似。通过最小化最高类别和次高类别的概率差值，即最大化样本的分类不确定性，可得MDS度量准则如式(5)所示。

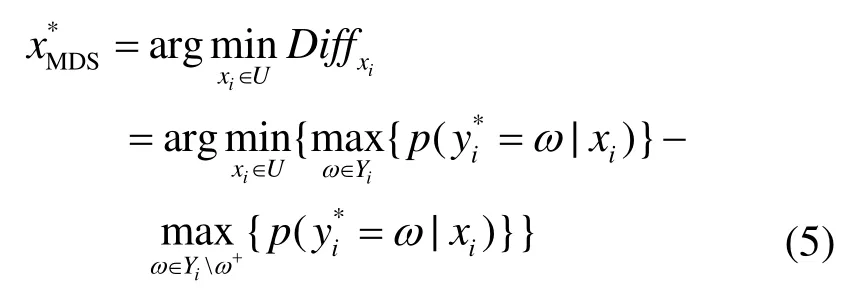
投票熵是一种样本分类不确定性的估计，而MDS度量是一种贪婪估计。从改变分类器分类边界的角度来看，MDS度量可以被认为是一种选择高信息含量样本的高效估计方法。基于MDS度量准则，衡量所有未标注样本相对于当前分类器的不确定性，从中选出最不确定的样本集合。

3.3 算法描述

由以上分析可知，MDS方法利用委员会投票概率较高的2个类别的概率值的差异来度量成员模型的投票不一致性，从而有效地选择最不确定的样本。通过从未标注样本集中选出最具信息含量的样本，交由人工专家标注，并更新至标注样本集，从而更新分类器模型，如此迭代，直至完成分类器的学习。

本文方法的完整描述如图3所示。

图3 MDS主动学习图像分类方法

在图3算法中，首先需要基于标注样本集L进行bagging（bootstrap aggregation）采样[20]定义n个训练集，bagging算法过程是从样例分布中进行多次独立同分布采样，使用所选样本训练候选假设，其能够减少假设偏置的影响。然后，基于 bagging重采样技术得到的结果构建一个具有n个成员模型的决策委员会 {C1, C2,… ,Cn}，针对每个未标注样本，可用式(4)计算得到其投票不一致性度量的结果。

本文方法通过委员会投票的方式进行样本采样，其与不确定采样的区别在于：不确定性采样是直接通过当前分类器模型直接估计未标注样本的后验概率分布，然后根据一定的启发式策略优选不确定性最高的样本进行标注；而委员会投票算法是通过委员会成员模型对未标注样本进行投票，根据成员模型投票的结果选择投票最不一致的样本交由人工专家进行标注，实质上是通过委员会成员模型的投票不一致性间接地反映样本的不确定性。因此，本质上委员会投票算法仍是继承了不确定性采样的思想。

4 实验结果与分析

本文在3个图像分类数据集上验证本文提出的MDS主动学习图像分类方法的有效性，其中，一个是人工数据集，另外2个来自UCI数据集[21]，UCI数据集是常用测试数据集。在文献[18]中，EQB的实验效果整体优于 MS（margin sampling）、MS-cSV。MS和MS-cSV的区别之处为成批选择候选样本时，后者会考虑样本之间的多样性。在文献[19]中，nEQB算法整体效果要优于 BT（breaking ties）和EQB。因此，实验中将提出的方法与 EQB算法和nEQB算法在同等条件下进行比较，具体体现在相同数量标注样本下的分类准确率、成员模型数目对分类准确率的影响等方面。实验中使用Torch库[22]实现多类SVM分类器，采用一对多的方式来处理多类分类问题，用于输出各个未标注样本从属于每个可能类别的概率。

4.1 人工数据集

为验证本文方法的有效性，首先在人工数据集上进行实验。此人工数据集共36类，类别为A~Z和0~9，使用36种不同字体构造训练图像样本集，28种不同字体构造测试图像样本集，则训练图像集数目为1 296，测试图像集数目为1 008。使用图像像素值的统计信息，根据一固定子区域内像素百分比信息提取每张图像的二值特征，每张图像对应一个35维的特征向量。

设置初始样本个数为 50个，委员会成员数目为10，每次迭代加入到标注样本集的样本数为5，图4显示了通过3种方法采样训练分类器模型得到的分类结果。通过对分类准确率变化曲线进行观察，在迭代初期，采用各种样本选择方法的分类性能相差不大，这是由于在迭代初期，训练样本的数量较少，训练得到的分类器不是很准确，在这种情况下，各种样本选择方法都近似于随机选择。EQB算法在训练样本数为 95时，由于所选样本的信息含量较低，EQB算法的分类准确率出现了一段较大幅度的下降，而nEQB算法保持了分类准确率的稳定。之后3种方法随着标注样本的不断加入，分类准确率逐步提高。

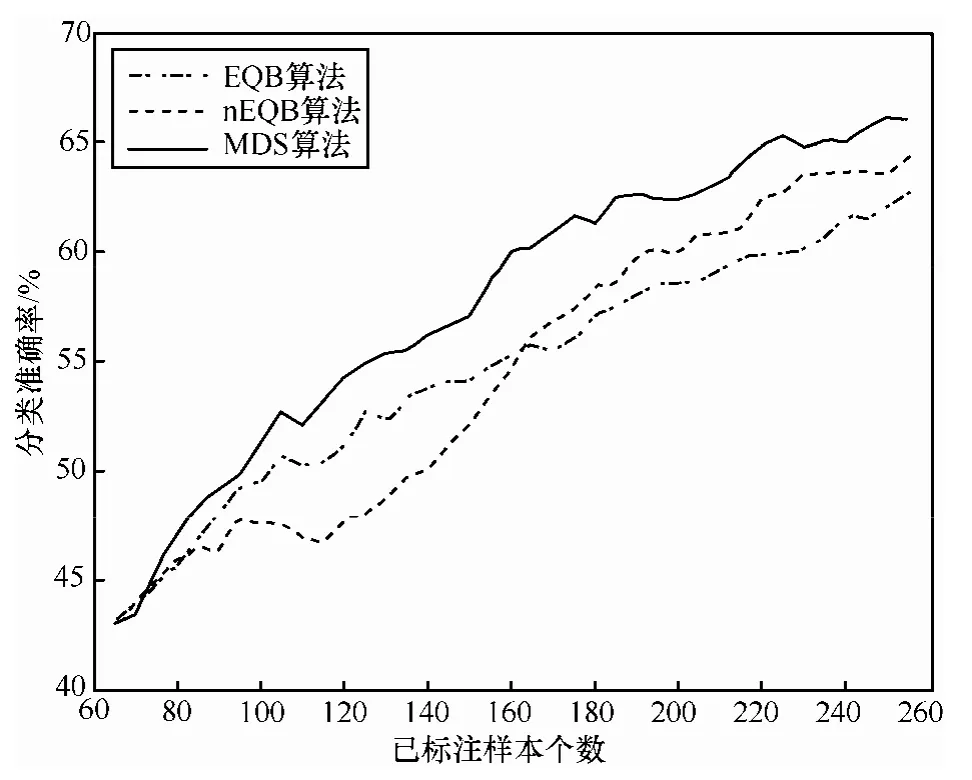
图4 人工数据集上分类准确率

从实验结果来看，由于nEQB算法在计算样本的投票熵时考虑了EQB算法存在的采样偏置问题，对样本的投票熵进行归一化处理，在分类准确率上的表现也说明了这一点，实验结果相比 EQB算法占优。经过刚开始的交汇期之后，当标注样本数达到80之后，MDS方法开始显现优势，逐渐与EQB和nEQB算法拉开差距，当标注样本达到240时，分类准确率达到80%以上，此时EQB和nEQB算法的分类准确率分别在70%和75%左右。本文MDS算法基于委员会投票最小差异采样，考虑样本分类可能性最大的2个类别，采用贪婪估计法优选高信息含量的样本进行标注，实验结果表明这种启发式准则能够很好地度量未标注样本的投票不一致性，选择的样本更有利于改善分类器的分类性能和提升分类器模型的泛化能力。

4.2 UCI数据集

在4.1节实验中使用的是人工数据集，本节将3种算法在标准数据集上进行实验以验证算法的有效性。UCI数据集是常用的标准测试数据集，选择了 UCI数据集中的美国邮政手写体数字图像集（USPS）和英文字母数据集（letters）2个数据集，类别分别为10类和26类。

1) 手写体数字图像集（USPS）

该数据集中样本类别分布为 0~9，每个样本有256维特征，训练集大小为5 000，测试集大小为4 298。设置初始样本个数为36，委员会成员数目为10，每次迭代加入到标注样本集的样本数为5，图5显示了通过3种方法采样训练分类器模型得到的分类结果。

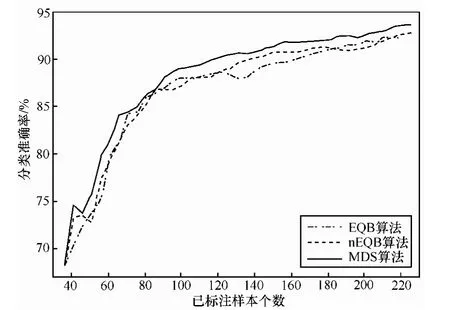
图5 USPS数据集分类准确率

图5显示了3种方法在USPS图像集上分类准确率随标注样本数增加的变化曲线，该数据集总共类别数为 10，类别数相对偏少，3种方法训练的分类器模型都能取得较好的分类精度。当分类器迭代更新结束时，3种算法都能收敛于比较高的分类精度。将EQB和nEQB 2种方法进行比较，nEQB算法起初略占优势，但随着迭代的进行，2种算法开始交织在一起，分类精度大体相当。与此同时，本文方法在此数据集上一直优于EQB和nEQB算法：迭代初期，3种方法效果差不多，随着标注样本数的增加，本文方法的作用逐渐体现出来，明显优于其他2种方法。当标注样本数目相同时，本文方法的分类准确率较高，说明在相同人工标注负担的前提下，本文方法更能提高分类精度。从纵轴方向来看，在获得相同准确率的前提下，本文方法要求的标注样本数较其他2种方法更少，减轻了人工标注的负担。

2) 英文字母数据集（letters）

该数据集样本类别分布为 A~Z，每个样本有 16维特征，训练集大小为10 000，测试集大小为10 000。设置初始样本个数为 65，委员会成员数目为 10，每次迭代加入到标准样本集的样本数为5，图6显示了通过3种方法采样训练分类器模型得到的分类结果。通过分析letters图像数据集实验结果可以看出，在曲线的前半段，nEQB算法的表现明显弱于EQB算法，但在曲线的后半段，nEQB算法分类精度的提升速度开始高于 EQB算法，迭代结束时分类精度高于EQB算法近2个百分点。

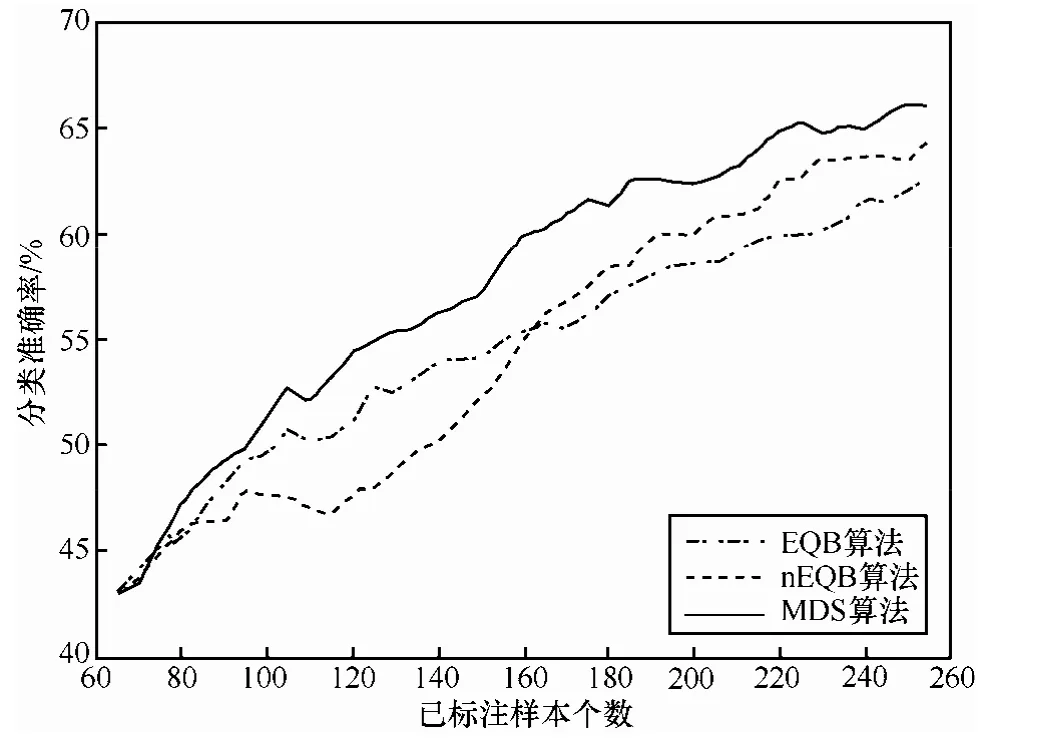
图6 letters数据集分类准确率

Letters数据集类别共有26类，类别相对较多，所以3种方法在迭代结束时分类准确率整体不高。但从图6中可以看出，本文方法的分类精度从开始到结束都能有较好的表现，一直优于EQB和nEQB算法，体现出一定的算法优势。虽然只考虑很少一部分未标注样本，但本文方法所基于的最小差异采样启发式准则依然能够选出最具信息含量的样本，相对于其他2种方法，显著提高了分类准确率。本文方法基于MDS度量准则，衡量所有未标注样本相对于当前分类器的不确定性，从中选出最不确定的样本集合，是一种选择高信息含量样本的高效估计方法。

4.3 委员会成员数目讨论

以上通过3个图像分类数据集验证了本文提出的MDS主动学习图像分类方法的有效性。构建委员会时成员模型数目的设定是一个值得讨论的问题，本节对成员模型的数目设定进行讨论。上述 3个数据集的实验结果一方面验证了本文方法的有效性，另一方面也说明了EQB和nEQB算法的效果差异。nEQB算法针对EQB的采样偏置问题进行了纠正，对未标注样本的投票熵进行了归一化处理，从上述实验可以看出，nEQB算法要优于EQB算法，这说明其对EQB的改进是有效的。由于nEQB算法要优于 EQB算法，在本节讨论中，仅讨论本文方法和nEQB方法在成员模型设置不同时其分类准确率随标注样本增长的变化曲线，成员模型数目分别设置为5、10、15和20，通过比较在不同参数设置下2种算法的性能表现分析讨论成员模型数目的设置问题。图7(a)和图7(b)分别显示了nEQB算法和本文方法在不同成员模型数目设置情形下的分类准确率随标注样本变化的情况。

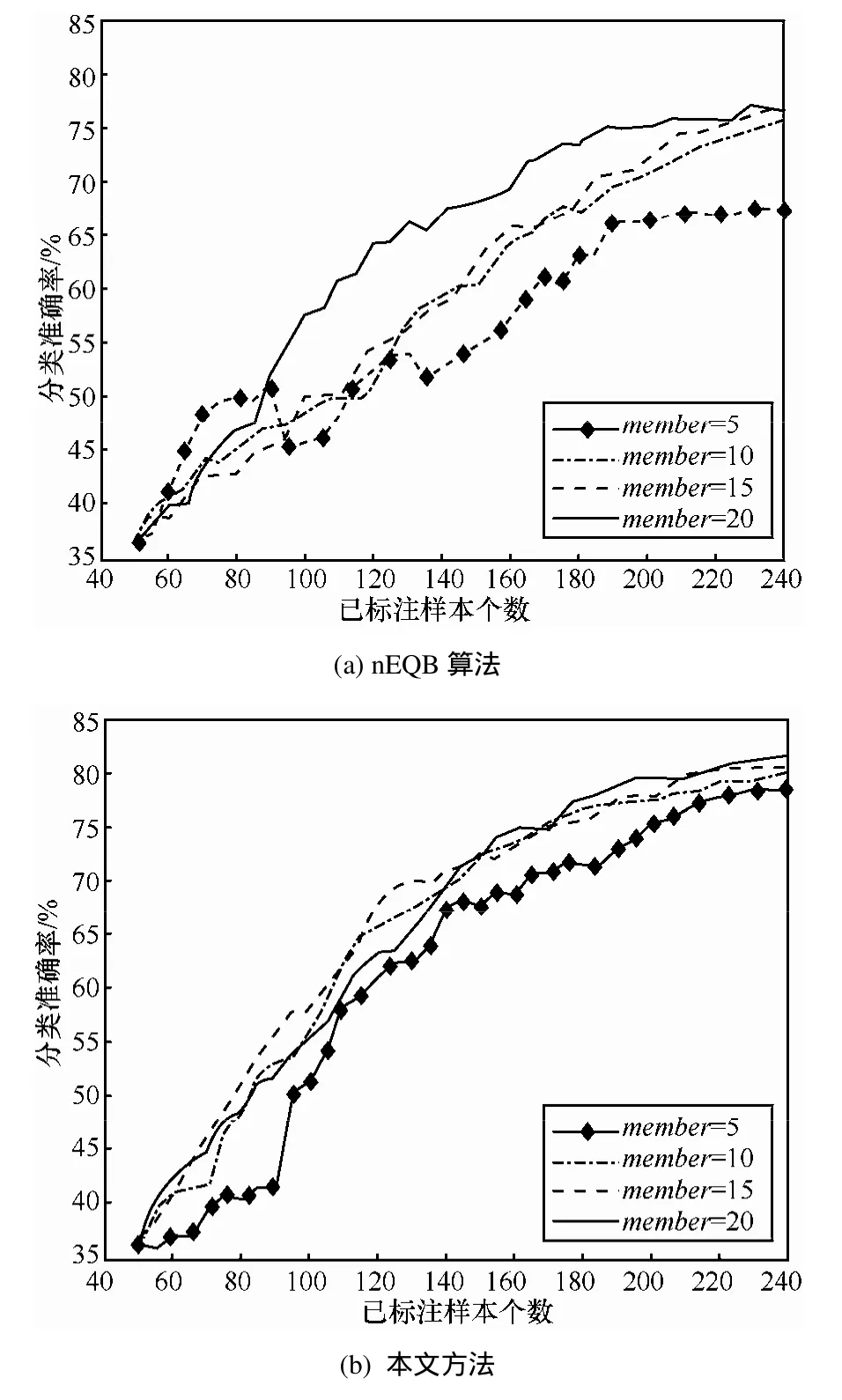
图7 委员会成员模型数目实验分析

图7(a)显示了nEQB算法在成员模型数目为5、10、15和20时的分类精度变化情况，随着成员模型数目的增加，在相同标注样本数量的前提下，其对应的分类精度都会有所提升。当成员模型数目为5时，迭代结束时的分类准确率为67.46%，当成员模型数目为10、15和20时，分类准确率有较大的提高，迭代结束时的分类准确率均在75%左右。图7(b)显示了本文方法在成员模型数目为 5、10、15和 20时的分类精度变化情况，随着成员模型数目的增加，在相同标注样本数量的前提下，其对应的分类精度亦有所提升。当成员模型数目为5时，迭代结束时的分类准确率为78.67%，当成员模型数目为10、15和20时，分类准确率有一定的提高，迭代结束时的分类准确率均在80%以上。综合图7(a)和图 7(b)来看，nEQB算法受成员模型数目的影响较大，而本文方法在成员模型数目为 10时就能较好地收敛，且收敛于比较高的分类精度。成员模型的数目越大，分类准确度相对会越好，但需权衡成员模型数目的设置所带来的时间开销。

5 结束语

本文针对委员会投票不一致性度量问题提出了一种基于最小差异采样的主动学习图像分类方法，方法首先基于标注样本集进行bagging采样，

然后基于 bagging采样的结果构建决策委员会对未标注样本集中每个样本的不确定性进行度量。实验结果表明本文方法能有效提高分类精度。委员会投票选择算法通过成员模型投票的不一致性间接反映样本的不确定性，充分利用已标注样本集来对未标注样本进行估计。后续研究将进一步考虑未标注样本集的分布信息，保证选择的样本可以有效地降低预期误差，提高分类器模型的泛化能力。

[1] 钟桦, 杨晓鸣, 焦李成. 基于多分辨共生矩阵的纹理图像分类[J].计算机研究与发展, 2011, 48(11):1991-1999.ZHONG H, YANG X M, JIAO L C. Texture classification based on multiresolution co-occurrence matrix[J]. Journal of Computer Research and Development, 2011, 48(11):1991-1999.

[2] CIRESAN D, MEIER U, SCHMIDHUBER J. Multi-column deep neural networks for image classification[A]. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition[C]. Rhode Island, USA, 2012.3642-3649.

[3] XU Y, ZHU J Y, CHANG E, et al. Multiple clustered instance learning for histopathology cancer image classification, segmentation and clustering[A]. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2012)[C]. Rhode Island, USA, 2012.964-

[4] 9V7O1.LPI M, TUIA D, KANEVSKI M. Memory-based cluster sampling for remote sensing image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(8):3096-3106.

[5] SETTLES B. Active Learning Literature Survey[R]. Madison:University of Wisconsin, 2010.

[6] LEWIS D D, CATLETT J. Heterogenous uncertainty sampling for supervised learning[A]. Proceedings of International Conference on Machine Learning (ICML 1994)[C]. New Brunswick, NJ, USA,1994.148-156.

[7] OLSSON F. A Literature Survey of Active Machine Learning in the Context of Natural Language Processing[R]. Swedish Institute of Computer Science, 2009.

[8] FU Y, ZHU X, LI B. A survey on instance selection for active learning[J]. Knowledge and Information Systems, 2013, 35(2):

[9] 2JO49S-H28I 3A. J, PORIKLI F, PAPANIKOLOPOULOS N P. Scalable active learning for multi-class image classification[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11):2259-2273.

[10] LI X, GUO Y. Adaptive active learning for image classi fi cation[A].Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2013)[C]. Portland, Oregon, USA, 2013.859-866.

[11] HOI S C H, JIN R, LYU M R. Batch mode active learning with applications to text categorization and image retrieval[J]. IEEE Transactions on Knowledge and Data Engineering, 2009, 21(9):

[12] 1W2A33N-G12 4M8,. HUA X S. Active learning in multimedia annotation and retrieval: a survey[J]. ACM Transactions on Intelligent Systems and Technology, 2011, 2(2):1899412-1899414.

[13] 梁爽, 孙正兴. 面向草图检索的小样本增量有偏学习算法[J]. 软件学报, 2009, 20(5): 1301-1312.LIANG S, SUN Z X. Small sample incremental biased learning algorithm for sketch retrieval[J]. Journal of Software, 2009,

[14] 2L0E(W5):I1S3 0D1- 1D3,1 2G.ALE W A. A sequential algorithm for training text classifiers[A]. Proceedings of the 17th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval[C]. Dublin, Ireland, 1994.3-12.

[15] SEUNG H S, OPPER M, SOMPOLINSKY H. Query by committee[A]. Proceedings of the Fifth Annual Workshop on Computational Learning Theory[C]. Pittsburgh, PA, USA,

[16] 1吴99伟2.宁28,7 -刘29扬4., 郭茂祖等. 基于采样策略的主动学习算法研究进展[J]. 计算机研究与发展, 2012, 49(6): 1162-1173.WU W N, LIU Y, GUO M Z, et al. Advances in active learning algorithms based on sampling strategy[J]. Journal of Computer Research and Development, 2012, 49(6): 1162-1173.

[17] ABE N, MAMITSUKA H. Query learning strategies using boosting and bagging[A]. Proceedings of the Fifteenth International Conference(ICML'98)[C]. Madison, Wisconsin, USA, 1998.1-9.

[18] TUIA D, RATLE F, PACIFICI F, et al. Active learning methods for remote sensing image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(7): 2218-2232.

[19] COPA L, TUIA D, VOLPI M, et al. Unbiased query-by-bagging active learning for VHR image classification[A]. Proceedings of SPIE Remote Sensing[C]. Toulouse, France, 2010.783001-783008.

[20] BREIMAN L. Bagging predictors[J]. Machine learning, 1996, 24(2):123-140.

[21] ASUNCION A, NEWMAN D J. UCI machine learning repository.[EB/OL]. http://www.ics.uci.edu/mlearn/ MLRepository.html, 2007.

[22] COLLOBERT R, BENGIO S, MARIETHOZ J. Torch: A Modular Machine Learning Software Library[R]. Technical Report, 2002.