自适应视野的人工鱼群算法求解最短路径问题
马宪民,刘妮
(西安科技大学 电气与控制工程学院,陕西 西安 710054)
1 引言
最短路径是智能车辆导航系统中的一个关键问题,在求解最短路径的算法中,目前国内外公认的较好算法有经典的迪杰斯特拉(Dijkstra)及弗洛伊德(Floyd)算法,但时间复杂度是此2种算法的瓶颈[1~3]。随着人工智能研究的深入,一些新的智能优化算法不断被提出,包括遗传算法、蚁群算法、粒子群算法、人工鱼群算法等。遗传算法的主要缺点是对于结构复杂的组合优化问题,搜索空间大,搜索时间比较长,往往会出现早熟收敛的情况;对初始种群很敏感,初始种群的选择常常直接影响解的质量和算法效率[4]。基本蚁群算法搜索时间长,而且容易出现停滞,存在着收敛速度慢、易陷入局部最优等缺陷;而模型中各参数的取值更直接关系到算法的收敛速度和全局搜索能力[4,5]。粒子群算法虽然收敛速度较快,但精度较低、易发散,容易陷入局部最优解[4]。而人工鱼群算法(AFSA,artificialfish swarm algorithm)顽健性强、对初值的敏感性小、简单(只需比较目标函数)、易实现,而且具有较强的跳出局部极值点的能力,即全局收敛性好,这就能为最短路径问题搜索到准确的全局最优解。
例如,文献[6]将改进的人工鱼群算法应用于交通路径诱导系统数据库优化查询中,算法提高了最优路径查询的效率。文献[7]基于有限适合启发式算法与人工鱼群算法相结合,完成了车辆最优调度路径的准确迭代计算,缩短了计算时间,克服了传统方法收敛速度慢的缺陷,高效地完成了最优路径的准确选择。
因此,本文选择人工鱼群算法求解静态道路网络上指定起点到终点的最短路径,并且针对基本人工鱼群算法在后期收敛速度慢和计算量大的缺陷,提出了基于视野自适应的改进算法。该改进算法只对人工鱼的觅食行为的视野进行改变,使其随着迭代次数的增加而逐渐减小,从而有效地加快了算法的收敛速度,减小了计算量。
2 基本人工鱼群算法
人工鱼群算法是我国学者李晓磊等人在 2002年模仿鱼类行为特点提出的一种基于动物自治体的优化策略[8]。该算法的基本思想是[9]:在一片水域中,鱼类聚集最多的地方一般就是这片水域中食物最为丰富的地方;根据鱼类的这个特点构造人工鱼,模仿鱼群的觅食、聚群、追尾等行为,每条人工鱼对应一个优化解,人工鱼生存的虚拟水域对应于优化问题的解空间,食物浓度对应于目标函数值,通过人工鱼群在虚拟水域中游动实现寻优。人工鱼群行为的算法描述如下。
1) 觅食行为:设人工鱼的当前状态为aX,在其视野范围内随机选择一个状态bX ,为

其中,函数 ()Rand 产生0到1之间的随机数,Visual为视野范围。如果食物浓度(求极小值问题)则向该方向前进一步,为
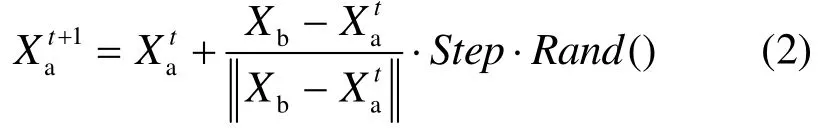
其中,Step为移动步长。反之,再重新随机选择状态bX,判断是否满足前进条件;试探一定次数后,如果仍不满足前进条件,则执行其他行为,如随机移动行为
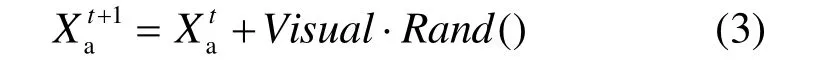
2) 聚群行为:设人工鱼的当前状态为aX,探测其邻域的伙伴数目nf,如果表明伙伴中心有较多的食物且不太拥挤,并且Ya>Yc,则向中心位置Xc前进一步,为

否则,执行其他行为(如觅食行为)。
3) 追尾行为:设人工鱼当前状态为 Xi,探测其邻域内状态最优的邻居 Xmax,如果,并且Xmax的邻域内伙伴数目nf满足< 1 ),表明 Xmax附近有较多的食物且不太拥挤,则向 Xmax的方向前进一步,为
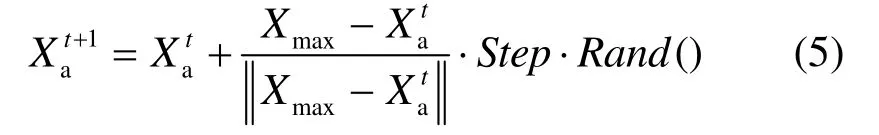
否则执行觅食行为。
4) 随机行为:人工鱼在视野范围内随机选择一个状态,然后向该方向移动,其实是觅食行为的一个默认缺省行为
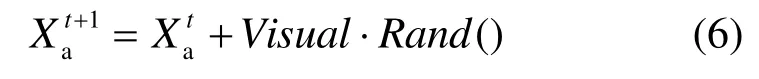
5) 公告板:主要用于记录优化过程中最优人工鱼个体的状态。
3 改进人工鱼群算法求解最短路径问题的原理
3.1 基本人工鱼群算法求解最短路径问题的缺陷
从人工鱼的基本行为算法描述中可以看出,视野在寻优过程中是非常重要的。在反复的实验过程中发现,参数视野固定不变,导致算法后期收敛速度慢,且算法的计算量较大;当路网的节点数目较大时,甚至陷入局部最优,无法搜索到全局最优解。
因为在参数视野不变的情况下,当人工鱼逐渐逼近最优解时,只有很少的人工鱼状态不同于最优解的人工鱼状态,所以,人工鱼在最优解附近以原始的视野进行觅食是盲目的。在这种情况下,当给定的视野很大,算法的前期收敛很快,但后期收敛很慢,且Trynumber的试探次数会很大,增加算法的计算复杂性;如果给定的视野很小,则会使收敛变慢,计算量大,甚至陷入局部最优。这将降低最短路径搜索效率和准确性。
3.2 解决的办法
为了解决上述问题,提出视野自适应的人工鱼群算法(AVAFSA,artificial fish-swarm algorithm based on adaptive vision)。
由于人工鱼的觅食行为是算法收敛的基础,所以聚群行为和追尾行为的视野保持不变,只对觅食行为的视野改进,采用自适应的视野,在算法的初始阶段,给觅食行为一个较大的视野,随着算法的迭代进行,逐渐减小视野。
但是,经测试发现,当算法后期的视野太小,算法搜索到全局最优解的概率会变小。所以,在该视野自适应的改进人工鱼群算法中,当视野的当前值小于初始值的一半时,停止减小,使其保持为初始值的一半(当然也可以根据具体问题设置参数视野值的下限)。算法的表达式为

3.3 自适应视野人工鱼群算法最短路径实现原理
人工鱼群算法是求解 TSP问题的一个有效方法,而TSP问题与指定起点到目标点的静态最短路径问题的相同点是:两者都属于组合优化问题。区别在于:TSP的每一种路径都要遍历所有的城市,而指定 2点间的最短路径问题不需要遍历每个节点。所以,本文在人工鱼群算法求解最短路径问题中,借鉴了文献[10]中人工鱼群算法求解TSP的编码方式,但算法模型有2点不同。
1) 目标函数:从起点到目标点所经过的路径段的道路权重(经济、时间、距离的加权组合)求和。若某条人工鱼所代表的路径(以6个网络节点为例)为:N4、N1、N2、N3、N6、N5,要求的路径为起始节点1到终点节点6的最短路径,则该人工鱼的目标函数
2) 新路径的产生
(a)交换节点与节点在路径序列中的位置,将得到新的路径;
(b)从起点到目标点所经过的节点数目不同,也将产生新的路径。
3.4 改进人工鱼群算法求解最短路径问题的步骤
算法的实现步骤如下。
1) 输入原始数据,获取路网节点数 P o i ntNum、各节点的具体坐标位置 P o i ntP osition[]、节点的权值矩阵 e dge[]、获取人工鱼群的群体规模FishNum、最大迭代次数 I terate_times、人工鱼的视野初始值Visual、最多试探次数Trynumber、人工鱼的最大移动步长Step、拥挤度因子δ等参数。
2) 当前迭代次数 P assed _ t imes= 0 ,生成FishNum个人工鱼个体,形成初始鱼群,每一个人工鱼代表从起点到目标点的一种路径,即从起点至终点的随机序列。
3) 各人工鱼分别模拟执行觅食行为、追尾行为和聚群行为;选择最优行为执行,缺省行为方式为觅食行为。
4) 各人工鱼每行动一次后,检验自身状态与公告牌状态,若自身状态优于公告牌状态,则以自身状态取代公告牌状态。
5) 终止条件判断。判断 p assed _ times是否已达到预置的最大迭代次数 I terate_times,若是,则输出计算结果(公告牌的值);否则, P assed _ times=Passed _ t imes+ 1,转步骤3)。
4 算法的仿真
4.1 道路网拓扑结构
某道路网的无向赋权拓扑如图1所示,路网中共有9个节点。用 wi,j(t)表示每一路段的非负权值,静态环境下,常数,表示从节点 vi出发到达节点 vj所需要的行驶代价(时间或费用),若路段(vi, vj)不连通,则其权重,同一个节点的权重为
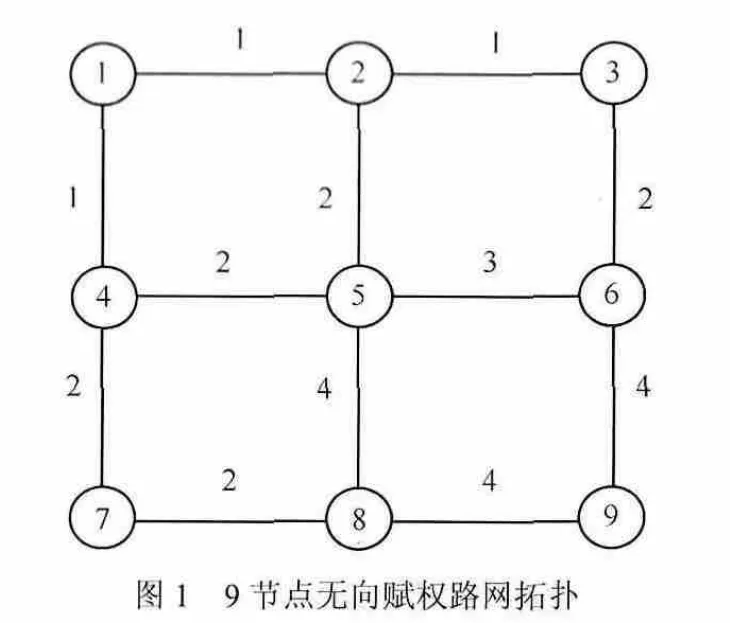
图1 9节点无向赋权路网拓扑
则路网中的权重可用矩阵表示为

4.2 仿真结果与数据分析
9节点路网拓扑图如图1所示,假设起点为节点1,终点为节点9,权重矩阵如式(8)所示,则利用人工鱼群算法计算这2点间的静态最短路径。
现在将对上述改进型的自适应视野人工鱼群算法求解最短路径方法进行仿真,并与基本人工鱼群算法及蚁群算法优化结果进行对比。仿真环境为:Pentium(R)Dual-Core,2.19 GHz,2.00 G内存的计算机。仿真工具为: Matlab R2010a。参数路阻∞=100,人工鱼群算法参数:人工鱼数目FishNum= 1 0,最大迭代次数 I terate_ t imes= 2 00,最大试探次数 T rynumber= 1 00,初始化视野 V isual=5(根据节点数给定),拥挤度因子deta = 0 .8。蚁群算法参数:最大迭代次数 N cMax= 2 00,蚁群规模m=10,留在每个节点上的信息量受重视程度α=0.1,启发式信息受重视程度β=2,信息的保留率ρ=0.1。
因为蚁群算法、基本人工鱼群算法和自适应视野的改进人工鱼群算法最终都以 100%的成功率搜索到了全局最优解,所以图2给出改进算法求得的最短路径。所求的最优解为 8,得出的路径为1→2→3→6→9→8→4→7→5;其中 1→2→3→6→9为所求的从起点1至目标点9的最短路径。
图3为9节点路网中基本蚁群算法、基本人工鱼群算法及自适应视野的改进人工鱼群算法的寻优过程对比。3种算法分别在第2次、5次、3次迭代后搜索到全局最优解。可以看出改进鱼群算法比基本鱼群算法的收敛速度快。蚁群算法虽然以最快速度搜索到最优解,但搜索过程中出现“之”字形路径,不稳定。

图2 视野自适应人工鱼群算法(AVAFSA)搜索的最短路径
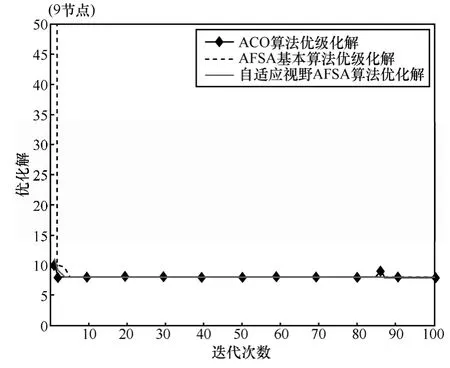
图3 ACO、基本AFSA与改进的AVAFSA收敛曲线
下面重点对3种算法的计算量和收敛速率进行比较,仿真环境和初始条件不变,对比实验结果如表1所示。
表1对3种算法各取5次仿真实验数据,其中,BEST_GEN表示算法首次搜索到最优解的迭代次数,BEST表示最优解(即最短路径总长度),TIME表示算法迭代200次花费的时间。分析表1的实验数据,可以明显地看出,基本蚁群算法在求解简单路网的最短路径时,速度还是很快的。改进人工鱼群算法比基本人工鱼群算法的运算量小,收敛性好。也验证了自适应视野改进算法的可行性和高效性。

表1 9节点ACO、AFSA及AVAFSA算法的对比实验结果
为了验证算法的高效、稳定性,假设路网更复杂些,抽象为 16节点的赋权无向图,其道路权重的邻接矩阵为

图4为改进的自适应视野人工鱼群算法得出的16节点静态最优路径为7→4→3→2→12→14→1→5→9→10→11→15→16→6→13→8,其中,1→5→9→10→11→15→16为所求的从起点1到终点16的最短路径。最优值为19。

图4 视野自适应人工鱼群算法(AVAFSA)搜索的最短路径
图5 为16节点路网中,基本蚁群算法、基本人工鱼群算法及自适应视野的改进人工鱼群算法的寻优过程对比。可以看出蚁群算法由于没有方向性引导,在路网变复杂时,搜索过程中的“之”字形路径现象更严重;又因为其概率性和正反馈作用,使算法陷入了局部最优,最终不能得到全局最优解。基本人工鱼群算法在迭代93次后得到全局最优解,而改进人工鱼群算法在迭代35次后就得到全局最优解。显然,改进的自适应视野的人工鱼群算法比基本鱼群算法的后期收敛速度快,而且,路网越复杂(节点越多),该改进算法的优势越明显。
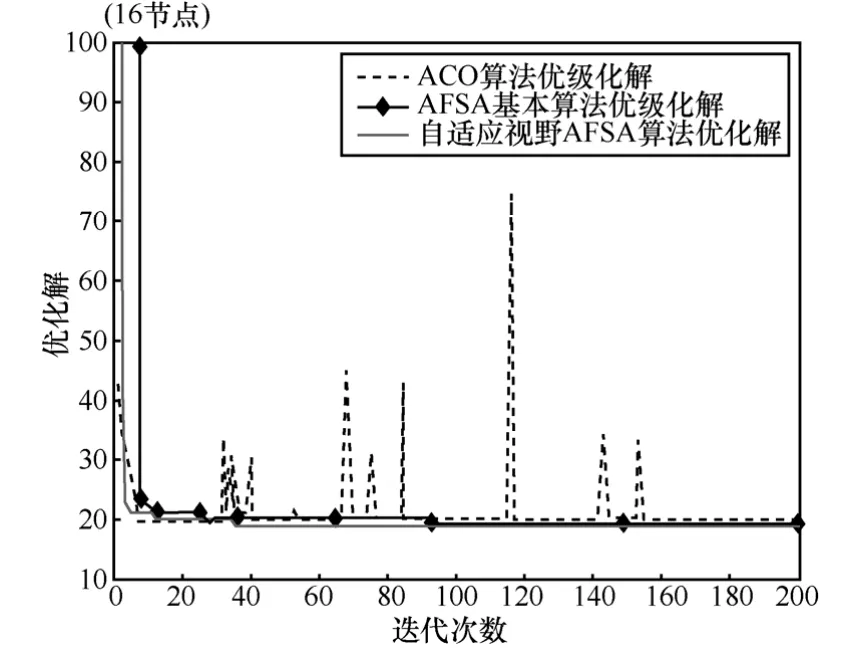
图5 ACO、基本AFSA及AVAFSA收敛曲线
下面对ACO、AFSA和AVAFSA的计算量和收敛速率进行比较,仿真环境和初始条件与上面的 9节点完全相同,对比实验结果如表2所示。
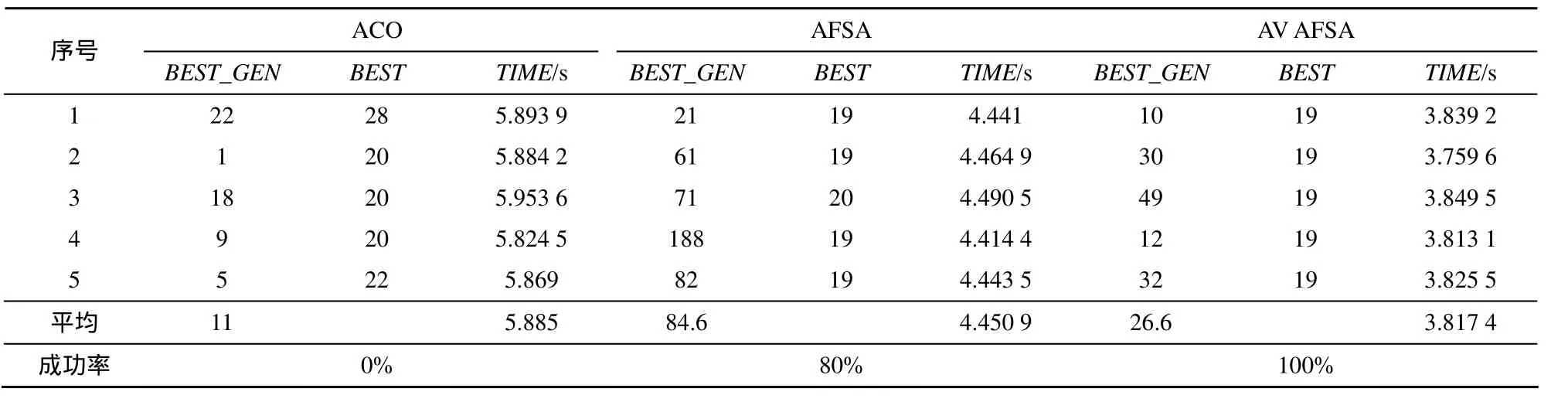
表2 16节点ACO、AFSA及AVAFSA算法的对比实验结果
从表2可以明显地看出,基本蚁群算法在路网复杂时,搜索不到全局最优解,只能得出较优解,而且算法时间复杂度明显增加。而本文视野自适应的改进人工鱼群算法比基本人工鱼群算法收敛速度快、运算量小,而且准确性高。与表 1对比,得出路网越复杂,该改进算法的优越性越突出,说明该改进算法是一种高效、稳定的最短路径求解方法。
5 结束语
针对基本人工鱼群算法因参数视野固定不变而导致算法后期收敛速度慢、运算量大、陷入局部最优的缺陷,本文根据车辆导航系统中的静态最短路径问题的特点,对人工鱼群算法进行了改进。该改进算法只对人工鱼的觅食行为的视野进行调整,使其随着迭代次数的变化而自适应地变化,并设置了视野值的下限,以防视野过小,算法又陷入局部最小。实验结果表明,改进型人工鱼群算法的收敛速度、计算量、寻优精度和准确性均优于基本蚁群算法及基本人工鱼群算法,而且道路越复杂,节点越多,这种优势越显著。
[1] 孙中华. GIS路径寻优中的蚁群算法研究[D]. 南京: 南京理工大学,2009.SUN Z H. Research on Ant Colony Algorithm in GIS Path Optimization[D]. Nanjing: Nanjing University of Science and Technology, 2009.
[2] 谭国真, 高文. 时间依赖网络最小时间路径算法[J]. 计算机学报,2002, 25(2):165-172.TAN G Z, GAO W. The minimum time path algorithm of the time-dependent network[J]. Chinese Journal of Computers, 2002,25(2):165-172.
[3] 王海梅. 基于 GIS的最优路径算法研究与实现[D]. 南京: 南京理工大学, 2008.WANG H M. Research and Implementation of the Optimal Path Algorithm Based on the GIS[D]. Nanjing: Nanjing University of Science and Technology, 2008.and Technology, 2008.
[4] 甘荣伟. 蚁群优化算法及其应用研究[D]. 广州: 中山大学, 2009.GAN R W. Research on Ant Colony Optimization and Its Application[D]. Guangzhou: Sun Yat-sen University, 2009.
[5] 张学敏, 张航. 基于改进蚁群算法的最短路径问题研究[J]. 自动化技术与应用, 2009, 28(6):4-7.ZHANG X M, ZHANG H. Research on the shortest path problem based on an improved ant colony algorithm[J]. Automation Technology and Application, 2009, 28(6):4-7.
[6] 潘海珠, 杜晓昕, 王波. 基于人工鱼群的交通诱导系统最优查询研究[J]. 齐齐哈尔大学学报, 2012,28(5):6-9.PAN H Z, DU X X, WANG B. Research on the optimal query research of traffic guidance system based on artificial fish-swarm algorithm[J].Journal of Qiqihar University, 2012, 28(5):6-9.
[7] 郑根让. 基于混合人工鱼群算法车辆拥堵调度方案[J]. 计算机仿真, 2012, 29(6):328-331.ZHEN G R. Vehicle congestion scheduling scheme based on a mixed artificial fish-swarm algorithm[J]. Computer Simulation, 2012, 29(6):328-331.
[8] 李晓磊, 邵之江, 钱积新. 一种基于动物自治体的寻优模式:鱼群算法[J]. 系统工程理论与实践, 2002, 22(11):32-38.LI X L, SHAO Z J, QIAN J X. An optimization mode based on Autonomous: fish-swarm algorithm[J]. Systems Engineering Theory and Practice, 2002, 22(11):32-38.
[9] 李晓磊. 一种新型的智能优化方法—人工鱼群算法[D]. 杭州: 浙江大学, 2003.LI X L. A New Type of Intelligent Optimization Method: Artificial Fish-swarm Algorithm[D]. Hangzhou: Zhejiang University, 2003.
[10] 江铭炎, 袁东风. 人工鱼群算法及其应用[M]. 北京: 科学出版社,2012.JIANG M Y, YUAN D F. Artificial Fish-swarm Algorithm and Its Application[M]. Beijing: Science Press, 2012.

