基于二次独立集的数据融合调度算法

许建，杨庚，陈正宇，王海勇，杨震

(1. 南京邮电大学 宽带无线通信与传感网技术教育部重点实验室，江苏 南京 210003；

2. 南京邮电大学 计算机学院，江苏 南京 210003；3. 金陵科技学院 信息技术学院，江苏 南京 211169)

1 引言

无线传感器网络由具有感知能力、存储能力和通信能力的无线节点组成，大多数情况下节点在资源方面受到很多的限制，其中最为突出的是节点能量方面的受限。因此，如何降低节点的能耗，延长网络节点的生命周期成为无线传感器网络应用的关键问题。

在传统的无线网络中，媒体访问控制协议（MAC）是决定网络生命周期的关键因素，这一点对于无线传感器网络同样适用。现有的传感器网络MAC协议基本上可分为2类，基于竞争的访问控制协议和时分复用的访问控制协议。其中，基于竞争的访问控制协议，如IEEE 802.11，在冲突处理和监听过程中会浪费大量的能量消耗。而对于TDMA协议来说，节点按照预先分配的传输时隙进行数据的发送和接收，在避免了由于冲突而造成能量消耗的同时也保证了数据聚集过程的时延[1]。文献[2]中对2种MAC协议下的网络生命周期进行了测试，相同条件下TDMA协议的能耗仅为IEEE 802.11协议的约1/120，可见TDMA协议在降低能耗方面要显著优于基于竞争的访问控制协议。

另一方面，数据融合技术也是降低节点的能耗，延长网络生命周期的重要手段。数据融合是多跳网络中数据聚集和路由的一种方式，其特点是数据采集的中间节点在收到不同信息源的数据后，以去除冗余信息为目的对所接收到的多个数据进行融合处理，进而能够实现减小传输数据量，降低节点由于大量数据传输而带来的能量消耗，延长网络生命周期[3]。

综合以上2个方面，在数据融合聚集的过程中采用TDMA为MAC层协议，可以从不同层次减少节点的能量消耗。在时分复用的无线传感器网络中，数据融合技术的关键在于融合调度策略，衡量融合调度算法有效性主要体现在以下3个方面。首先通过合理调度降低由于冲突而造成的网络传输时延增加；其次，由于多次通信和融合操作会造成网络中节点能耗的增加，融合调度过程应该尽可能地减少调度次数，并实现节点间能量消耗的平衡，进而延长网络的生命周期；第三，加权公平性保证，即对于具有不同权重的数据应该区别对待，保证高优先级的数据优先调度。然而，现有算法大多仅针对其中的某一个方面进行了相应研究。如文献[4,5]主要从融合树构建的角度分析了如何进一步降低融合过程的能量消耗、延长网络的生命周期；文献[6~8]从降低融合过程时延的角度对基于 TDMA的数据融合调度算法进行了研究，并分别提出了不同的低时延调度策略；而文献[9]则单纯考虑加权公平性，并没有涉及其与另外两方面性能的平衡。总体来说，这些研究成果均没有综合考虑3个方面的因素，因而各自具有不同的局限性。

针对上述不足，本文从调度算法的3个有效性指标入手，通过分析融合树结构以及调度算法对各方面性能的影响，提出了一种基于二次独立集的TDMA融合调度算法 MISS(twice maximum independent set based aggregation scheduling algorithm)。该算法由 2个子算法组成：基于最大独立集的数据融合树构建算法(T-MIS)和基于最大独立集的数据融合调度算法(S-MIS)。T-MIS以最大独立集方法构建树型结构，并根据节点能量消耗预测模型对树结构进行调整和优化，最终构造出能量消耗平衡的数据融合树。S-MIS根据融合树中的链路冲突关系构建近似最大加权独立集，最终确定每个时隙中的传输链路序列；并在该过程中，重点研究了不同链路权重参数设置下融合调度策略的调整方法。

2 问题描述

1) 所有节点采集的数据均被汇聚到sink节点；

本文中对于冲突的定义，采用协议冲突模型[10]，约定网络中任意节点均可以发送和接收数据，但二者不能同时进行，且所有节点的干扰半径均相同，记为Ir。

定义1 链路冲突。在协议冲突模型中，2个通信链路冲突，当且仅当其中一个链路的接收端在另一个链路发送端的干扰半径范围内。

如图1所示，节点j的父节点jP在节点i的干扰半径范围内，则通信链路ie和je是相互冲突的。

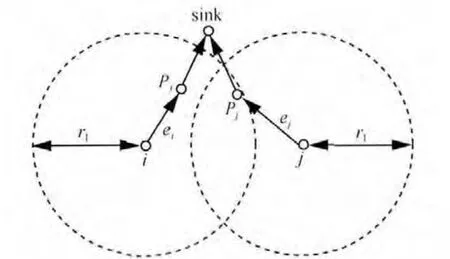
图1 链路间冲突关系

根据引言中的分析，构造出的调度序列应该尽可能同时满足3个方面的特性需求。相关定义如下。

定义2 融合时延。对于一次数据聚集过程，若所有节点采集的信息经过 t个时隙后全部到达 sink节点，即，则该融合周期的时延为t，记做

对于任意结构的数据融合树，其融合延时有

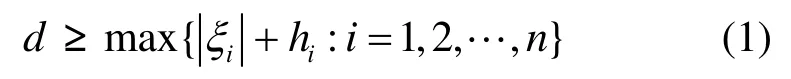
其中，ξi和hi分别表示节点i在该树中子节点的个数以及该节点到树根节点的跳数，Baljeet等人在文献[11]中对该问题予以了证明。

由于传感器节点所监测区域的重要性不同，每个节点被分配一个反映其重要性的权值，节点i的权重值表示为 wi。直观地，如果 wi＞wj，则希望i节点采集的数据能够比 j节点采集的数据更早到达sink节点。为了量化这种加权公平性，本文使用平均加权时延作为公平性度量，其定义如下。

定义 3 平均加权时延。在一个融合周期内，若G中节点i采集的数据共经历了 ti个时隙后到达sink节点，则该节点数据的加权时延为 Di= wi× ti，融合周期内所有节点的平均加权时延可计算为

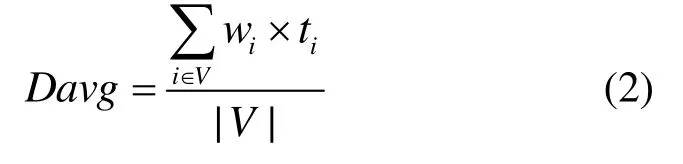
图2为一种平均加权时延计算示例，图2(a)中给出了一个由3个节点组成的数据融合树，其中，；图 2(b)对 2种可能调度序列下的avg分别进行了计算。在第1种调度序列中，t1和 t2分别为1和2，所以；同理，若调度序列为{e1} }，则 D avg= 2 .5。显然，即使这2种不同调度策略具有相同的融合时延，但其对加权公平性的保证也可能是不同的。

图2 平均加权时延计算示例

定义4 网络生命周期。对于任意调度算法，若经历了L个融合周期后网络中出现了第一个能量耗尽的节点，则称该调度算法下的网络生命周期为L。

在基于TDMA机制的数据融合过程中，节点主要有3种不同状态，发送、接收和睡眠，其中，睡眠状态下的功耗远远小于其他2种状态[12]，文中将该状态下的能量消耗忽略不计。此时，每个融合周期内节点 i的能耗可计算为，其中， pt、 pr分别表示节点进行一次发送和接收的能耗，ti和 ri则表示节点i发送和接收的次数。假设所有节点具有相同的初始能量EN，则对于任意的数据融合树其生命周期可表示为

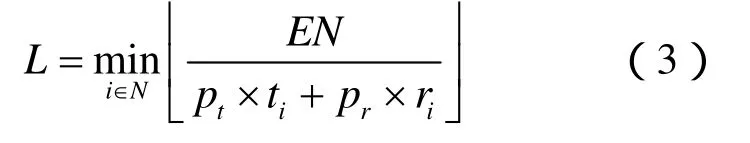
从以上对3种性能的定义和分析可以看出，融合算法的性能主要和融合树结构以及调度策略有关。因此最优的融合调度即通过以上2个步骤构造出调度链路集合序列实现min(d)、min(D avg)以及max(L)3个方面性能平衡。因此，本文提出的MISS算法分为融合树构建和融合调度2个阶段，其具体实现过程将在接下来分别进行阐述。

3 基于最大独立集的数据融合树构建算法T-MIS

3.1 算法思路

融合树的构建是数据融合过程的准备工作，在所有基于树的数据融合过程中均需要预先建立起一个融合树结构。之所以选择树型结构，主要有2个方面的原因：首先无线传感器网络中仅有一个或极少量基站节点，树结构很适用于这一类型的网络环境中；另一方面，树结构自身的特点有助于节省传输中的能量开销，这对于能量受限的无线传感器网络来说尤为重要[9]。然而最优融合树构造已被证明是NP-hard问题[13]，现有的融合树构建算法均是从某一方面出发的近似优化算法，主要焦点集中在如何延长网络生命周期或降低融合时延等。从现有的研究成果分析，融合树对生命周期和时延性能的影响主要包括2个方面因素，树中节点的度数以及树的深度。

文献[14]中提出了一种融合树构建算法。该算法通过最大独立集构造出最小连通支配集，并以该支配集为树干生成树结构。由最小连通支配集的定义可知，该树结构具有叶子节点最多而树的深度最小等特性，从而可以增加节点间并发通信的几率，减少中间转发次数，进而降低融合时延。但该算法并没有考虑节点的能耗平衡，容易产生由于局部节点能量耗尽而导致的网络生命周期缩短。无线传感器网络中节点处理器执行指令的能耗远小于数据传输的能耗，节点的能量消耗主要取决于其发送和接收数据的次数。为了减少能量消耗，往往会限制节点发送数据的次数，此时子节点最多的节点将成为整个网络中能量最先耗尽的瓶颈节点，显然为了延长网络的生命周期必须实现树中节点的度数平衡。为此，T-MIS在构造出该树型结构后，再根据节点的能量消耗预测对树结构进行调整。能量消耗预测指的是根据节点在树中的位置对其在融合过程中可能消耗的能量进行的估计。

3.2 算法描述

算法1 数据融合树构建算法T-MIS。

1) 以 vs为根，r为网络半径，构造G的广度优先搜索树；

2) 对所有vi∈V，C(i)=White，Mark(i)= 0 ，

4) 对于收到 M esg(B)节点 vj，如果则，广播 M esg(G)；

5) 对于 vj，如果，且所有 vi,且，都向其发送了 M esg(G)，则，广播 M esg(B)；

7) 根节点 vs广播 M esg(Gjoin)；

8) 对于收到 M esg(Gjoin)的节点 vi，如果且vi∉DS

② 广播 M esg(Bjoin)；

③ M ark(i)=1；

9) 对于收到 M esg(Bjoin)的节点 vi，如果Mark(i) = 0，C(i)=Black且vi∉DS

① vi→DS（Pi为Mesg(Bjoin)的发送节点）；

② 广播 M esg(Gjoin)；

③ M ark(i)=1；

10) 以DS为树干，其余节点为叶节点（ Pi为其支配节点）形成树结构；

11) 对所有非根节点vi∈V，标记其子节点个数为

该算法中首先构造G的广度优先搜索树，若节点 i所在的层数为 leveli，则标记 R (i) = ( l e veli,i )；算法经过前 5个步骤后，所有黑色节点构成一个支配集，即然后通过步骤7)~10)构造出一个连通的树型结构；最后对所有非根节点选择子节点最少的上层节点为父节点，形成最终的数据融合树，记为。图3为T-MIS算法的执行过程示例。如图3(a)所示，该网络中共有15个节点，其中，sink节点s位于网络的拓扑中心。算法中首先通过构造最大独立集(MIS)的方法形成网络的最小连通支配集(图 3(b)中的灰色节点)；以该连通支配集为树干，连接形成树型结构如图3(c)所示；最后，根据能量消耗预测进行调整，最终形成一个平衡融合树如图3(d)所示。

4 基于最大独立集的数据融合调度算法S-MIS

4.1 算法思路

调度算法的最终目的是为节点分配传输时隙，本文提出了基于近似最大加权独立集的调度算法，其主要过程分为 2个步骤。首先，选中树中允许通信的链路集合，通过融合树结构中链路间的冲突关系，构建链路冲突矩阵，然后在冲突矩阵的基础上，通过构造近似最大加权独立集确定每个时隙中的通信链路集合。特别要强调的是，已有算法中，为了最大程度降低节点的能耗，都采用了每个链路仅调度一次的限制策略，但是这种策略无法保证对高权重数据的优先调度（即加权公平性保证）。但如果对链路的通信次数不做任何限制又会造成网络能耗的急剧增加，可见如何调整通信次数是在低加权时延和高生命周期之间实现性能平衡的关键。为此，S-MIS算法采取了折中的调度策略，相关定义如下。

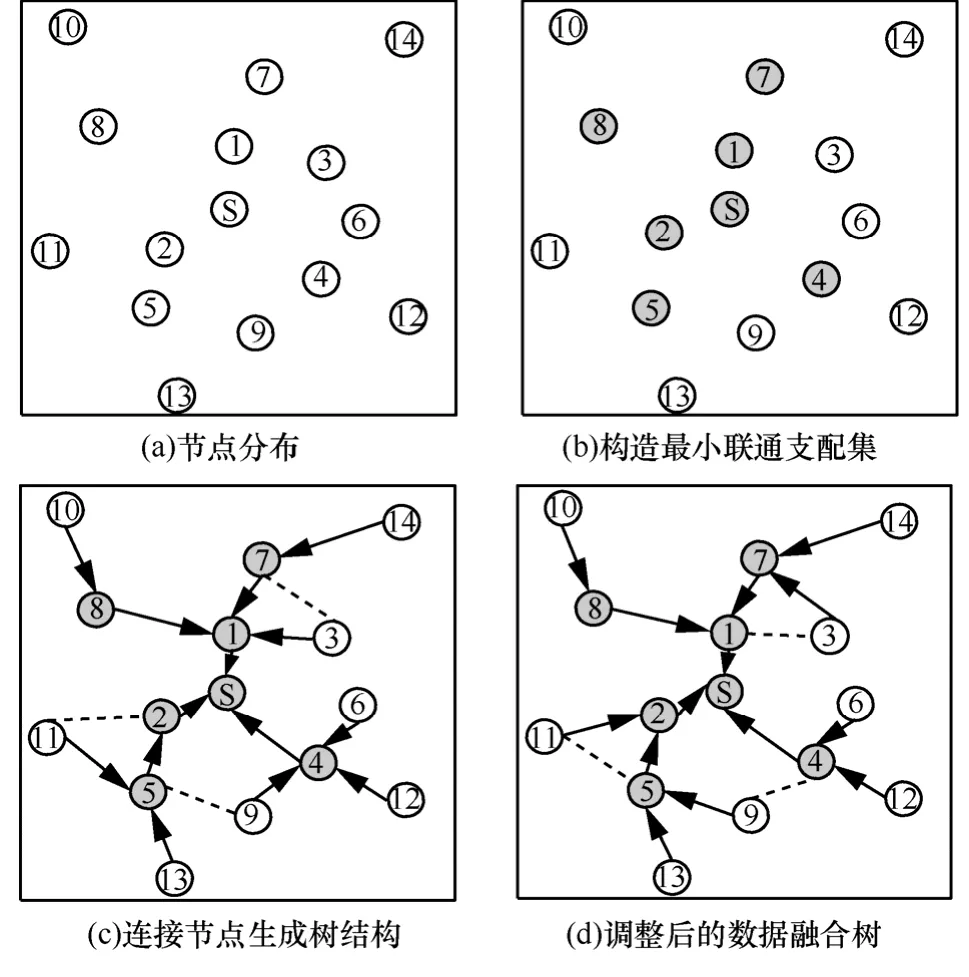
图3 数据融合树构建过程

定义5 边沿链路集。对于树 T = ( V,Eˆ)，若经历t-1个时隙后，节点vi的所有子节点均被调度完毕，则以vi为发送端的链路ei为t时刻树T的边沿链路，记 F LS(T )t为t时刻树中所有边沿链路的集合。

图4中给出了2个不同时隙内边沿链路集选取的示例。在t=1时，树中所有以叶子节点为发送端的链路均为边沿链路，即当经过n-1个时隙后，黑色节点均被调度完毕，此时有

定义6 累积权重。对于 ei∈Eˆ，t时隙中，节点i中仍未被传输数据的权重之和称做该链路上的累积权重，记做 A CW(ei)t。

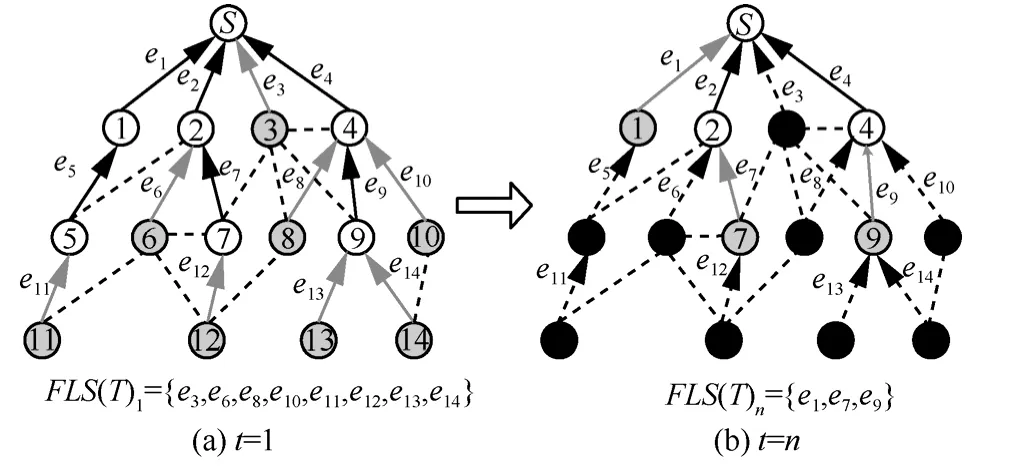
图4 不同时隙内边沿链路集的选取

定义7 激活链路集。时隙t中可以作为调度对象的链路集合，包括边沿链路以及累积权重达到阈值 δ的非边沿链路，记 t时刻的激活链路集合为ALS(T )t，则

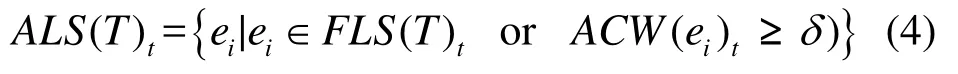
定义 8 冲突链路集。对于不在链路集合 Et中的 ei，若 ei和 Et中的n个链路冲突，则称这n个链路组成的集合为 Et中 ei的冲突链路集，该集合中所有链路权重的和为 ei相对于 Et的冲突集权重。

在限定链路通信次数的调度算法中，仅将边沿链路作为调度的对象，所以即使出现了需要优先调度的中间链路，在其成为边沿链路之前均得不到调度。而S-MIS中，将激活链路集作为调度对象，通过设置阈值δ将高优先级的中间链路纳入到调度对象中，并可以通过对δ的调整实现加权时延和能量消耗之间的性能平衡。以图4(b)中的调度对象为例，假设，则

除了通过选取激活链路作为调度对象外，为了保证对高权重数据的优先传送，本文希望能够构造出每个时隙内激活链路集合的最大加权独立集作为该时隙内的调度序列，但由于该集合的求解过于复杂，本文提出了一种构造最大加权独立集的近似算法。

4.2 算法描述与分析

算法2 数据融合调度算法S-MIS。

2) 对每个标记为未调度的链路 ei，如果 ei∈FLS(T )t或，则

3) 构造 A SL(T )t中链路的冲突矩阵 I Mt，若ASL(T )t中第i和j个链路在T中冲突，则

4) 构造以 I Mt为邻接矩阵的最大独立集MISt；

5) 对于所有不在 M ISt中的激活链路 ej，若 ei未调度则以其累计权重从高至低进行如下操作：

若 A CW(ei)t大于其相对于 M ISt的冲突集权重，则在 M ISt中以 ej取代其冲突链路集，构造出近似的最大加权独立集 M WISt；

8) 如果 DAT中仍有标记为未调度的链路，则t = t + 1，转至步骤2)；

算法2的输出结果即为每个时间片中传输的链路集合，该集合必满足以下3个条件：

2) 每个节点采集的数据均到达sink节点；

证明 首先，对于DAT链路集合Eˆ中任意元素ei，显然有 ei∈Eˆ。若算法执行完毕后仍然有链路有，则经过t个时隙后，DAT中仍有未调度的链路，与题设矛盾，因此必有另一方面，对于任意链路，则ej必是DAT中的一个边，即有 ej∈Eˆ。因此，必有∪ E (t )。

其次，采用反证法。假设融合周期结束后节点 i上仍有数据没有被汇聚到sink节点。若该节点为DAT中的叶子节点，则表明由前面证明可知与题设矛盾，即 i只可能为中间节点。不妨设在第次调度后，该数据到达中间节点 i，则链路 ei在前面的 m - 1次调度中均不可能被标记为已调度，而由假设前提可知此后 ei也未被调度（数据依然在节点 i中），则同样有综上，调度完毕后必能保证所有节点的数据都被汇聚到sink节点。

最后，对于调度序列集合中的 E (s)(1 ≤ s≤t)，由算法2可知，该集合为s时刻以 I Ms为邻接矩阵的最大加权独立集，若，则IMs中对应元素，因此 ei, ej必然彼此不冲突。

证毕。

5 实验结果与分析

在本节中，对MISS算法进行了仿真实现，并将其性能和已有算法DAS[7]、IAS[8]等进行了比较。表1中给出了仿真参数设置。在实验中，节点随机均匀的分布在200 m×200 m的区域中，假设基站节点 sink位于区域的拓扑中心。彼此间距离小于等于通信半径r的2个节点可以相互通信；相互间不冲突的多个链路可以同时通信，本文实验中将干扰半径取值为Ir r= ；所有节点具有相同的初始能量EN=1 000，为了不失一般性，参考文献[15]中的测量结果，将节点进行一次发送和接收所消耗的能量分别取值为 Pt=2，Pr=1；节点的权重为 0～10之间的随机数。

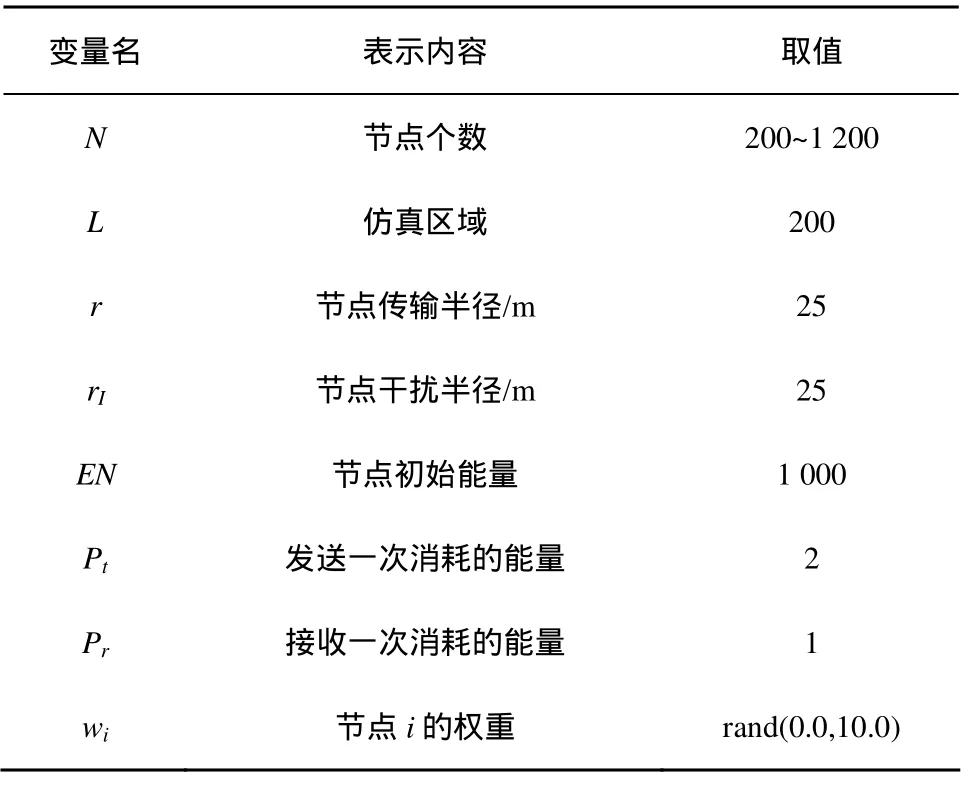
表1 仿真参数设置

为了全面深入地对算法性能进行比较分析，本文共设计了3组不同的仿真实验，每组中均对算法在融合时延d，平均加权时延Davg以及生命周期L 3个方面的性能进行了比较。实验中对于节点密度ρ的定义采用和文献[11]相同的表示方法，即，在通信半径相同的情况下，节点数量是影响密度的唯一因素。

由于现有调度算法大多没有考虑节点权重的因素，为了和这些算法进行性能比较，第一组实验中首先假设所有节点的权重均为 1，此时累计权重ACW(ei)t表示t时刻节点i中未传输的数据个数。并设置MISS算法中阈值δ为节点个数N，融合过程中没有中间链路能够被调度，即限制每个节点均只能发送1次。图5~图7为第一组实验中算法在不同节点密度下的性能比较。

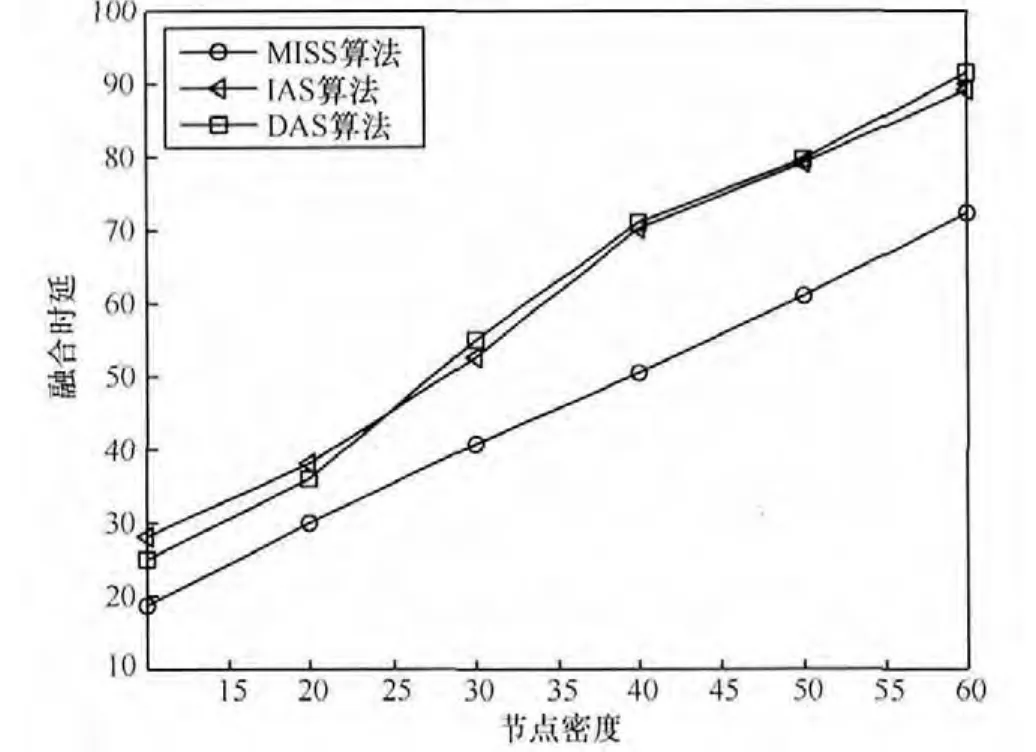
图5 算法融合时延随节点密度变化比较

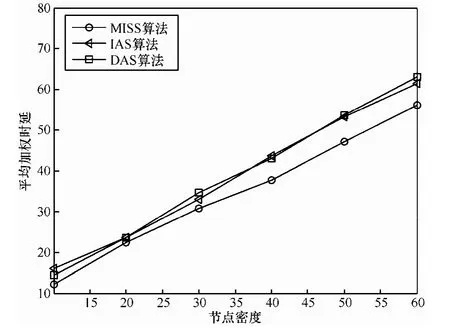
图6 算法平均加权时延随节点密度变化比较

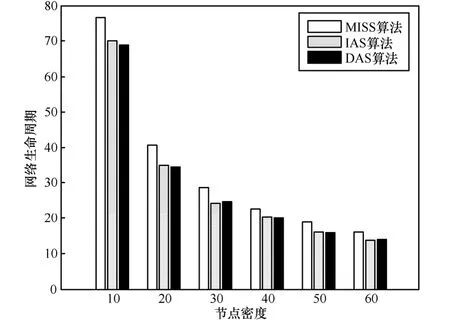
图7 网络生命周期随节点密度变化比较

由图5中的变化曲线可以看出，由于节点密度增大后，节点间冲突程度增加，所以3种算法的融合时延均随着节点密度有较大幅度的增加。IAS算法和 DAS算法在时延方面的性能相差不大，本文提出的MISS算法相对于这2种算法来说优势较为明显。当节点密度从10增加到60时（节点个数约从 200增加到 1 200），前 2种算法的时延从约25个时隙增加 90左右，相同情况下 MISS算法仅从18增加到了 72。时延性能提升的主要原因在于本文算法通过构造最大独立集的方式选取每个时隙中的发送序列，能够在每个时隙中实现最大并发度的通信，从而更快地完成数据汇聚过程。

算法的平均加权时延同样随节点密度的增加而增大，其结果如图6所示。由于本组实验中假设将节点权重设置为1，所以3种算法在加权时延方面差异并不明显。MISS算法由于能够找出最大可传输集合，其平均加权稍优于另外2种算法。

图7则给出了网络生命周期随节点密度增加时的变化情况。首先可以看出，在节点传输半径不变的情况下，随着节点密度的增加，开始阶段网络生命周期迅速减少，如ρ从10变为20时，3种算法下的生命周期几乎均减少了一半，但随着节点密度的进一步增加，生命周期下降的速率变得逐渐缓慢。从第2节中对网络生命周期的定义和分析可以知道，出现这种情况的主要原因在于，ρ从10变为20时树中节点的最大度数几乎增加了一倍；而当节点不断增加时，节点度数虽然还在增加但增加的比例降低了，因此生命周期会出现图中所示的变化过程。值得一提的是，虽然此时3种算法都限定了节点的发送次数为1次，但是由于 MISS在构建数据融合树时根据节点的能量消耗预测进行了调整，因此其生命周期要略高于IAS和DAS。

在第2组实验中对算法在节点具有不同权重下的各方面性能进行了比较，其中MISS算法中阈值分别取值为 0、40和无穷大，实验结果如图 8~图10所示。

图8中对MISS算法在δ=0、δ=40以及δ=无穷大时融合时延性能同DAS、IAS算法进行了比较。从该图中可以看出，当δ=0时，表示所有中间链路均可成为激活链路，MISS算法中会选择权重较大的中间链路进行调度，使得此时的融合时延明显增大。而当δ=无穷大时则表示不允许任何中间节点进行权重比较和替换，此时的融合时延在各种算法中为最优的。δ取中间值时，如δ=40，算法的融合时延也处于中间位置。对于DAS和IAS算法来说，由于它们均没有在调度算法中考虑加权因素，所以其性能和第一组实验基本相似。

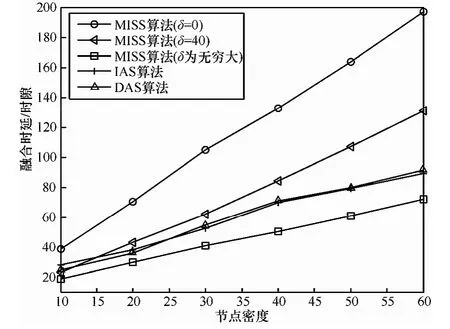
图8 节点具有不同权重时融合时延随节点密度变化比较

图9 中则对比了第2组实验中不同算法的平均加权时延。由于本文算法MISS中以阈值δ来筛选出权值达到一定限制的中间链路来进行优先调度，所以此时MISS算法能够很好地实现加权公平性保证，即优先调度那些权重更高的节点。但是如果将δ取值为 0，则会有太多的中间链路参与调度，将会导致融合时延的迅速增加（如图 8所示），最终使得加权时延性能也随之下降。通过对比实验数据，当节点密度小于20时，加权时延对阈值δ并不敏感，节点密度大于20后，δ=40下的MISS算法具有最低的平均加权时延。

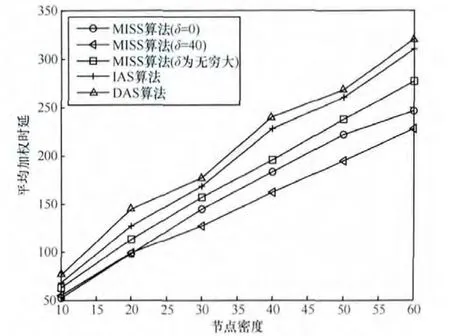
图9 节点具有不同权重时平均加权时延随节点密度变化比较

当节点具有不同的调度权重时，MISS算法调整调度对象后同样会造成网络生命周期的降低，如图 10所示。同前面的分析类似，当阈值为无穷大时，每个节点仅能够发送一次数据，此时的网络生命周期最长，虽然IAS和DAS也限定了发送次数为1，但由于这2种算法中均没有考虑节点能耗的平衡问题，所有生命周期小于阈值足够大的 MISS算法。随着对节点通信次数限制的放宽（主要通过调整δ），节点的能耗也会明显的增加，最终导致网络生命周期的减少。显然δ越小，限制条件也就越松，节点通信的次数也就越多，进而网络生命周期也就越短，如图10中所示δ等于0时网络的生命周期最短。

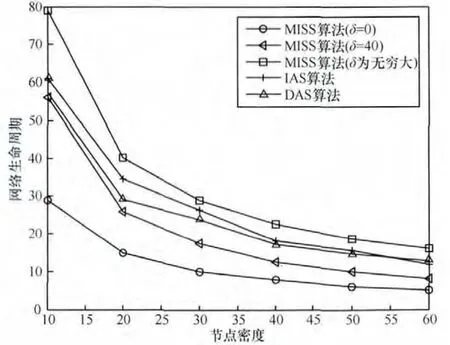
图10 节点具有不同权重时网络生命周期随节点密度变化比较

从前面的实验结果中可以看出阈值δ对MISS算法的性能影响非常明显，为了进一步研究和分析算法对δ取值的敏感性，在第3组实验中对节点数量N等于200、400和1 000这3种情况下，算法性能随δ的变化情况进行了仿真比较。

图11为3种不同节点数量下MISS算法融合时延随阈值δ的变化曲线，δ的取值从0增加至320。当δ从0变化至40时，3种节点数量下的融合时延降低的非常明显，如N=1 000时的融合时延从160左右降低至约100，减少了约40%。随着δ取值的不断增加，N=200的融合时延首先进入稳定阶段，δ从40增加到320时，其融合时延基本稳定在18左右。

第3组实验中平均加权时延的比较如图12所示。通过对比不同节点数量下加权时延的变化情况可以发现，δ的取值为某一个中间值时加权时延最优。从MISS调度算法的角度来分析，在选取每个时隙中的调度队列时，如果 δ=0，则表示选择所有链路的近似最大加权独立集，即该调度序列的权重最大，但可能链路数量相对较少，且其中必然有满足条件的中间链路，这2种情况都会导致整体传输时延的增大，并最终使得加权时延总和的增加，所以此时平均加权时延并非最优。另一个方面，如果δ足够大，则会限制中间链路的传输，增加边沿链路的并发数量，进而降低融合时延，但却无法保证加权公平性，即平均加权时延也不能得到优化。此时，需要找到最优的 δ，该数值能够很好地在加权公平性保证和融合时延之间实现平衡，并最终得到最小的平均加权时延，如N=1 000时，δ=80其加权时延最低。

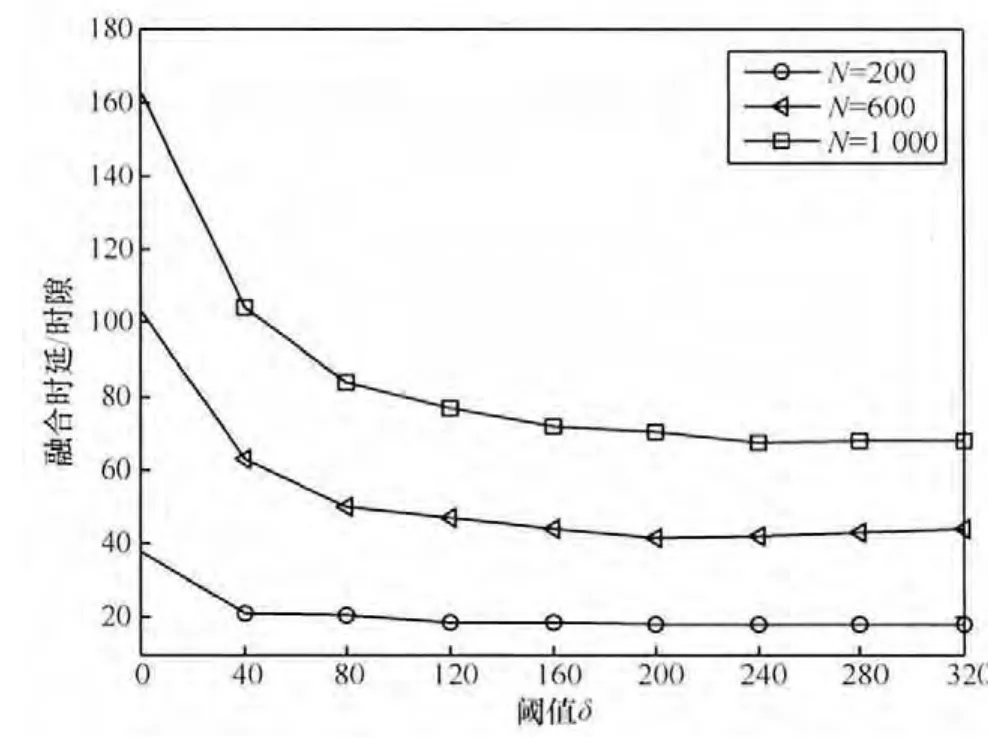
图11 不同节点数量下融合时延随阈值δ的变化比较

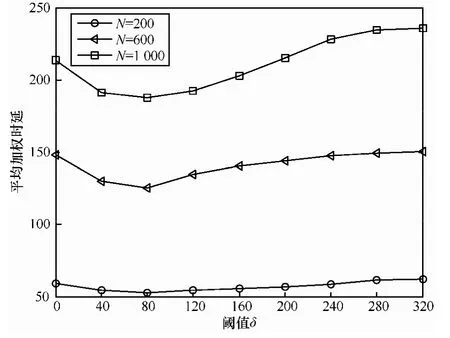
图12 不同节点数量下平均加权时延随阈值δ的变化比较

图13 为不同节点数量下网络生命周期随阈值δ的变化情况。MISS算法和其他算法相比，其最主要的特点之一是通过阈值来调节对节点通信次数的限制。不难理解的是当δ取值为0时，表示没有调度次数的限制，对于任意的中间链路，只要其权重满足一定条件均可以多次进行通信，此时网络的生命周期最小。随着δ的增加，限制也越来越严格，只有当中间节点接收到一定数量的数据，其累计权重达到限定条件时才会被纳入到激活链路集合中，作为可以被调度的对象。当δ增大到一定的程度时，中间链路成为激活链路的几率将保持在稳定状态，网络的生命周期也随之稳定。从实验结果可以看出，当δ≥120时，3种节点数量下的网络生命周期都基本保持不变。

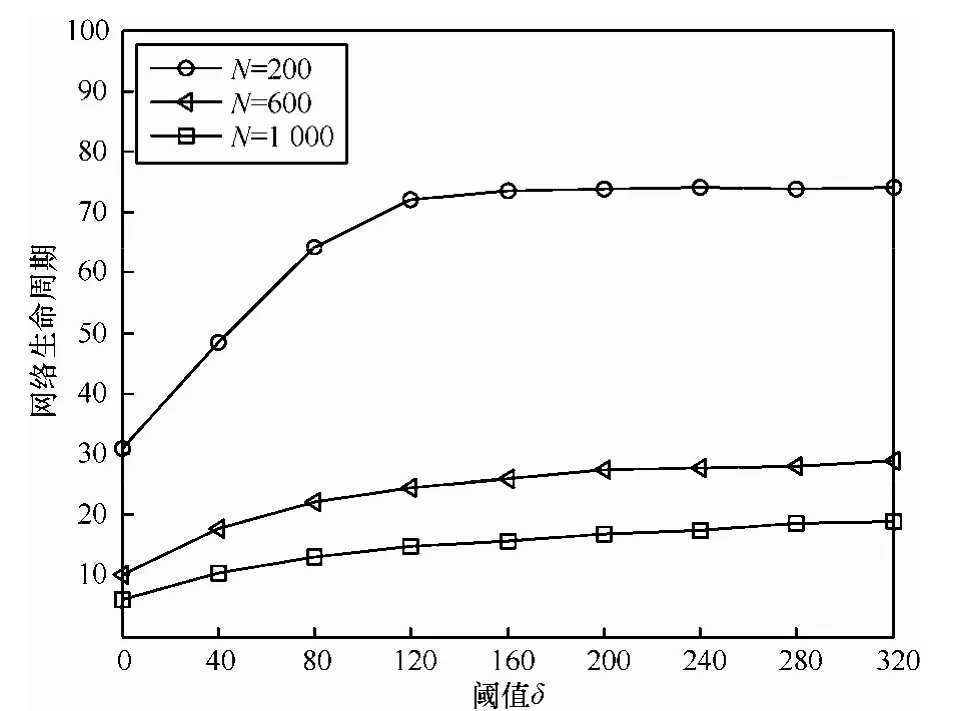
图13 不同节点数量下网络生命周期随阈值δ的变化比较

6 结束语

本文针对无线传感器网络中的数据融合调度问题，提出了一种基于二次独立集的调度算法。该调度算法分为2个阶段，第一阶段中通过选取最大独立集然后构成以最小连通支配集为骨干的数据融合树；第二阶段中则通过阈值δ优化允许进行调度的链路集合，即激活链路集，并将某一时刻融合树中激活链路集的近似最大加权独立集作为该时隙内的调度队列。实验结果分析表明，一方面该算法通过调度最大加权独立集以降低加权时延，保证加权公平性；另一方面通过引入阈值δ调节链路的发送次数限制，有效地实现了加权公平性与融合时延、网络生命周期三者之间的性能平衡。

在下一步工作中，笔者将重点研究如何在各种不同类型的数据融合下设计高性能调度算法，而不仅仅局限于本文中设定的完全融合。另外，算法在控制开销和数据传送成功率等方面的性能也将是一个需要深入研究的方向。

[1] ERGEN S C, VARAIYA P. TDMA scheduling algorithms for wireless sensor networks[J]. Wireless Networks, 2010, (16):985-997.

[2] ERGEN S C, VARAIYA P. PEDAMACS: Power efficient and delay aware medium access protocol for sensor networks[J]. IEEE Transactions on Mobile Computing, 2007, 5(7):920-930.

[3] FASOLO E, ROSSI M, WIDMER J, et al. In-network aggregation techniques for wireless sensor networks: a survey[J]. IEEE Transactions on Wireless communication, 2007, 14(2):70-87.

[4] LUO D J, ZHU X J, WU X B. Maximizing lifetime for the shortest path aggregation tree in wireless sensor networks[A]. Proceedings of the IEEE INFOCOM[C]. Shanghai, China, 2011.1566-1574.

[5] GHOSH A, INCEL O D, ANILKUMAR V S. Multi-channel scheduling and spanning trees: throughput-delay tradeoff for fast data collection in sensor networks[J]. IEEE/ACM Transactions on Networking, 2011, 19(6): 1731-1744.

[6] HUANG S C, WAN P J, VU C T, et al. Nearly constant approximation for data aggregation scheduling in wireless sensor networks[A].Proceedings of the IEEE INFOCOM[C]. Alaska, USA, 2007.366-372.

[7] YU B, LI J Z, LI Y S. Distributed data aggregation scheduling in wireless sensor networks[A]. Proceedings of the IEEE INFOCOM[C].Rio, Brazil, 2009.2159-2167.

[8] XU X H, LI X Y, MAO X F. A delay-efficient algorithm for data aggregation in multi-hop wireless sensor networks[J]. IEEE Transactions on Parallel and Distributed Systems, 2011, 22(1):163-175.

[9] JOO C H, CHOI J G, SHROFF N B. Delay performance of scheduling with data aggregation in wireless sensor networks[A]. Proceedings of the IEEE INFOCOM[C]. San Diego, USA, 2010.1-10.

[10] GUPTA P, KUMAR P R. The capacity of wireless networks[J]. IEEE Transactions on Information Theory, 2000, 46(2):388-404.

[11] BALJEET M, IOANIS N, MARIO A N. Aggregation convergecast scheduling in wireless sensor networks[J]. Wireless Networks, 2011,17:319-335.

[12] WU Y W, LI X Y, LIU Y H, et al. Energy-efficient wake-up scheduling for data collection and aggregation[J]. IEEE Transactions on Parallel and Distributed Systems, 2010, 21(2):275-287.

[13] WU Y, FAHMY S, SHROFF N B. On the construction of a maximum lifetime data gathering tree in sensor networks: np-completeness and approximation algorithm[A]. Proceedings of the IEEE INFOCOM[C].Phoenix, USA, 2008.1013-1021.

[14] HAN B, FU H H, LIN L D, et al．Efficient construction of connected dominating set in wireless ad hoc networks[A]. Proceedings of the IEEE International Conference on Mobile Ad-hoc and Sensor System[C]. Florida, USA, 2004.570-572．

[15] CHALERMEK I, RAMESH G, DEBORAH E. Directed diffusion: a scalable and robust communication paradigm for sensor networks[A].Proceedings of the Sixth Annual International Conference on Mobile Computing and Networking (MobiCOM '00)[C]. Boston, USA, 2000.