基于系统动力学的网络安全攻防演化博弈模型

朱建明，宋彪,2，黄启发

(1. 中央财经大学 信息学院，北京 100081；2. 内蒙古财经大学 会计学院，内蒙古 呼和浩特 010051)

1 引言

近年来，网络安全问题日益突出，网络安全技术成为研究的热点。但是在网络安全技术的研究方面，通常着重从技术上对某项或某几项指标进行完善，却忽略了客观存在的非合作系统行为。事实上网络安全的策略研究在某种程度上比技术研究更为重要，特别是对于同样的技术采用不同的安全策略会取得不同的效果。网络安全中攻防对抗的本质可以抽象为攻防双方的策略依存性，而这种策略依存性正是博弈论的基本特征，因而可以考虑应用博弈论来解决网络安全攻防对抗的问题[1]，博弈论应用于网络安全是未来重要的一个研究方向[2]。目前网络攻防的博弈分析尚处于发展阶段，国外学者Stakhanova等人，通过随机博弈、不完全信息博弈等模型来进行入侵意图、目标和策略的推理[3]。Reddy指出关于入侵检测的研究主要且多数建立在一次性博弈分析的基础上[4]，SHEN Shi-gen认为考虑到真实场景中攻击的重复性，将其视为一个重复的多阶段博弈[5]的过程显然更为合理。Agaha等建立了无线传感器网络中基于重复博弈理论的攻防模型[6]，效果比较理想。国内也有学者应用博弈论研究网络安全。朱建明提出了基于博弈论对信息安全技术进行评价的模型[7]，其研究侧重于信息安全机制的优化配置。张勇提出了一种基于Markov博弈分析的网络安全态势感知方法[8]，但网络的节点和路径较多时，很难做到实时评估。孙薇等人建立了信息安全攻防的博弈模型，分析防守方和攻击方的复制动态及进化稳定策略[9]，其模型考虑到现实社会中的有限理性，引入了演化博弈来研究攻防对抗的规律，但该研究把攻防双方的技术学习与社会网络分离，旨在降低防守方的成本同时，单方增加攻击方的攻击成本，这种理想化的假设，在两方博弈演化过程中，缺乏现实可行性。姜伟等人提出了基于主动防御的博弈分析方法，但该方法无法描述不同攻击能力下攻击者策略集和效用的差异性。同时防御图模型及其相应的策略分析方法不能适应对复杂网络的建模和分析[10]，在实践中主动防御的病毒识别时间和效率，比过去的特征码更慢。该方法对新的入侵行为的确定分析，也需要一定的时间，需要用户有足够的计算机知识和耐心，误杀可能会偏高一些。另外主动防御有加重企业负担，偏离经营主旨之嫌。总之，上述基于博弈论的网络安全研究，多着眼于微观技术改进角度解决信息安全问题，而从宏观管理角度对信息安全问题进行深入探讨较少。

2 攻防演化博弈模型

在信息网络中，由于不同的攻击者和防御者对信息安全知识的不同理解和反应，因此产生了不同的预测和决策机制。每个参与者获得不同的收益，随着时间的推移，每个参与者通过学习成功者的经验，不断改进自己的安全策略，形成新的攻防形势。在参与者不断改进攻防策略的内在驱使下，随着网络安全技术不断进步，企业对系统的持续调整，都会使信息安全问题呈动态进化趋势[11]，进而形成了不断进化的网络安全体系。

通常将网络攻防的主体定义为攻击者和防守者，但是在实际应用中，攻击者和防守者的界限有时是模糊的。攻击者在一定环境下，可以转化为防守者，而防守者有时也会做出攻击行为，因此，防守方和攻击者的安全技术在群体环境下，没有绝对差异。

定义1 设防守收益为P1，攻击收益为P2，防守收益P1为防守方信息资产的价值，包括信息资产自身的价值和信息资产对企业造成的其他影响价值；攻击收益P2为攻击方获得信息资产的价值，和攻击行为带来的其他影响价值。为简化攻防问题，可以假设 P1=P2，这里的收益是从损失的角度来计量的。

定义2 设防守成本为C1，表示防守方投入设备、人力和无形资产等全部的价值。

定义3 设攻击成本为C2，表示攻击方在人力、设备和法律惩罚等方面产生的投入。

定义 4 纳什均衡是所有参与者的最优战略的组合。

构建的博弈树如图1所示。

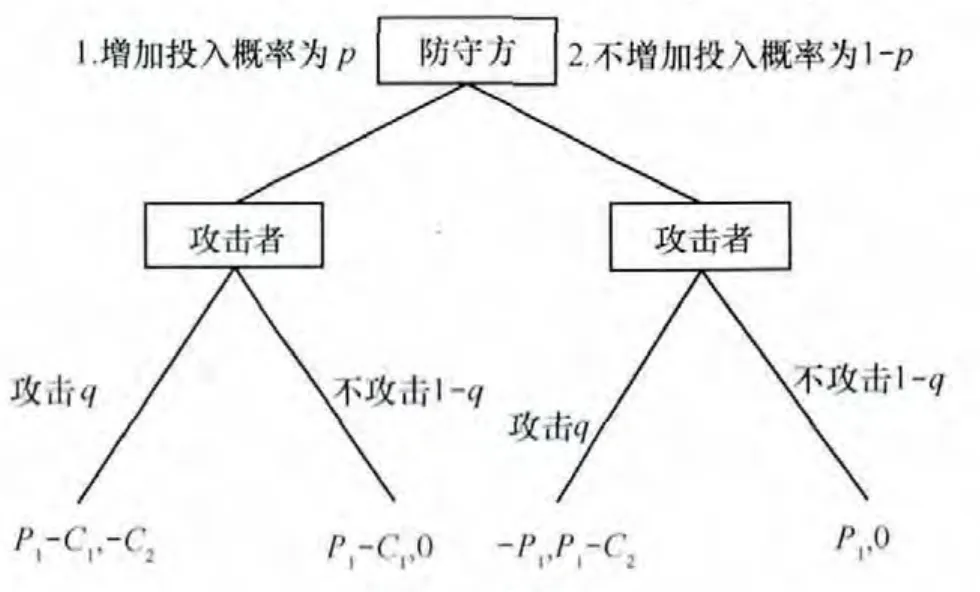
图1 攻防博弈树

在上述假设条件下，计算防守者的期望收益和平均收益

当投入效益和不投入效益不相等时，效益差的防守者会模仿效益好的防守者，则采取投入策略与采取不投入策略人的比例是时间的函数，分别表示为 p(t)和 1-p(t)。

投入策略的动态变化速度可以用如下复制动态方程表示

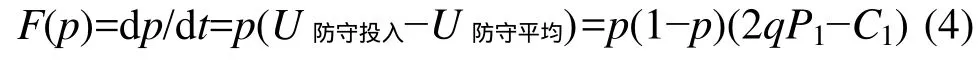
同理，计算攻击者的情况：

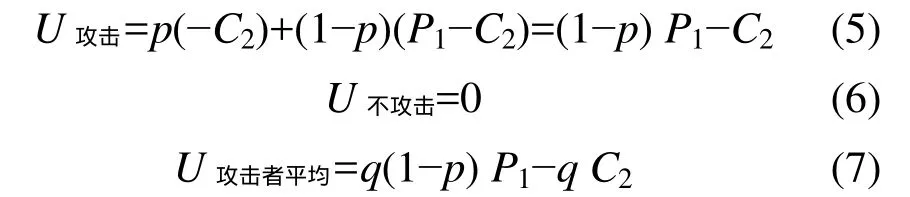
平衡状态，得到：

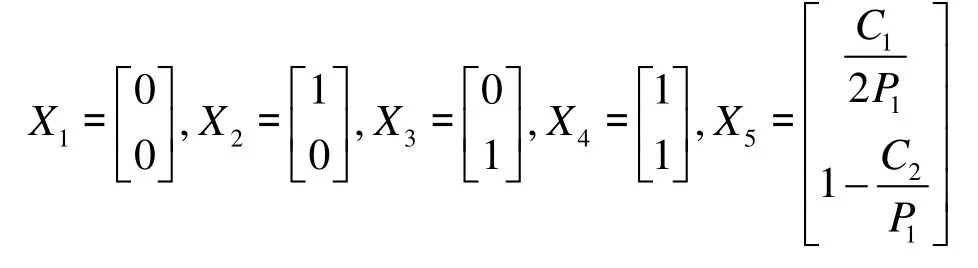
其中，X1、X2、X3、X4为鞍点，X5为中心点，系统不存在演化稳定均衡，只要有微小的变化，系统就会受到重大的影响。这说明网络安全问题仅靠技术的投入是无法得到解决的。

3 系统动力学模型构建及仿真分析

用系统动力学对相关问题的演化博弈进行仿真，可以从全局整体考察博弈均衡背后的动态特性，而演化博弈论的分析则对建模和制定相应的决策起到了至关重要的作用[12]。

3.1 模型的基本假设

3.1.1 系统边界的定义

清晰的界定系统的边界是模型成功与否的关键步骤。界定系统的边界必须紧紧围绕建模目的以及研究对象，真正将关注点放在核心问题上，可以考虑忽略非重要的因素[13]。研究的对象是网络中攻防双方的演化博弈系统。从参与者结构来看，系统内存在两类个体：防守方和攻击方。从演化的范围来看，系统演化包括防守方之间的学习、攻击方之间的学习以及防守方和攻击方之间的对抗。从影响因素来看，根据演化博弈模型的分析框架，系统影响因素应包括防守方收益、防守方成本、攻击方收益和攻击方成本。网络中攻防演化博弈系统的构成要素如表1所示。

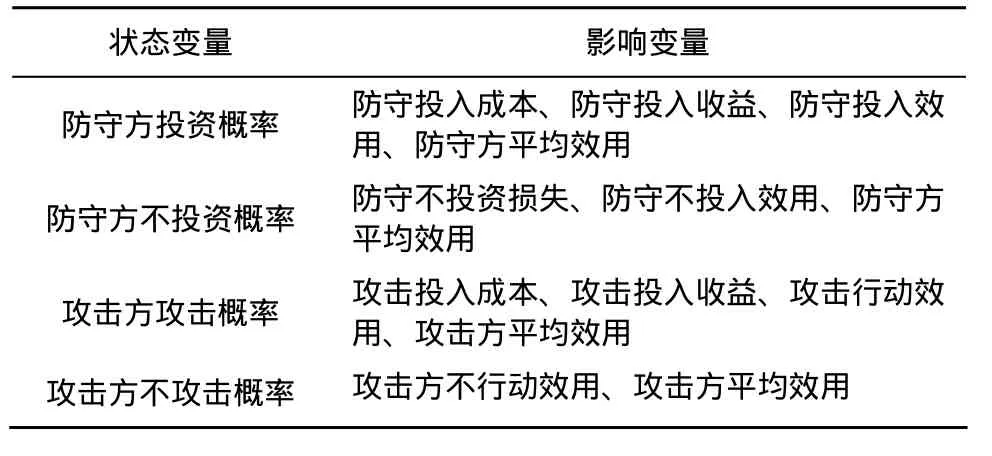
表1 系统构成要素

3.1.2 基本假设

模型的基本假设如下。

1) 攻防双方演化博弈系统限定在网络上的攻防双方，在根据对方的策略集采取策略演化。不考虑攻防角色的转化以及蜜罐技术等其他因素。

2) 一般假设攻击方和防守方对信息资产的价值认可是相同的。

3) 在足够长的时间内，攻击者的技术水平和防守方的技术水平没有绝对差距。

4) 攻击方和防守方通过社会网络，能够各自充分了解同质群体采取行动的效用。

5) 防守方采取的行动是完全有效的。

3.2 模型构建

网络安全演化博弈系统动力学模型由 4个流位、2个流率、13个中间变量和3个外部变量构成，如图2所示。其中，流率变量和中间变量主要由演化博弈中的动态复制方程的逻辑关系进行定义，流位变量和外部变量如表2和表3所示。

表2 流位变量说明

3.3 模型检验

系统动力学模型是对真实世界系统抽象和简化的结果，并不是真实世界系统的复制品，所以从再现客观世界真实情况来看，任何模型都不是完全正确的[14]。只要模型在既定的假设下有效接近真实世界的系统，完成既定条件下的目标，那么就可以认为模型的构建具有客观性、合理性和实用性。

3.3.1 系统边界检验

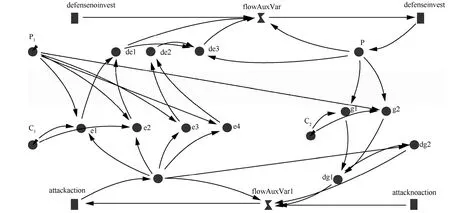
图2 攻防博弈系统动力

系统边界测试主要是检查系统中重要的概念和变量是否为内生变量，同时测试系统的行为对系统边界假设的变动是否敏感[9]。用系统动力学对演化博弈建模的目的，是研究网络攻防演化过程中系统内部影响因素的动态特征，并通过这些影响因素找出网络攻防的优化策略集。模型的边界是在继承前期网络攻防博弈的相关研究成果基础上[15]，根据建模目的和现实系统的实际情况而确定的。该模型包含了与所研究问题密切相关的重要因素，并摒除了对系统影响较小的因素，因此对网络攻防演化博弈的系统边界是合理、有效的。

3.3.2 有效性检验

模型在使用前要进行有效性检验，有效性检验是为了验证模型所获信息与行为是否反映了实际系统的特征与变化规律，通过模型的分析研究能否正确认识与理解所要解决的问题[16]。在现实的网络环境中，攻防双方都根据对方的行动采取相应的策略。

如果初始状态为防守方都进行有效安全投资，攻击方都进行攻击，那么经过一段时间演化，攻防对抗不断升级，这种状态是攻守双方处于不良循环的状态，系统仿真中假设攻防双方初始状态为1时，经过演化，攻防双方采取行动概率保持为1，如图3和图4所示。

如果初始状态为防守方都进行有效安全投资，攻击方没有收益，那么经过一段时间演化，攻击方攻击概率都将降为 0，仿真中假设攻击方初始状态为0.9时，经过演化，攻击方进行攻击概率迅速降至0，如图5和图6所示。

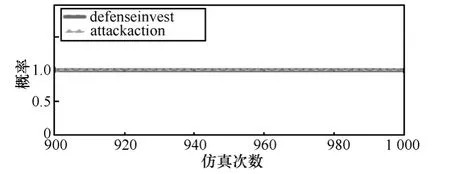
图3 攻防概率变化对比

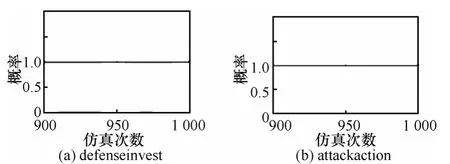
图4 攻防概率变化

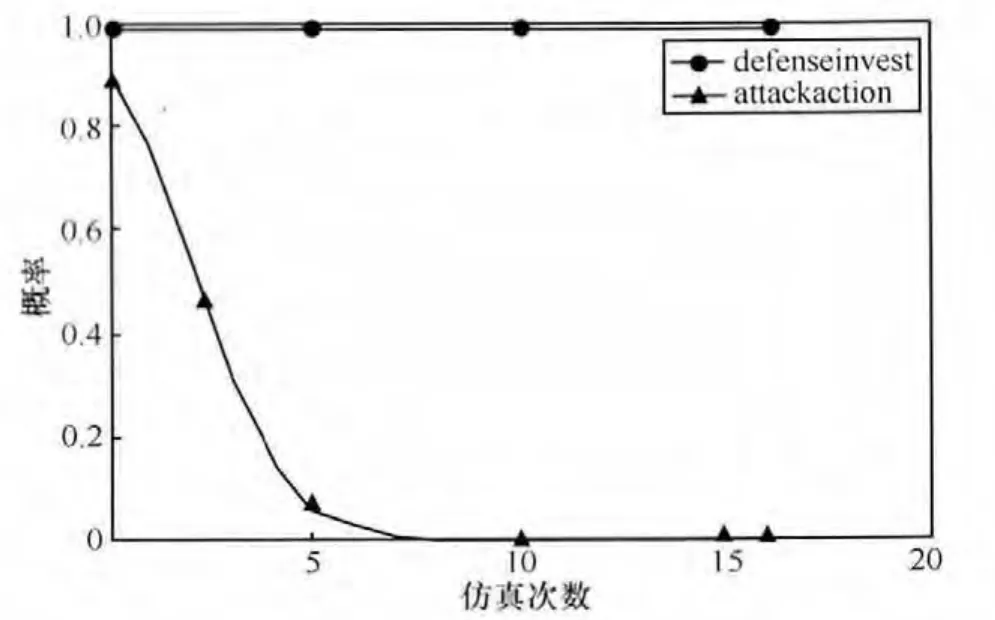
图5 初始防守概率为1，攻击概率0.9概率变化对比

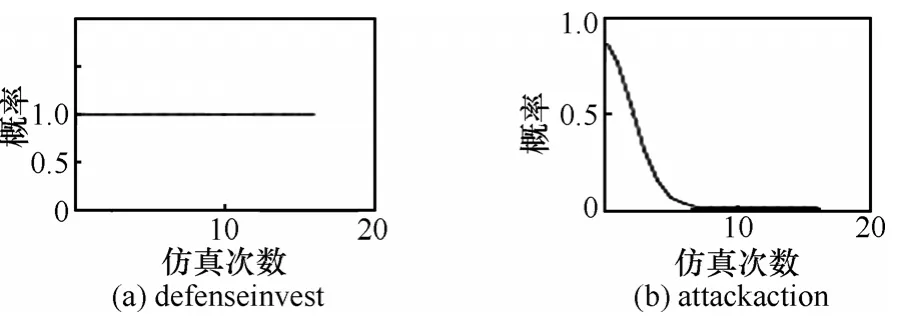
图6 初始防守概率为1，攻击概率为0.9时概率变化

如果初始状态为攻击方都采取攻击行动，防守方受到损失，经过一段时间演化，防守方都将进行安全投资。系统仿真中假设所有攻击方都进行攻击，防守方初始状态为0.1时，经过演化迅速达到1的均衡状态，如图7和图8所示。

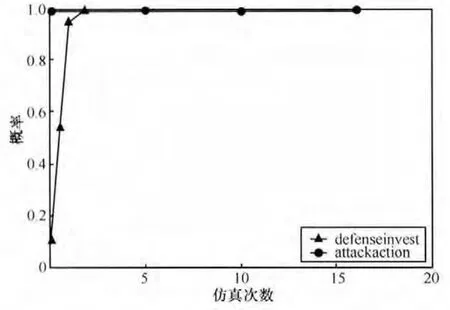
图7 初始攻击概率为1，防守概率为0.1时概率变化对比

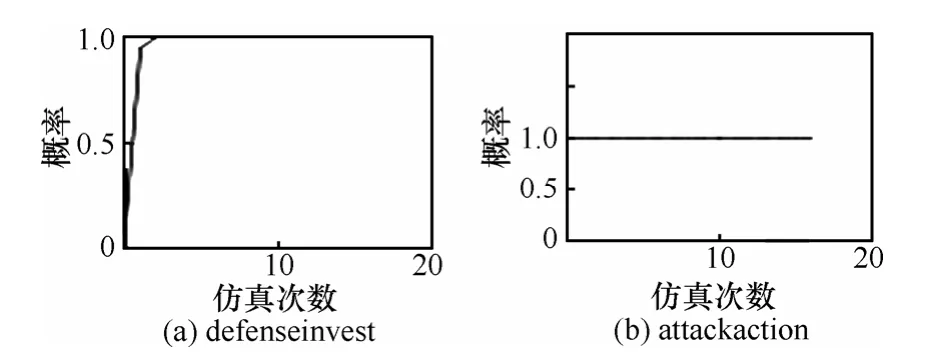
图8 初始攻击概率为1，防守概率为0.1时概率变化

综上所述，通过观察对比，不难发现这些变量的模拟结果，与现实系统中的变化规律基本一致，因此，对网络攻防演化博弈系统的建模是有效的。

3.3.3 参数灵敏度检验

参数灵敏度检验是用于研究参数的变化对系统行为的影响程度。如果模型中参数方程或模拟方程改变后所得到的模型行为曲线有较大变化，那么模型的参数是灵敏的，反之是不灵敏的[17]。经过反复模拟，可以确定攻防参与者概率参数是模型的敏感性因素，因此选择攻防参与概率来测试模型的灵敏度。将p由原来的0.9（曲线1）调整为0.95（曲线2），模拟结果如图9所示。模型的行为变化趋势没有出现变动，说明模型参数是不灵敏的。由此，模型对参数的要求不苛刻，模型有较强的实际应用意义。

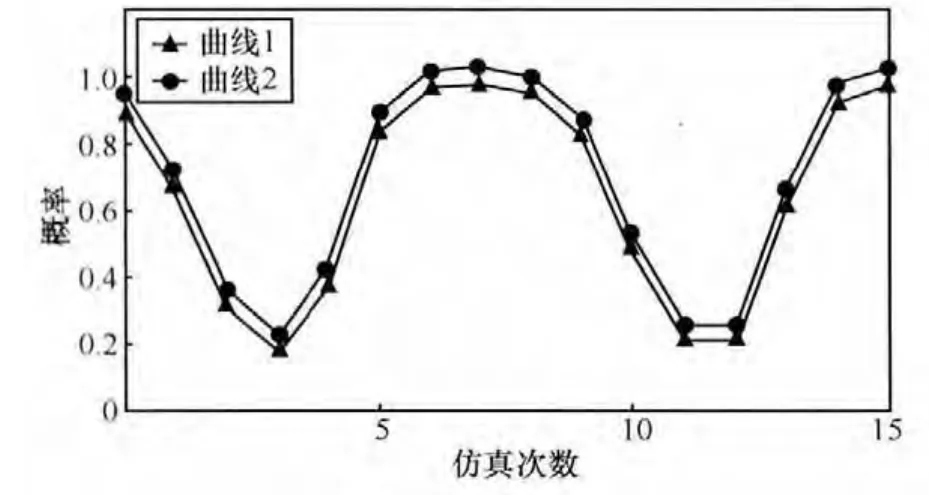
图9 灵敏度检验

总之，经过模型检验，可以认为模型基本反映了信息安全攻防的规律，具有一定的客观性、科学性和应用价值。

4 模型仿真与结果分析

利用建立起来的模型，通过改变相关参数，运行和分析在不同情况下的仿真结果，得到一些对于分析网络攻防策略的有益启示。

考虑现实意义，令P1=3，C1=1，C2=1（可以为其他值）仿真1 000步，研究防守方和攻击方在不同初始值条件下的演化博弈系统的动态特性。

假设初始值当所有防守方都采取行动时，所有攻击方都选择攻击，博弈双方的都为均衡状态，博弈双方没有一方主动改变自身的策略，初始值当所有攻击方选择攻击，防守方都采取防守行动时，博弈双方也不会有一方改变自身的策略，如图3和图4所示。

假设初始值所有防守方都采取行动，而攻击方只有部分选择攻击，攻击方会改变自身策略，最后达到所有攻击者都选择放弃行动的策略，如图5和图6所示。

假设初始值所有攻击者都采取行动，而防守方只有部分选择防守策略时，防守方会改变自身的策略，最后达到所有防守者都选择采取防守投资的策略，如图7和图8所示。

假设攻防双方初始都没有在均衡状态，防守方采取投资概率0.9，攻击方采取行动概率0.1（可以为其他值，只需不在均衡点0和1）。

仿真结果显示，双方随机选择防守和攻击的概率为初始值时，只要初始值与混合策略的纳什均衡值存在差异，博弈双方的策略选择就会存在波动，随着博弈次数和时间的增加，波动振幅逐渐增大，甚至达到最大振幅，博弈过程变得难以把握，如图10~图12所示。

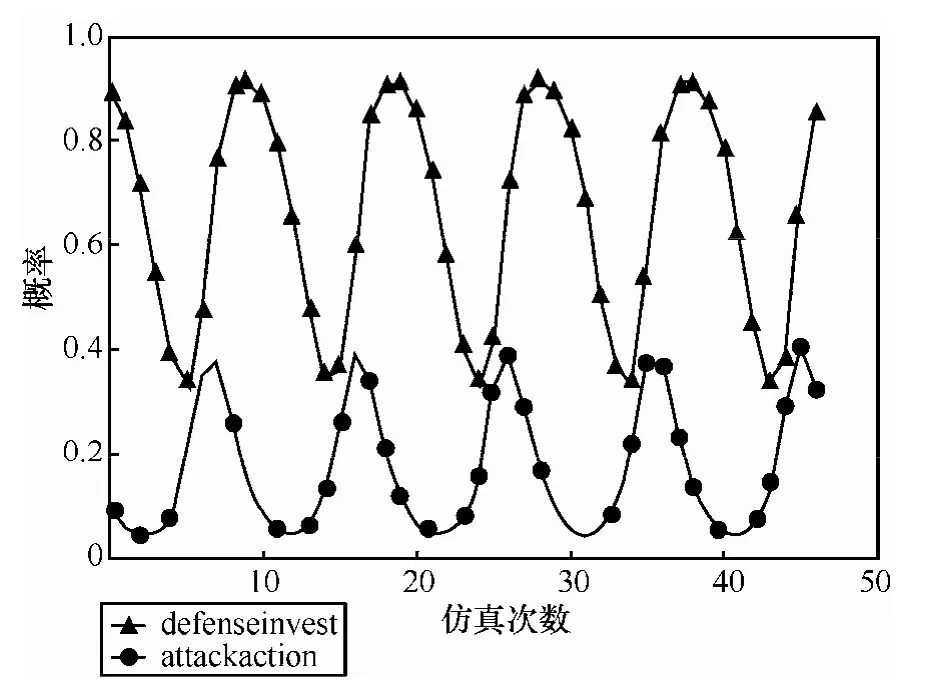
图10 双方博弈演化过程（防0.9、攻0.1）

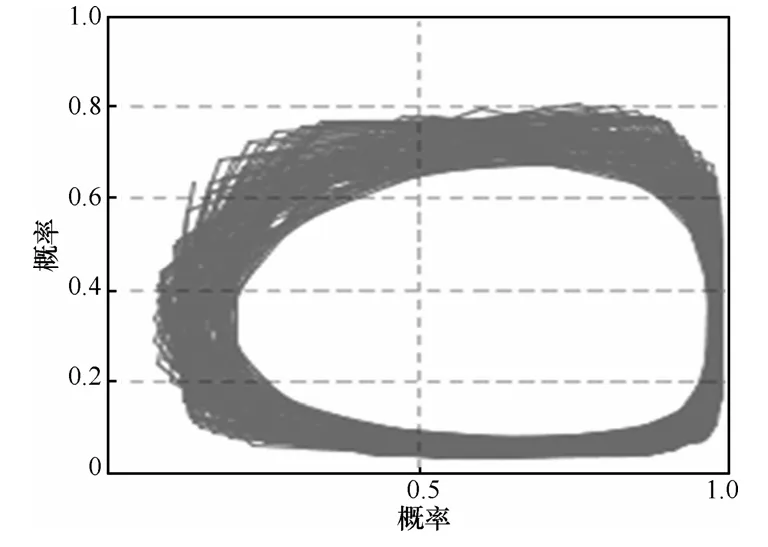
图11 双方博弈均衡点变化（防0.9、攻0.1）

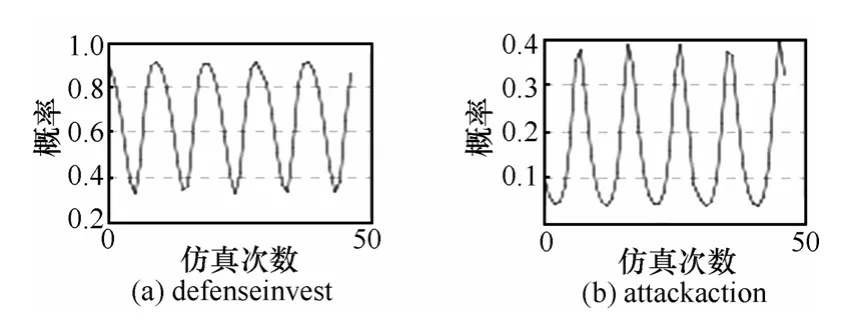
图12 防守和攻击方采取行动概率变化

研究信息攻防博弈的学者最常见的治理策略就是提高攻击者的成本，或加大对攻击者的惩罚力度。针对类似问题，有学者已经证明混合战略博弈中提高惩罚力度，其实无法改变被惩罚者违规概率的均衡点。实践中加大惩罚力度策略得以广泛应用，是因为其在短期内可以降低被惩罚者的均衡点[18]，而从长期来看，该策略忽视了惩罚力度的加大实际上对于博弈双方的支付矩阵都是有影响的。

一般来说防守者投资概率越高，攻击者采取行动的成本越高，或者被发现的概率越大，导致受到惩罚的可能越大，系统仿真中设C2=2+p×2时（可以为其他形式），在短期内，攻击者的攻击概率可以下降至 0，但从长期来看，由于防守方策略也受影响，攻击者的概率不会稳定在较低点，而是波动起伏的，如图13和图14所示，而且随着博弈次数和时间的变化，波动振幅也会加大，博弈无法达到演化均衡点，如图15所示。

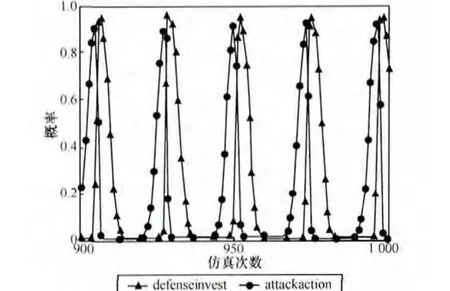
图13 双方演化博弈过程（C2=2+2p）

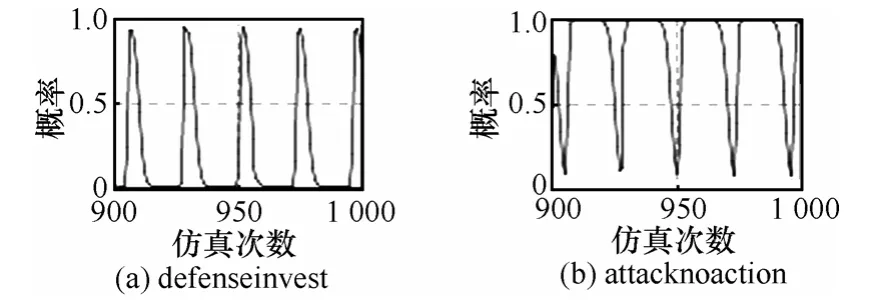
图14 防守方和攻击方概率变化（C2=2+2p）

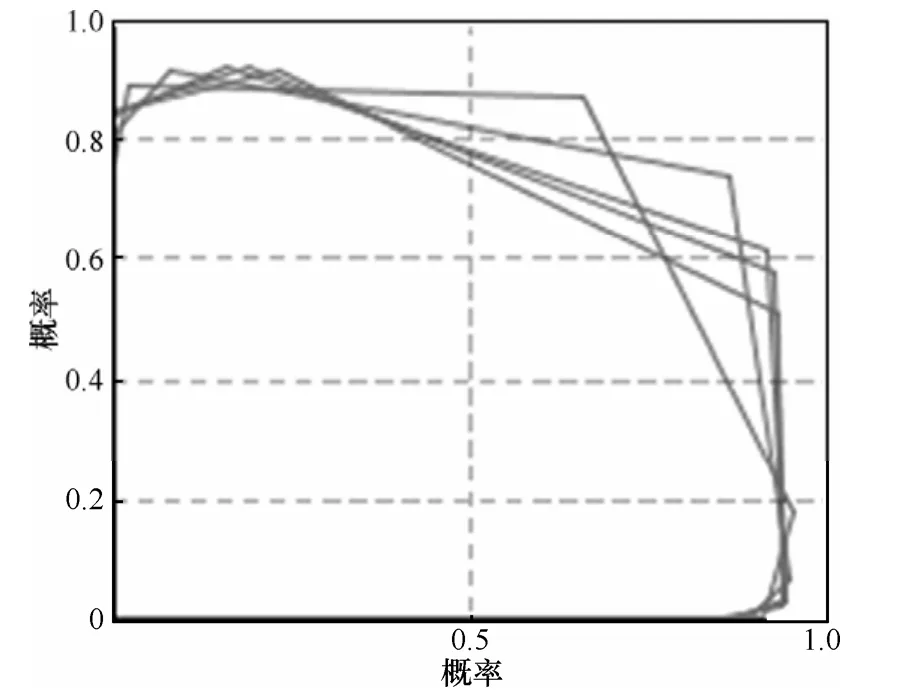
图15 双方博弈均衡点变化（C2=2+2p）

所以，依靠防守方加大投资，是无法达到演化均衡的，最终呈现攻防双方反复波动的状态。

当加入动态惩罚策略，如果第三方监管部门对攻击者的惩罚力度，是随着攻击者采取攻击的概率大小而变化的，考虑对整个博弈模型的稳定性影响。系统中假设当 C2=2+2q（可以为其他形式）时，随着博弈次数和时间的增加，攻击者采取攻击的概率逐渐收敛，稳定在纳什均衡点。如图16~图18所示。

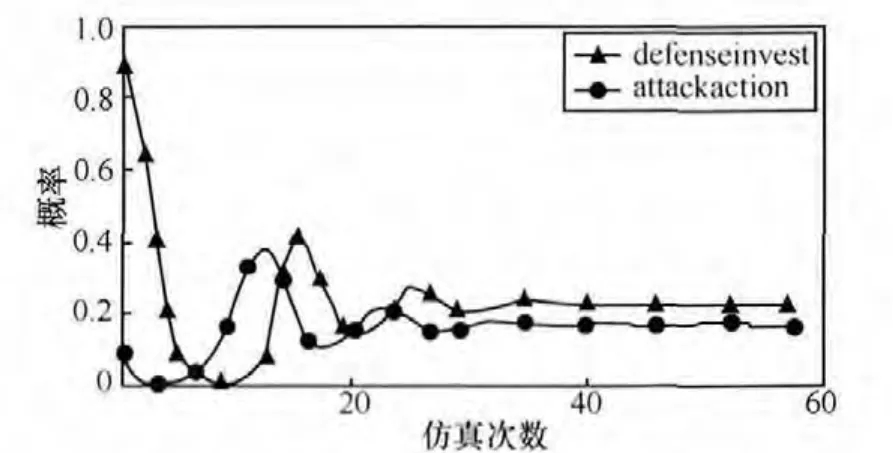
图16 双方演化博弈过程（C2=2+2q）

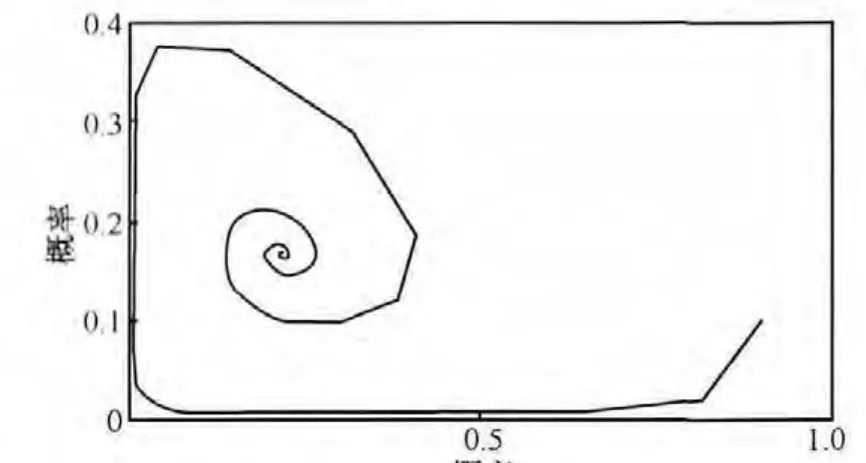
图17 双方博弈均衡点变化（C2=2+2q）

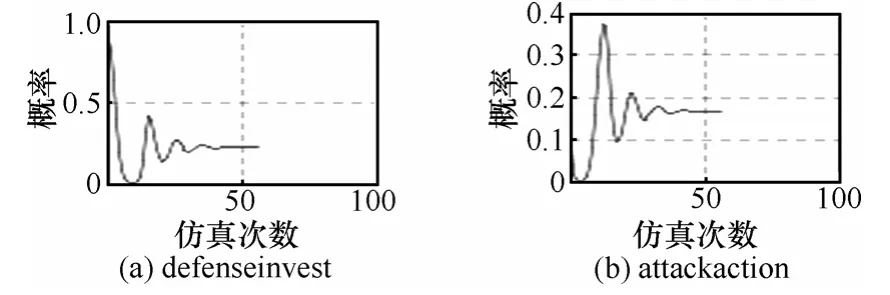
图18 防守方和攻击方概率变化（C2=2+2q）

可以发现，引入第三方动态惩罚策略的系统博弈是存在演化均衡的。现实中，防守方投资如果侧重于攻击者攻击的追踪，为第三方监管部门进行动态惩罚提供网络攻击行为的审查线索，是有效遏制网络攻击的重要途径。

5 结束语

用系统动力学和演化博弈对信息安全攻防建模，经过检验，模型符合现实中网络安全攻防的规律。通过仿真分析发现，模型能够直观解释网络安全治理中攻防不断升级的原因，这表明模型具有客观科学性。最终根据模型指出，网络安全问题的治理是综合了多个学科知识的复杂问题。一直以来，博弈论就被应用于计算机网络领域，很多文献利用博弈论解决网络资源分配问题[19]，相关应用和研究比较广泛和深入。然而多数利用博弈论在网络安全领域的研究，仅从安全技术角度出发，无法彻底解决攻防双方投入不断升级的困境。根据系统动力学方法，对网络安全攻防演化模型所构建的系统进行微调和观察，发现通过第三方监管部门，采取对攻击者收益的动态惩罚策略，对改善攻防双方的恶化情形有重要影响。实践中涉及到数据安全的法律以及网络监管角度，需要一种机制能够远程、公开地对数据进行审计[20]。因此，在发展信息安全技术方面，为第三方监管部门追踪网络攻击者，以及提供相关审查线索的相关研究，有必要更加重视发展。

[1] ANDERSON R. Why information security is hard —an economic perspective[A]. Proceedings of 17th Annual Computer Security Application Conference[C]. Washington, DC, USA: IEEE Computer Society, 2001.39-40.

[2] HAMILTON S N, MILLER W L, OTT A, et al. The role of game theory in information warfare[A]. 4th Information Survivability Workshop[C]. Vancouver, Canada, Washington, DC, USA: IEEE Computer Society Press, 2002.45- 46.

[3] BASUS S,WONG J. A taxonomy of intrusion response systems[J].International Journal of Information and Computer Security, 2007,1(1/2):169-184.

[4] REDDY Y B. A game theory approach to detect malicious nodes in wireless sensor networks[A]. Procof the 3rd International Conference on Sensor Technologies and Application[C]. Washington, DC, IEEE Computer Society, 2009.462-468.

[5] SHEN S G, LI Y J, XU H Y. Signaling game based strategy of intrusion detection in wireless sensor networks[J]. Computers &Mathematics with Applications,2011,62(6):2404-2416.

[6] DADSK A. Preventing DoS attacks in wireless sensor net works: a repeated game theory approach[J].International Journal of Network Security, 2007,5(2):145-153.

[7] 朱建明. 基于博弈论的信息安全技术评价模型[J]. 计算机学报,2009,(4): 828-834.ZHU J M. Evaluation model of information security technologies based on game theoretic[J]. Chinese Journal of Computers, 2009, (4):828-834.

[8] 张勇.基于Markov博弈模型的网络安全态势感知方法[J].软件学报,2011,22(3):495-508.ZHANG Y. Network security situation awareness approach based on markov game model[J]. Journal of Softwar, 2011,22(3):495-508.

[9] 孙薇.基于演化博弈论的信息安全攻防问题研究[J]. 情报科学,2008, (9): 1408-1412.SUN W. Research on attack and deference in information security based on evolutionary game[J]. Information Science, 2008, (9), 1408-1412.

[10] 姜伟.基于攻防博弈模型的网络安全测评和最优主动防御[J].计算机学报, 2009,(4):817-827.JIANG W. Evaluating network security and optimal active defense based on attack-defense game model[J].Chinese Journal of Computers,2009(4), 817-827.

[11] 宋彪, 朱建明. 基于业务流程的ERP信息安全进化熵的风险评估[J].通信学报, 2012, 33(9):210-215.SONG B, ZHU J M. Evolution entropy risk assessment of ERP information security based on the business process[J]. Journal of Communication, 2012, 33(9):210-215.

[12] 蔡玲如.基于系统动力学的环境污染演化博弈问题研究[J].计算机科学, 2009(8): 234 -257.CAI L R. System dynamics model for a mixed-strategy game of environmental pollution[J].Computer Science, 2009, (8), 234-257.

[13] 钟远光, 贾晓菁, 李旭等. 系统动力学[M].北京:科学出版社,2009.ZHONG Y G, JIA X J, LI X, et al. System Dynamics[M]. Beijing:Science Press, 2009.

[14] STERMAN J D. Business Dynamics: Systems Thinking and Modeling for A Complex Word[M].New York:McGraw-Hill,2000.

[15] 林旺群.基于非合作动态博弈的网络安全主动防御技术研究[J]. 计算机研究与发展, 2011,48(2):306-3l6.LIN W Q. Research on active defense technology in network security based on non-cooperative dynamic game theory[J].Journal of Computer Research and Development, 2011,48(2):306-3l6.

[16] 杨刚, 薛惠锋. 高校团队内知识转移的系统动力学建模与仿真[J].科学与科学技术管理, 2009,(6):87-92.YANG G. XUE H F. Modeling and simulation of knowledge transfer in groups of universities using system dynamics[J].Science of Science and Management of S & T, 2009, (6):87-92.

[17] 吴传荣, 曾德明, 陈英武.高技术企业技术创新网络的系统动力学建模与仿真[J]. 系统工程理论与实践,2010(4):587-593.WU C R ZENG D M, CHEN Y W. Modeling and simulation of high-tech enterprises innovation networks using system dynamics[J].Systems engineering-theory & practice, 2010(4):587-593.[18] DONG-HWAN K, DOAHOON K. A system dynamics model for a mixed-strategy game between police and driver[J]. System Dynamics Review, 1997,(13):33-52.

[19] 姜永,陈山枝,胡博.异构无线网络中基于 Stackelberg博弈的分布式定价和资源分配算法[J]. 通信学报, 2013, 34(1):61-67.JIANG Y, CHEN S Z, HV B. Stackelberg games-based distributed algorithm of pricing and resource allocation in heterogeneous wirelessnetworks[J]. Journal of Communication, 2013, 34(1):61-67.

[20] 杨健.云计算安全问题研究综述[J].小型微型计算机系统,2012,(3):473-479.YANG J. Survey on some security issues of cloud computing[J].Journal of Chinese Computer Systems,2012,(3):473-479.