异步电机矢量控制系统模糊PI控制器设计

郭 燚，张晓旭，李 硕

（上海海事大学物流工程学院，上海 201306）

0 引言

随着电动机的应用越来越广泛，异步电机的控制成为一个非常有意义的研究课题。目前，感应电动机调速一般采用变频调速系统，而脉宽调制(PWM)变频器是变频调速系统的一个重要组成部分［1－2］。在PWM技术中，SVPWM相比于SPWM方式，具有谐波抑制效果好、响应快速、电压利用率高、电流波形畸变小、转矩脉动低等优点，已经在电机驱动方面得到了广泛应用。

异步电机数学模型较为复杂，精确的数学模型难以建立，且时间常数较大。传统的PID调整有超调，响应有延迟，性能指标也不能令人满意。模糊控制作为一种智能控制方法，无需知道控制对象准确的数学模型，而按照人类的知识、经验去构造控制规则。用模糊逻辑控制器来代替电机矢量控制中的PI转速调节器，选择8个基本的电压矢量，可得到更优化的开关表，以实现对转矩和转速的实时控制，从而改善异步电机矢量控制系统的动态和稳态特性。

1 异步电机SVPWM控制策略

1.1 异步电机矢量控制

异步电机的矢量控制就是根据异步电机的坐标变换理论，在三相坐标系下，将定子输入的电流变换到两相旋转坐标系M，T轴中。并且使得M轴沿转子总磁链矢量的方向，最终获得等效成同步旋转坐标系下的直流电流ism、ist，从而可以把异步电机等效成输入电流为im1、it1的直流电机，进而获得与直流电动机一样良好的动态调速特性。矢量控制系统原理图如图1所示。

图1 异步电动机矢量变换和等效直流电动机模型

经过坐标变换，可得电压方程［3］:

电机转子磁链与电流关系:

将式(2)代入到式(1)第3行中，得到:

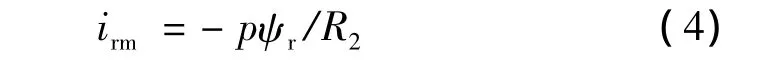
再代入式(2)，得:

式中，Tr为转子励磁时间常数，Tr=Lr/R2。T轴上的定子电流it1和转子电流it2的动态关系满足式(3)，或写成［3］:

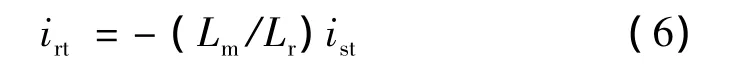
由式(1)和式(2)可得:

将式(6)代入式(7)，并考虑到Tr=Lr/R2，可得到转差频率控制方程式为:

2.4 患者临床症状体征 见表3。本研究中钩虫性十二指肠炎综合征患者临床表现多样，其中腹痛表现共76例，为主要常见临床表现。

电机的电磁转矩为:

式中:R1，R2为定转子电阻;Lm为定转子等效绕组间的互感，Lm=(3/2)Lsm。

从推导过程可知，将定子磁链分解为励磁分量ism和转矩分量ist，实现了对异步电动机中磁链和转矩的分别控制。从式(2)可以看出，磁链和励磁电流是一个具有一阶惯性的传递函数，这和直流电机的励磁特点十分类似。

1.2 电压空间矢量SVPWM技术

矢量控制系统为了实现对逆变器的控制，可采用多种脉宽调制技术，如SPWM和SVPWM。相较于传统电压SPWM来说，SVPWM将逆变电路和电机看做一个整体，模型简单且易于数字化实现。此外，该控制技术能明显减小电流波形畸变和电机谐波损耗，降低电机转矩脉动，提高直流电压利用率，被广泛应用于电机调速领域［4－8］。

SVPWM的理论基础是平均值等效原理，即在一个开关周期内通过对基本电压矢量进行合成，使其平均值与给定电压矢量相等［4］。图2所示为变频器输出电压空间矢量图。从图2可见，三相功率器件共有8个开关状态:S0=(0，0，0)，S1=(1，0，0)，S2=(1，1，0)，S3=(0，1，0)，S4=(0，1，1)，S5=(0，0，1)，S6=(1，0，1)，S7=(1，1，1)，同一相上下桥臂的开关状态互补。“1”表示相对应相上桥臂开关导通，“0”表示相对应的相下桥臂开关导通［9］。例如，“(1，0，0)”表示A相上桥臂开关导通，B、C两相下桥臂开关导通，而其余的开关都处于关断状态。

图2 电压空间基本矢量图

在每个开关周期内，开关状态的顺序为:S0(T0/4)→SA(T1/2)→SB(T2/2)→S7(T0/2)→SB(T2/2)→SA(T1/2)→S0(T0/4)，其中 SA和 SB为变频器参考电压矢量→ui所在扇区两侧的两个相邻开关状态。如果ux和uy分别是SA和SB所对应的电压矢量，ux和uy在每个开关周期内的各开关状态对应的工作时间T1、T2为［10－11］:

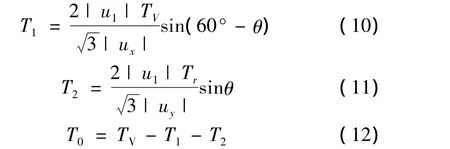
2 模糊PI控制器设计

在传统矢量控制系统中使用PI控制，其结构简单、稳定性好。但是由于异步电机数学模型复杂，参数和结构的不确定性，导致系统无法适应系统的参数变化和外部扰动。模糊控制则不依赖被控对象精确的数学模型，可改善电机的动态性能。

2.1 模糊控制原理

模糊逻辑控制由A.Zadeh于1965年提出［5］。它不需要建立控制对象的精确的数学模型，只要求把现场工作人员的经验和数据总结成较完善的语言控制规则，因此它能绕过对象的不确定性、不精确性、噪声以及非线性、时变性等的影响。它的知识模型是由一组模糊推理产生的规则(主要由模糊控制规则和表示对象特性的语言规则)构成的，它的人机对话能力强，能够方便的将专家的经验与思考加入到模型中。一般，一个模糊推理系统就是指一个模糊控制器。

模糊控制器由模糊器、推理机和解模糊器组成，框图如图3所示。

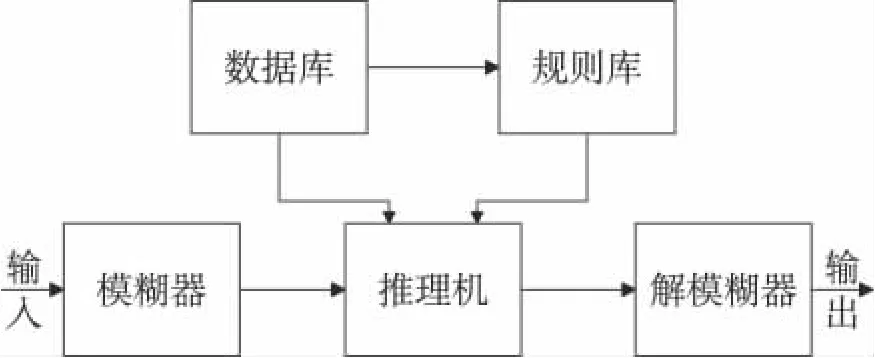
图3 模糊控制器的组成框图

图3中，模糊器:将真实输入的精确量转换为模糊量。推理机:模糊控制器的核心，它具有模拟人的基于模糊概念的推理能力。该推理过程是基于模糊逻辑中的蕴含关系及推理规则来进行的，常用的有Mamdani极小运算法和拉森乘积运算法等。解模糊器:将模糊推理得到的控制量(模糊量)变换为实际用于控制的清晰量。

2.2 模糊PI控制器设计

模糊控制器在矢量控制系统中作为速度调节器，输入变量为电机的速度误差e和速度误差变化率ec，输出控制变量为u，分别对应模糊控制器中的模糊变量 E，EC和 U［6］。根据 PI参数 KP和 KI与 E 和 EC之间的模糊关系，以ΔKP，ΔKI作为输出量，从而调整这2个参数以满足不同的E和EC对PI控制参数的不同要求，从而使系统具有良好的动、静态性能。异步电机的模糊矢量控制框图如图4所示。

图4 异步电机模糊控制框图

E，EC的模糊集合可表示为:{NB，NM，NS，Z，PS，PM，PB}或{负大，负中，负小，零，正小，正中，正大}，理论域值为(－3，3)。确定模糊变量的隶属度函数后，就可以对模糊变量赋值。

在模糊PI控制器参数自整定的过程中，对于不同的|e|和|ec|，比例增益KP和积分增益KI应满足以下要求［7］:

(1)当|e|较大时，为了能加快系统的响应速度，应取较大的KP;同时为了防止系统响应出现较大的超调，应对积分作用加以限制，通常取较小的KI。

(2)当|e|和|ec|处于中等大小时，应分2种情况:若e和ec同号，被控量朝着偏离给定值的方向变化，为了使系统响应具有较小的超调，KP应取得大一些，KI则应取得适当大;若e和ec异号，被控量朝着接近给定值的方向变化，此时应逐渐减小KP和KI。

(3)当|e|较小时，为了使系统有良好的稳态性能，应适当弱化比例作用，加强积分作用甚至将KI设为最大值，以防止e的微小变化致使系统震荡。

(4)|ec|越大，KI越大，反之亦然。

在综合上述专家知识的基础上，采用三角形的隶属度函数［8］，进行大量仿真实验调试后，得到调整量ΔKP，ΔKI的控制规则如下表1所示。

3 仿真与分析

在异步电机控制系统的仿真模型上，对异步电机的模糊PI的控制算法进行了仿真测试。在Matlab/Simulink中，异步电机选用的鼠笼电机模型，电机仿真参数:额定功率PN=2.2 kW，额定电压UN=220 V，频率 f=50 Hz，定子电阻 Rs=0.8 Ω，转子电阻 Rr=0.816 Ω，定子自感Ls=71 mH，转子自感Lr=71 mH，定、转子互感Lm=69 mH，极对数np=2，转动惯量J=0.18 k g·m2。

在Matlab/Simulink中，系统仿真模型如图5所示。仿真条件:给定额定转速(1500 r/min)，电机空载启动，0.2 s后给定50%的额定负载(5 N·m)。仿真结果如图6、图7、图8所示。

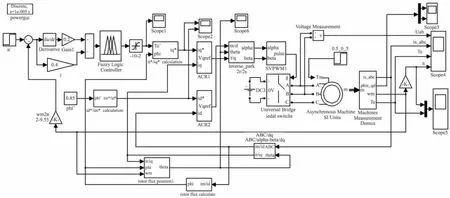
图5 采用模糊PI控制器的电机控制系统仿真模型

图6 电机转速波形

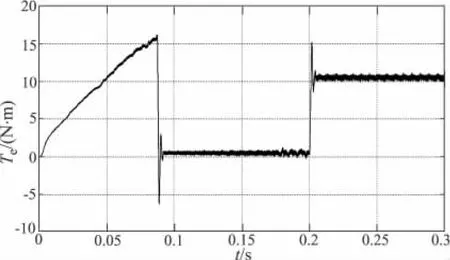
图7 电机电磁转矩波形

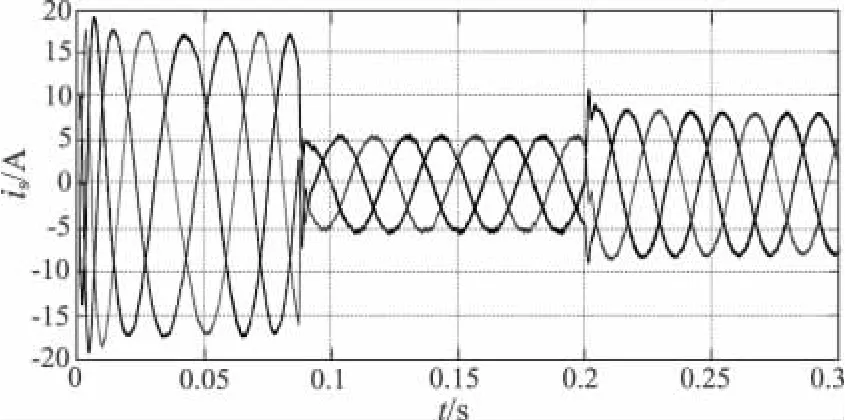
图8 电机定子电流波形

分析图6～图8可知，给定1500 r/min，空载启动电机时，0.088 s后电机达到稳态，启动电流为17.5 A，在限定范围内。启动最大转矩为17.5 N·m，启动转矩为额定转矩的1.75倍，在系统要求的范围内。在0.2 s时突加50%的额定负载，则加载0.025 s以后，电机即进入稳定运行状态(转速恒定、转矩稳定)。在突加负载过程中，转矩波动仅8%。系统在突加阶跃负载环境下的过渡过程，控制系统能保持转速恒定，响应快速，抑制电磁转矩脉动。同时电机转速保持恒定为1500 r/min，鲁棒性能好。

4 结论

本文研究基于模糊控制的异步电机矢量控制系统，在矢量控制系统的速度闭环中采用模糊控制。仿真研究表明，采用模糊控制的矢量控制系统具有良好的稳态性能，可以很好地抑制转速超调。该方法在突变负载情况下，速度基本保持稳定不变，系统鲁棒性大大增强，说明该控制方法的正确性和可行性。但是电机矢量控制系统中磁链闭环没有应用模糊控制，有待于进一步研究，同时对于仿真的启动过程也可以再深入研究。

［1］Chau K T，Chan C C.Emerging energy － efficient technologies for hybrid electric vehicles［J］.Proceedings of the IEEE，2007，95(4):821-835.

［2］张春喜，廖文建，王佳子.异步电机SVPWM矢量控制仿真分析［J］.电机与控制学报，2008，2(12):160-163.

［3］杨 勇.基于模糊自整定的改进型永磁同步电机矢量控制仿真研究［J］.机电工程技术，2010，39(8):47-49.

［4］陈伯时.电力拖动自动控制系统［M］.北京:机械工业出版社，2005.

［5］孙文焕.基于FPGA的全数字化交流变频调速系统［D］.武汉:华中科技大学，2000.

［6］杨 明，张 扬，曹何金生，等.交流伺服系统控制器参数自整定及优化［J］.电机与控制学报，2010，14(12):29-33.

［7］刘金琨.先进PID控制MATLAB仿真［M］.北京:电子工业出版社，2011.

［8］洪 跃，刘宝运，金士良，等.模糊控制在液体粘性离合器中的应用［J］.机械设计与研究，2008，24(1):58-67.

［9］王 研，杜军红，陶伟宜，等.基于DSP的空间电压矢量法PWM 的研究［J］.电机与控制学报，2000，4(2):98-101.

［10］满春涛，张凯博，金祯伊.SVPWM变频空调永磁同步压缩机控制系统［J］.哈尔滨理工大学学报，2011，16(04):82-85.

［11］张永昌，赵争鸣.基于自适应观测器的异步电机无速度传感器模糊矢量控制［J］.电工技术学报，2010，25(3):40-47.

［12］BOWES SR，LIU YS.The relation between space-vector modulation and regular sampled PWM ［J］.IEEE Trans on IE，2007，44(5):670-679.