援越抗法战争中的中法博弈*——基于不完全信息动态博弈模型

康 甫

(中国人民大学国际关系学院，北京 100872)

一、援越抗法战争的历史

由于自然资源丰富，战略位置重要，印度支那地区，包括越南、老挝、柬埔寨在内是传统的殖民地地区，越南是其中最大的国家，也是印度支那问题的核心。1884年开始该地区成为法国的殖民地。在第二次世界大战期间，由于法国被德国法西斯占领，失去了对印度支那地区的控制，由日本代替其在印度支那地区的存在。但实际上，法国从未主动放弃过殖民地统治的意图，只是由于自身实力所限，暂时搁置了对印度支那地区的控制。1945年7月，二战即将结束之前，盟国在波茨坦会议上就印度支那问题达成一项协议，规定以北纬16度线为界，北纬16度线以北地区属中国战区，以南划归英国东南亚司令部辖区。这种划分的主要理由是为了对日作战的需要。1945年8月15日，日本宣布投降，二战结束。越盟胡志明主席在河内发表“独立宣言”，废除了与法国签订的所有旧约，取消了法国在越南的一切特权。但是，越南的独立受到法国的干涉。1945年9月初，盟军军队以解除日军武装和接受日军投降的名义，分别开进北纬16度线以北和以南地区。并在英国的支持下，加快了重返印度支那殖民地的步伐。在英军的支持下，截至1946年1月28日英军撤出为止，法国派出7万远征军开往印度支那，控制了越南、柬埔寨和老挝南部的大部地区。3月6日，法军强行登陆进驻海防，取得了在越南北部地区的第一个立足点。3月18日，法军由海防进入河内。面对拥有现代化装备的法军力量，刚刚成立不久的越南民主共和国难以与其正面对抗。到1949年底，尽管在越南人民坚决抵抗下，粉碎了法军速战速决企图，但战争的主动权仍然掌握在法军手里。1949年10月1日中华人民共和国成立，并对越南展开大力支援，使战争形势彻底改观。1950年1月18日，新中国与越南建交，成为第一个承认越南民主共和国的国家。中国的举动带动苏联、东欧等社会主义国家随后承认越南，越南在政治上获得极大的支持和鼓舞。应越方请求，中国对越南抗法战争给予了大力支持。1950年8月，在以陈赓为首的中国顾问团的帮助下，越南军队发起“边界战役”，打通中越边界，中国成为越南抗法救国的大后方。在1954年具有决定意义的奠边府战役中，中国军事顾问团参与作战计划的制定和决策，为这次战役以及越南抗法战争的最后胜利作出巨大贡献。在1950—1954年间，中国国内虽百废待兴，但还是尽最大努力给予越南经济和军事援助。然而，法国发动越南战争后，新中国的参战是法国始料未及的，而法国在越南战争中的失败更是其没有想到的。可以说，越南抗法战争的胜利得益于新中国无私的援助。

二、以不完全信息动态理论的观点看待中法博弈

博弈论是研究决策主体的行为发生直接相互作用时候的决策以及这种决策的均衡问题的。也就是说，当一个主体，好比说一个人或一个企业的选择受到其他人、其他企业选择的影响，而且反过来影响到其他人、其他企业选择时的决策问题和均衡问题。博弈论的决策主体可以是个人、企业、国家等。当国家成为博弈论的决策主体时，国际关系即成为国家间博弈。如果将国家看作理性的人格化主体，采用博弈论分析国际关系是再恰当不过的。博弈论的基本概念包括:参与人、行动、信息、战略、支付函数、结果、均衡。参与人，是指博弈中选择行动以最大化自己效用的决策主体。在国际关系中，自然人、企业、团体、民族国家、国际组织等都可以成为国际关系的主体，但在国家间博弈中，主要的参与者是民族国家。行动是参与人的决策变量，是参与人的实际行为。在国际关系中，国家发动不发动战争、实行不实行贸易制裁都可以看做是行动。战略是参与人选择行动的规则，它告诉参与人在什么时候选择什么行动。在国际关系中，战略是一个国家可能采取的行动，例如美苏争霸期间，苏联曾经偷运导弹至古巴，美国要求苏联撤回，而苏联不同意。这时双方都有两种策略选择:美国是挑起战争和不挑起战争;苏联是从古巴撤回和不撤回。信息指的是参与人在博弈中的知识。支付函数是参与人从博弈中获得的效用水平，它是所有参与人战略或行动的函数，是每个参与人真正关心的东西。继续采用古巴导弹危机的例子，如果美国发动战争，那么美国和苏联都将损失大量的资源，而不发动战争，美国则会“丢面子”，在同盟中的威信受到影响。如果苏联撤退，则会使国家荣誉受到伤害;但是如果不撤退，则可能引起美国发动战争。结果是指博弈分析者感兴趣的要素的集合，例如均衡战略组合、均衡行动组合、均衡支付组合等。均衡是所有参与人最有战略的组合，是博弈的最终结果，例如纳什均衡等。

根据不同的划分标准，博弈可以划分为不同的类型。从参与人行动的先后顺序可以分为静态博弈和动态博弈。静态博弈指的是，博弈中参与人同时选择行动，或虽非同时但后行动者并不知道前行动者采取了什么具体行动;动态博弈指的是，参与人的行动有先后顺序，且后行动者能够观察到先行动者所选择的行动。划分博弈的第二个标准是参与人对有关其他参与人(对手)的特征、战略空间及支付函数的知识。从这个角度，博弈可以划分为完全信息博弈和不完全信息博弈。完全信息指的是每一个参与人对所有其他参与人(对手)的特征、战略空间及支付函数有准确的知识;否则，就是不完全信息。将两个划分标准结合起来，可以得到四种不同类型的博弈，即完全信息静态博弈、完全信息动态博弈、不完全信息静态博弈、不完全信息动态博弈［1］。

在援越抗法战争中，法国在发动越南战争之前，需要进行大量的分析。它担心的一个重要问题是中国是否会参战，援越抗法。中国政府也在是否参与援越抗法战争问题上犹豫不决，中国政府是否参与战争是与法国是否介入战争紧密相关的。也就是说，法国的行动在中国之前，因此这就具有了时间的先后顺序。另外，在这场博弈中，法国对中国的特征、战略空间及支付函数没有准确的了解，因此援越抗法战争中的中法博弈归属为不完全信息动态博弈。那么，根据不完全信息动态博弈理论，将中法两国看作是完全理性的行为主体，两国在这场博弈过程中会采取怎样的行动才是理性的，双方会选择怎样的战略达到怎样的均衡?下面我们就根据不完全信息动态理论对中法博弈进行分析。

在博弈论里，一个博弈可以通过两种不同的方式来表述，一种是战略式表述，一般用来描述静态博弈;另一种是扩展式表述，更适合于描述动态博弈。因此援越抗法战争中，中法博弈可以表述为图1。

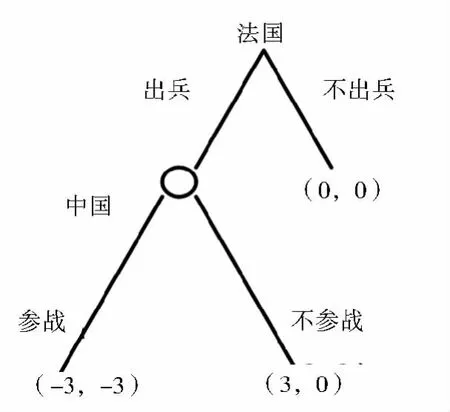
图1 中法博弈过程中的扩展表述

在这个博弈中，法国首先决定是否出兵;在法国决定后，中国决定是否参战。法国有两种选择:出兵或不出兵;中国也有两种选择:参战或不参战。如果法国出兵后中国参战，则两败俱伤;如果法国出兵后中国不参战，法国可以从越南战争中获得好处，中国没有损失也没有收益;如果法国不出兵，那么中国参战还是不参战对双方没有影响，它获得的支付都为零。如果博弈的支付如此，那么中国的最优策略是不参战，因为不管在法国是否出兵的情况下，中国不参战能够获得的支付为0，大于法国出兵、中国参战时能够得到的支付为－3。既然中国最优的策略是不参战，那么法国的最优策略就是出兵，此时它可以获得的支付为3。但实际上，中国和法国的情况都没有如此简单。当时，新中国刚刚建立而且国内百废待兴，政权还相当不稳定，国际上也仅仅获得少数国家承认。然而，法国对越南发起的战争不但是对中国兄弟邻邦的侵略，而且是对中国西南领土的直接威胁，中国参战既是为了援助越南，也是为了保护中国的领土安全，维护中国的核心利益。如果中国能够在这场战争中获得胜利，将大大增强新中国重扬国威的信心，提高中国在社会主义国家阵营中的地位。据此我们对上面提到的博弈支付进行修改，进而可以得到图2。

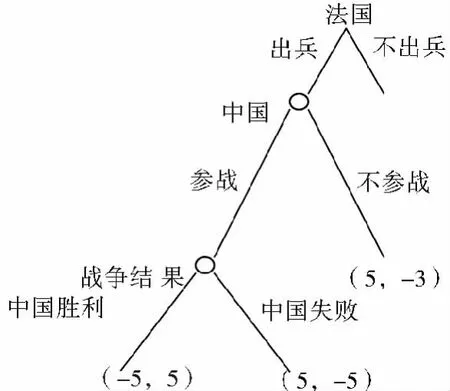
图2 中法博弈过程中的扩展表述

在这个博弈中，只要法国出兵，不论中国是否参战，中国的利益都会受到影响，那么中国将如何决定参战与否呢?我们假定如果中国参战，胜利的概率为p，失败的概率为(1－p)，中国在参战和不参战之间无差异的条件为:

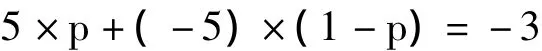
由简单计算可以得到:当p=0.2时，中国在参战和不参战之间无差异。也就是说，只要当p＞0.2时，法国出兵，中国肯定参战。如果p＜0.2，法国出兵，中国也不会参战。

然而，法国政府对新中国政府是否参战估计不足。法国政府一直认为，刚刚建立的新中国经济建设没有恢复，无力援助越南战争，百废待兴的中国不可能卷入战争，而且法国人认为中国军队没有坦克、大炮、飞机、军舰，装备很差的中国即使参加战争也不会对法国构成威胁。1954年3月30日，北越在奠边府发动全面进攻，抢占两个外围制高点，使用的是中国自朝鲜战争后调来的大炮，法军没有预料它会有这种大炮［2］。法国人轻敌的表现使法国在越南战争中损失惨重，丢尽了脸面。

同样，根据不完全信息动态博弈理论，我们可以利用这个博弈中的支付函数对法国的行为进行分析。假定法国估计中国参战的概率为q，中国胜利的概率为p，那么法国出兵好于不出兵的条件为:q×［(－5)×p+5×(1－p)］+5×(1－q)＞0，

简单计算得:5－10pq＞0

也就是说，只要pq＜0.5，法国肯定会出兵。而根据当时法国的估计，中国出兵的可能性很小，即q很小，中国取胜的可能性也很小，即p很小，在这种情况下，根据博弈论理论推理，法国出兵实际上是一个较为理性的决策，尽管法国遭受了巨大的损失。

三、结论

通过运用不完全信息动态模型的分析，法国在中法博弈的过程中出兵是较为理性的选择。但实际上，法国发动的第一次印度支那战争是逆历史潮流的，法国的侵略战争是非正义的，是注定要失败的。历史表明，在中国的援助下，越南在第一次印度支那战争中获胜。1954年7月21日，在以周恩来为首的中国政府代表团的努力斡旋下，日内瓦会议就恢复印度支那和平问题达成协议，从而结束了持续8年多的越南抗法战争。

越南抗法战争的胜利是西方殖民主义势力在亚洲的一次重大失败，法国从印度支那地区的撤退，标志着旧的殖民体系的瓦解和殖民主义灭亡是不可避免的。弱小国家只要坚持团结，坚持斗争，一定能战胜大国的侵略，赢得独立。历史表明，强权政治和霸权主义是必然要失败的，用武力来解决国际争端是行不通的。

自从上个世纪中后期博弈论被引入国际关系研究开始，博弈论为研究国际政治提供了一种新方法。例如莫顿·A．卡普兰(Kaplan，M．A．)在1957年出版的《国际政治的系统和过程》中，有三章关于国家之间的对策分析，所采用的方法完全是博弈论①该书第九、十、十一章中有大量的篇幅是关于博弈论的，包括博弈论的基本知识以及在国家之间关系的对策运用等。。托马斯·谢林(Shelling，Thomas)在1980年出版的《冲突的策略》中也大量运用了博弈论的分析方法［3］。正如莫顿·卡普兰所说:“有关在国际政治中选择模式稳定性限度的问题，博弈论迄今为止还不能提供太多的东西。尽管博弈论所提供的是重要的，但还不够系统。”“博弈论尚未解决策略的最重要的问题，尤其是国际政治领域内出现的种种策略问题。但是，它仍不失为一个精确工具，一个仅限于采用有明确假定的工具。”［4］可以说，对博弈论的运用一定程度上弥补了国际政治研究定性分析的不足，但由于它的局限性，在运用博弈论模型解决国际关系问题的同时，必须综合考虑更多的因素，对问题进行多角度、多方法的讨论是不可或缺的。

［1］张维迎．博弈论与信息经济学［M］．上海:上海人民出版社，1996:12－13．

［2］［美］亨利·基辛格．大外交［M］．海口:海南出版社，1998:607－608．

［3］Thomas C．Schelling，The Strategy of Conflict，Cambridge:Harvard University Press，1980．

［4］［美］莫顿·卡普兰．国际政治的系统和过程［M］．上海:上海人民出版社，2008:211．