具有执行器故障的非线性系统可靠控制设计

李爱晨，李香善，焦建宇，张 友

（东北师范大学 计算机科学与信息技术学院，长春130117）

在实际工业生产过程中，电气控制系统的执行器经常发生失效现象，因此针对具有执行器失效的控制系统进行可靠控制器设计应用广泛［1－2］.目前已有的相关设计目的都是为具有执行器故障的线性控制系统设计一种固定增益参数的控制器，它能保证整个控制系统在部分执行器失效情况下的渐近稳定性，但对于具有执行器故障的非线性系统相关可靠控制器设计问题不能保证控制系统的渐近稳定性.文献［3－5］运用基于T－S模糊模型的建模方法进行了具有执行器故障的非线性系统相关可靠控制器设计研究.T－S模糊模型是控制领域研究复杂非线性系统的一种有效数学工具，目前已成功应用于若干个实际控制系统设计中，解决了许多非线性系统控制综合问题［6－9］.在基于T－S模糊模型的控制综合领域，多数研究成果均采用文献［6］提出的并联分布补偿技术（简称PDC技术）进行系统控制器设计.但基于PDC技术所得的控制条件常具有较大的保守性，因此很大程度上限制了T－S模糊模型在控制领域的应用.Guerra等［10］针对离散时间T－S模糊系统控制问题提出了非并联分布补偿技术（简称非－PDC技术）.非－PDC技术通过改变控制器架构可引入更大的设计自由度，极大减少了控制设计的保守性.在非－PDC技术设计思想的启发下，文献［11－14］提出了保守性越来越小的镇定控制条件，但保守性问题仍未得到彻底解决，不仅在控制器设计上，在其他方面也要进行改进，以进一步减少控制设计的保守性.

本文考虑具有执行器故障离散时间非线性系统的基于T－S模糊模型的可靠控制设计问题，与已有相关研究成果相比，本文在非－PDC技术设计思想的启发下，提出了能引入更多控制增益矩阵变量的新型可靠控制器，并在结果证明过程中提出了一种新的自由矩阵变量技术.结果表明，本文方法显著降低了控制设计的保守性，获得了比已有方法保守性更小的可靠控制器设计条件.

1 预备知识

1.1 基于T－S模糊模型具有执行器故障的离散时间非线性系统

考虑如下一类具有执行器故障的离散时间T－S模糊控制系统：

其中：x（k）表示n维系统状态向量；u（k）表示控制系统的m维执行器向量；Ai和Bi表示适当维数的系统参数矩阵；wL表示执行器发生故障信息的标识矩阵；hi（θ（k））表示T－S模糊模型的模糊隶属函数；r表示模糊模型规则数.

不失一般性，标识矩阵wL的组成结构可表示为

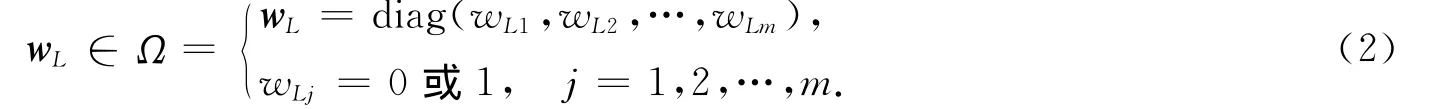
若wLj＝0，则表示第j个执行器发生故障.于是，对于拥有m个执行器的系统，执行器正常或部分发生故障的可能情况有2m－1种，即集合Ω中由2m－1个矩阵组成，因而有L＝1，2，…，2m－1.

定义1 若在执行器正常或部分发生故障可能的2m－1种情况下具有执行器故障的离散时间T－S模糊控制系统（1）都是全局渐近稳定的，则称带有执行器故障的离散时间T－S模糊系统（1）是可靠稳定的.

1.2 新型可靠控制器的设计

为了保证具有执行器故障的离散时间T－S模糊控制系统（1）的可靠稳定性，文献［6］基于PDC技术提出了一种模糊状态反馈控制律，即

得到了基于线性矩阵不等式条件下的可靠控制器设计条件，但文献［6］给出的设计方法存在较大的保守性.为了进一步减少上述结果的保守性，本文基于非－PDC技术提出一种新型可靠控制器：

其中：

与文献［6］提出的状态反馈控制律相比，新型可靠控制器（3）具有全新的控制架构，能引入二倍的控制增益矩阵（Fi和Gi）.为了配合这种全新的控制架构，本文提出了一个与之匹配的Lyapunov函数和一种自由矩阵变量技术，显著增加了可靠控制设计过程中的自由度，并得到保守性更小的可靠控制器设计条件.

引理1［10］对于对称正定矩阵P＞0和P＋＞0，矩阵不等式ATPA－P＜0成立的充分条件是存在一个适当维数的矩阵使得如下矩阵不等式成立：

2 主要结果

为进一步减少已有具有执行器故障的离散时间T－S模糊控制系统可靠控制器设计的保守性，本文基于非－PDC技术提出一种新型可靠控制器（3），并提出了一种新的自由矩阵变量技术，可将不同模糊子模型间的耦合关系映射到若干个组合大矩阵中，因此在可靠控制器设计过程中能更有效地考虑模糊隶属函数的有用信息，减少控制条件的保守性.

则具有执行器故障的离散时间T－S模糊控制系统（1）在新型可靠控制器（3）的控制下是可靠稳定的.

证明：对在新型可靠控制器（3）控制下的具有执行器故障的离散时间T－S模糊控制系统（1）考虑如下Lyapunov函数：

对式（7）沿时间方向求取一阶差分函数，可得

其中

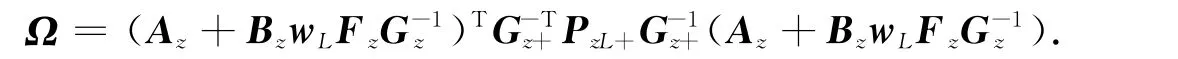
由Lyapunov稳定性定理可知：具有执行器故障的离散时间T－S模糊控制系统（1）是可靠稳定的充分条件为如下矩阵不等式成立：

对不等式（10）使用引理1，可得能保证矩阵不等式（10）成立的充分条件为如下矩阵不等式成立：

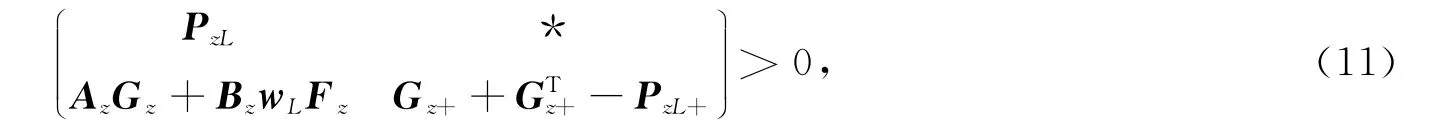
其中：

整理不等式（11）左侧，有

其中：

此时，若线性矩阵不等式（4）和（5）成立，则有

将线性矩阵不等式（6）两边分别左乘（h1I … hrI）右乘（h1I … hrI）T可得

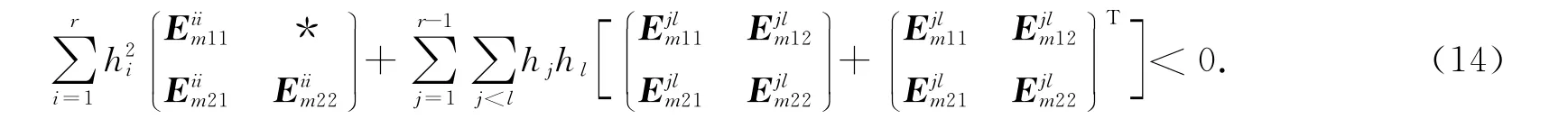
结合矩阵不等式（13）和（14），易得如果线性矩阵不等式（4）～（6）成立，则矩阵不等式（11）也成立，即具有执行器故障的离散时间T－S模糊控制系统（1）在新型可靠控制器（3）的控制下是可靠稳定的.证毕.

注1 通过设计与新型可靠控制器相匹配的Lyapunov函数构造及提出一种新的自由矩阵变量技术，定理1得到了保守性更小的具有执行器故障的离散时间T－S模糊控制系统（1）的可靠控制器设计条件.特别地，自由矩阵变量的成功引入将各个模糊子模型间的耦合关系映射到若干个大矩阵（6）中，上述方法能更有效地考虑模糊隶属函数的有用信息，显著减少结果的保守性.

3 仿真实验

考虑如下形式的一类离散时间非线性控制系统：

按照T－S模糊建模方法，令

则离散时间非线性控制系统（15）可由如下离散时间T－S模糊系统表示：

其中：

为了验证本文提出的可靠控制器设计方法的有效性，本文在仿真实验中分别使用文献［6］给出的已有方法和本文定理1提出的方法进行对应可靠控制器的设计.结果表明：文献［6］提出的设计方法只能在β≤1.68时才能保证带有执行器故障的离散时间T－S模糊控制系统（1）是可靠稳定的可行解；而定理1得到的结果是β≤1.71.由此，本文提出的新型可靠控制器及相关技术措施在减少保守性方面均有效.

令β＝1.70，此时只有本文方法能提供可靠控制器设计方案.利用Matlab计算软件可得满足线性矩阵不等式（4）～（8）条件下的控制增益矩阵F1，F2，G1，G2.

图1 状态变量x1（k）的轨迹Fig.1 Trajectory of the state variable x1（k）

图2 状态变量x2（k）的轨迹Fig.2 Trajectory of the state variable x2（k）

图3 控制输出量u1（k）的轨迹Fig.3 Trajectory of the control input u1（k）

综上所述，本文针对具有执行器故障的离散时间非线性系统的可靠控制问题提出了一种新型的可靠控制器设计方案.在非－PDC技术设计思想的启发下，所设计的新型可靠控制器能引入更多控制增益矩阵，从而增加了控制设计过程的自由度.此外，还提出了一种自由矩阵变量技术，它能将各个模糊子模型间的耦合关系映射到若干个大矩阵中，通过更有效地考虑模糊隶属函数的有用信息进一步减少了可靠控制器设计条件的保守性.仿真实验验证了本文提出方法的有效性和可行性.

［1］YANG Guang－hong，WANG Jian－liang，Soh Y C.Reliable H∞Controller Design for Linear Systems ［J］.Automatica，2001，37（5）：717－725.

［2］LIAO Fang，WANG Jian－liang，YANG Guang－hong.Reliable Robust Flight Tracking Control：An LMI Approach［J］.IEEE Transactions on Control Systems Technology，2002，10（1）：76－89.

［3］WU Huai－ning.Reliable LQ Fuzzy Control for Nonlinear Discrete－Time Systems via LMIs［J］.IEEE Transactions on Systems，Man，and Cybernetics，2004，34（2）：1270－1275.

［4］WU Huai－ning.Reliable LQ Fuzzy Control for Nonlinear Continuous－Time Systems with Actuators Faults［J］.IEEE Transactions on Systems，Man，and Cybernetics，2004，34（4）：1743－1752.

［5］WU Huai－ning，ZHANG Hong－yue.Reliable H∞Fuzzy Control for a Class of Discrete－Time Nonlinear Systems Using Multiple Fuzzy Lyapunov Functions［J］.IEEE Transactions on Circuits and SystemsⅡ：Express Briefs，2007，54（4）：357－361.

［6］Wang H O，Tanaka K，Griffin M F.An Approach to Fuzzy Control of Nonlinear Systems：Stability and Design Issues［J］.IEEE Transactions on Fuzzy Systems，1996，4（1）：14－23.

［7］Kim E，Lee H.New Approaches to Relaxed Quadratic Stability Condition of Fuzzy Control Systems［J］.IEEE Transactions on Fuzzy Systems，2000，8（5）：523－534.

［8］LIU Xiao－dong，ZHANG Qing－ling.New Approaches to H∞Controller Designs Based on Fuzzy Observers for T－S Fuzzy Systems via LMI［J］.Automatica，2003，39（9）：1571－1582.

［9］Montagner V F，Oliveira R C L F，Peres P L D.Convergent LMI Relaxations for Quadratic Stabilizability and H∞Control of Tanaki－Sugeno Fuzzy Systems［J］.IEEE Transactions on Fuzzy Systems，2009，17（4）：863－873.

［10］Guerra T M，Vermeiren L.LMI－Based Relaxed Nonquadratic Stabilization Conditions for Nonlinear Systems in the Takagi－Sugeno’s Form ［J］.Automatica，2004，40（5）：823－829.

［11］Kruzewski A，Wang R，Guerra T M.Nonquadratic Stabilization Conditions for a Class of Uncertain Nonlinear Discrete Time TS Fuzzy Models：A New Approach［J］.IEEE Transactions on Automatic Control，2008，53（2）：606－611.

［12］DING Bao－cang.Homogeneous Polynomially Nonquadratic Stabilization of Discrete－Time Takagi－Sugeno Systems via Nonparallel Distributed Compensation Law ［J］.IEEE Transactions on Fuzzy Systems，2010，18（5）：994－1000.

［13］Lee D H，Park J B，Joo Y H.Improvement on Nonquadratic Stabilization of Discrete－Time Takagi－Sugeno Fuzzy Systems：Multiple Parameterization Approach［J］.IEEE Transactions on Fuzzy Systems，2010，18（2）：425－429.

［14］ZHANG Hua－guang，XIE Xiang－peng.Relaxed Stability Conditions for Continuous－Time T－S Fuzzy－Control Systems via Augmented Multi－indexed Matrix Approach［J］.IEEE Transactions on Fuzzy Systems，2011，19（3）：478－492.