无驱动微机械陀螺敏感元件模态分析

张增平，张福学，张 伟，刘 宇，张 宁

（北京信息科技大学 传感技术研究中心，北京 100101）

无驱动微机械陀螺敏感元件模态分析

张增平，张福学，张 伟，刘 宇，张 宁

（北京信息科技大学 传感技术研究中心，北京 100101）

鉴于常规微机械陀螺的驱动结构和检测结构往往需要进行频率匹配，造成带宽较窄，工艺复杂的问题，设计了一种新的微机械陀螺，安装于旋转飞行器上，利用飞行器的旋转获得角动量，敏感飞行器的偏航和俯仰横向角速度。由于没有驱动结构，所以结构简单，带宽较宽。首先基于这种巧妙的结构建立了敏感元件的振动方程。根据振动方程，扭转梁是影响质量振动模态和模态频率的关键，同时考虑到应力、残余应力的释放以及工作能力，扭转梁设计成横截面积为矩形的弧形梁，并对其抗扭刚度进行了解析推导和计算，从而确定了敏感元件的固有频率。接着利用有限元分析的方法，对其振动模态进行了仿真，仿真结果表明，敏感元件的第一模态是扭转振动，固有频率相对于解析结果的误差为9.86%。为了进一步验证，设计了静电驱动电容检测的方法，实验测试得到的谐振频率和解析值的相对误差为5.21%。仿真和实验结果与理论计算一致，表明扭转梁的设计是合理的，模态分析是正确的，而且为动态性能评估和结构优化提供了理论依据。

敏感元件；扭转梁；扭转刚度；固有频率

目前，微机械（MEMS）陀螺一般都是利用科氏效应敏感载体角速度的振动式陀螺。它们的工作原理都是由弹性挂件将检测质量块悬挂在基座上，产生振动，敏感输入角速度[1-4]。通常为了获得最大位移，设计中往往通过匹配驱动结构和敏感结构的谐振频率，使得陀螺工作在谐振点处。结果，系统中引起频移的各种变量，很容易被陀螺敏感，引入误差。在高品质因子条件下，灵敏度较高，但是带宽较窄。为了避免目前微机械陀螺的这种局限性，文中设计了一种新型的无驱动微机械陀螺，它没有驱动结构，所以具有加工工艺简单、成本较低、重复性好、抗冲击性能可靠等优点[5-8]。

另外，以模态分析为基础的结构动态设计，是近年来振动工程界开展的最广泛的研究领域之一。众所周知，传统的结构设计，在考虑动态因素的结构修改时，是以经验和反复实测为主要手段，这大大减缓了设计速度，设计质量也难以达到最优。有限元法(FEM)为结构动态设计提供了重要的途径[9-11]。无驱动微机械陀螺的敏感元件的设计，要求各阶模态频率远离工作频率，应使其不影响结构正常工作为佳。

1 动力学模型

1.1 结构原理

图1是无驱动微机械陀螺的结构原理图，它采用体微深刻蚀工艺技术加工制作而成。

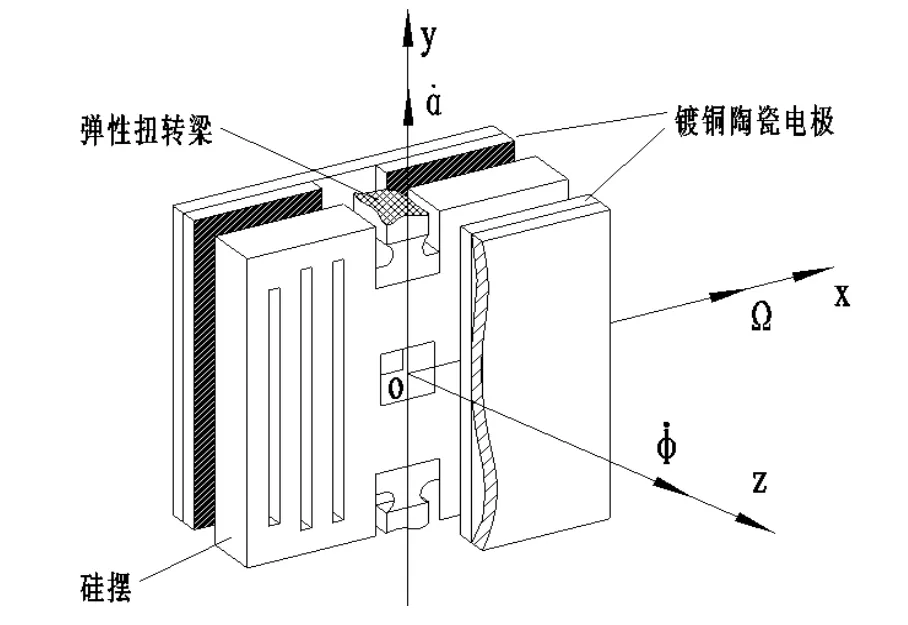
图1 陀螺结构原理图Fig.1 Schematic diagram of gyro structure

图1显示，中间部分是单晶硅材料的敏感元件块，我们称为敏感元件。敏感元件的上下两端是弹性扭转梁，它与陀螺的外框固连，敏感元件绕着这一约束中心可以产生振动，因此敏感元件只有一个自由度。陀螺安装在旋转飞行器上，选择坐标系oxyz固定于敏感元件上，原点位于敏感元件的质心；z轴与载体飞行器的纵轴重合，称为驱动轴；y轴位于敏感元件的约束中心称为输出轴；x轴位于飞行器横截面内，称为输入轴；α˙是敏感元件绕输出轴振动的角速度，φ˙是飞行器绕驱动轴旋转的角速度，Ω是飞行器转动的横向角速度。当陀螺随着飞行器以φ˙的角速度旋转时，飞行器同时发生横向角速度Ω的转动，敏感元件受到周期性变化的科里奥利力的作用，使敏感元件绕着输出轴振动，振动角速度为α˙。

敏感元件两侧是陶瓷片，通过溅射工艺在陶瓷片对称轴线的两侧溅射铜，形成四个对称的检测电极，检测电极和敏感元件构成差动电容，通过电容拾取电路输出一个幅值和被测角速度成比例的电信号。

1.2 敏感元件角振动方程

这种运动属于刚体绕定点的运动，可以用欧拉动力学方程来推导其运动方程式。为了研究运动，选择四个坐标系。如图2所示，oξης是惯性坐标系，o x1y1z1是偏航或俯仰坐标系， ox2y2z2是飞行器自旋坐标系，oxyz是与敏感元件相固连的动坐标系。

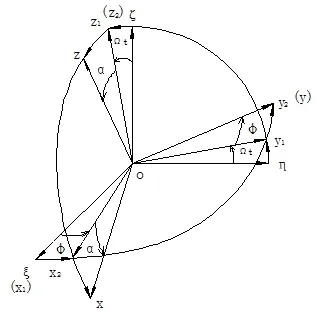
图2 坐标变换Fig.2 Transformation of coordinates

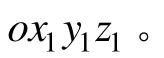
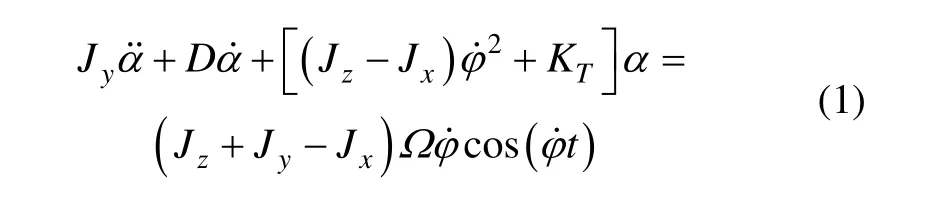
式中， Jx、Jy、Jz是敏感元件相对于x、y、z轴的转动惯量，KT是敏感元件扭转梁的抗扭刚度系数，D是阻尼系数。

图3是敏感元件的几何结构，敏感元件利用扭转梁与外框架固定连接。

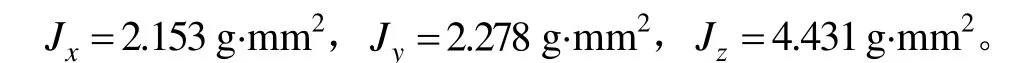
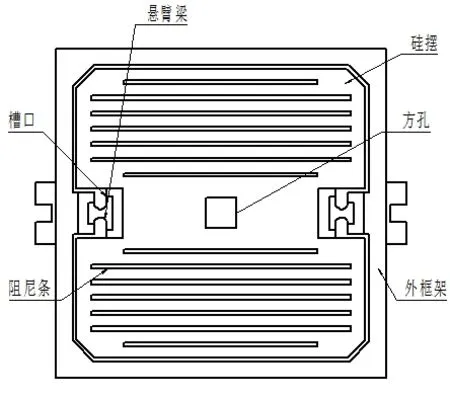
图3 敏感元件结构Fig.3 Si pendulum structure

1.3 角振动方程的解

令

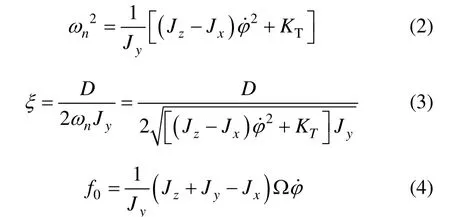
将式(1)化简为：

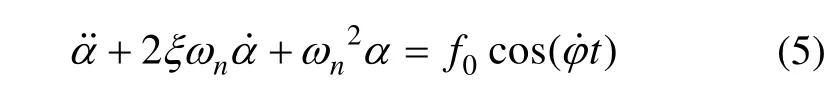
式(5)是一个二阶常微分方程，它的稳态解为：

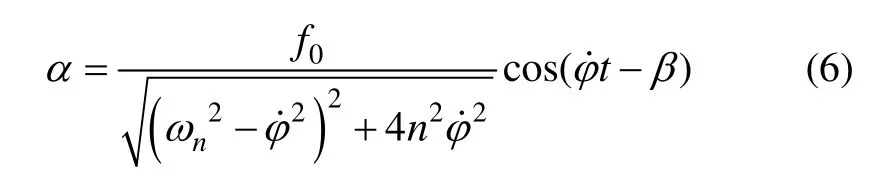
将式(2)(3)(4)代入式(6)可得：

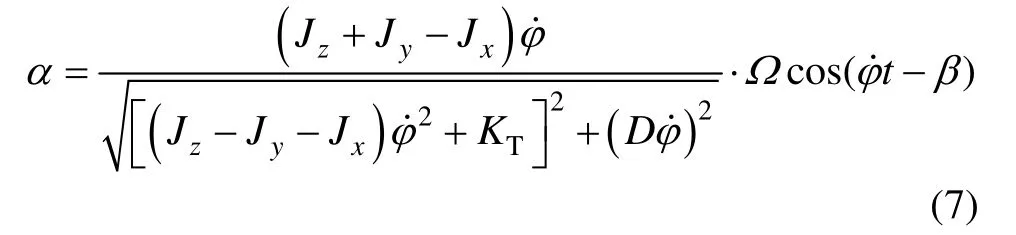
则角振动振幅为：

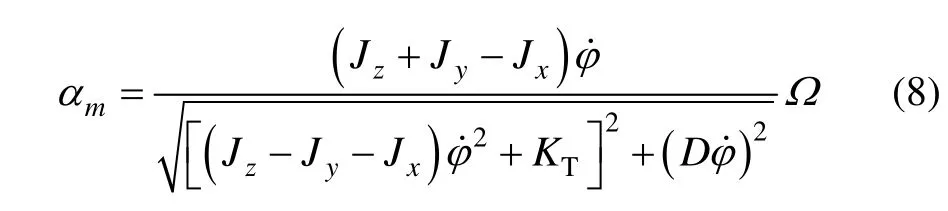
式(8)表明，角振动振幅和被测角速度成正比例，刚度系数 KT不仅影响比例系数，而且是决定角振动模态的关键。所以，接下来，围绕刚度系数对扭转梁进行分析，并就刚度系数解析推导和对振动模态参数固有频率进行分析和计算。

2 扭转梁

图4是扭转梁的结构示意图，设曲率半径为R，y轴的原点选在梁的质量中心，方向平行于圆弧的直径。

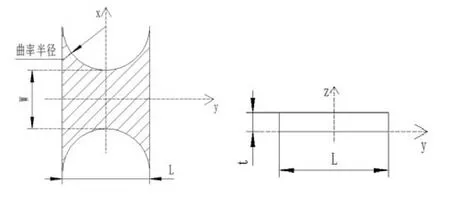
图4 梁结构Fig.4 Beam structure

为了便于推导敏感元件扭转梁的扭转刚度，根据图4作合理的假定：扭转振动的扭转角大小与扭转梁长度成正比，扭转梁所有横截面的翘曲都相同，扭转梁两端连接处的扭转力矩大小相等，方向相反。

2.1 扭转刚度

在上述假定条件下，由弹性力学可知矩形截面扭转梁的扭转刚度为：

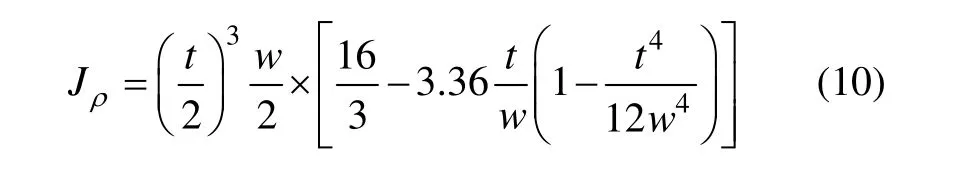
式中，w是坐标y点处的梁宽，是关于y的函数。

由图4可知：

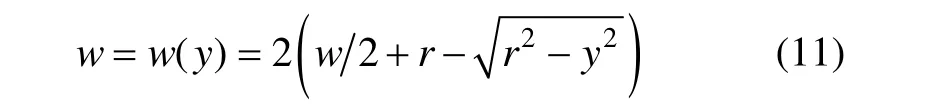
又根据材料力学可知，矩形梁的柔度为作用于轴两端上单位力矩所扭转的角度，并且等于扭转刚度的倒数，则有：

将CEUS分为两个过程，即增强期与消退期，以周围肌壁为参照物，若病灶达峰时间早于周围子宫肌壁，为早增强；反之，为晚增强；消退期同理判断。增强强度高于肌壁为高增强；反之为低增强。

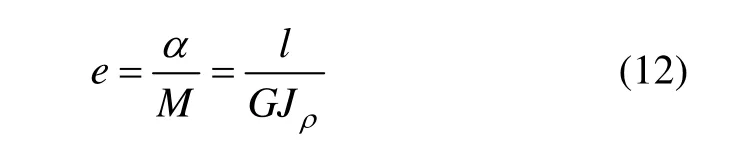
式中，e为柔度，α为扭转角，M为扭矩。

采用微分的方法，对式(12)两边取关于y的微分，有：

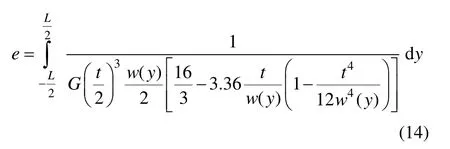
取式(14)倒数，计算后可得扭转刚度为：

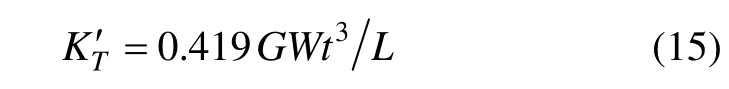
则两端总的扭转刚度为：

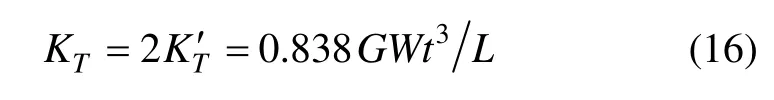
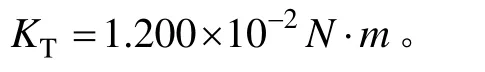
2.2 固有频率

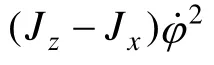
3 模态分析

根据敏感元件的结构尺寸和单晶硅相应的材料常数，定义单元类型为SOLID45。选择国际单位制，弹性模量 EX= 130.2GPa，泊松比 PRXY= 0.279，材料密度 DENS= 2.34g/cm3。建模后的几何图形如图 5，两端是弹性扭转梁，中间是带阻尼条的振动硅片。

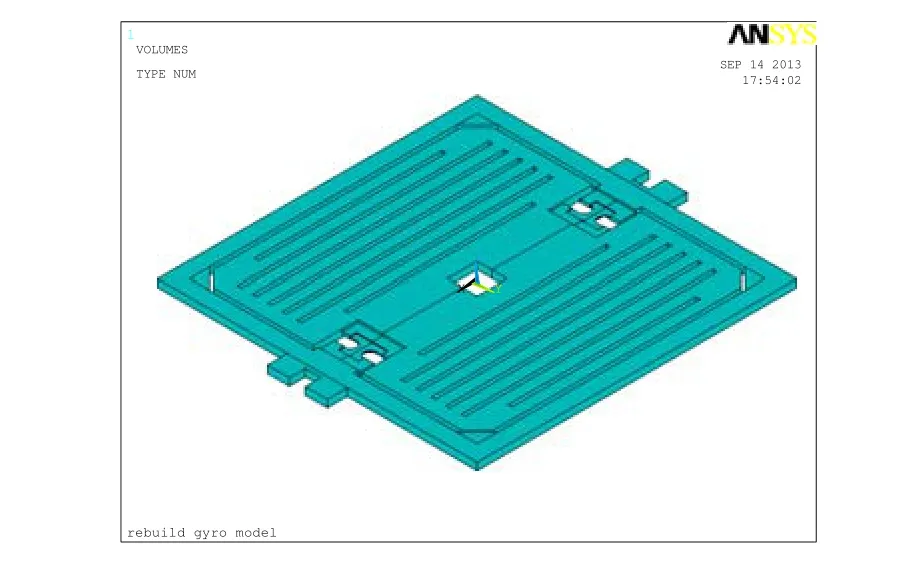
图5 敏感元件实体模型Fig.5 Entity model of Si pendulum

3.2 有限元求解

网格划分之后，在敏感元件的外框上施加全方位位移约束。分析类型选择模态分析，经过求解和后处理，得到如图6的主振型。图6显示，敏感元件的第一模态的振型为振动质量绕着两端梁形成的约束中心做扭转振动，振动的固有频率为329 Hz，相对于理论计算结果365 Hz的相对误差为9.86%。

图6 主振型Fig.6 The main modal

4 实验验证

4.1 实验原理

实验原理是利用静电力模拟敏感元件所受到的科里奥利力，使敏感元件发生振动，通过扫频检测，测量输出信号最大幅值所对应的频率，即为谐振频率。

图7是实验原理示意图，在一侧铜电极上加载电压信号Vd1和Vd2作为静电力模拟。另一侧m和n作为差动电容检测电极。

Vd1和Vd2是一对推挽电压信号，记为：

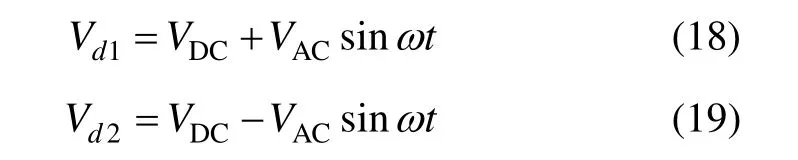
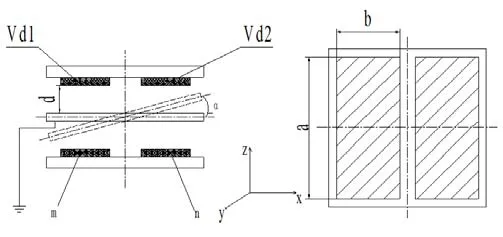
图7 实验原理示意图Fig.7 Experimental schematic diagram

式中，VDC是直流偏置电压，VAC是幅值，ω是角频率。

敏感元件在静电力作用下，转动角度为α，则静电力矩为：

进而推挽信号产生总的扭转力矩为：

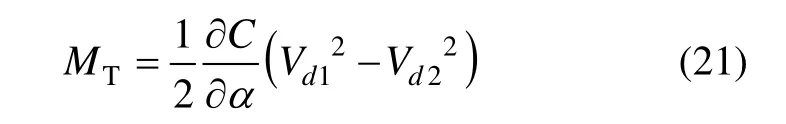
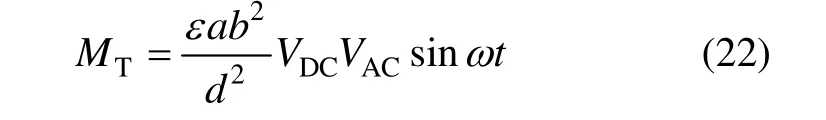
式(22)表明，加载的推挽驱动电压信号，在敏感元件上形成的静电驱动力矩是一个交变力矩，幅值由陀螺尺寸参数和电压的直流偏置以及幅度决定，是一个常数。频率与驱动电压信号相同，所以满足实验测试的输入激励要求，可以很方便地改变驱动信号的频率来调节输入激励的频率，来测量敏感元件振动的幅频特性，从而确定谐振频率。

驱动力矩使敏感元件振动质量块绕着扭转梁偏转α角度时，检测电容m和n形成了差动电容，计算可得形如

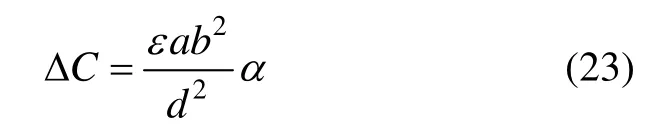
式(23)表明，差动电容和转角成正比，再经过电容电压转换，就可输出和转角成比例的电压信号。

4.2 实验系统及测量结果

实验系统如图8所示，Agilent 81150A信号发生器，用于产生推挽电压信号。

测试时，设置信号发生器为扫频方式，输出信号的频率范围为0~800 Hz。与此同时，进行陀螺输出信号有效值的自动采集与记录。数据经过拟合，得到如图9所示的检测信号有效值随频率变化的关系曲线。

图9显示，被测陀螺的谐振频率为384 Hz。解析值为365 Hz，它们的绝对误差为19 Hz，相对误差为5.21% 。

图8 实验平台Fig.8 Experimental platform

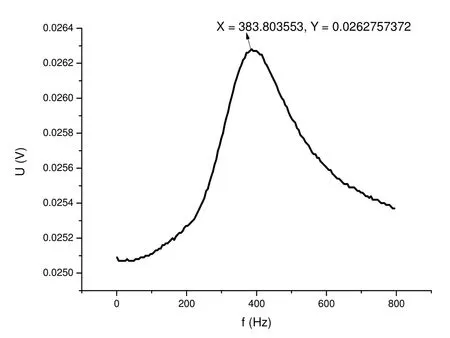
图9 测试曲线Fig.9 Testing curve

5 结 论

无驱动微机械陀螺是一种新型MEMS陀螺，弹性刚度系数是一个重要的动力参数，它决定了振动的固有频率和振型。敏感元件的扭转梁被设计成了横截面为矩形的圆弧形结构。经过数学推导，得出了扭转梁刚度系数和固有频率的解析式。同时，结合扭转梁和振动质量的几何尺寸，有限元模态分析和仿真结果表明了主振型是绕弹性扭转梁的扭转振动，符合运动方程的描述。通过设计的静电力驱动电容检测的实验方法，测得的谐振频率为384 Hz，和解析值的相对误差为 5.21%。对解析值，仿真和实验结果的比较发现，它们是接近的和相互能够印证，证明了扭转梁的设计是合理的，也说明刚度系数和固有频率的解析式是正确的，这为今后此种新型陀螺性能的优化提供了理论基础和有效的测试方法。

（

）：

[1] Graney C M. Coriolis effect, two centuries before Coriolis [J]. Physics Today, 2011, 64(8): 8-9.

[2] Liu K, Zhang W P, Chen W Y. The development of microgyroscope technology[J]. Journal of Micromechanics and Microengineering, 2009: 1-29.

[3] Conner P E. MEMS vibratory gyroscopes: structural approaches to improve robustness[M]. Springer, 1979.

[4] Wang W, Lv X, Sun F. Design of a novel MEMS gyroscope array[J]. Sensors, 2013, 13(2): 1651-1663.

[5] 张增平，张福学，高银娟. 旋转载体驱动硅微机械陀螺幅频特性[J]. 中国惯性技术学报，2013，21(2)：245-249.

ZHANG Zeng-ping, ZHANG Fu-xue, GAO Ying-juan Amplitude-frequency characteristics of a silicon micromachined gyro driven by rotating body[J]. Journal of Chinese Inertial Technology, 2013, 21(2): 245-249.

[6] Zhang Zengping, Zhang Fuxue, Zhang Wei. Measurement of phase difference for micromachined gyros driven by rotating aircraft[J]. Sensors, 2013, 13(8): 11051-11068.

[7] Zhang Fuxue, Zhang Zengping, Yan Qingwen, et al. Micro-mechanical pendulum and application technology in the attitude control system of the rotating body[C]// Proceedings of the 2nd International Conference on Electronic and Mechanical Engineering and Information Technology. Shenyang, China, 2012: 119-126 .

[8] Zhang Zengping, Zhang Fuxue, Zhang Wei, et al. The research of vibration suppression method for silicon micro-machined gyro driven by the rotation aircraft[C]// Proceedings of the 2nd International Conference on Electronic and Mechanical Engineering and Information Technology. Shenyang, China, 2012: 80-87.

[9] 张力，林建龙，项辉宇. 模态分析与实验[M]. 北京：清华大学出版社，2011：132.

[10] Yongpeng W, Huilin S. Modeling and simulation for a vibratory tuning-fork MEMS gyroscope[C]//2011 Third International Conference on Measuring Technology and Mechatronics Automation. IEEE, 2011, vol.2: 605-608.

[11] 孙博华，刁方印. 微机械陀螺式加速度器的力学分析[J].暨南大学学报(自然科学与医学版)，2013，34(5)：495-499.

SUN Bo-hua, DIAO Fang-yin. The mechanical analysis of MEMS pendulous oscillating gyroscopic accelerometer[J]. Journal of Jinan University(Natural Science & Medicine Edition), 2013, 34(5): 495-499.

Modal analysis on sensing element of no-driven micromechanical gyro

ZHANG Zeng-ping, ZHANG Fu-xue, ZHANG Wei, LIU Yu, ZHANG Ning
(Sensing Technique Research Center, Beijing Information Science and Technology University, Beijing 100101, China)

The driving structure and detecting structure of traditional micromechanical gyroscope usually require frequency matching, causing narrow bandwidth and complex process. To solve this problem, a novel micromechanical gyroscope was designed, which is mounted on rotating aircraft, obtains angular momentum by using aircraft spin, and senses yawing and pitching angular velocity. Being without driven structure, the gyro’s structure is simple and with large bandwidth. Based on this new structure, the motion equation was established. According to the vibration equation, the torsional beam is the key to vibrating modal and modal frequency of sensing element. Meanwhile, considering the stress, the residual stress’s release and the working ability, the torsional beam was designed to be a circular beam with rectangular cross-section, and the torsional stiffness is analytically derived and calculated to determine the natural frequency. Then the vibrating modal is simulated by using finite element analysis (FEA) method. Simulation results show that the first mode is torsional vibrating, in which the relative error between natural frequency and analytical solution is 9.86%. In order to make further validation, an experimental method using the electrostatic driving and capacitance detection was designed, and the experimental results show that the relative error between natural frequency and analytical solution is 5.21%. Both simulation and experimental results demonstrate that the design is reasonable, and the modal analysis about torsional beam is correct. And it can be applied to the dynamic performance evaluation and the structure optimization.

sensing element; torsional beam; torsion stiffness; natural frequency

联 系 人：张福学（1939—），男，教授，博士生导师。E-mail：zhangfuxue@263.net

1005-6734(2014)05-0655-05

10.13695/j.cnki.12-1222/o3.2014.05.019

U666.1

A

2014-05-02；

2014-08-26

国家自然科学基金委员会资助项目（61372016）；北京市传感器重点实验室开放课题（KF20141077203)；内蒙古自治区自然科学基金项目（2011MS0910）；北京市教育委员会科技计划资助项目（KM201411232021）

张增平（1969—），男，博士研究生，从事微机械惯性器件技术研究。E-mail：zhangzp2007@qq.com