捷联惯性组合误差模型相关性分析方法

刘 璠，魏宗康

（北京航天控制仪器研究所，北京 100039）

捷联惯性组合误差模型相关性分析方法

刘 璠，魏宗康

（北京航天控制仪器研究所，北京 100039）

在实际应用中通过捷联惯性组合误差模型可以将测量值转换成载体导航解算的需要量，而误差模型中的误差系数一般通过标定试验获得。以往认为误差模型中各误差系数相互独立，但通过实际计算可以发现并非如此。为了考量各系数相关性关系，提出了一种相关性分析方法。首先，提出了捷联惯组加速度计输出方程。之后，运用统计学的相关方法计算出了各系数的相关系数和协方差矩阵，并推导出了测量值和误差系数的分布特性之间的关系。最后，通过加速度计组合的实际测试，分别计算了不包含和包含拟合残差的统计数值。通过与输出值进行比对，验证了相关性分析方法的正确性，并表明拟合残差对于统计特性的计算具有重要作用。

捷联惯性测量组合；误差模型；相关性；协方差矩阵

捷联惯性测量组合的测量误差是捷联导航系统的主要误差源之一，对系统的导航精度有很大影响，在导航解算前必须对惯组输出的原始数据进行误差补偿。误差参数主要包括陀螺仪和加速度计的标度因数、零位偏差、安装误差角以及标度因数不对称性误差等，这些参数需要在使用前进行标定，到目前为止已经提出了许多种标定方法[1-5]。因为多种误差的影响，在运用这些标定方法后也无法测出误差系数的精确值，而这也构成了导航误差的一部分，但是由于标定值是在精确值的一定范围内上下波动，所以通过计算多组标定值的统计特性就可以估计出导航系统的导航误差。

在实际应用中，对导航偏差的估计具有重要意义。而与以往认为的各误差系数相互独立不同，实际的计算结果证明误差系数是相关的，所以为了分析输出测量值和误差参数统计特性之间的关系，需要一种参数相关性分析方法。

首先，本文阐述了捷联惯组加速度计输出方程。之后，运用统计学的相关方法计算出了各系数的相关系数和协方差矩阵，并推导出了测量值和误差系数的分布特性之间的关系。最后，通过加速度计组合的实际测试，分别计算了不包含和包含拟合残差的统计数值。通过与输出值进行比对，验证了相关性分析方法的正确性，并表明拟合残差对于统计特性的计算具有重要作用。

1 加速度计输出方程

捷联惯性组合加速度计的输出方程为：

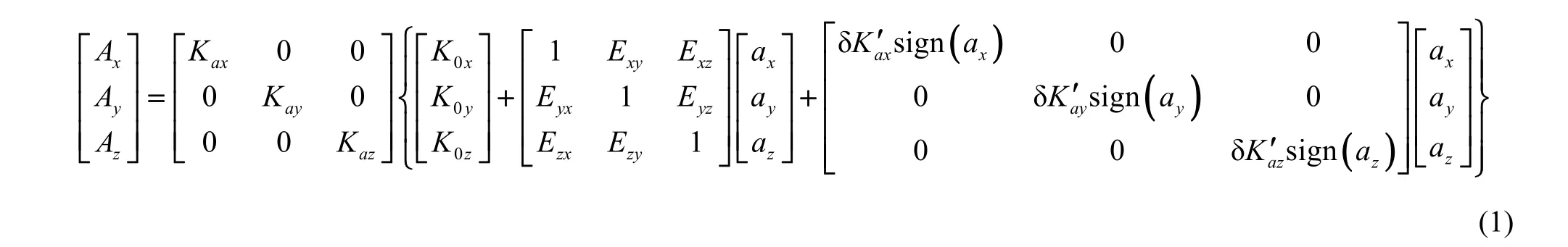
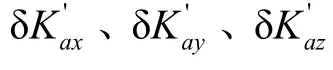
捷联惯性组合加速度计的误差系数一般通过多位置试验进行标定。在进行1组试验后，一般使用最小二乘法进行参数解算。以X轴为例，经过n次测量之后，从式(1)中可以得到：

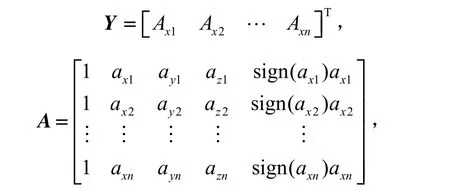
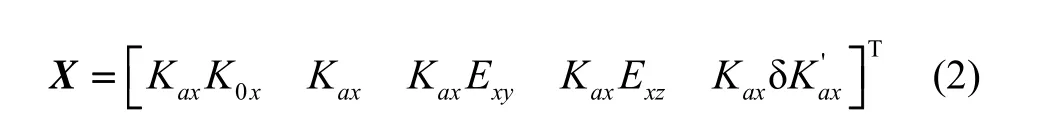
那么，有Y = AX，而通过计算可以得到：

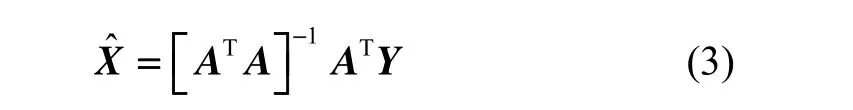
因而得到误差系数的数值。

而如果进行多组测量，在每组中惯组在相同位置的测量值并不完全一样，因此得到的误差系数的解算值也不完全相同。对于每个误差系数，其数值会在一个水平上下波动。在分析输出与输入量统计特性关系时，因为在随机变量分布分析中，两个随机向量的乘积运算复杂，难以求得结果。为了避免这点，设：

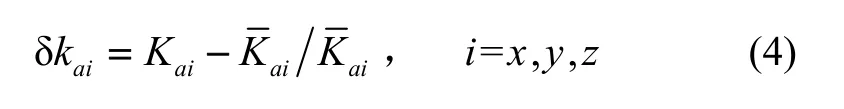
式中， Kai为每组测量后解算得到的标度因数，为标度因数的解算平均值。忽略二阶小量并且考虑拟合残差后，加速度计组合的输出方程可表示为：

一般认为，各误差系数之间相互独立，因此以X轴为例，在一个位置上，输入输出量拥有统计关系：

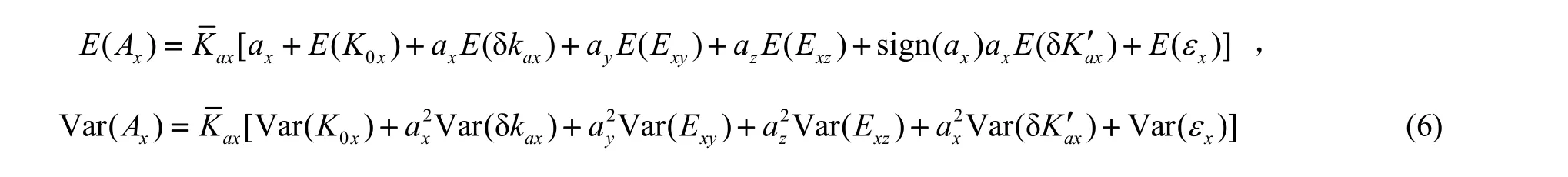
但是，在实际计算中可以发现，式(6)中的方差部分不成立，这是因为物理上的相互联系导致各误差系数并不相互独立。当使用误差系数的统计分布推算输出量的分布特性时，需要分析各误差系数的相关性。

2 协方差矩阵和系数相关性

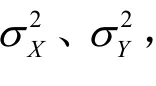
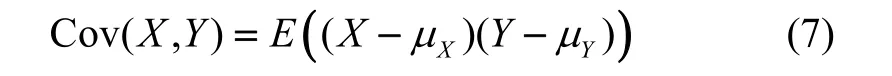
而

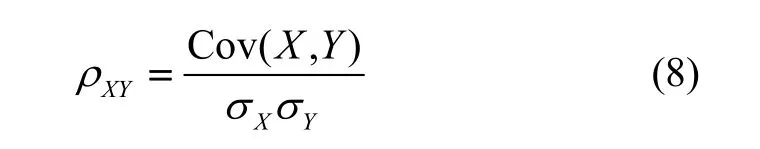
称为X和Y的相关系数。

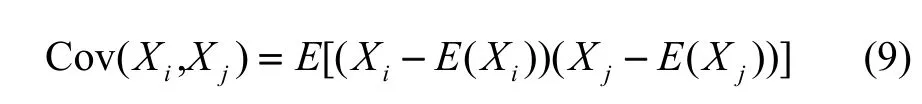
设系统输出方程为：

式中，y为系统输出，也为测量值；A为系统各输入变量组成的向量，为1× m维；X为系统各输入量对应的系数值，为 m×1维；ε为计算残差。

经过n组测量后，每组测量后拟合得到的系数值为 X1,…,Xn，在每组中选出拥有同样输入向量 A的测量值 y1，…， yn，每个测量值对应的解算残差分别为 ε1,…,εn，则有：

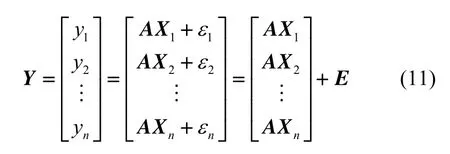
其平均值有关系式：

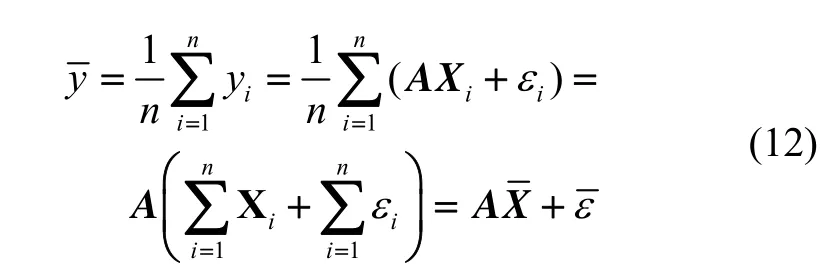
定义测量输出Y的方差为：

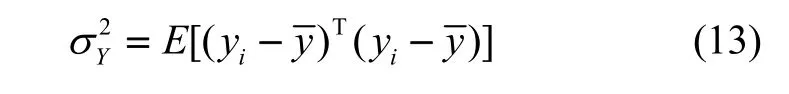
定义拟合残差E的方差为：

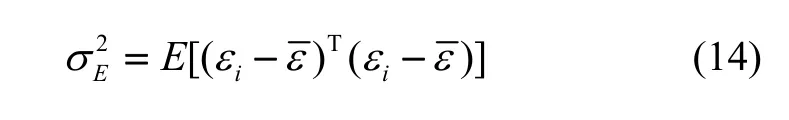
定义X的协方差矩阵为Σ，则有：

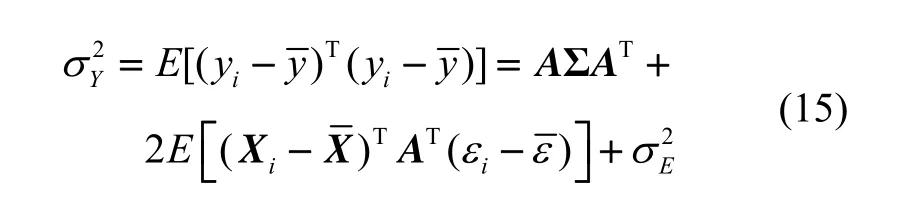
从上式可以看出，输出 Y的方差除与各项系数的方差有关外，还与拟合残差的方差有关。如果拟合残差的影响较小，则有近似关系：

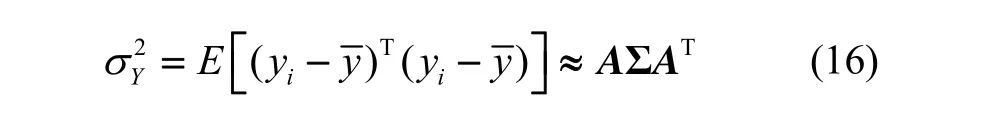
3 加速度计组合分析实例

3.1 加速度计输出统计特性

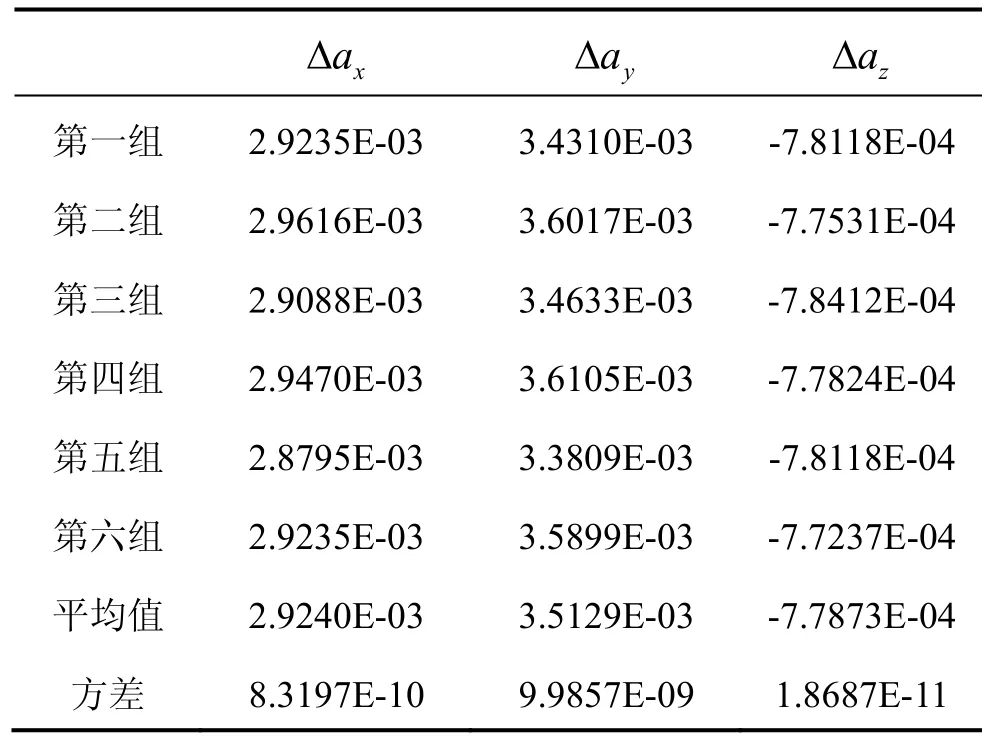
表1 加速度计组合6次计算值Tab.1 6 calibration results of accelerometers

3.2 不考虑拟合残差时拟合值统计特性

按照式(5)，不考虑拟合残差时，加速度计组合X轴的误差模型可写为：

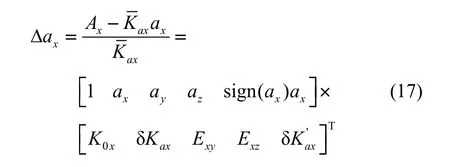
对于上式中的各误差参数，代入标定结果，得到相关系数如表2所示。

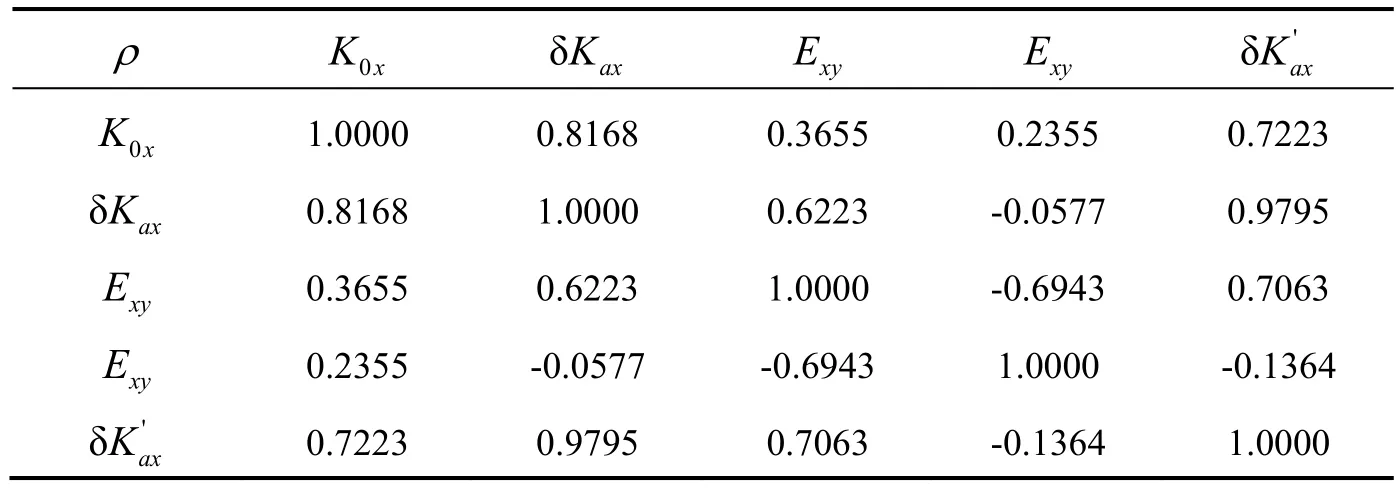
表2 X轴各参数之间相关系数计算结果Tab2. The correlation of parameters in the X axis

按照式(10)对应式(17)，显然有：

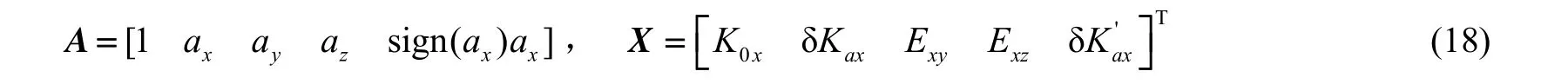
那么，

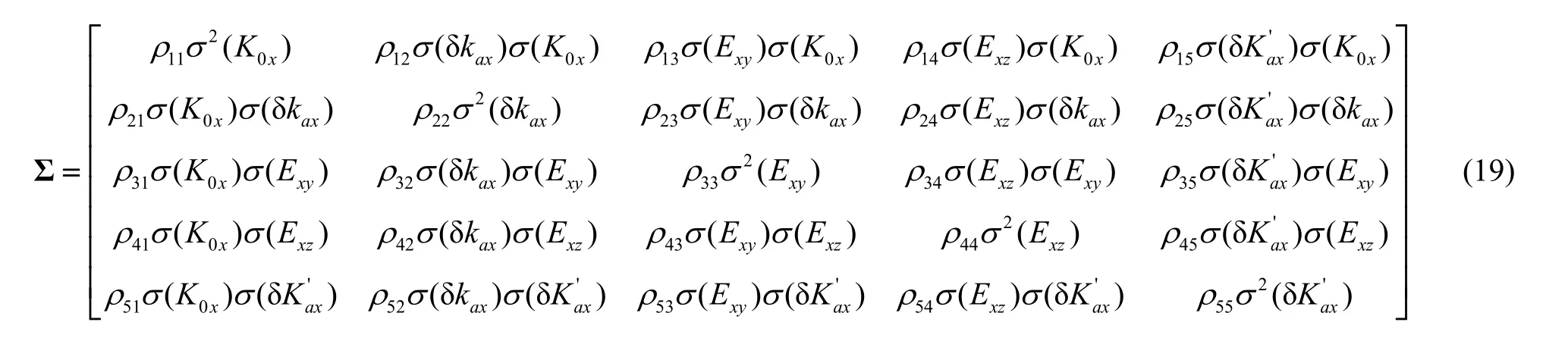
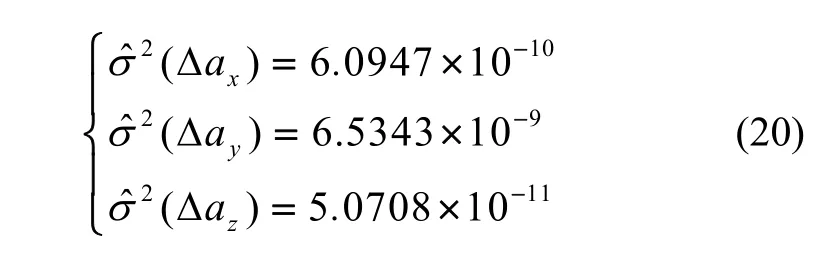
此外，加速度计组合的拟合输出平均值为：

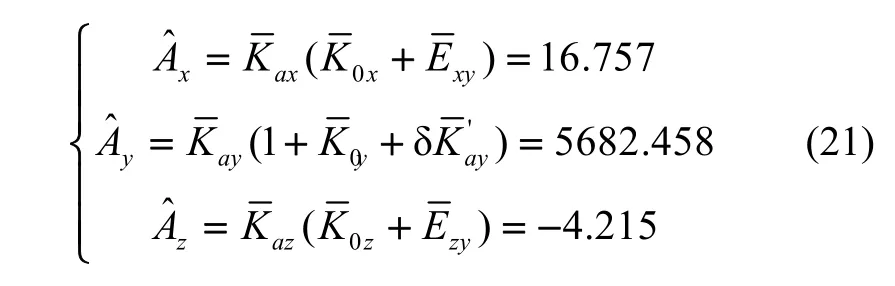
显然，这一计算结果与实际测试值并不相符，且相差较大。因此，需要考量拟合残差的影响。

3.3 考虑拟合残差时拟合值统计特性

当考虑拟合残差时，加速度计的误差模型可写为：

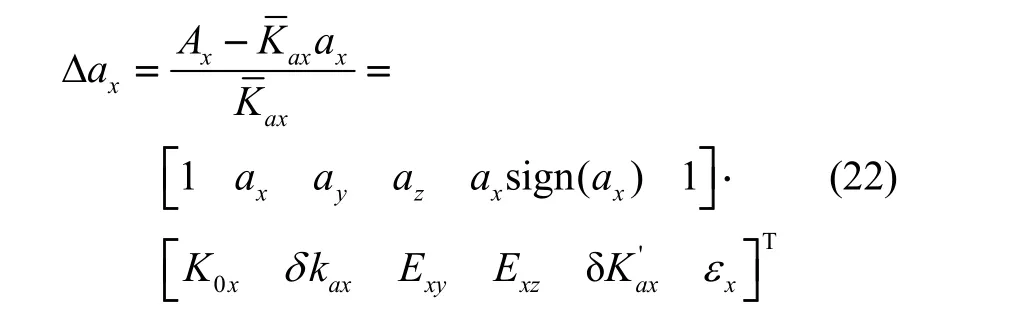
对于增加了拟合残差后的各误差参数，其相关系数如表3所示。

此时有新的向量A和X为：

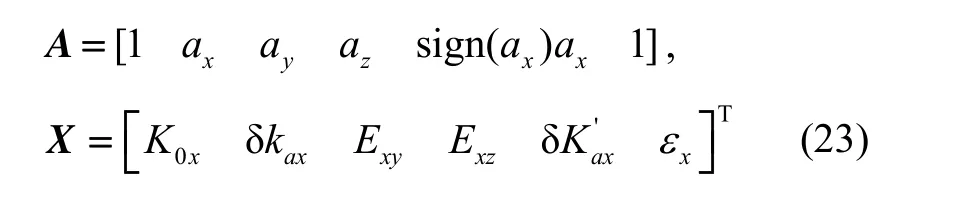
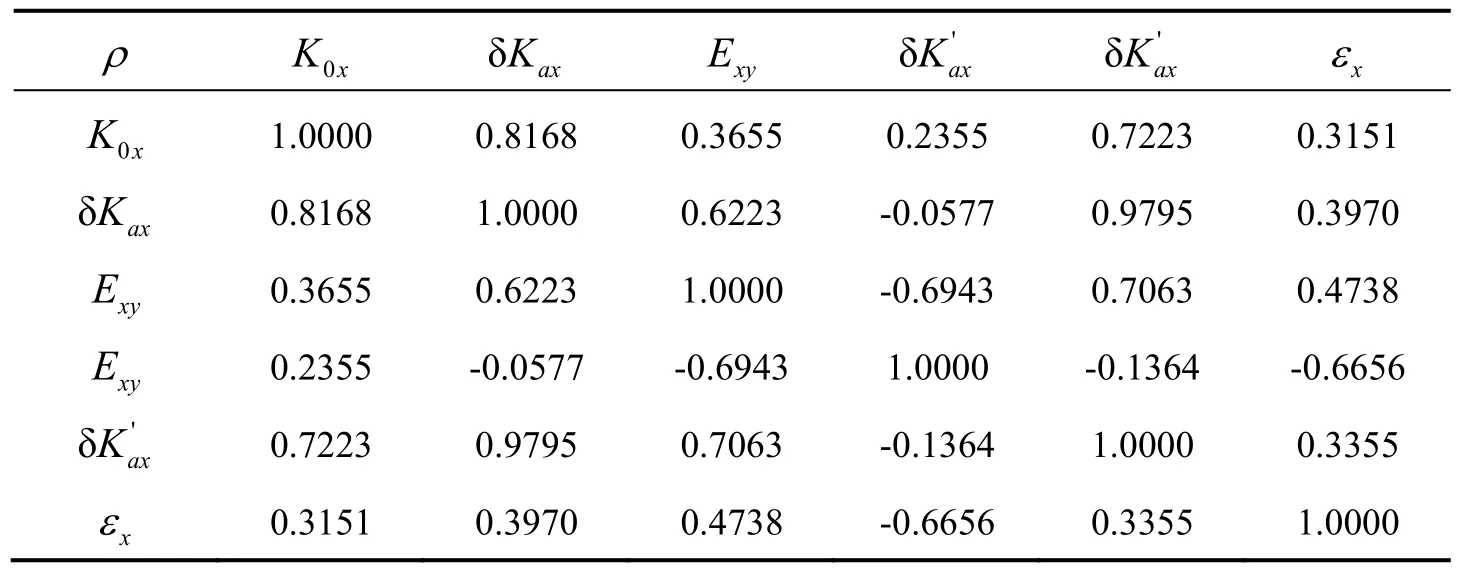
表3 X轴各参数之间相关系数计算结果Tab.3 The correlation of parameters in the X axis

新的向量X的协方差矩阵为：

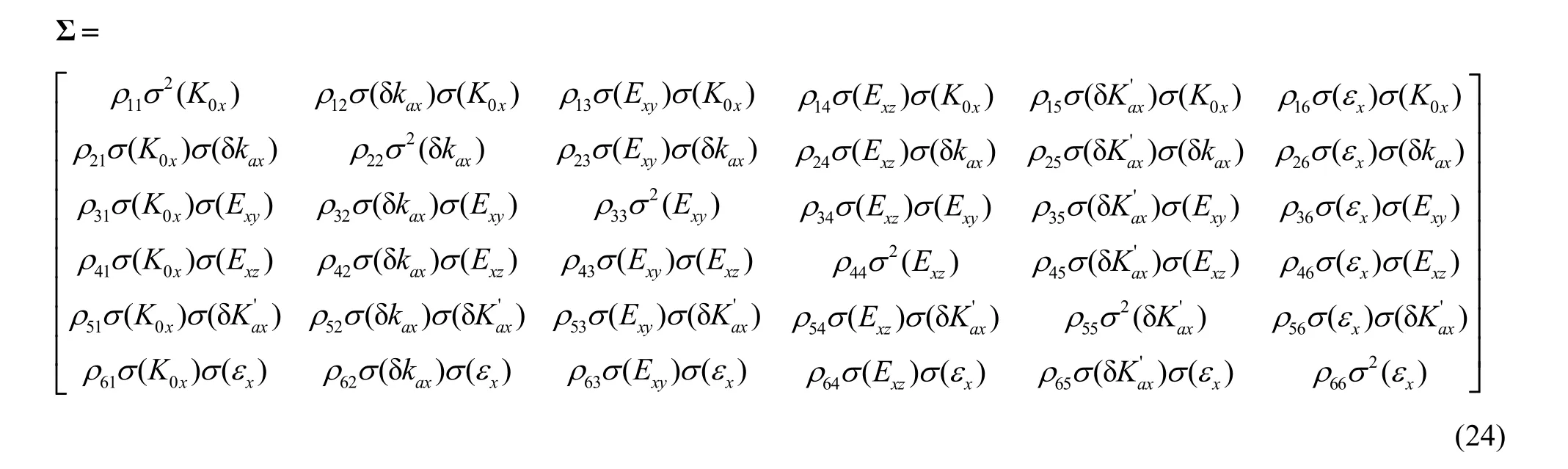
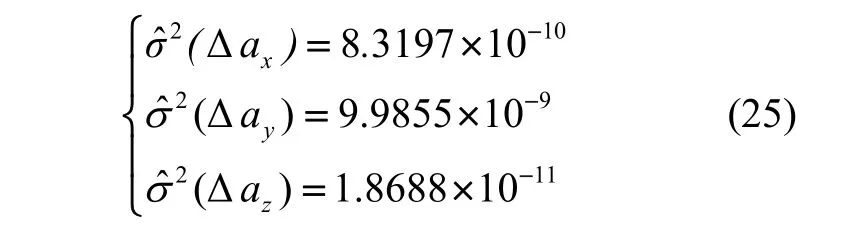
三个轴向加速度计输出的平均值为：

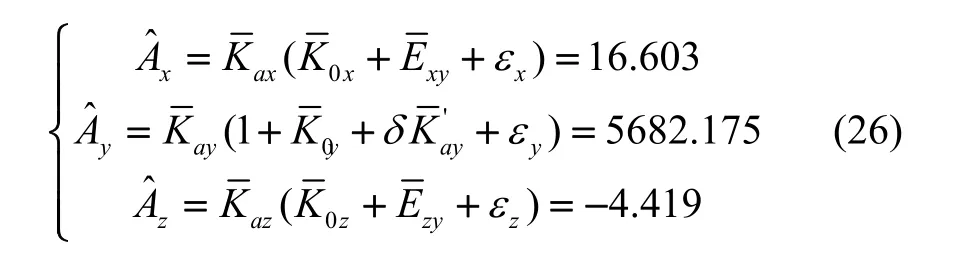
比较三轴加速度计平均值、方差的计算结果与实际测试数值，可以看出二者相等。显然，拟合残差的分布特性会影响加速度计输出的统计计算，如果不考虑的话，结果将有较大的偏差。

4 结 论

在本文中，首先引入了统计学中随机向量协方差矩阵的计算方法。然后，推导了随机向量的线性函数中，自变量和因变量之间平均值和方差之间的关系。之后，以捷联惯性组合加速度计的输出方程为例，利用实际标定数据结果，对加速度计输出量和输入量以及拟合残差的相关性进行了分析。

最终结果表明，在输出量的分析中，需要考虑拟合残差的影响，否则将有较大的偏差。应用本文提供的方法可以有效判定实际使用时惯组加速度的置信范围，为确定导航精度提供了可靠的数据基础。

（

）

[1] Cho S Y, Park C G A. Calibration technique for a redundant IMU containing low-grade inertial sensors[J]. ETRI Journal, 2005, 27(4): 418-426.

[2] 谢波，秦永元，万彦辉. 激光陀螺捷联惯导系统多位置标定方法[J]. 中国惯性技术学报，2011，19(2)：157-162，169.

XIE Bo, QIN Yong-yuan, WAN Yan-hui. Multiposition calibration method of laser gyro SINS[J]. Journal of Chinese Inertial Technology, 2011, 19(2): 157-162, 169.

[3] 林红斌，解静，王妍. 基于正弦直线过载的惯组动态误差标定方法[J]. 系统工程与电子技术，2013，35(10)：2152-2157.

LIN Hong-bin, XIE Jing, WANG Yan. Calibration method for IMU dynamic error based on sinusoidal linear acceleration[J]. Systems Engineering and Electronics, 2013, 35(10): 2152-2157.

[4] 杨晓霞，孟浩然，王帅. 激光陀螺捷联惯导系统的外场动态标定方法[J]. 中国惯性技术学报，2011，19(4)：393-398.

YANG Xiao-xia, MENG Hao-ran, WANG Shuai. Calibration method for laser gyro SINS under outer field dynamic conditions[J]. Journal of Chinese Inertial Technology, 2011, 19(4): 393-398.

[5] 薛文超，牟玉涛，黄一等. 外场条件下激光捷联惯组多位置标定方法精度分析[J]. 中国惯性技术学报，2012，20(1)：39-45.

XUE Wen-chao, MOU Yu-tao, HUANG Yi, et al. Precision analysis for laser SINS’s calibration in outer field[J]. Journal of Chinese Inertial Technology, 2012, 20(1): 39-45.

[6] 范俊花，林金官，韦博成. 具有一致相关的纵向数据模型中方差和相关系数的齐性检验[J]. 应用概率统计，2009，25(1)：12-26.

FAN Jun-hua, LIN Jin-guan, WEI Bo-cheng. Testing for homogeneity of variance and correlation coefficients in uniform correlation models based on longitudinal data[J]. Chinese Journal of Applied Probability and Statistics, 2009, 25(1): 12-26.

[7] Zhang F, Weiss R E, Diagnosing explainable heterogeneity of variance in random-effects models[J]. Canad. J. Statust, 2000, 28: 3-18.

[8] Lan C, Giambelluca T W, et al. Lumped parameter sensitivity analysis of a distributed hydrological model within tropical and temperate catchments[J]. Hydrological Processes, 2011, 25(15): 2405-2421.

[9] Babichenko A V, Shkred V K. Main errors of inertial navigation systems[J]. Engineering Physics, 2011, 11(3)：34-53.

[10] Batista P, Silvestre C, Oliveira P, et al. Accelerometer calibration and dynamic bias and gravity estimation: analysis, design, and experimental evaluation[J]. IEEE Trans. on Control Systems Technology, 2011, 19(5): 1128-1137.

Correlation analysis method for error model of strapdown IMU

LIU Fan, WEI Zong-kang
(Beijing Aerospace Control Device Institute, Beijing 100039, China)

By using the error model of strapdown inertial measurement unit (SIMU), the measurements can be translated into the needed variable, and the error coefficients in the error model are usually obtained by calibration tests. In the past, the parameters were thought to be statistically independent, but it is proved wrong by our calculation. In this paper, a method for analyzing the correlation of parameters is studied. Firstly, the error model of the accelerometer of IMU is given. Then the matrix of covariance and correlation of parameters are calculated out with the knowledge of statistical method. The distribution relation between the measurements and error parameters is deducted. At last, with a real test of IMU accelerometers, the statistic values with and without fitting residues are computed, respectively. The method is proved to be valid by comparing with the statistic value of measurements, and the fitting residues are shown to play an important ro le in the calculation of statistical properties.

strapdown inertial measurement unit; error model; correlation; covariance matrix

1005-6734(2014)05-0567-05

10.13695/j.cnki.12-1222/o3.2014.05.002

U666.1

A

2014-05-14；

2014-08-21

民用航天专业技术预先研究项目（D010101）；国防基础科研项目（B030080021）

刘璠（1987—），男，工程师，从事导航、制导与控制专业研究。 E-mail：finelf@sina.com