基于单向无迹卡尔曼滤波的飞机姿态算法

韩 萍，桑威林，赵爱军，Daniel Alazard

（1. 中国民航大学 智能信号与图像处理天津市重点实验室，天津 300300；2. 东方通用航空有限责任公司，天津 300300；3. 法国国立航空航天大学 数学与控制系，图卢兹 31555，法国）

基于单向无迹卡尔曼滤波的飞机姿态算法

韩 萍1，桑威林1，赵爱军2，Daniel Alazard3

（1. 中国民航大学 智能信号与图像处理天津市重点实验室，天津 300300；2. 东方通用航空有限责任公司，天津 300300；3. 法国国立航空航天大学 数学与控制系，图卢兹 31555，法国）

针对扩展卡尔曼滤波方法在飞机姿态滤波中存在的线性化误差大、需要解繁琐的Jacobian矩阵等问题，将一种新型卡尔曼滤波方法——单向无迹卡尔曼滤波应用于载有低精度、高噪声传感器的低成本飞机姿态滤波系统，并在精度及计算量上与EKF和容积卡尔曼滤波进行了比较。利用实测飞行数据进行实验，结果表明：相对于EKF，SUKF实现容易，且使姿态滤波精度提高到二阶；相对于CKF，SUKF计算简单，比CKF减少约33%的计算量。

姿态滤波；单向无迹卡尔曼滤波；扩展卡尔曼滤波；容积卡尔曼滤波；计算量

扩展卡尔曼滤波（Extended Kalman Filter, EKF）是飞机姿态滤波中的常用方法，该方法将非线性函数Taylor展开式的一阶项作为非线性函数的近似，从而将非线性问题转换为线性问题进行处理[1-5]。但对于精度低、噪声大的传感器，EKF自身存在的线性化误差被加大，只能保证一阶精度；另外EKF需要求解繁琐的Jacobian矩阵，使得其计算相对复杂。

最近由常路宾等提出了一种新型卡尔曼滤波——单向无迹卡尔曼滤波（Simplex Unscented Kalman Filter, SUKF）[6]，该方法根据“近似非线性函数的概率分布比近似非线性函数更容易”的思想，并结合数学理论“对于n维的状态矢量，只需要 n+1个合适的点就可以完全表征其均值和方差”，通过构造 n+1个等权重的采样点进行状态估计，使估计提高到二阶精度。

本文将SUKF应用于飞机姿态滤波，利用从微型实验飞机上获取的飞行数据进行实验，并将实验结果与EKF和CKF[7]得到的结果进行比较。实验表明，在传感器精度低，数据噪声大的情况下，SUKF有效地提高了滤波精度、运算效率和实时性，减少了计算量。

1 单向无迹卡尔曼滤波

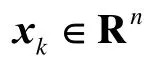
SUKF是一种确定采样型滤波方法，它采取了构造单向采样点的方式来达到逼近状态后验分布的目的，采样点的具体构造过程如下[6]：

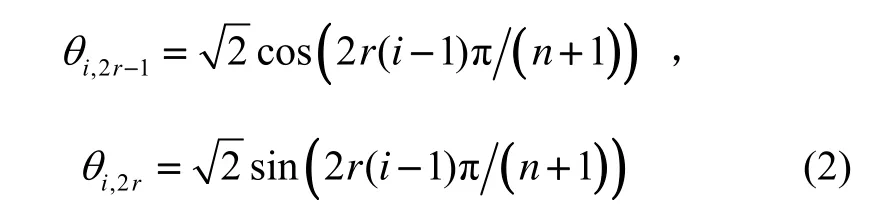
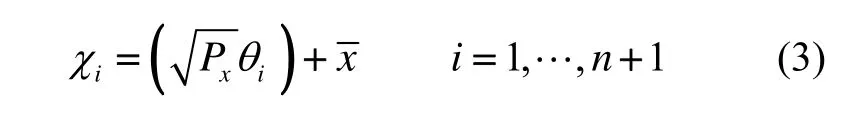
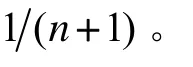
SUKF的具体实现过程如下：

1）时间更新

① 确定时间更新采样点

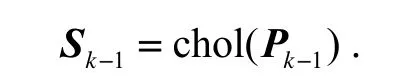
chol(·)表示对矩阵进行Cholesky分解：

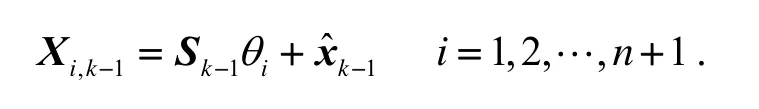
2）量测更新

③ 计算卡尔曼增益

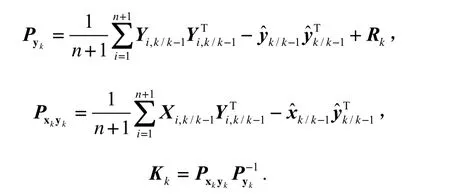
④ 状态变量更新

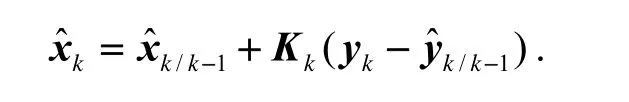
⑤ 误差协方差更新

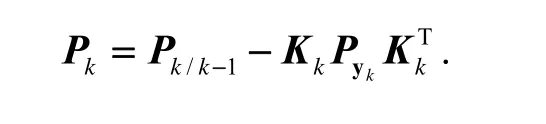
2 飞机姿态滤波系统模型

2.1 姿态解算方程

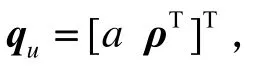
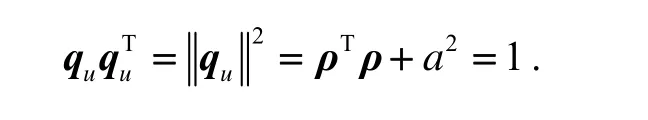
由刚体转动理论，得姿态四元数运动方程为：

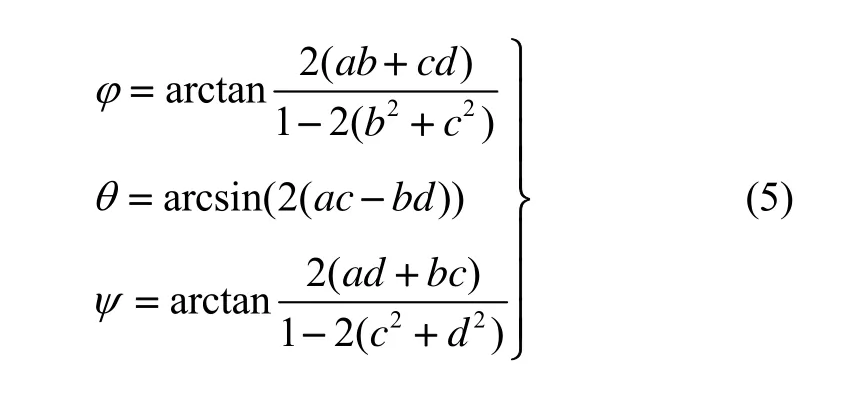
2.2 系统状态方程

本文用四元数来描述飞机姿态，姿态解算时需要角速度。此外为了提高姿态滤波精度，用陀螺仪的随机游走在线补偿陀螺仪测量误差，所以状态矢量定为四元数、角速度和陀螺仪随机游走的组合，即系统状态矢量为：

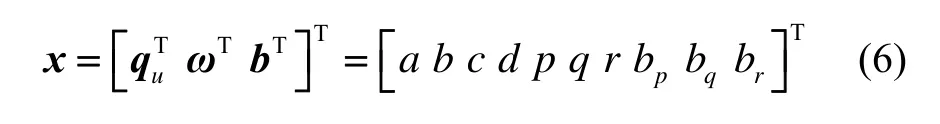
陀螺仪广泛采用的模型为[12]：

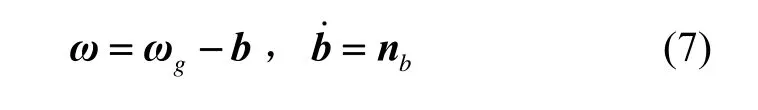
四元数与角速度的关系如图1所示。

图1 角速度和四元数处理模型Fig.1 Process model for angular rates and quaternion

由此建立飞机姿态滤波系统的非线性状态方程如下[13]：

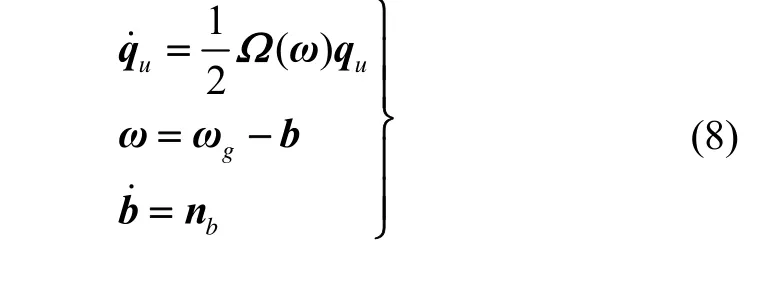
2.3 系统观测方程

本实验所用姿态传感器由三轴加速度计、三轴磁强计和三轴陀螺仪组成，由它们获得飞机机体坐标系下的重力矢量、磁场矢量和转动角速度，将这些参量作为观测矢量，即：

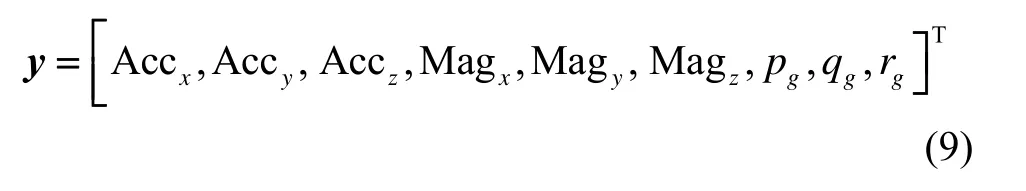
根据捷联惯性导航基本原理，利用姿态矩阵将导航坐标系矢量转换成机体坐标系矢量。由此建立系统观测方程如下[13]：

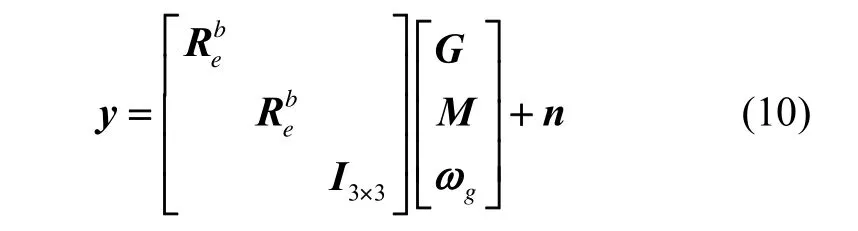
式中，

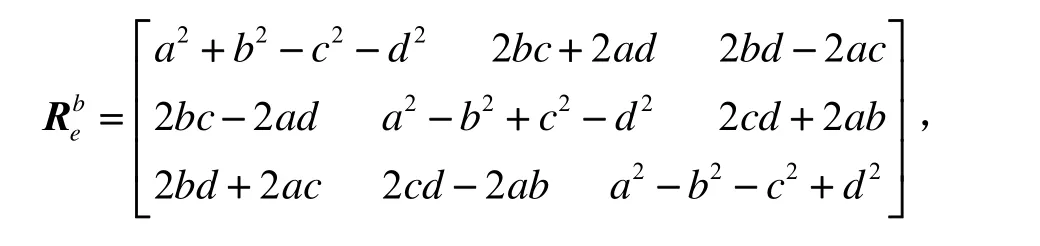
3 实验结果与分析

本文实验数据采自于装有美国CH Robotics公司生产的CHR-6dm传感器和法国SBG Systems公司生产的SBG传感器的微型实验飞机。两种传感器均含有正交的三轴陀螺仪、三轴加速度计和三轴磁强计，并可提供未经处理的机体坐标系下三个方向的角速度、重力矢量和地磁场矢量。利用加速度计和磁强计对地球重力场和地磁场的测量值补偿陀螺仪漂移，可以提高系统滤波精度，增强系统稳定性。两种传感器内部集成的均是EKF滤波方法，由于制作工艺不同，SBG传感器精度比CHR-6dm传感器精度要高，但价格也要高很多，约为CHR-6dm传感器7倍。为了验证SUKF在高噪声、低精度数据源时姿态滤波的有效性，将高精度SBG传感器输出的姿态角作为基准，CHR-6dm传感器获得的数据作为源信号进行处理。

实验中，两个传感器采样频率均为100 Hz，状态矢量初值设为：

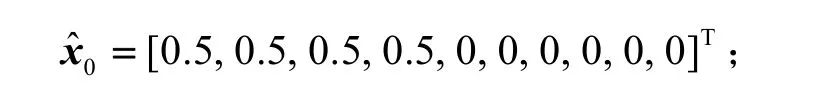
实验初始阶段飞机处于地面启动状态，利用此时段采集的数据计算过程噪声协方差矩阵Q和观测噪声协方差矩阵R。实验结果如图2～4所示。

为便于比较，将EKF和CKF滤波误差也置于图2～4中。由图可知，SUKF滤波误差小于EKF，较CKF也有改善，波动性小于EKF，且容易达到稳定，是一种有效的姿态滤波方法。

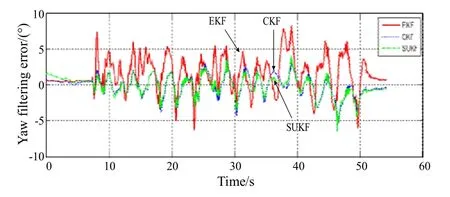
图2 航向角滤波误差Fig.2 Yaw filtering error

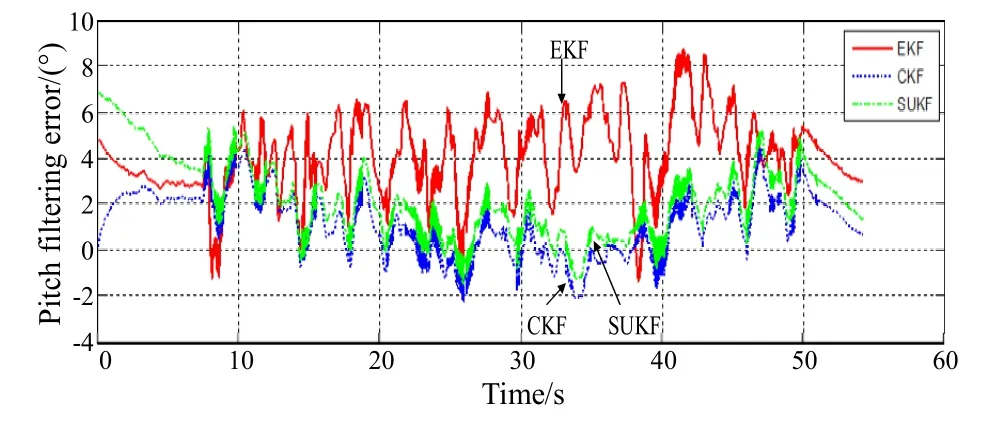
图3 俯仰角滤波误差Fig.3 Pitch filtering error

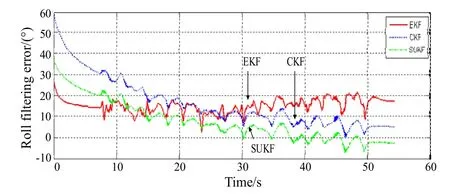
图4 滚转角滤波误差Fig.4 Roll filtering error

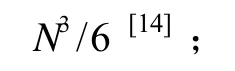
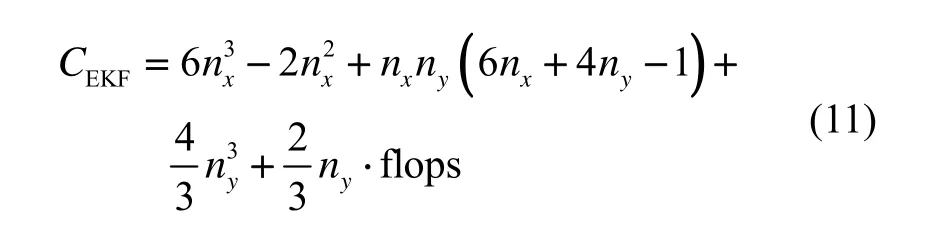
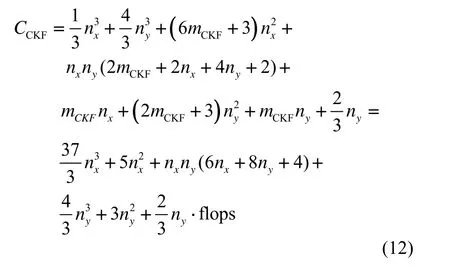
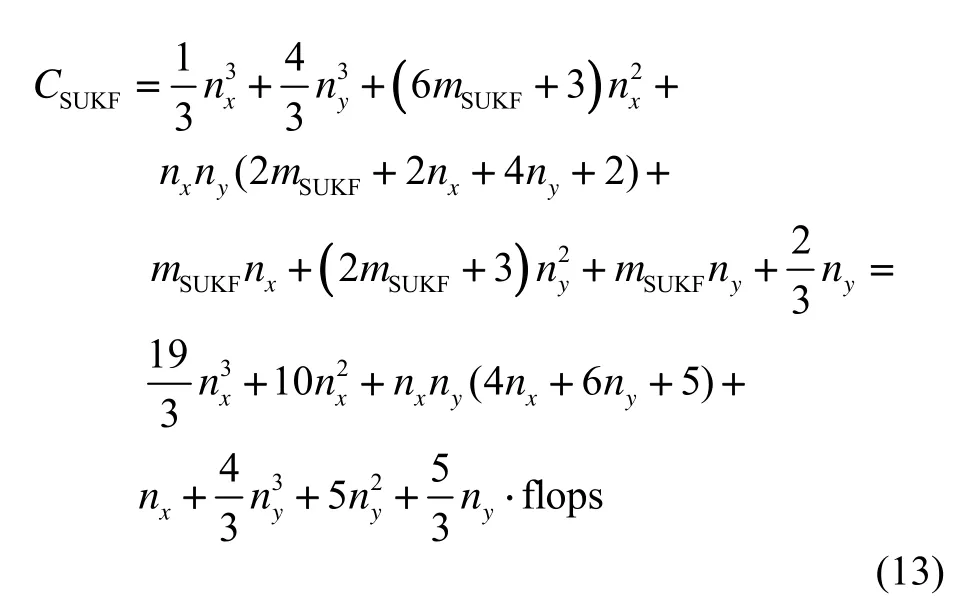
由式(12)(13)可得CKF与SUKF的运算量差值 Cdif为：

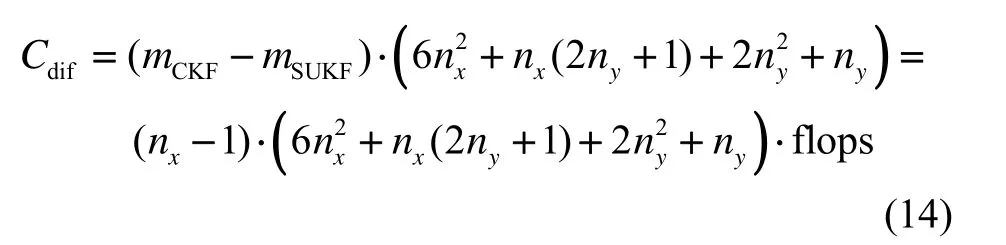
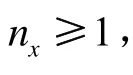
由表1知，CKF/EKF约为1.69，SUKF/EKF约为1.14；在保证二阶精度的情况下，SUKF比CKF少约32.89%的计算量，与EKF计算量基本相当。

表1 EKF、CKF与SUKF运算量Tab.1 Computational Cost of EKF, CKF and SUKF

4 结 论

本文将单向无迹卡尔曼滤波应用于由低精度高噪声传感器组成的低成本飞机姿态滤波系统，利用多组实测数据进行验证，并给出了各方法计算量的统计对比。实验表明：相对于EKF，SUKF在姿态滤波过程中无需求导计算繁琐的Jacobian矩阵，实现容易，且使滤波精度得到提高。相对于CKF，SUKF有效地提高了运算效率和实时性，是一种高效的姿态滤波方法。

（

）：

[1] 付梦印，邓志红，张继伟. Kalman滤波理论及其在导航系统中的应用[M]. 北京：科学出版社，2003：82-84.

FU Meng-yin, DENG Zhi-hong, ZHANG Ji-wei. Kalman filtering theory and its application in navigation system [M]. Beijing: Science Press, 2003: 82-84.

[2] 王小旭，潘泉，黄鹤，等. 非线性系统确定采样型滤波算法综述[J]. 控制与决策，2012，27(6)：801-812.

WANG Xiao-xu, PAN Quan, HUANG He, et al. Overview of deterministic sampling filtering algorithms for nonlinear system[J]. Control and Decision, 2012, 27(6): 801-812.

[3] XU Yuan, CHEN Xi-yuan, LI Qing-hua. Unbiased tightlycoupled INS/WSN integrated navigation based on extended Kalman filter[J]. Journal of Chinese Inertial Technology, 2012, 20(3): 292-295.

[4] 郝燕玲，杨峻巍，陈亮，等. 基于平方根中心差分卡尔曼滤波的大方位失准角初始对准[J]. 中国惯性技术学报，2011，19(2)：180-189.

HAO Yan-ling, YANG Jun-wei, CHEN Liang, et al. Initial alignment of large azimuth misalignment based on square root central difference Kalman filter[J]. Journal of Chinese Inertial Technology, 2011, 19(2): 180-189.

[5] 黄耀光，高博，李建新，等. 基于平方根UKF双向滤波的单站无源定位算法[J]. 数据采集与处理，2013，28(2)：207-212.

HUANG Yao-guang, GAO bo, LI Jian-xin, et al. Singleobserver passive location algorithm based on square-root UKF with forward-backward filtering[J]. Journal of Data Acquisition & Processing, 2013, 28(2): 207-212.

[6] HU B Q, Chang L B, Li A, et al. Computationally efficient simplex unscented Kalman filter based on numerical integration[J]. Asian Journal of Control, 2014, 16(2): 1-7.

[7] Arasaratnam I, Haykin S. Cubature Kalman filters[J]. IEEE Transaction on Automatic Control, 2009, 54(6): 1254-1269.

[8] LIU Hua, LIU Tong. Quaternion based constrained algorithm in federated Kalman filtering for MEMS IMU/GNSS[J]. Journal of Chinese Inertial Technology, 2013, 21(3): 392-396.

[9] 高社生，李伟，桑春萌. 基于四元数的SINS/SAR组合导航系统[J]. 中国惯性技术学报，2010，18(1)：63-69.

GAO She-sheng, LI Wei, SANG Chun-meng. SINS/SAR Integrated navigation system using quaternion model [J]. Journal of Chinese Inertial Technology, 2010, 18(1): 63-69.

[10] 乔相伟，周卫东，吉宇人. 用四元数状态切换无迹卡尔曼滤波器估计的飞行器姿态[J]. 控制理论与应用，2012，29(1)：97-103.

QIAO Xiang-wei, ZHOU Wei-dong, JI Yu-ren. Aircraft attitude estimation based on quaternion state-switching unscented Kalman filter[J]. Control Theory & Applications, 2012, 29(1): 97-103.

[11] Choi M H, Porter R, Shirinzadeh B. Comparison of attitude determination methodologies with low cost inertial measurement unit for autonomous aerial vehicle [C]//IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Wollongong, Australia, 2013: 1349-1354.

[12] Karlgaard C D, Schaub H. Adaptive huber-based filtering using projection statistics: Application to spacecraft attitude estimation[C]//AIAA, Guidance, Navigation, and Control Conference, Honolulu, USA, 2008: 1-20.

[13] Han Ping, Gan Haoliang, He Weikun, et al. Aircraft attitude estimation based on central difference Kalman filter[C]// Proceedings of 2012 IEEE the 11th International Conference on Signal Processing. Beijing, China, 2012: 294-298.

[14] Press W H, Teukolsky S A, Vetterling W T, Flannery B P. Numerical recipes in C: The art of scientific computing [M]. 2nd Edition. New York, Cambridge University Press, 1997: 96-98.

[15] Chapra S C, Canale R P. Numerical methods for engineers [M]. 6th Edition. New York: Mc Graw Hill Higher Education, 2010: 283-286.

Simplex unscented Kalman filter for aircraft attitude algorithm

HAN Ping1, SANG Wei-lin1, ZHAO Ai-jun2, Daniel Alazard3
(1. Tianjin Key Lab for Advanced Signal Processing, Civil Aviation University of China, Tianjin 300300, China; 2. Eastern General Aviation CO.LTD, Tianjin 300300, China; 3. Department of Mathematics and Control, Institut Supérieur de l'Aéronautique et de l'Espace, Toulouse 31555, France)

In view that the Extended Kalman Filter(EKF) in aircraft’s attitude filtering has such problems as large linearization error and having to solve complex Jacobian matrix, etc., a new Kalman filter algorithm named Simplex Unscented Kalman Filter(SUKF) is applied into a low-cost aircraft attitude filtering system equipped with less accurate and high noisy sensors. Meanwhile, a comparison on accuracy and calculation cost among EKF, Cubature Kalman filter(CKF) and SUKF is conducted. Experimental results with real flying data show that the SUKF is easy to implement and increases the attitude filtering accuracy to the second order with respect to EKF. Moreover, the SUKF is simple in computation, and the computational cost decreases about 33% compared with that of CKF.

attitude filtering; simplex unscented Kalman filter; extended Kalman filter; cubature Kalman filter; computational cost

1005-6734(2014)05-0629-05

10.13695/j.cnki.12-1222/o3.2014.05.014

V249.32

A

2014-05-09；

2014-09-02

国家自然科学基金（61231017）；中央高校基金（ZXH2012D001）

韩萍（1966—），女，博士，教授，从事数字信号处理与模式识别研究。E-mail：hanpingcauc@163.com