基于Choquet模糊积分的边坡稳定性评价

王兴霞，黄 琴，廖再毅,2

（1.三峡大学水利与环境学院，湖北 宜昌 443002；2.瑞尔森大学建筑系，加拿大 多伦多 M5B 2K3）

0 引 言

工程建设过程中产生的大量高陡边坡给经济的发展和人民的生命财产带了巨大的威胁。如何对边坡的稳定性进行有效的评价与分析具有重要的实用和经济意义[1]。针对各类工程中的边坡稳定性分析问题，国内外专家学者做了大量的研究工作，在传统的方法基础上提出了一些有效的边坡稳定性评价方法，这些方法都有各自的优点和适用性，但也存在着一定的缺陷和局限性，如灰色聚类法、模糊层次法、神经网络法、可靠度法、基于粗糙集理论法、基于可拓学理论法等[2-8]。通常认为，边坡稳定性评价指标之间是相互独立、互不影响、互不交叉的。但是，在现实问题中，影响边坡稳定性的诸多属性指标往往是相互依赖、相互联系的，并不相互独立。鉴于此，为尽可能避免评价失真，使评价结果更加科学合理，本文将模糊测度和Choquet积分算子[9-10]引入到边坡稳定性评价中，建立基于Choquet模糊积分的评价模型，对边坡的稳定性进行评价。

1 评价模型

针对评价指标互相关联、不具可加性的特点，日本学者Sugeno于1974年提出了模糊测度的概念[9]，然而Sugeno积分并不能使测度满足可加性。为避免这一缺陷，Murofushi和Sugeno提出了Choquet模糊积分[10]，并将其应用到基于关联的决策分析中。本文考虑评价因素之间的关联性，建立基于Choquet模糊积分的评价模型。

1.1 模糊测度

设X= （x1，x2，…，xn）为非空集合，μ是X上的模糊测度。在实际评价过程中，X一般定义为评价指标集，通常是有限的，对任意的指标集S⊆X，μ(S)为评价指标集S的重要程度或权重。因此，模糊测度除了可度量每个评价指标的重要程度或权重，还可以定义任意属性指标集的权重。

对任意的A，B∈P(X)，A∩B=Ø。如果模糊测度μ满足以下条件

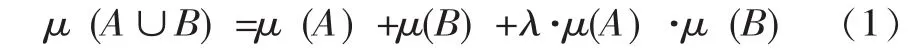
则称μ(A)，μ(B)分别为关于集合A，B的λ模糊测度，该模糊测度是带参数λ的一种重要的模糊测度，λ∈ （-1，∞），当λ≥0时，λ模糊测度为信任模糊测度。

对于单个评价指标xi∈X，μ(xi)称为xi的模糊密度函数，表示属性xi的重要程度，根据下式可确定唯一的参数λ

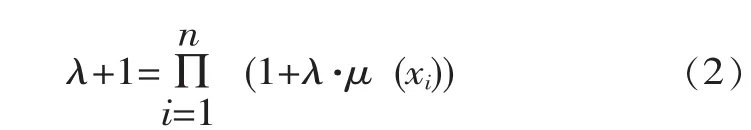
1.2 Choquet模糊积分

模糊积分作为一种定义在模糊测度基础上的非线性函数，通过模糊测度来衡量多指标的重要程度[11]，不需要假设各评价指标间是相互独立的，只要符合单调性即可使用，被应用于评价指标之间存在相互关联的情况，操作比较方便[12]。模糊积分的方式有很多，其中Choquet模糊积分应用最为广泛，利用模糊测度，通过评价指标各自重要程度来描述评价指标间相互作用的程度。

假设X={x1，x2，…，xn}是一个非空集合，f是定义在X上的非负实值函数，f:X→R+，函数f关于μ的Choquet模糊积分定义为

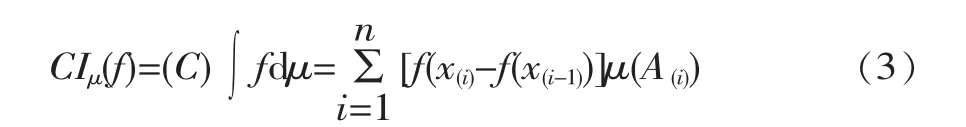
式中，(·)表示函数f在X上的一个转置，使得f(x(1))≤f(x(2))≤…≤f(x(n))且 A(i)≤{x(i)，…，x(n)}，x(0)=0。

由上可知，Choquet模糊积分的特点是对数据（f(x1)，f(x2)，…，f(xn)，）按从小到大或从大到小的顺序重新排序后的线性表示，考虑了实际评价中各评价指标及指标集之间普遍存在的相互关联和影响的现象，这种排序方法决定了不同评价指标集的重要程度。

1.3 评价步骤

假设E={e1，e2，…，er}为专家集，X={x1，x2，…，xn}为评价指标集，S={s1，s2，…，sl}为评价标度集。运用Choquet模糊积分[12-13]，提出基于Choquet模糊积分的边坡稳定性评价方法，具体步骤如下。

步骤1:假定第k位专家根据具体边坡的实际情况，以评价标度集S为依据，对待评边坡的第j（j=1，2，…，n）个评价指标xj进行评价测度，得到评价指标xj的评价值为rkj(rkj∈S)，得到第k位专家的评价向量为

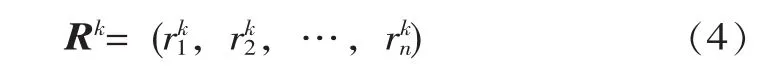
步骤2:确定集合X中评价指标xj的模糊密度μ(xj)(j=1，2，…，n)，μ(xj)可利用层次分析法或Delphi法确定，根据公式 （2）确定其相应的参数λ1。

步骤3:确定集合E中专家ek的模糊密度μ(ek)(k=1，2，…，r)，根据公式 （2）确定其相应的参数λ2。

步骤4:利用Choquet模糊积分对评价向量Rk的评价信息进行集结，得到专家ek对待评边坡的综合评价值rk(k=1，2，…，r)为

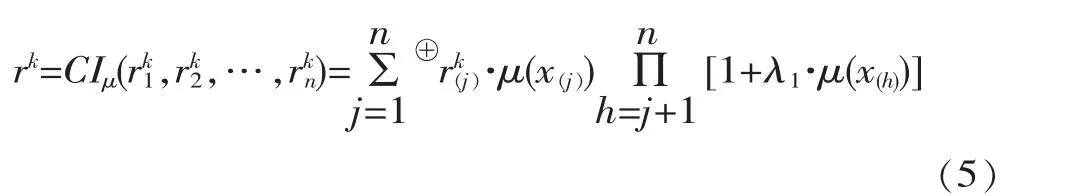
步骤5:再利用Choquet模糊积分对r位专家给出待评边坡的综合评价值(i=1，2，…，m)进行集结，得到边坡的群体综合评价值r为

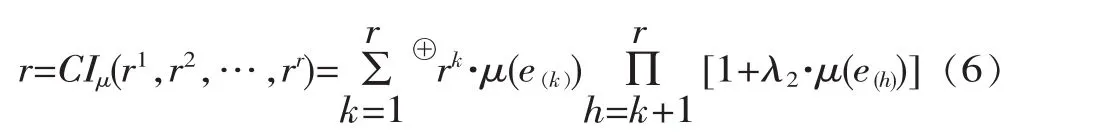
式中 ，r(1)≤r(2)≤…≤r(r)。

步骤6:依据综合评价值r对照评价标度集S={s1，s2，…，sl，}，对边坡的稳定性进行评判。

2 工程实例

某高边坡高185 m、长350 m，为台阶式人工边坡，分上下两段，上段是垂直台阶式灰岩边坡，下段是倾斜台阶式页岩边坡，坡面形态为直形坡，坡度为30°。边坡灰岩岩体内摩擦角为30°，转化为摩擦因数是0.58。边坡总体上为逆向坡，不存在平行边坡走向且倾向于坡面的大断层，结构面发育程度为32%，岩石风化程度为12%，边坡走向由N30°E转为N70°E，倾向 NW。边坡所处地区属亚热带气候，最大降雨强度114.4 mm/h，年平均降雨量1200 mm，渗透系数为2 m/d，饱水率为0.28%，植被覆盖率达30%，地震设防烈度为6度。

表1 评价指标标准值和实际值

针对该高边坡的实际情况，选取以下4类12项指标进行分析:地形地貌特征指标 （边坡高度、坡面形态、边坡坡度）、工程地质特征指标 （岩土类型、结构面发育程度、内摩擦因数）、水文气象特征指标 （多年平均降雨量、渗透系数、饱水率）和其他因素特征指标 （岩土风化程度、植被覆盖率、地震烈度）。边坡的稳定程度划分为5个级别:不稳定s1、次不稳定s2、基本稳定s3、较稳定s4和稳定s5，形成评价标度集 S={s1，s2，s3，s4，s5}。 根据该高边坡所处区域的具体条件，参照行业标准及其他类似工程[1,3,5]，将各评价指标的实际参数和标准值列于表1，其中定性指标按1～10的标度根据实际情况进行量化。

现有3位专家 （e1，e2，e3）以给定的评价标度S={s1，s2，s3，s4，s5}为标准，依据该边坡的各指标的实际值和各标度对应的标准值对各项指标进行评价，给出评价向量分别为

利用层次分析法得到的各评价指标xj的模糊密度 μ(xj)和各专家ek的模糊密度 μ(ek)分别为 μ(x1)=0.0835、μ(x2)=0.0755、μ(x3)=0.0835、μ(x4)=0.1088、μ(x5)=0.0890、μ(x6)=0.0984、μ(x7)=0.0863、μ(x8)=0.0780、μ(x9)=0.0780、μ(x10)=0.0730、μ(x11)=0.0730、μ(x12)=0.0730；μ(e1)=0.3323、μ(e2)=0.3672、μ(e3)=0.3005。根据公式 （2）确定其相应的参数λ1=0.09、λ2=0.11。

对专家e1给出的评价向量R1进行重排序使其满足 r1(1)≤r2(2)≤…≤r1(12)，有

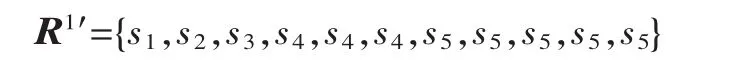
利用Choquet模糊积分对其评价信息进行集结，得到专家 e1的综合评价值为 r1=CIμ（）＝s3.94，同理可求出 r2=s4.14、r3=s3.51。

采用同样的方法，对3位专家给的综合评价值（s3.94，s4.14，s3.51）进行集结，得到边坡的群体综合评价值r为

由于综合评价值r=s4.02处于评价标度集S={s1，s2，s3，s4，s5}中的s4和s5之间，并与s4非常接近，认为该边坡较稳定。经验证，该评价结果与数值计算结果基本一致。

3 结 论

本文将Choquet模糊积分引入到边坡稳定性评价中，建立了基于Choquet模糊积分的边坡稳定性评价模型，用该评价模型对边坡稳定性进行评价可以得到更合理的评价结果，实践中具有较好操作性。工程实际应用表明，该方法的评价结论与数值计算结果基本一致，具有一定的工程应用价值，为边坡工程及其他复杂系统的评价提供了新的参考。

［1］黄建文，李建林，周宜红.基于AHP的模糊评判法在边坡稳定性评价中的应用[J].岩石力学与工程学报，2007，26（S1）:2627-2632.

［2］杨枭，李朋，肖盛燮.可靠性分析在边坡灰色聚类问题中的应用[J].重庆交通大学学报:自然科学版，2011，30（4）:778-781,838.

［3］秦植海,秦鹏.高边坡稳定性评价的模糊层次与集对分析耦合模型[J].岩土工程学报，2010，32（5）:706-711.

［4］杜金龙，孙金山，樊金平.基于神经网络参数优化的岩体边坡稳定性评价[J].人民长江，2012，43（13）:77-79，103.

［5］苏永华，罗正东，杨红波，等.基于响应面法的边坡稳定逆可靠度设计分析方法[J].水利学报，2013，44（7）:764-771.

［6］王广月，崔海丽，李倩.基于粗糙集理论的边坡稳定性评价中因素权重确定方法的研究[J].岩土力学，2009，30（8）:2418-2422.

［7］徐存东，张硕，左罗，等.基于可拓学理论的坝坡稳定性评价方法[J].水电能源科学，2013，31（2）:146-149.

［8］赵博，徐卫亚，梁桂兰.基于熵权的边坡稳定性评价物元可拓模型及其应用[J].水电能源科学，2013，31（1）:119-122,114.

［9］陈晓红，等.复杂大群体决策方法及应用[M].北京:科学出版社，2009.

［10］曲娜，曾伟.基于Choquet模糊积分的工程项目组织有序度评价[J].中南林业科技大学学报，2011，31（6）: 168-172.

［11］赵志青，马生全.模糊复Choquet积分的测度的确定问题 [J].江南大学学报:自然科学版，2013，12（4）:493-496.

［12］陈晓红，胡文华.基于直觉梯形模糊数和Choquet积分的创投项目研究[J].科研管理，2013，34（7）:127-135.

［13］李艳华，林剑，龙万学，等.基于位移的滑坡临滑时刻多模型综合预测模糊积分方法[J].自然灾害学报，2013，22（4）:208-212.