Kendall与R/S分析法在降雨特性分析中的应用
金保明
(福州大学土木工程学院,福建 福州 350116)
水文序列的变化特性分析可为流域水资源规划和管理工作服务。其研究方法较多。如,线性回归法、滑动平均法、Kendall秩次相关检验法 (以下简称 “Kendall”)、Spearman检验法[1]、重标极差 R/S分析法 (以下简称 “R/S” )[2]、Kendall和R/S相结合的分析法[3]、线性回归和R/S相结合的分析法[4]等等。本研究用Kendall、R/S以及两者相结合的分析方法分析南平市年平均降雨量变化的特性。
1 Kendall秩次相关检验法
Kendall最初由Mann于1945年提出[5],根据秩次相关检验统计量U来分析水文序列的变化趋势特性是否显著。如果U值为正,说明序列具有增加趋势;U值为负,则相反。其显著性检验采用正态分布进行。假定某一水文序列变化趋势不显著,对于给定显著水平α,查得对应于正态分布的临界值Uα/2。当|U| Hurst,H.E.于1965年提出时间序列的分形R/S分析法[2]。其主要原理如下: 假设一时间序列为{x(t)}nt=1,τ个数据累积离差 则重标极差为[2] 式中,S(τ)为τ个数据x(t)的标准差;H为Hurst指数;c为常数[2]。 根据式 (3)计算出水文序列的重标极差,点绘ln(R(τ)/S(τ))~lnτ 关系图并采用直线拟合,直线斜率即为Hurst指数H,该指数可以定性地分析序列的变化特性[2]:0 用R/S分析计算时,如果点绘的ln(R(τ)/S(τ))-lnτ的关系图无法拟合成一直线或拟合效果不理想时,说明该水文序列存在变异点[6]。遇到这种情况,可以通过计算找出变异点,将序列分成若干段小序列,然后把每段小序列单独抽出来重新进行R/S计算,根据H值分析每段小序列的变化趋势特征[7]。 Kendall从定量的角度分析水文序列的变化趋势特性是否显著。R/S则从定性的角度分析水文序列的持久性与反持久性特征,着重分析未来的变化趋势。如果将两者结合,称为Kendall和R/S相结合的分析法[3]。首先采用Kendall法计算出统计量U,分析水文序列的变化趋势;接着运用R/S法计算H值,分析水文序列变化特征;然后依据U与H值分析出水文序列未来的变化趋势,见表1。 表1 水文序列未来变化趋势特征分析 本次收集了南平市1961年~2007年年平均降雨量资料进行实例分析。南平市地处福建省北部,位于武夷山脉东南侧,闽浙赣三省交界处,属典型的亚热带季风湿润气候区,是个暴雨洪水灾害频繁发生的地区。通过频率计算,南平市年平均降雨量均值为1744.0 mm、Cv=0.16、Cs=2.0Cv,说明降雨量系列年际变化不大。 通过计算年平均降雨量序列的Kendall统计量U=0.229,小于显著水平α=0.05的正态分布临界值1.960,说明该序列趋势性不显著。 为了便于比较,在采用Kendall的基础上,同时采用线性回归法、滑动平均法对南平市1961年~2007年年平均降雨量序列进行分析。图1为南平市年平均降雨量序列过程线、滑动平均过程线 (n=5年)、线性趋势线 (y=-0.2455x+1749.9)与多年平均均值线。其中的多年平均均值线与线性趋势线基本重合,初步说明南平市近50年来降雨量总体情况是在均值附近左右摆动、呈微弱减少趋势,但趋势不明显。20世纪80年代至90年代初降水明显偏少,90年代以后降水的年际波动大。 图1 南平市1961年~2007年年平均降雨量过程线 采用R/S法分析发现,序列在1971年、1978年、1991年、1998年、2003年存在变异点;因此将序列分成6段适线 (见图2)。 首先求出南平市年平均降雨量第一段序列 (1961年~1970年)拟合的直线方程 (y=0.9188x-0.6651),其中直线斜率0.9188,也就是该序列的H值。 图2 南平市年平均降雨量分段序列ln(R(t)/S(t))~ln(t)关系 表2 南平市1961年~2007年年平均降雨量分段序列变化特性分析 其余五段小序列,首先把每段小序列抽出单独进行R/S计算,然后分别点绘ln(R(t)/S(t))~ln(t)关系图。各段序列拟合得出新的直线方程分别为:第2段序列(1971年~1977年)y=0.4362x-0.1475,第 3段序列(1978年~1990年)y=0.7953x-0.5553,第4段序列(1991年~1997年)y=0.5096x-0.3176,第5段序列(1998年~2002年)y=0.7280x-0.4837,第6段序列(2003年~2007年)y=0.9134x-0.6872。这样,第 2~6段序列的 H值分别为 0.4362、0.7953、0.5096、0.7280、0.9134,各段序列的持久性或非持久性见表2。 由表2可知,1961年~1970年南平市年平均降雨量序列Kendall检验统计量 (以下简称 “统计量”)U值为0.447,大于零,说明序列有增加趋势,而U值小于1.96,说明增加趋势不显著;序列的H值为0.9188,大于0.5,说明序列具有持久性,可以分析下一阶段1971年~1977年年平均降雨量序列具有增加趋势 (当然这种趋势不显著,只是作为一种定性分析用),与实际情况相符合。 1971年~1977年年平均降雨量序列统计量U值为1.051,说明序列有增加趋势,但U值小于1.96,说明增加趋势不显著;序列H值为0.4362,小于0.5,说明序列具有反持久性;预测对下一阶段1978年~1990年年平均降雨量序列具有减少趋势的分析,与实际情况相符合。 1978年~1990年年平均降雨量序列统计量U值为-0.610,其绝对值小于1.96,说明减少趋势不显著;序列H值为0.7953,大于0.5,说明序列具有持久性,分析下一阶段1991年~1997年年平均降雨量序列可能会有减少趋势,这与实际情况不相符合,可能与年平均降雨量变化趋势不显著有关。 1991年~1997年年平均降雨量序列统计量U值为1.051,说明序列有增加趋势,但U值小于1.96,说明增加趋势不显著;序列H值为0.5096,约等于0.5,说明年平均降雨量序列是随机的。即,现在不会影响将来,因此也就无法判断未来的趋势。 1998年~2002年年平均降雨量序列统计量U等于0,无法确定序列的趋势,但利用线性回归法分析回归系数估计值b=-74.95,小于零,说明该段序列有减少趋势,其统计量T值为-1.071,绝对值小于显著水平α=0.05的t分布临界值tα/2=3.182,说明趋势不显著;序列H值为0.7280,大于0.5,说明该段序列具有持久性,分析2003年~2007年年平均降雨量序列具有减少趋势,与实际情况不相符合,可能与年平均降雨量变化趋势不显著有关。 2003年~2007年年平均降雨量序列统计量U值为0.979,说明序列有增加趋势,但U值小于1.96,说明增加的趋势不显著;序列H值为0.9143,大于0.5,说明序列具有持久性,预测未来一段时间年均降雨量序列存在增加趋势,这与实际情况相符合。 本研究表明,近50年来南平市降水总体趋势在均值附近摆动、呈微弱减少,但趋势不明显;相对来说随机性明显,20世纪90年代以后降水的年际波动大,今后几年年平均降雨量序列存在增加趋势。相对来说,Kendall用于分析样本序列的趋势特征效果比较好,R/S序列用于分割样本比较适用,Kendall与R/S相结合的分析方法综合两种方法的优点,可以对样本序列的变化特性进行深入分析。对于趋势不显著、随机性和独立性强的样本序列,Kendall与R/S相结合的分析方法分析结果不理想。 [1]丁晶,邓育仁.随机水文学[M].成都:成都科技大学出版社,1988. [2]李水根.分形[M].北京:高等教育出版社,2004. [3]于延胜,陈兴伟.R/S和Mann-Kendall法综合分析水文时间序列未来的趋势特征[J].水资源与水工程学报,2008,19(3):41-44. [4]金保明,方国华.线性回归法和R/S分析法在南平市年平均气温变化趋势分析中的应用[C]∥中国水文科技新发展—2012中国水文学术讨论会论文集.南京:河海大学出版社,2012:284-287. [5]王生雄,魏红义,王志勇.渭河径流序列趋势及突变分析 [J].人民黄河,2008,30(9): 26-29. [6]王孝礼,胡宝清,夏军.水文时序趋势与变异点的R/S分析法[J].武汉大学学报:工学版,2002,35(2):10-12. [7]金保明.南方山区流域防汛管理研究[D].南京:河海大学,2009.2 重标极差R/S分析法
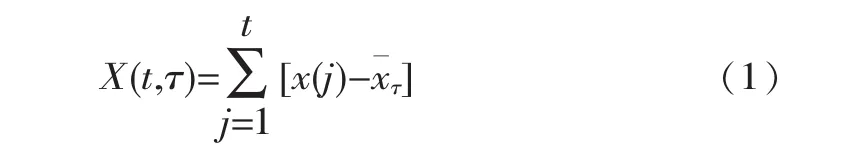
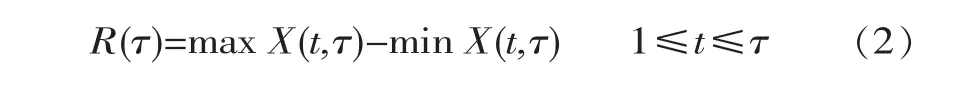

3 Kendall和R/S相结合的分析法

4 实例应用
4.1 用Kendall法分析年平均降雨量序列趋势特性
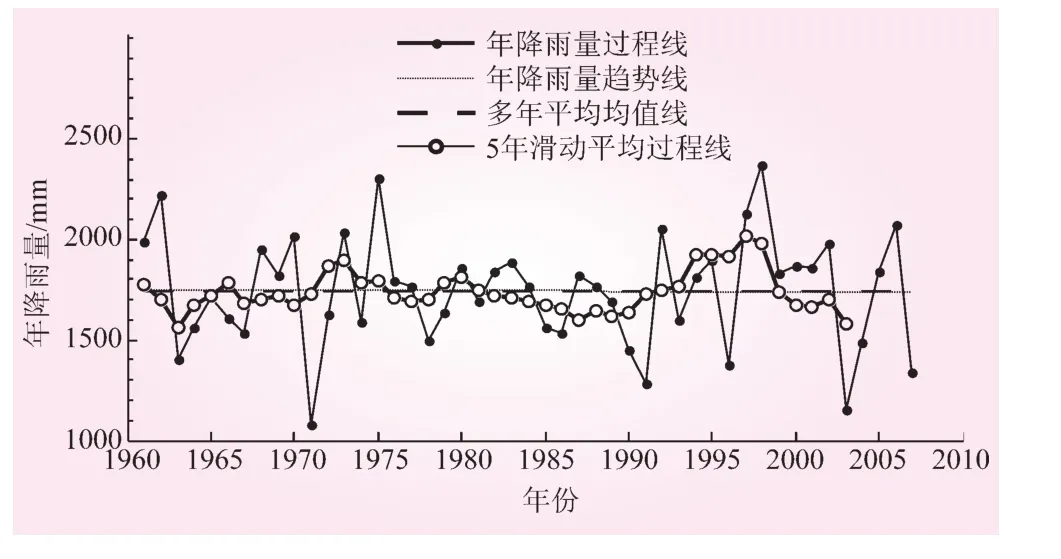
4.2 用R/S法分析年平均降雨量序列变异点


4.3 用Kendall与R/S相结合的分析法分析年平均降雨量变化特性
5 结 语

