跨接VTSRK方程计算烃类的pVT性质

申爱景 段远源 杨 震

(清华大学热科学与动力工程教育部重点实验室,二氧化碳资源化利用与减排技术北京市重点实验室,北京 100084）

1 引言

烃类是石油、天然气等的重要组成成分,其pVT性质的精细表征对燃烧、液滴蒸发、石油开采等过程应用有重要意义,1,2尤其是临界区性质的预测.3如燃料燃烧过程中,由于临界区的密度涨落引起的不同于常规区域的热力学性质变化,对火焰结构有很大的影响.4

状态方程是描述流体pVT性质的重要工具,立方型方程形式简单,由于计算精度较高而获得广泛应用,但不足在于饱和液相密度和近临界区pVT性质计算精度较差.5,6专用状态方程尽管具有很高的计算精度,但仅适用于特定工质,依赖于大量高精度的实验数据,形式复杂,回归参数较多.7改进立方型方程,提高其液相区和近临界区的计算精度,具有重要实用价值.

为了改进立方型方程的液相密度计算精度,Martin8提出了比容平移方法.学者们对此方法进行了改进,9-11由于比容平移量是随温度变化的量,当温度从临界温度(Tc）逐渐降低时,比容平移量呈指数降低的趋势,当温度低于0.7Tc时,逐渐成为定值,11所以学者们对比容平移量采用了不同的处理方法.第一种是将比容平移量表示为与温度相关的函数,这种方法明显提高了方程在近临界区和远临界区的计算精度,但可能会导致高压区热力学不一致问题,如高压下等温线交叉,12斥力项(b-c）<0,13,14比定容热容小于0.12第二种是将比容平移量设为与温度无关的常量,由于比容平移量是随温度变化的值,为了同时兼顾近临界区和远临界区的计算精度,将比容平移量取为远临界区和近临界区的平均值,8,9虽然计算精度较原始方程有所提高,但仍不够理想.另外,由于经过比容平移改进的状态方程仍属于平均场理论,所以无法精确描述临界点附近的热力学性质,且无法精确计算得到临界指数.

在临界点附近,标度定律可以描述流体奇异的热力学性质,但仅适用于极接近临界点的小区域.学者们提出了经典方程与标度方程结合的跨接状态方程,以改进经典方程在近临界区的不足.15-18Kiselev18提出的跨接方法已被用于与立方型方程、统计缔合流体理论(SAFT）方程结合,18-21但该方法会额外引入6个跨接参数,需要大量的实验数据回归.22

本文的主要目的是建立烃类(C1-C20）的跨接状态方程,将比容平移方法用于SRK方程,将比容平移项设为与温度低于0.7Tc时的比容平移量相等的值,主要改善方程在远临界区的描述精度,在此基础上引入跨接方法,改进方程对近临界区pVT性质的描述精度.将跨接比容平移SRK(跨接VTSRK）方程中的参数表示为临界参数和比容平移项相关的函数,尽可能减少方程中的可调参数,使得方程具有预测性,并且容易推广到混合物的物性计算中.

2 VTSRK方程

SRK方程5的形式如下:

式中,p为压力;T为温度;v为比体积;R为通用气体常数,8.314472 J·K-1·mol-1;a和b为方程参数;Tc为临界温度;pc为临界压力;α(T）的表达式为

式中,Tr为对比温度,Tr=T/Tc;ω为偏心因子.

将于温度无关的比容平移项引入SRK方程,得到比容平移SRK(VTSRK）方程

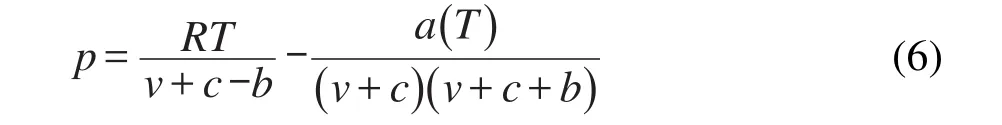
式中,c为比容平移项,表达式如下

式中,Zc为临界压缩因子,c1为修正函数,通过实验数据回归得到.

3 跨接VTSRK方程

将跨接方法18引入VTSRK方程中,跨接方程的Helmholtz自由能表示成无量纲形式

式中,ΔT=T/T0c-1和Δv=v/v0c-1分别表示距离经典方程所计算出的临界温度T0c和临界比容v0c的无量纲距离;(T）=p(T,v0c）/RT,表示临界比容v0c下的无量纲压力;(T）=(T,v0c）,表示 v0c下的无量纲剩余Helmholtz自由能;(T）表示仅与温度相关的无量纲理想气体Helmholtz自由能.

在Helmholtz自由能的临界部分中,经典的无量纲温度ΔT和无量纲比容Δv分别被相应的重整化值代替

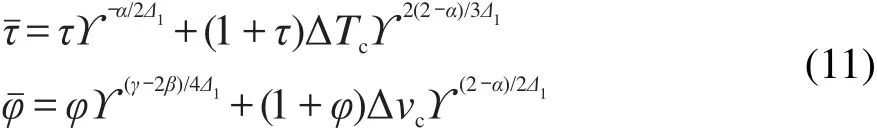
上式中,α=0.11,β=0.326,γ=1.239,Δ1=0.52为临界指数;23τ=T/Tc-1和φ=v/vc-1分别为与实际的临界温度和临界比容的无量纲距离;ΔTc=(Tc-T0c）/T0c和Δvc=(vc-v0c）/v0c分别为实际临界温度、临界比容与经典方程计算得到的临界温度和临界比容的无量纲偏差;ϒ是跨接函数.

Helmholtz自由能的最终表达式为

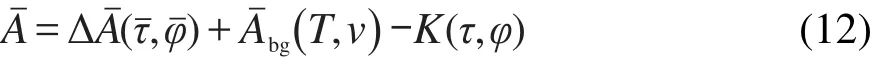
式中Kernel动力项

式中系数a20和a21分别对应渐近线项和一阶Wegner修正项.

跨接函数ϒ(τ,φ）是跨接方法中的核心参数.为了使跨接方程在远临界区域完全退化为经典方程,本文引入新的跨接函数表达式

式中,q=r/G,G是Ginzburg数,与流体种类相关,表征临界区域的大小,具体形式可参考文献.22

通过对式(12）进行微分可得到跨接VTSRK方程

4 计算结果与讨论

尽可能减少待定系数,可以使方程具有更好的普适性和预测性.VTSRK方程较原SRK方程多一个可调参数c1,跨接方法又引入了6个跨接参数,G、m0、v1、d1、a20和a21,共含有7个参数.其中,a20和a21作为Kernel动力项中的系数,主要是为了修正热容性质的描述,而本文不涉及热容性质,因此将两个参数a20、a21设为0.m0是与跨接正弦模型中普适的临界振幅比相关的量,常被取为1.24,25Kiselev和Ely24发现当用m0(4/3）1-β代替m0时,解析正弦模型与跨接正弦模型的解一致.因此,本文令m0=1×(4/3）1-β=1.214.与G相比,v1、d1对流体热力学性质的影响较小,一些学者将v1取为定值0.001,25将d1取为0,26已达到减少方程参数的目的,效果较好.因此,本文将两个参数均取为定值,即v1=0.001,d1=0.综上,跨接VTSRK方程中仅剩下两个可调参数:c1和G.

首先,采用流体远临界区的饱和蒸气压和饱和液相密度数据回归得到c1,然后再利用近临界区的饱和蒸气压和饱和液相密度数据得到G.

跨接VTSRK方程中的临界参数和偏心因子参考文献.27,28

根据回归结果,发现G与c1及临界压缩因子Zc之间存在函数关系,拟合得到

而c1与Zc之间的变化关系如图1所示.因此,可进一步将c1表示成Zc的函数

方程中的所有参数均表示为临界参数和偏心因子的函数,无可调参数,使得方程具有预测性.为了验证方程的预测能力和精度,采用跨接VTSRK方程计算了C1-C20烷烃的相平衡和单相区的pVT性质,并与原始SRK方程和VTSRK方程进行了比较.

图227和图327给出了VTSRK方程和跨接VTSRK方程对于C1-C10烷烃的相平衡预测结果.

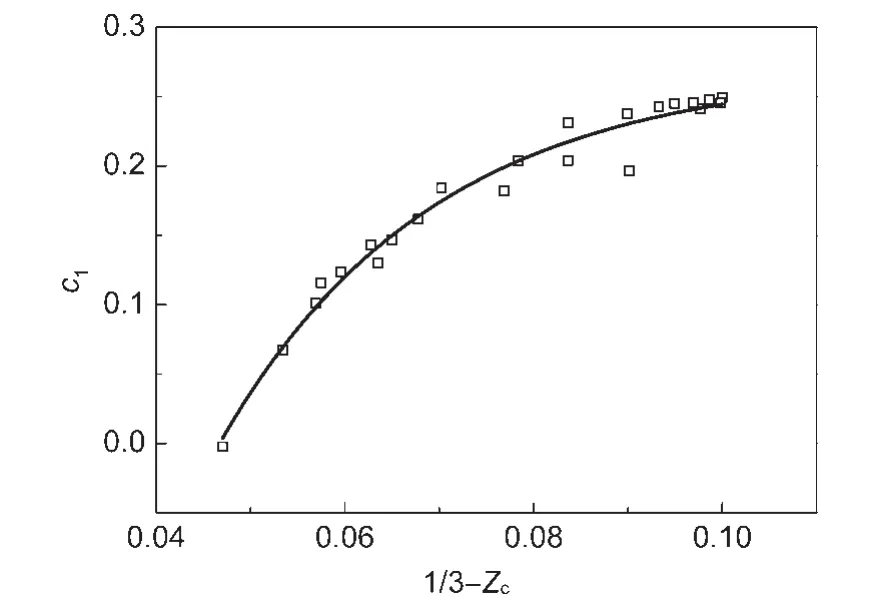
图1 c1与Z c之间的关系Fig.1 Relationship between c1and Z c

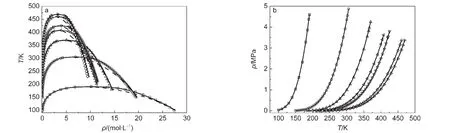
图2 VTSRK方程和跨接VTSRK方程对C1-C5烷烃的相平衡(VLE）预测结果27Fig.2 Vapor-liquid equilibrium(VLE）prediction results of VTSRK EoS(-）and crossover VTSRK EoS(）for C1-C5 alkanes27

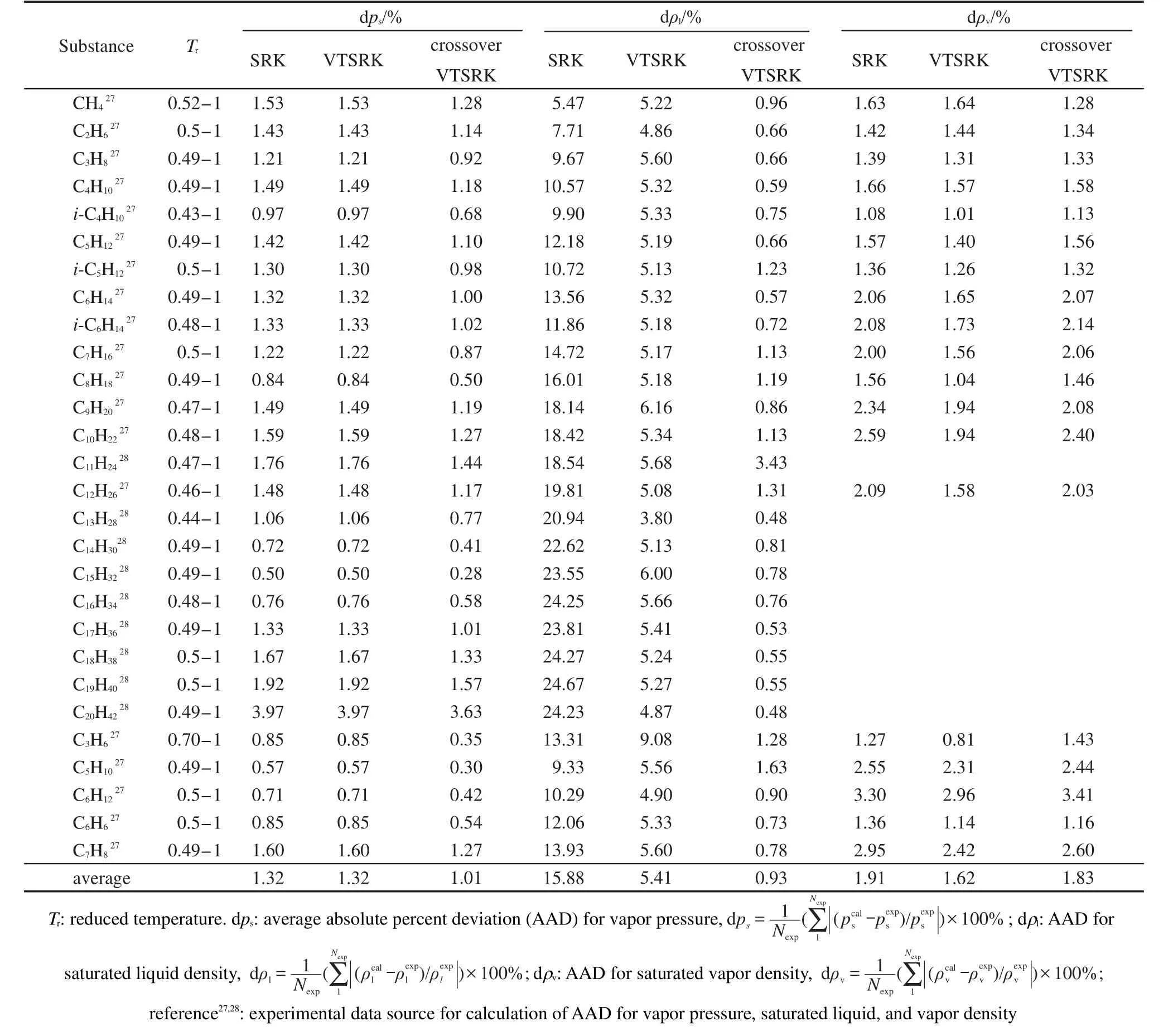
表1 各物质的相平衡预测偏差Table 1 VLE prediction deviations of fluid

图3 VTSRK方程(-）和跨接VTSRK方程(-）对C6-C10烷烃的VLE预测结果27Fig.3 VLE prediction results of VTSRK EoS(-）and crossover VTSRK EoS(）for C6-C10 alkanes27

表1给出了跨接VTSRK方程、VTSRK方程和原SRK方程对C1-C20相平衡预测偏差的比较.27,28

根据表1的结果,对于相平衡性质,跨接VTSRK方程与原SRK方程和VTSRK方程的饱和蒸气压和饱和气相密度的计算偏差相近,其中,饱和蒸气压的平均计算偏差为1.01%,饱和气相密度平均计算偏差为1.83%,跨接VTSRK方程对于饱和液相密度的平均计算偏差为0.93%,明显小于其他两个方程的计算偏差.跨接VTSRK方程如果直接采用c1和G的回归值,对C1-C20烷烃的pVT性质进行计算,其饱和蒸气压、饱和气相密度和饱和液相密度的平均计算偏差分别为1.01%、1.83%和0.67%,采用式(16）和(17）的预测性跨接方程与之相比,对饱和蒸气压和饱和气相密度的计算精度基本相同,饱和液相密度的计算精度略有下降,但与SRK方程和VTSRK方程相比,精度仍有明显提高.

为了检验跨接VTSRK方程的预测性,采用该方程计算了环烷烃（环丙烷、环戊烷和环己烷）以及苯、甲苯物质的相平衡性质,并与VTSRK方程和原SRK方程进行了比较,如表1所示.与C1-C20烷烃结果类似,跨接VTSRK方程对饱和蒸气压的平均计算偏差为0.58%,饱和气相密度的平均计算偏差为2.21%,与VTSRK方程和原SRK方程的计算偏差相近.跨接方程对饱和液相密度的平均计算偏差为1.06%,明显改善了原SRK方程和VTSRK方程对饱和液相密度的描述,尤其是临界区.

图4 甲烷的单相区预测结果Fig.4 Prediction results for methane in single phase region

图5 十二烷的单相区预测结果Fig.5 Prediction results for dodecane in single phase region

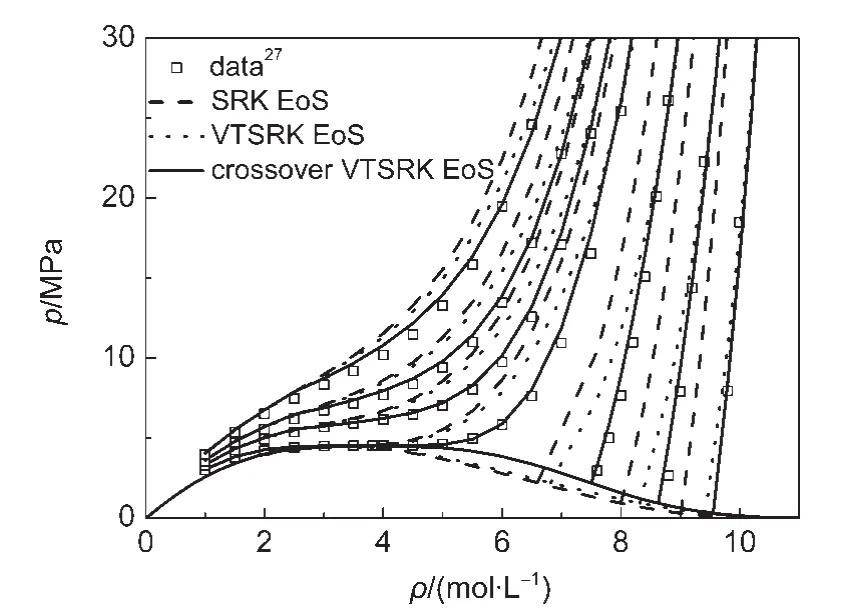
图6 环戊烷的单相区预测结果Fig.6 Prediction results for cyclopentane in single phase region

图7 苯的单相区预测结果Fig.7 Prediction results for benzene in single phase region

对于单相区的性质,以甲烷、十二烷、环戊烷和苯为例,图4-图7给出了跨接VTSRK方程、VTSRK方程和原SRK方程在单相区的预测结果.

根据图4-7的结果,VTSRK方程相对于SRK方程,改善了远临界区的pVT性质描述精度,跨接VTSRK方程在VTSRK方程的基础上,进一步提高了近临界区的计算精度.

5 结论

本文建立了烷烃(C1-C20）的跨接VTSRK方程,方程中的参数均表示为临界参数和偏心因子的函数,使方程具有预测性.与原SRK方程和VTSRK方程相比,本文的跨接方程明显改善了液相密度的描述.对于相平衡性质,饱和蒸气压、饱和气相密度和饱和液相密度的平均计算偏差分别为1.01%、1.83%和0.93%.对于单相区,本文的跨接方程对于密度的计算有明显改进,尤其是接近临界点的区域.采用本文跨接方程预测环烷烃和苯类物质pVT性质的结果表明,本文方程对于环烷烃和苯类流体的预测精度与烷烃(C1-C20）的计算精度相当,验证了方程的预测性.

(1）Meng,X.Z.;Jia,M.;Wang,T.Y.Fuel 2013,111,216.doi:10.1016/j.fuel.2013.04.050

(2）Sisti,J.;DesJardin,P.E.Combust.Theor.Model.2013,17(4）,657.doi:10.1080/13647830.2013.791725

(3）Li,L.Y.;Sun,F.F.;Chen,Z.T.;Cai,J.Acta Phys.-Chim.Sin.2013,29(11）,2332.[李丽妍,孙方方,陈志同,蔡 钧.物理化学学报,2013,29(11）,2332.]doi:10.3866/PKU.WHXB201307311

(4）Singla,G.;Scouflaire,P.;Rolon,C.;Candel,S.P.Combust.Inst.2005,30,2921.doi:10.1016/j.proci.2004.08.063

(6）Peng,D.;Robinson,D.B.Ind.Eng.Chem.Fundamen.1976,15(1）,59.doi:10.1021/i160057a011

(7）Buecker,D.;Wagner,W.J.Phys.Chem.Ref.Data 2006,35(2）,929.doi:10.1063/1.1901687

(8）Martin,J.J.Ind.Eng.Chem.1967,59(12）,34.doi:10.1021/ie50696a008

(9）Peneloux,A.;Rauzy,E.;Freze,R.Fluid Phase Equilib.1982,8(1）,7.doi:10.1016/0378-3812(82）80002-2

(10）Lin,H.;Duan,Y.Y.Fluid Phase Equilib.2005,233(2）,194.doi:10.1016/j.fluid.2005.05.008

(11）Lin,H.;Duan,Y.Y.;Zhang,T.;Huang,Z.M.Ind.Eng.Chem.Res.2006,45(5）,1829.doi:10.1021/ie051058v

(12）Ji,W.R.;Lempe,D.A.Fluid Phase Equilib.1997,130(1-2）,49.doi:10.1016/S0378-3812(96）03190-1

(13）Pfohl,O.Fluid Phase Equilib.1999,163(1）,157.doi:10.1016/S0378-3812(99）00199-5

(14）Yelash,L.V.;Kraska,T.AIChE J.2003,49(6）,1569.doi:10.1002/aic.690490620

(15）Chapela,G.A.;Rowlinso,J.S.J.Chem.Soc.Faraday Trans I 1974,70,584.

(16）Fox,J.R.Fluid Phase Equilib.1983,14,45.

(17）Salvino,L.W.;White,J.A.J.Chem.Phys.1992,96(6）,4559.doi:10.1063/1.462791

(18）Kiselev,S.B.Fluid Phase Equilib.1998,147(1-2）,7.doi:10.1016/S0378-3812(98）00222-2

(19）Kiselev,S.B.;Ely,J.F.Fluid Phase Equilib.2004,222,149.

(20）Kiselev,S.B.;Ely,J.F.Fluid.Phase Equilib.2007,252(1-2）,57.doi:10.1016/j.fluid.2006.10.028

(21）Kiselev,S.B.;Ely,J.F.Ind.Eng.Chem.Res.1999,38(12）,4993.doi:10.1021/ie990387i

(22）Xu,X.H.;Duan,Y.Y.;Yang,Z.Ind.Eng.Chem.Res.2012,51(18）,6580.doi:10.1021/ie300112j

(23）Sengers,J.V.;Shanks,J.G.J.Stat.Phys.2009,137(5-6）,857.doi:10.1007/s10955-009-9840-z

(24）Kiselev,S.B.;Ely,J.F.Chem.Eng.Sci.2006,61(15）,5107.doi:10.1016/j.ces.2006.03.044

(25）Hu,Z.Q.;Yang,J.C.;Li,Y.G.Fluid Phase Equilib.2003,205(1）,25.doi:10.1016/S0378-3812(02）00307-2

(26）Kiselev,S.B.;Ely,J.F.J.Phys.Chem.C 2007,111(43）,15969.doi:10.1021/jp073706p

(27）Lemmon,E.W.;Huber,M.L.;McLinden,M.O.NIST Standard Reference Database 23:Reference Fluid Thermodynamic and Transport Properties-REFPROP,version 9.0;Gaithersburg:National Institute of Standards and Technology,2010.

(28）DIPPR Thermophysical Properties Laboratory 350CB,DIPPR Project 801 Evaluated Process Design Data;Brigham Young University:Provo,UT 84602,2010.