基于GTS的黏土中缩颈桩检测研究

于德国，张 彬，徐鑫哲，刘 冰

(盘锦职业技术学院建筑与海洋工程系，辽宁 盘锦 124010)

缩颈是钻孔桩施工中经常遇到的问题，桩身截面面积的减小，会导致桩的承载能力降低等一系列的问题［1］，如果不能及时发现，将会给工程埋下巨大的隐患。本文应用GTS有限元分析软件对缩颈桩进行模拟分析。

1 建模

GTS(Geotechnical and Tunnel Analysis System)是一个十分成熟的软件［2－8］，具有许多强大的功能，可以进行设计及施工阶段的应力分析和渗透分析，也可以对岩土工程和隧道进行分析，同时也可以对桩基础的检测进行数值模拟。

1.1 桩土体系

对缺陷桩的模拟，土体采用德鲁克—普拉格模型，并且假定桩土界面无相对滑动，不考虑重力影响，当对桩顶施加激振力时，整个计算域内处于弹性状态［9］。对桩体进行模拟分析过程中，如果出现畸形单元，GTS软件可以对这些部位再次划分网格，以保证模拟结果的精确性。本文建立2维模型进行模拟。

1.2 入射波激振源

根据以往对工程桩测试的经验［10］，采用不同的激振源，得到的波形不一致，对检测结果有很大影响。采用橡胶锤击振采集到的波形要比选用其它设备的效果好。本次数值模拟中采用橡胶锤击振，脉冲宽度为 1.5 ms。

1.3 参数选取

本次模拟采用的桩参数为:桩长L=9 m，桩直径D=1 m，桩身弹性模量E=2.5×104MPa，桩体密度ρ=2 450 kg/m3。土体参数为:桩身裂缝模拟接近软土单元，黏土弹性模量 Es=5 MPa，密度为ρs=1 800 kg/m3，内摩擦角 φk=16°，粘聚力 c=36 kPa。

2 数值模拟

波阻抗Z的定义为

式中 S为桩身的截面面积;v为弹性波速。

由式(1)可以看出，Z随S的变化而变化。

如果在桩的顶部施加向下的激振力，那么产生的波将会沿着桩身向下传播，当桩身截面面积缩小时，一部分波将继续透射，另一部分则产生反射［11－13］。

波阻抗比α的计算公式为

式中 S1、ρ1、v1分别为弹性桩的初始截面面积、桩身密度、弹性波速;S2、ρ2、v2分别为弹性桩变化后的截面面积、桩身密度、弹性波速。

α反映了波在弹性体内传播时的突变性质，而且能够影响入射波与反射波的相对幅值。

假设在桩身波阻抗变化处，对应截面上的入射波振幅为At，反射波振幅为Ar。则有

对于仅有截面变化的桩，α反应的是桩体横截面面积的变化，可以简化为桩径的变化。α控制了入射波与反射波的相对幅值，实际上是控制了在波阻抗变化处的能量分配。因此，对于只有桩的截面发生变化而桩侧土未发生变化的情况，桩身直径的变化程度与变化处的入射波与反射波的相对幅值存在相互对应关系［14－15］。

假设桩周土体为黏性土，桩径的变化程度δ的计算式为

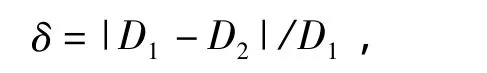
式中 D1、D2分别为桩的原始直径和缩颈处的直径。

假设入射波的初始幅值为A1，桩顶部接收的反射波的初始幅值为A2，如图1所示，缩颈桩的计算模型如图2所示。

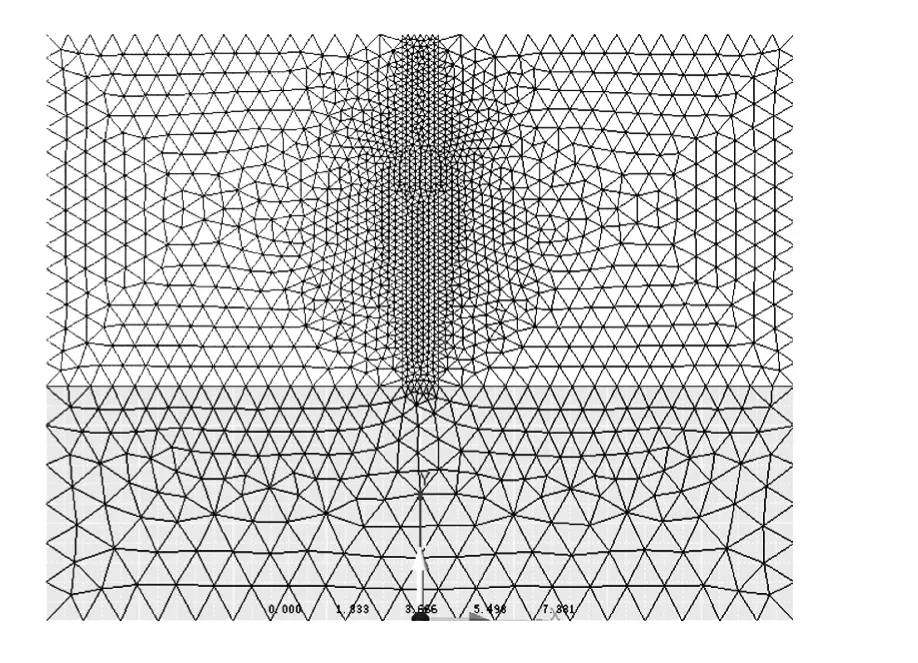
图2 缩颈桩计算模型

对于桩周围土体同质、均匀的桩，在受到激振力时，可以模拟成存在阻尼的1个自由度体系的自由振动。假设β为阻尼系数，自由体系的振幅符合A(t)=A1e－βt的衰减，则在t=t0处，激振力入射波与反射波的振幅比为

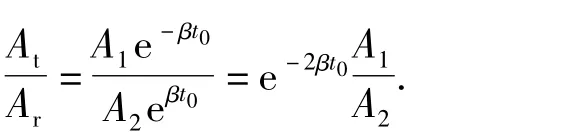
由于桩身全部在土中，因此β应当包含2部分，即桩本身的阻尼作用和桩周土的阻尼作用。其中桩本身的阻尼作用的影响非常小，几乎不用考虑，所以，β仅仅指的是桩周土的阻尼系数，即桩侧土阻尼系数Js。随着波沿桩迅速向下传递，必然引起一部分能量的损失，即波的衰减。因此，主要分析Js和缺陷位置(缺陷距桩顶距离h)变化时，δ与A1/A2之间的关系式。

3 量化分析

通过GTS软件对于缩颈缺陷桩在黏土中不同Js、不同h的模拟，得到δ－A1/A2关系曲线如图3～5所示。

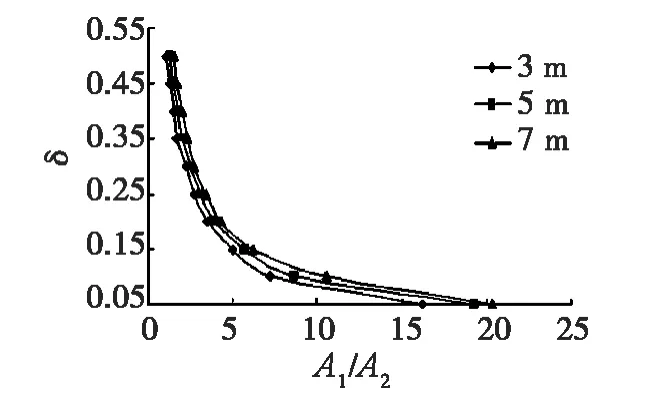
图3 Js=0.44时δ－A1/A2关系曲线

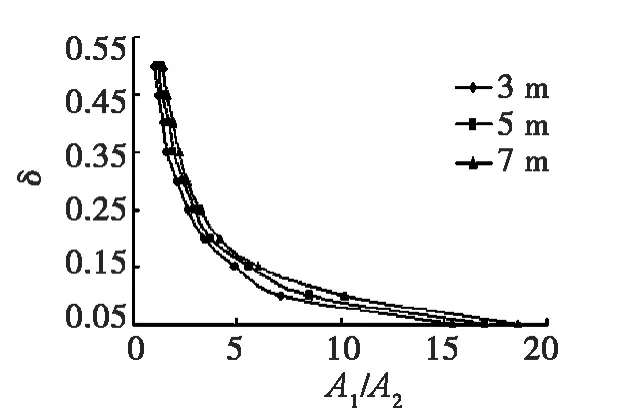
图4 Js=0.7时δ－A1/A2关系曲线

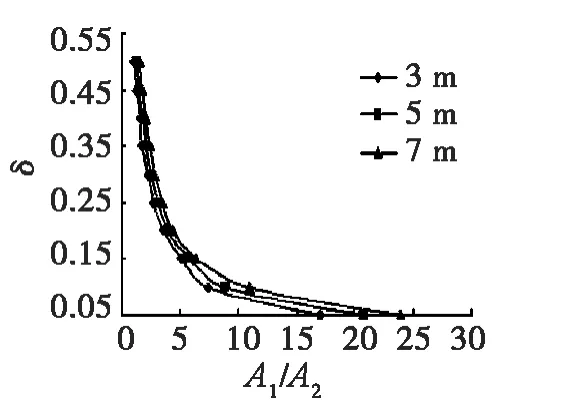
图5 Js=1.0时δ－A1/A2关系曲线

图6 Js=0.44时3 m处拟合曲线

从图6可以看出，拟合曲线与模拟曲线比较一致。

因此，用最小二乘法拟合得到的δ－A1/A2关系式为

式中 a1、b1为与h、Js变化有关的系数，取值如表1所示。

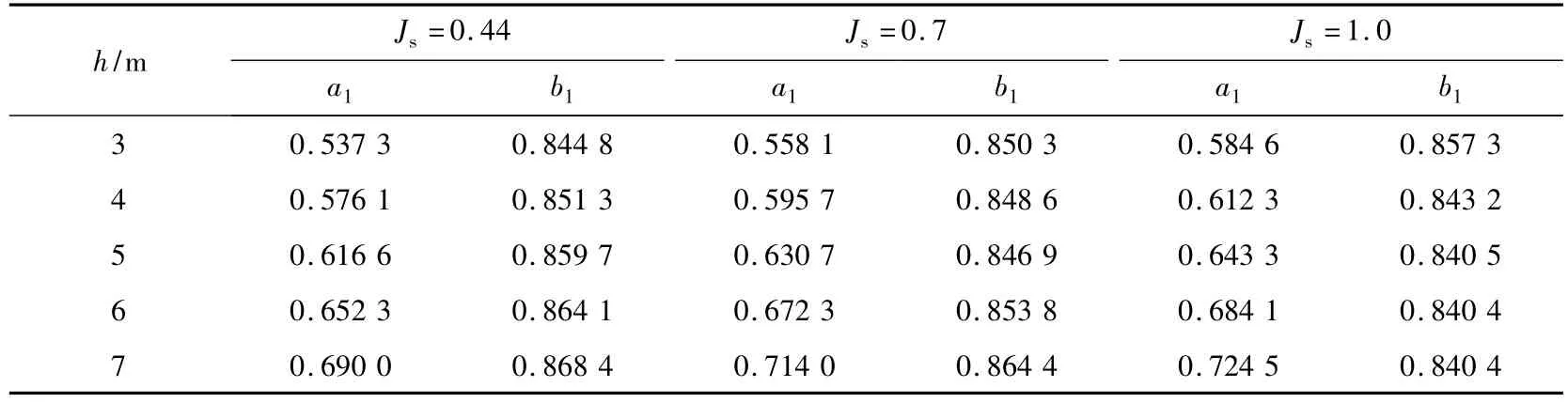
表1 在黏土中的缩颈缺陷桩的a1、b1取值

从表1可知，随h的变化，a1产生有规律的变化，在不同的Js下，得到a1－h关系曲线如图7所示。

从图7可知，当Js不变时，a1和h存在着一一对应的关系，呈现非线性增长的规律。当h不变时，a1与Js也符合这一规律。

用最小二乘法对图7中Js=0.44的曲线进行拟合，表达式为a1=0.025h2+0.349 3h+0.431 3，如图8所示。

图7 Js不同时a1－h关系曲线

图8 Js=0.44时的a1－h拟合曲线

对图7中的不同Js下的a1－h进行拟合，得到a1－h的二次多项式为

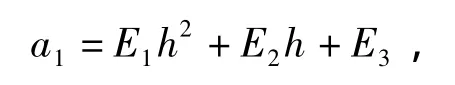
式中 E1、E2、E3为待定系数，如表2所示。

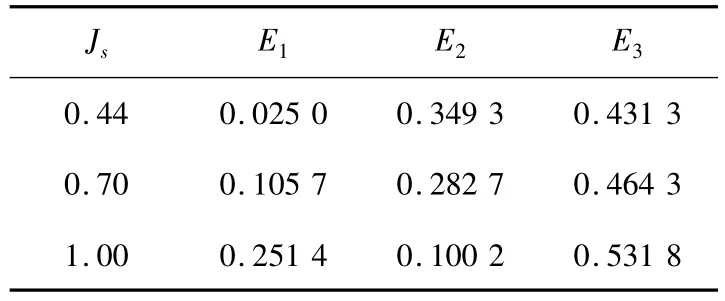
表2 不同Js下 E1、E2、E3的取值

4 结语

通过以上数值模拟，可以得出在黏性土中不同Js时的δ－A1/A2关系曲线变化规律为:1)δ－A1/A2的振幅的变化符合δ=a1(A1/A2)b1的幂函数变化规律，仅仅对于缺陷位置的不同，分别取不同的系数a1、b1。2)当桩周围土均匀、同质时，如果h不变，A1/A2随δ的增大而减小，如果δ不变，A1/A2随着h的加深而增大。3)a1与h，可以应用二次多项式进行拟合，对于不同的Js，选用不同的系数。4)如果缩颈缺陷程度δ＞0.5时，由于桩的截面积缩小过快，可以视为断桩，没有进行分析。

本文的数值模拟仅仅假设了桩周土同质、均匀，而没有考虑土的分层以及土质不均情况。若桩周土分层，需要按照土的分层分别选用不同的Js以及h进行计算。

［1］程跃广，潘学臣，布占鹏.桥梁钻孔灌注桩工程事故的预防及处理措施［J］.山东交通学院学报，2004，12(3):47－49.

［2］钱德玲，张文彦，曹光暄，等.基于GTS对单桩静载试验的有限元模拟分析［J］.合肥工业大学学报:自然科学版，2009，32(2):234－237.

［3］王珂，李顺群，李珊珊.Midas/GTS在边坡稳定性与地基沉降分析中的应用［J］.辽宁工程技术大学学报:自然科学版，2012，31(3):362－365.

［4］帅红岩，韩文喜，赵晋乾.Midas/GTS软件在边坡三维稳定分析中的应用［J］.地质灾害与环境保护，2009，20(3):104－107.

［5］李辉，杨罗沙，李征.基于Midas/GTS对地铁站超深基坑空间效应的研究［J］.铁道建筑，2011(4):83－85.

［6］卢洋，傅德胜，郑关胜.基于MIDAS多层结构的构建与开发明［J］.武汉理工大学学报，2004，28(1):141－144.

［7］蒋青青，杨艳萍，曹平，等.三心圆隧道拱顶沉降的群桩效应及其防护措施［J］.铁道科学与工程学报，2012，9(6):36－41.

［8］唐德康.基于MIDAS/GTS三维边坡中抗滑桩桩位的优化分析［J］.广东建材，2013(8):42－45.

［9］刘汉龙，丁选明.现浇薄壁管桩在低应变瞬态集中荷载作用下的动力响应解析解［J］.岩土工程学报，2007，29(11):1611－1617.

［10］卢发亮，周建国.超声法评判桩身混凝土缺陷探析［J］.山东交通学院学报，2003，11(1):58－60.

［11］邬晓光，刘近龙.基于Mathcad的桩基超声波检测声测管不平行问题研究［J］.山东交通学院学报，2011，19(3):53－56.

［12］李巨文，王翀，林玮，等.模型桩低应变反射波法曲线研究［J］.地震工程与工程震动，2006，26(3):252－256.

［13］费康，刘汉龙，张霆.PCC 桩低应变检测中的三维效应［J］.岩土力学，2007，28(6):1095 －1102.

［14］张献民，蔡靖，王建华.基桩缺陷量化低应变动测研究［J］.岩土工程学报，2003，25(1):47－50.

［15］与德国，赵显涛，周永伟.砂土中桩基缺陷的量化分析研究［J］.山西建筑，2010，36(7):101－102.