闭环控制在压路机振动液压系统中的应用

李 雨，顾秋军，徐鹏杰，刘占献

(长安大学道路施工技术与装备教育部重点实验室，陕西 西安 710064)

压路机是公路施工中常见的一种非牵引式工程机械，作业质量是优先保证的性能参数［1］。对于振动压路机而言，不同区段压实度的均匀性是评价作业质量的指标之一［2］，这要求压路机在平稳工作时振动频率保持稳定［3］。一般认为，压路机在正常的压实作业过程中振动频率保持不变，但对某20 t单钢轮压路机试验发现，振动频率处于波动之中。

在“压路机－土”振动系统中，参与振动的除振动轮外，还包括随振动轮振动的一部分土。因此振动马达承受的负载是压路机振动轮与振动土共同作用的结果。压路机振动轮的质量在振动压实的过程中是不变的，但是振动土的质量与土的密度及内摩擦角等因素有关。由于振动压实中土体参数是动态变化的，具有随机性，因此振动土的质量也是随机变化的。这造成压路机振动负荷的波动。振动负荷的波动通过液压系统传递到发动机，造成发动机转速不稳定，最终影响振动频率的稳定性［4－8］。

闭环控制是摊铺机行走系统中常见的控制形式［9］，能够保证摊铺机在外界负载变化时仍以较恒定的速度前进［10］。因此从理论上讲，闭环控制是一种实现压路机振动频率稳定的较为理想的控制方式。为了验证闭环控制振动土频率稳定性的效果，采用试验及仿真的方法进行研究。

1 压路机振动液压系统分析

图1为典型的压路机振动液压系统原理图。振动泵由发动机进行驱动，带动振动马达产生力矩和速度，驱动钢轮产生振动。根据振动液压系统流量的连续性［11］，有

式中 np为振动泵输出转速，r/min;qp为振动泵排量，mL/r;ηpL为振动泵容积效率;nm为振动马达转速，r/min;qm为振动马达排量，mL/r;ηmL为振动马达容积效率。

由式(1)可得振动液压系统的减速比i为

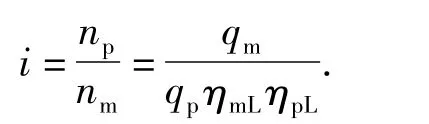
当振动马达所受的振动扭矩变化量为ΔM时，作用在发动机动力输出轴上的扭矩变化量ΔM1为

假设该过程中发动机始终处于调速段工作，且发动机调速段的扭矩—转速特性曲线表达式为

图1 单钢轮压路机振动液压系统原理图

式中 M1为发动机输入扭矩，N·m;k为发动机调速段扭矩—转速特性曲线斜率;b为该曲线在扭矩轴的截距。k、b取决于发动机本身的特性。

当发动机负载扭矩变化ΔM1时，引起的输出转速波动 Δnp为

联立式(2)、(3)得

该转速波动经振动液压系统传递到振动马达输出轴上，造成的振动马达输出转速波动量Δnm为

分析式(4)可知:1)减小负载扭矩的变化量，可以提高振动频率的稳定性。但是负载扭矩的波动是由被压实介质的不均匀特性决定的，无法进行人为控制。2)降低振动泵的排量，提高振动马达的排量，可以在一定程度上抑制振动频率的波动变化，但这样改变了整个振动液压系统的工作参数，不能获得理想的效果。3)改善发动机的调速特性，选用刚度较大的发动机，可以改善振动频率的不稳定现象，但会造成发动机功率的浪费。

当压路机振动系统正常工作时，其振动泵、振动马达的排量是不变的，此时振动马达转速的变化与负载扭矩变化成反比。当振动负载增大时，振动马达转速会降低，从而使振动频率降低。若在振动负载增大的过程中，相应减小振动泵的排量，则在一定程度上会增大振动频率的稳定性，这是闭环控制在振动液压系统应用中的思路［12－13］。

2 振动液压系统的闭环控制仿真

2.1 仿真模型的建立

为了研究压路机振动工作过程中负载变化对振动频率的影响，以某国产20 t单钢轮振动压路机作为试验样机，在室内土槽中进行低频高幅模拟压实试验。试验过程中利用数据采集仪对发动机转速、振动系统压力、振动马达转速等参数进行记录，对试验数据进行处理，得到压实过程中振动负载随时间的变化规律，如图2、3所示。

由图2可以看出，压路机在实际压实过程中，振动系统高压腔压力处于不断变化之中，低压腔压力基本维持不变。在给定的时间段内高压腔压力波动约为8 MPa，这是由于外界负载的波动引起的。由图3可以看出，由于振动系统压力的波动变化，导致加载到发动机输出轴上的外负载时刻处于变化之中，导致发动机转速波动，该时间段内发动机转速波动约为80 r/min。发动机转速波动引起振动马达转速波动，波动转速约为60 r/min，最终导致振动频率存在1 Hz左右的波动。

为了分析外界负载波动对振动频率的影响，运用AMESim软件对压路机振动系统进行建模。根据试验样机的基本参数，将变量泵的最大排量设定为45 mL/r，定量泵的排量设定为17 mL/r，定量马达的排量设定为55 mL/r。

为了简化模型，不考虑行走负载波动对发动机转速的影响，同时将发动机外特性曲线简化为线性模型，得到的模型如图4所示。

图2 振动系统压力变化

图3 发动机及振动马达转速变化

图4 振动液压系统仿真图

将试验数据导入到AMESim模型中，得到各参数的变化规律如图5所示。

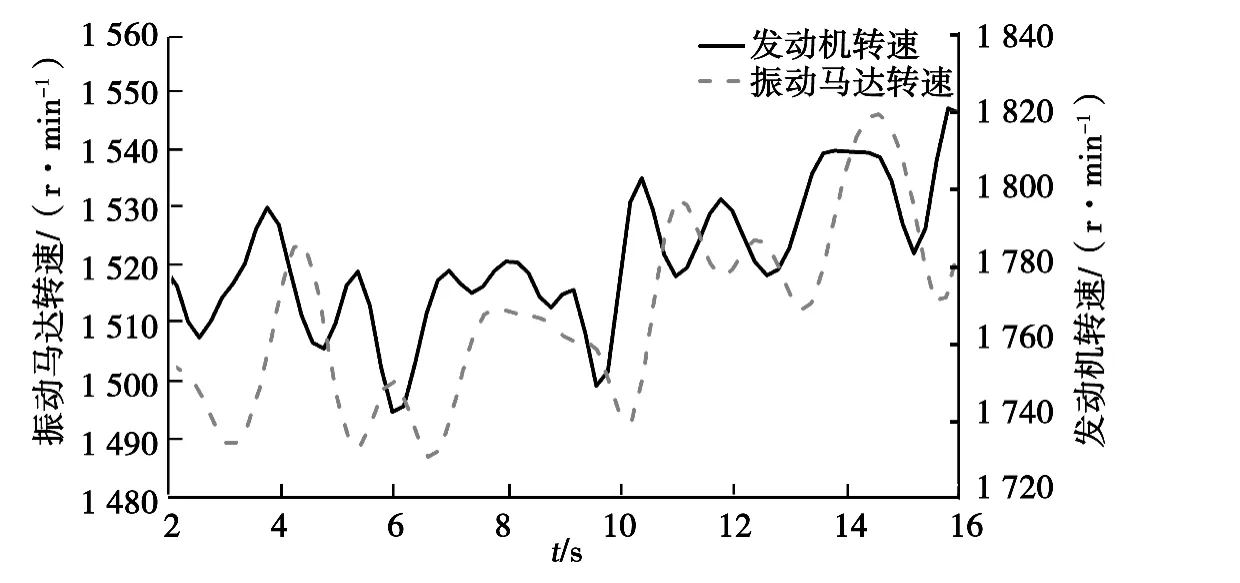
图5 发动机、振动马达转速仿真结果

对比图3、5可知，仿真结果与试验结果一致，说明仿真模型基本正确。利用闭环反馈的控制思想对现有振动液压系统模型进行改进。对比现有的液压系统闭环控制的方法，最终采用PID控制这一经典的控制方法［14］。

PID控制器是一种线性控制器，根据给定值与实际输出值构成控制偏差，将偏差的比例、微分、积分通过线性组合形成控制量，对被控对象进行控制［15］。对于试验样机的振动液压系统，为了实现振动频率的稳定性，需要检测振动马达输出转速，将被测转速与目标转速进行对比，并对差值信号进行PID运算，最终得到合理的电液伺服阀控制信号，控制振动泵排量发生改变，进而使被测转速趋于目标转速。系统方框图如图6所示。

通过添加PID模块，调整模块中各参数的取值，最终优化后的闭环控制振动液压系统模型见图7。

图6 振动液压系统PID控制方框图

图7 闭环控制振动液压系统仿真模型

2.2 仿真分析

通过调整PID模块中相应参数，当输入相同的振动负载时，最终得到的发动机转速特性曲线及振动马达转速变化曲线如图8、9所示。

图8 发动机转速仿真特性曲线

图9 振动马达转速仿真特性曲线

由图8可以看出，与改进前相比，加入闭环控制后，在相同的振动负载下，发动机转速的波动略有降低。这是因为在闭环控制系统的作用下，振动泵的排量依照被测转速的大小不断波动变化，导致实际加载到发动机动力输出轴上的负荷有所降低，因而发动机表现出来的速度波动减小。由图9可以看出，利用闭环反馈，振动马达的转速波动由原来的60 r/min降低至30 r/min，振动频率的稳定性有所提高，这一方面是由于发动机速度波动的降低引起的，另一方面也是由于振动泵排量的变化导致整个振动液压系统的减速比处于动态变化之中，从而使振动马达的转速波动有所减少。

3 结语

振动频率稳定性是保证压路机工作质量的重要参数，降低外界负载的波动、改善振动液压系统的工作参数、提高发动机速度刚度、采用闭环控制等可以提高振动频率的稳定性，采用闭环控制是一种较好的解决办法。通过对试验样机进行试验，并利用AMESim软件对振动液压系统进行闭环改造，能够在一定程度上提高压路机振动频率的稳定性。

［1］赵丽萍，李雨，沈建军.双钢轮振动压路机行走系统速度刚度研究［J］.山东交通学院学报，2013，21(3):76－79.

［2］龚创先.振动压路机压实性能研究与优化［D］.湘潭:湘潭大学，2013.

［3］张奕，龙水根.振动压路机振动频率恒定控制［J］.中国工程机械学报，2003，1(1):72－76.

［4］宁鹏，张敏，魏文澜.振动压路机振幅的探讨［J］.山东交通学院学报，2012，20(4):75 －77.

［5］张青哲，杨人凤，戴经梁.振动压路机——土壤系统动力学模型及分析［J］.建筑机械，2009(21):98－101.

［6］张泓，闻邦椿.振动压路机压实机理的研究［J］.建筑机械，2000(03)25－27.

［7］曹婷，胡碧阳，张志峰，等.双钢轮振动压路机动态负荷特性分析［J］.山东交通学院学报，2012，20(3):72－76.

［8］李军，李言，周志立.振动压路机振动频率控制系统研究［J］.机械科学与技术，2012，31(4):669－673.

［9］拾方治.沥青混凝土摊铺机行驶系统PLC控制技术研究［D］.西安:长安大学，2002.

［10］付辰琦.摊铺机行走速度平稳性控制的研究［D］.秦皇岛:燕山大学，2012.

［11］王静，秦文波，龚国芳，等.大流量高性能液压系统的若干关键技术研究［J］.浙江大学学报:工学版，2009，43(7):1264－1268.

［12］马鹏宇，胡永彪，张忠海.功率控制对外负荷在发动机调速特性上配置的影响［J］.筑路机械与施工机械化，2010(7):73－75.

［13］刘辉.履带式摊铺机行驶控制系统研究［D］.成都:西南交通大学，2012.

［14］张奕，申晓龙，刘桦.智能压路机振频控制系统的模糊自适应PID控制［J］.筑路机械与施工机械化，2006(8):48－50.

［15］王述彦，师宇，冯忠绪.基于模糊PID控制器的控制方法研究［J］.机械科学与技术，2011，30(1):166－172.