接近凸双调和多项式的构造
乔金静,高红亚
(河北大学数学与计算机学院,河北保定 071002)
接近凸双调和多项式的构造
乔金静,高红亚
(河北大学数学与计算机学院,河北保定 071002)
主要介绍单位圆盘上一类保向接近凸的双调和多项式.令上述双调和多项式的次数趋于无穷,取极限,进而得到一类接近凸的双调和映射.
双调和映射;接近凸;双调和多项式
MSC2010:30C45
解析函数是复分析中的主要研究对象.作为解析函数的推广,复平面上的调和映射也越来越得到人们的关注.而作为调和映射的推广,双调和映射来源于许多物理问题,特别是流体力学和弹性问题,它在工程学和生物学都有许多重要的应用[13],故它的研究具有明显的应用特色.本文主要研究单位圆盘上的双调和映射.
单叶(解析)多项式在验证几何函数论中的诸多猜测中发挥了作用,构造此类多项式的方法是经典的.而构造调和多项式和双调和多项式的相关文献很少.多项式的单叶性与其零点的位置关系密切.文献[4]考虑了调和多项式解析部分的导数Q在单位圆盘无零点的情形,给出了一类保向的调和多项式.如果进一步规定该导数Q的零点都在单位圆周上,可得一类接近凸的调和多项式[5].本文的主要目的是把上述结果推广到双调和映射的情形,构造一类接近凸的双调和多项式.
1 预备知识
设f是定义在单位圆盘D={z:|z|<1}上的复值调和函数,则f可表示为f=h+g,其中h,g在D上
解析.调和映射f局部单叶且保向的充分必要条件是JacobJf(z)是正的[67],其中
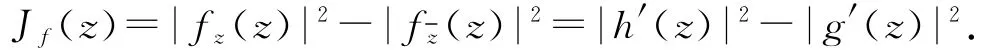
单位圆盘D上的4次连续可微函数F是双调和的当且仅当ΔF是调和的,即Δ(ΔF)=0,且双调和映射F具有表达式其中G和H是D上的复值调和映射.如果对于z∈D/{0},F的Jacob

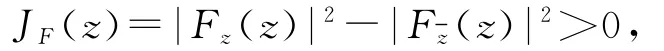
就称双调和映射F是保向的[89].
在文献[8,10]中,作者讨论了形如式(1)的双调和映射的性质,如单叶性和星形性,这里H(z)≡0.从而引出了形如F=|z|2G的单叶保向的双调和映射类.本文讨论形如F=|z|2G的双调和映射.
如果区域Ω的补集可以由闭的半直线覆盖,这里闭的半直线对应的开的半直线是不相交的,就称区域Ω是接近凸的.如果单叶双调和映射(或调和映射)映D到一个接近凸区域,就称此双调和映射(或调和映射)是接近凸的.
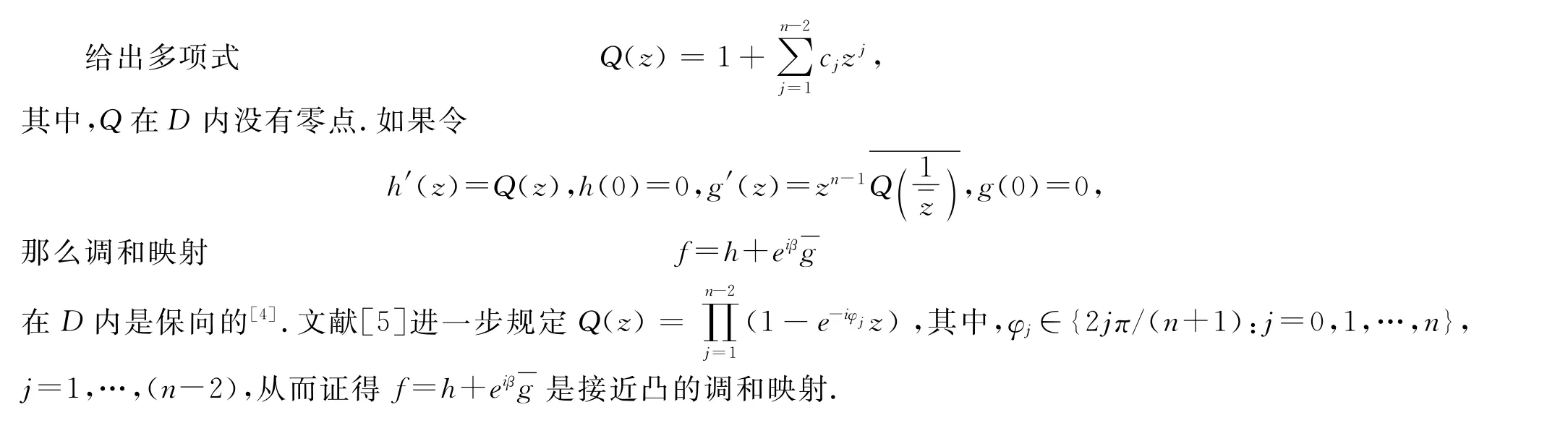
2 主要结果



[1] HAPPEL J,BRENNER H.Low reynolds numbers Hydrodynamics[M].Englewood Cliffs:Princeton-Hall,1965.
[2] KHURI S A.Biorthogonal series solution of Stokes flow problems in sectorial regions[J].SIAMJ Appl Math,1996,56:19 39.
[3] LANGLOIS W E.Slow viscous flow[M].New York:Macmillan Company,1964.
[4] SUFFRIDGE T J.Harmonic univalent polynomials[J].Complex Variables Theory Appl,1998,35:93 -107.
[5] JAHANGIRI J M,MORGAN C J,SUFFRIDGE T J.Construction of close-to-convex harmonic polynomials[J].Complex Var Theory Appl,2001,45:319 326.
[6] CLUNIE J G,SHEIL-SMALL T.Harmonic univalent functions[J].Ann Acad Sci Fenn Ser A I,1984,9:3 25.
[7] DUREN P.Harmonic mappings in the plane[M].Newyork:Cambridge Univ Press,2004.
[8] ABDULHADI Z,ABU MUHANNA Y,KHOURY S.On univalent solutions of the biharmonic equations[J].J Iequal Appl,2005,5:469 478.
[9] ABDULHADI Z,ABU MUHANNA Y KHOURY S.On some properties of solutions of the biharmonic equation[J].Appl Math Comput,2006,177:346 351.
[10] ABU MUHANNA Y.On univalence of biharmonic maps[J].Complex Var Elliptic Equ,2008,53:745 -751.
[11] PONNUSAMY S,QIAO Jinjing.Polynomial approximation of certain biharmonic mappings[J].Nonlinear Analysis,2012,81:149 158.
[12] SHEIL-SMALL T.Complex Polynomials[M].NewYork:Cambridge University Press,2002.
[13] KAPLAN W.Close-to-convex schlicht functions[J].Michigan Math J,1952,1:169 185.
[14] JAHANGIRI J M.A gap condition for the zeros of certain polynomials in Kaplan classes[J].Mathematica,1987,34:53 -63.
(责任编辑:王兰英)
Construction of certain close-to-convex biharmonic polynomials
QIAO Jinjing,GAO Hongya
(College of Mathematics and Computer Science,Hebei University,Baoding 071002,China)
A family of sense-preserving biharmonic polynomials that are close-to-convex on the unit disk is introduced.By taking limits as the degree of the polynomials tends to infinity,a family of close-toconvex biharmonic mappings is also obtained.
biharmonic mapping;close-to-convexity;biharmonic polynomial
O174
A
1000 -1565(2014)05 -0467 04
10.3969/j.issn.1000 -1565.2014.05.004
2013 06 -20
河北省自然科学基金青年科学基金资助项目(A2013201104)
乔金静(1980-),女,河北馆陶人,河北大学讲师,博士,主要从事函数论研究.E-mail:mathqiao@126.com

