液体火箭发动机氢燃料涡轮三维非定常流场数值研究

王朝晖，叶小明

（北京航天动力研究所，北京100076）

0 引言

众所周知，涡轮内部流动的本质是非定常的，包含了诸如尾迹、激波、泄露涡、二次流等多种复杂的非定常现象。而当前的涡轮设计体系基本上都是基于定常假设，无法捕捉到内部复杂的非定常流动现象，也就无法更清晰地揭示涡轮内部的流动机理。随着航空航天以及能源工业的快速发展，对涡轮性能的要求也越来越高，某些情况下，先前的定常假设体系已经略显欠缺，有必要开展非定常流动现象的研究，期望在深入理解非定常流动机理的基础上进一步提高涡轮的性能。

早在20世纪80年代，国外就开始了叶轮机械非定常现象的研究，到现在已经有许多学者对动静叶排干涉、叶片非定常力等非定常问题做了大量有价值的研究工作。Dring等人在1982年的研究表明，当静子和转子之间间距为15%平均轴向弦长时，转子前缘的非定常压力脉动可高达相对动压的80%左右[1]，这意味着它在叶片表面会产生很大的非定常载荷，这对叶轮机的性能、叶片强度等都会产生非常大的影响。1987年Giles用Lax-Wendroff时间推进格式求解了非定常欧拉方程组，分析了尾迹/转子之间的干涉效应，定性地预测了气动噪声和叶片非定常压力的产生[2]。1993年Aronoe用完全多重网格技术计算了转子叶排间的流动[3]。此外，国内方面也有学者对叶轮机械的非定常现象进行了一系列的研究[4-6]。

液体火箭发动机涡轮的特点是小尺寸、小流量、高转速、高压力（可达几十兆帕）、小展弦比和无冷却，与航空发动机用的大展弦比、大流量的涡轮有着明显的差别。过去众多学者的研究大都集中在航空发动机涡轮或燃气轮机，不论是设计、优化还是内部流动现象，对液体火箭发动机涡轮的研究并不多见，尤其对液体火箭发动机涡轮的非定常流动现象的研究更加少见。本文基于液体火箭发动机涡轮这个新的平台，对其非定常流动现象进行深入的研究与分析。

1 计算网格

为了适应叶片通道空间拓扑结构并保证较高的网格质量，对计算域采用多块结构化网格技术。建立涡轮模型时考虑了轮缘轮毂处的加工倒角，考虑了密封，网格最小正交角度21°。表1给出了计算网格分布情况，图1给出了子午流面网格划分和密封位置网格的局部放大图。图2给出了计算结果得到壁面y+分布云图，可见壁面y+最大值小于10，与所选用的Spalart-Allmaras湍流模型相一致。

表1 计算网格分布Tab.1 Distribution of computational grid

图1 子午流面网格划分图Fig.1 Grid generation on meridional stream surface

图2 壁面y+分布云图Fig.2 Distribution of y+at wall

2 求解方法

定常计算采用混合平面法，周向平均混合。非定常计算采用滑移面方法，交界面线性插值。本算例涡轮叶片数是23，50，31，48，为了减少非定常计算量，采用1989年Rai提出的区域缩放法[7]对转静子叶片数进行适当的调整，调整后为25，50，25，50，约化为1:2:1:2，调整叶片数的同时对叶型进行相应比例的缩放，以保证节弦比和堵塞度不变。

物理时间步长的选择起着非常重要的作用，在求解非定常流动情况时，时间步长太小，会使得计算量变大，推进时间变长，物理时间步长过大，又会导致不能捕捉到所关心变量的准确的变化情况，因此合适的物理时间步长是非定常计算中一个非常重要的参数。在叶轮机的非定常计算中，一般每个动叶栅距至少取10个物理时间步长以上。把动叶转过一个静叶栅距的时间定义为一个计算周期T，每个计算周期T选取20个计算点，计算25个周期，共500个物理时间步。

本算例为亚声速流动情况，进口给定气流总温、总压，轴向进气，出口给定静压，壁面条件绝热、无滑移。工质选用气态H2，cp=15 850 J/(kg·K)，γ=1.384，给出粘性系数随温度的变化曲线。湍流模型选择鲁棒性较好且收敛速度较快的Spalart-Allmaras模型。非定常计算采用Jameson提出的隐式双重时间推进法[8]，并结合多重网格法、当地时间步长和隐式残差光顺等加速收敛技术。空间离散采用二阶中心差分，并添加二阶和四阶人工粘性项。虚拟时间推进采用四阶龙格-库塔方法，每个虚拟时间步内均迭代计算50步。在进行非定常计算之前先进行定常求解，然后把定常计算的结果作为非定常计算的初始解。

为了验证网格无关性，在进行非定常计算之前先对不同数量的网格进行稳态计算，对比网格数量和计算效率的变化趋势。发现当网格数达到182万时，效率值基本无变化，所以接下来的计算都采用这一数量的网格进行。

3 结果分析

3.1 定常与非定常总体性能参数比较

为了了解模化（即叶片数和相应叶型的调整）对计算结果的影响，把模化前后的叶型都进行了定常计算。原始叶型的定常计算结果、模化叶型的定常和非定常时均结果的对比见表2。

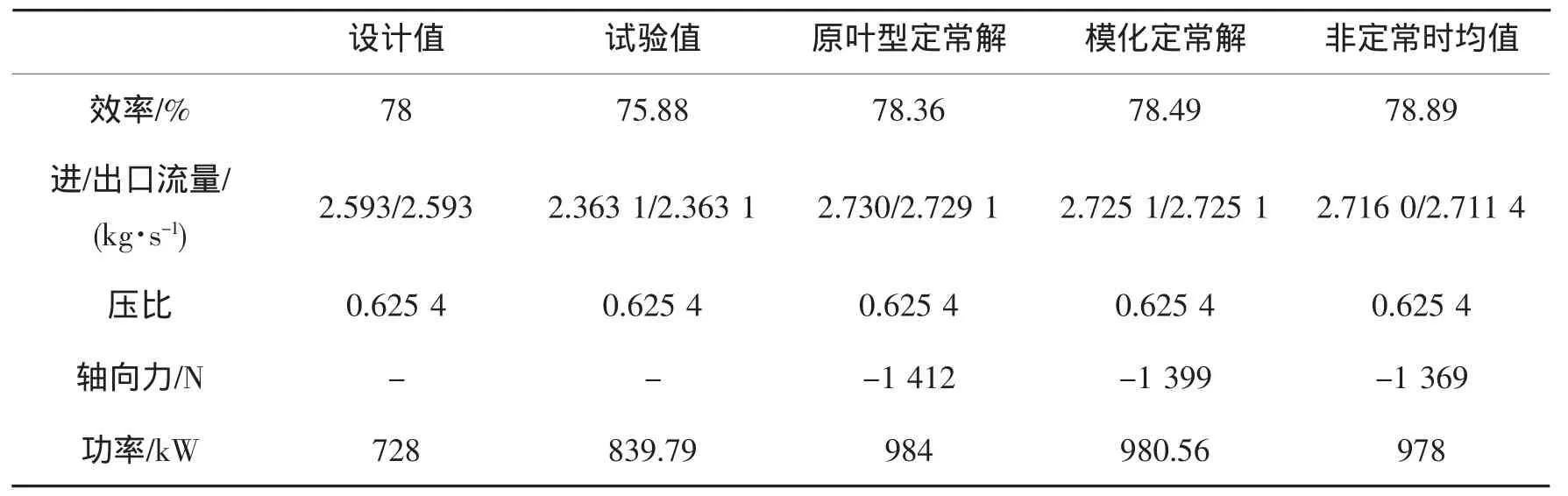
表2 定常和非定常结果比较Tab.2 Comparison of steady and unsteady results

比较模化前后的定常结果可以看出，在压比相同的情况下，模化后效率增加了0.13%，流量减小了0.18%，功率减小了0.4%，所有变化都小于0.5%。总体而言，所作的叶片模化对涡轮的数值模拟结果的影响很小，基本可以忽略，可以认为所作的模化是合理的。

下面着重对比分析模化后定常与非定常计算结果的差别。表2显示，模化后定常计算的质量流量结果比非定常稍大，但都高于设计值。非定常时均效率要比定常结果高出0.4个百分点，这是因为定常计算在动静交界面采用了周向平均模型，使本来不均匀的叶片排出口流场人为地混合均匀，增加了掺混损失。此外定常计算的流量高于非定常的结果，这主要是因为相同的出口背压下，非定常出口尾迹的低能流体流到后面的通道，使之产生了一定程度的堵塞，流量降低，使得前排叶栅进口气流攻角增大，进一步降低了流量，而定常计算情况下相应的通流能力较强。上述对比说明定常计算的结果只能是一定程度的近似，并不能真正反映涡轮的性能，想要得到涡轮的真实流动情况，还需要对其进行非定常计算。涡轮试验是在西安交大叶轮机械研究所微燃机涡轮试验台上进行的，试验涡轮为真实产品即模化前涡轮，由于试验台很难达到设计的高入口压力，因此涡轮试验是依据相似理论采用的模化试验。图3给出了涡轮性能参数试验结果与数值结果的对比。

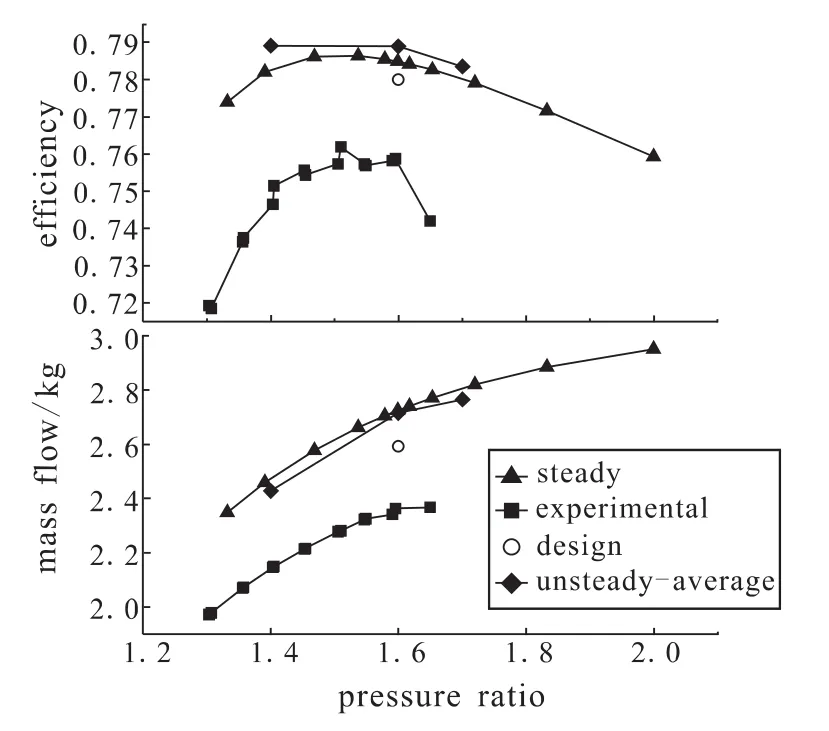
图3 性能曲线Fig.3 Performance curves

通过改变涡轮出口压力，计算了设计工况点之外的10个工况点。对图3给出的效率特性曲线对比分析，发现试验结果显示最高效率为75.88%，出现在设计点（即落压比1.6） 处。对比定常效率和试验效率，定常效率比试验效率要高出约2个百分点，这是由于数值计算简化了密封模型，认为工质为理想气体，因此得出的结果比试验值大。不论是试验结果还是数值结果，在额定转速下涡轮效率随落压比均变化缓慢，且均维持在较高水平，说明该涡轮实际运行性能较好，在设计工况下具有良好的气动性能表现。另外，从图3还可以看出，在设计点工况，定常和非定常结果差别很小；在偏离设计点工况，定常和非定常之间的差别开始变得明显。

分析图3给出的质量流量随落压比变化曲线对比情况，发现数值计算结果和原设计值均比试验结果大，这是因为涡轮试验是一个模化试验，试验涡轮本身的流量及功率就非常小，轴系摩擦等阻力因素占的比重相对较大，在性能参数结果的后处理时相对保守而且存在一定的试验误差所致。定常和非定常结果非常接近，尤其在设计点处两者差别非常小，在偏离设计点时开始稍有差别。从曲线的趋势来看，不论是数值结果还是试验结果，质量流量都是随着落压比变大而增加且增加趋势逐渐变缓并趋于稳定值。这不难从理论上解释，涡轮几何形状不变，进口总温总压不变，随着出口压力的减小，一级静叶流速增加，流量变大，在还未达到临界状态前，流量随着出口压力的降低而增加，当达到或超过临界状态后，不论如何降低出口压力，涡轮的流量都维持不变。

3.2 叶片表面非定常力分析

选取计算物理时间步的最后400步，得到监测点的压力随时间变化情况。一级静叶后缘吸力面一点（相对轴向弦长85%处，50%span） 压力随计算时间步的变化曲线如图4所示，快速傅里叶变换得到频谱图5。

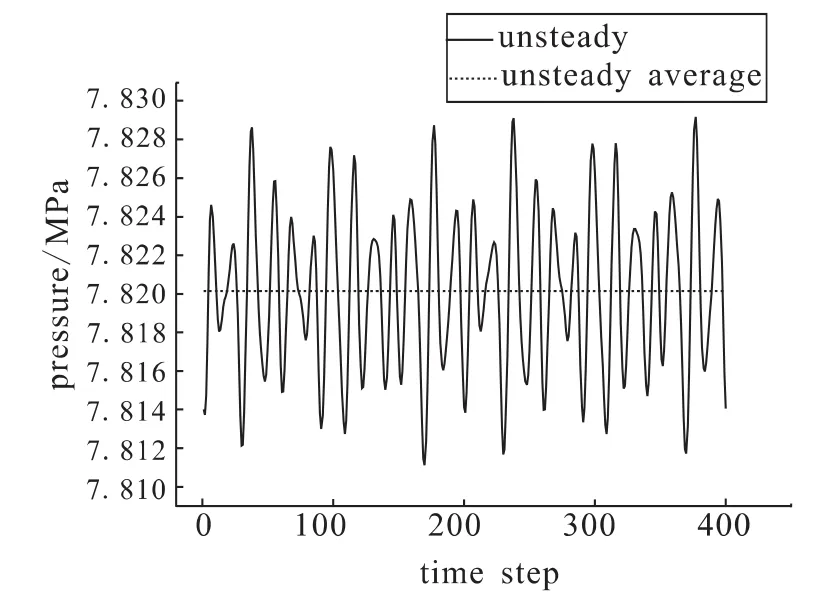
图4 一级静叶吸力面某点压力变化曲线Fig.4 Static pressure at a point on suction surface of first-stage static stator

从图5可以看出最大振幅对应频率为37 916.67 Hz，幅值4.5 kPa，除以当地压力平均值，波动百分比为0.57%。这说明一级静叶的流动还是比较稳定的，没有出现明显的非定常波动，静叶尾缘部分的微小波动主要是因为受到了交界面下游动叶前缘附近的势流场影响。从图5中可以看到有4个峰值频率，其中29 166.67 Hz和58 333.33 Hz的波动分别是由静叶排和动叶排的周期性排列引起的，其余的峰值频率明显是由动静叶排间相互干涉、叶排尾迹的非定常变化以及诸如二次涡流等非定常因素引起的。这些频谱信息只有在非定常计算中才可能得到，在定常计算中是不能获得这些频谱信息的。

图5 频谱图Fig.5 Distribution of frequencies

图6 给出了一级动叶吸力面前缘某点（相对轴向弦长15%位置，50%span） 的压力随计算时间步的变化情况。可以看到，该点的压力呈现出明显的周期性波动，并且呈现出类似谐波函数的变化特点，说明非定常计算可以反映出涡轮内部真实的流动情况。压力最大值与最小值相差约90 kPa，波动范围达1.2%，表现出较强的非定常现象，说明叶片会受到非定常激振力。

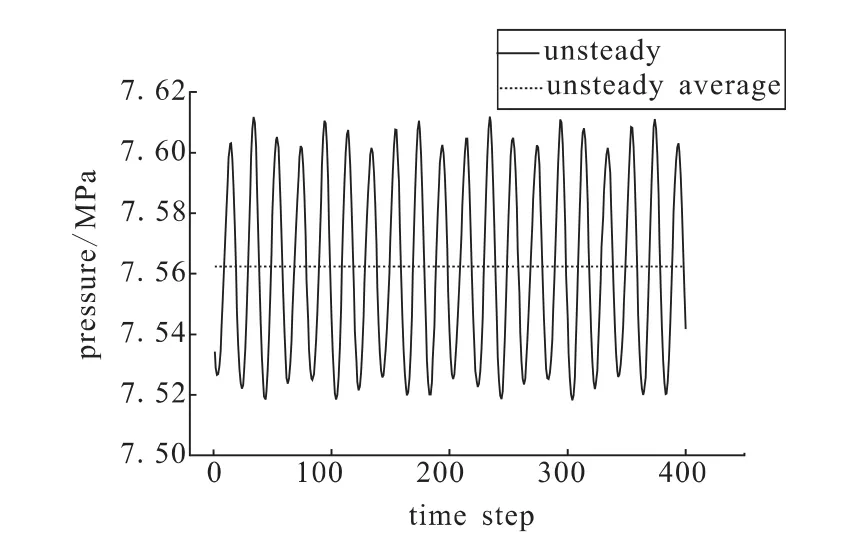
图6 一级动叶吸力面某点压力变化曲线Fig.6 Static pressure at a point on suction surface of first-stage moving rotor

对曲线进行快速傅里叶变换，得到该点静压的频谱图7，峰值频率为29 166.67 Hz，这与叶排通过频率BPF是相一致的。

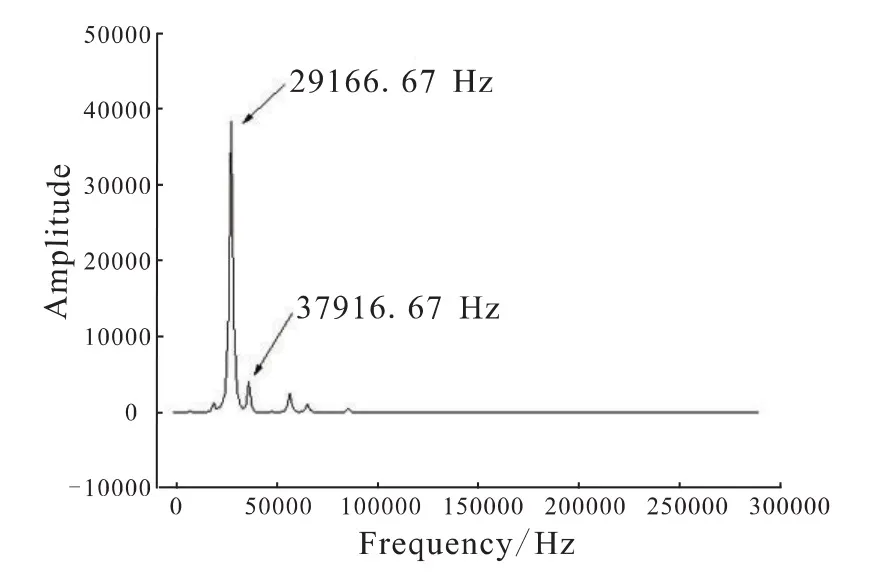
图7 频谱图Fig.7 Distribution of frequencies

在一级静叶和一级动叶排相互干扰中，叶排通过频率BPF与动静叶片数及动叶转速有关。叶排通过频率BPF是一片动叶通过一个静叶通道所需要时间的倒数：

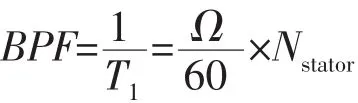
式中：Nstator为静叶排的叶片数；Ω为转速。按照原始的一级静叶数目23来说，计算可得叶片通过频率BPF=26 833.33 Hz，这与频谱图上的峰值频率并不吻合，两者之间相差约2 300 Hz。这是因为在计算过程中人为更改了一级静叶叶片数目，由23改为了25，同时对一级静叶进行了缩放，由此造成了流动参数频谱的移动。从上述结果可以说明，区域缩放法虽然可以在很大程度上减少计算量，但是由于人为地改变了叶片数目，将会导致流动参数频谱的微小移动，因此在利用区域缩放法研究叶片非定常气动力、叶片疲劳和叶片颤振等方面的问题时，需要注意缩放前后相应流动参数对应频谱图的微小偏移。

叶片力定义为叶片吸力面和压力面所受到压力引起的合力，叶片力除以平均值得到叶片力系数。图8描绘了一级动叶叶片力围绕其平均值的波动情况，由于动静叶排的相对周向运动，前排尾迹周期性地扫过动叶，尾迹与边界层的相互作用周期性地改变着动叶表面的压力分布情况，进而使得叶片受力也跟着发生周期性波动。

图8 一级动叶叶片力系数随时间变化曲线Fig.8 Variation of blade force coefficient of first-stage moving rotor with time

从图8可看出叶片力呈现类似简谐波的、显著的、有规律的周期性波动，叶片力围绕平均值的波动幅值达15.78%，波动的频率为29 166.67 Hz，和动叶片通过静叶栅距的频率相一致。

动叶叶片所受到的沿转轴方向的力矩直接决定着涡轮的做功能力。叶片力矩定义为叶片力周向分量对转轴的力矩，叶片力矩除以平均值得到叶片力矩系数。通过非定常计算考察动叶在旋转过程中所受到的沿转轴方向的力矩变化情况对理解和评估涡轮转子做功性能和稳定性等将是非常有帮助的。图9给出了一级动叶叶片力矩系数随时间变化曲线。

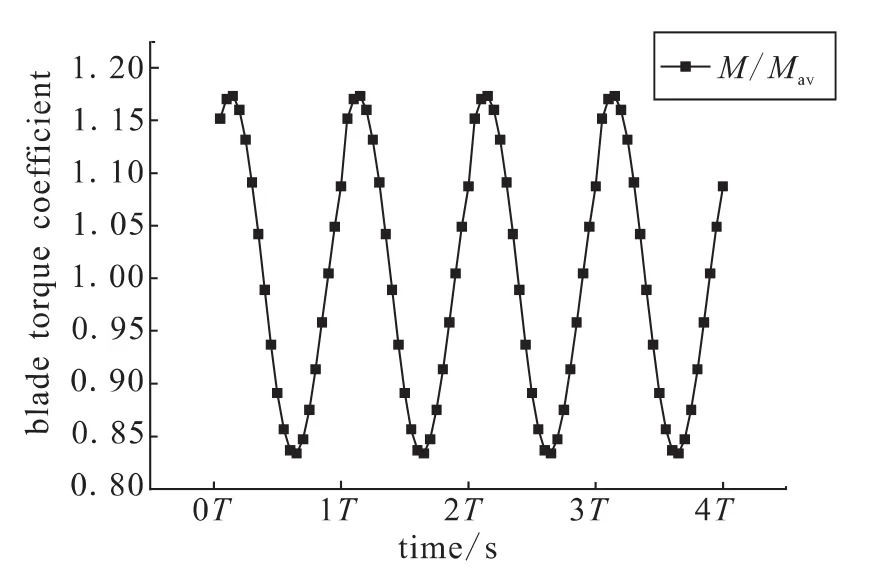
图9 一级动叶叶片力矩系数随时间变化曲线Fig.9 Variation of blade torque coefficients of first-stage moving rotor with time

从图9可见，力矩的变化趋势和叶片力的情况类似，波动幅值稍大一些，达到了17.31%。不论是力还是力矩的波动，都对涡轮整体性能有一定的影响，过于强烈的叶片力波动将会对叶片的强度和寿命造成影响，严重时可能造成叶片的损坏，不稳定的力矩会影响涡轮功率的稳定输出。

二级动叶吸力面某一点（相对轴向弦长15%处，50%span）压力变化情况如图10所示。频谱图如图11所示，频谱图上峰值频率29 166.67 Hz的波动源自二级静叶的影响。从波动曲线可以看到该点的最大静压差为88 kPa，波动幅值达1.44%。图12和图13给出了二级动叶叶片力和力矩系数的变化情况，可以看出，与一级动叶类似，力和力矩系数均呈现明显的规律性的周期性波动。二级动叶叶片力的大小变化幅度5.9%，二级动叶沿转轴方向的力矩波动幅值8.23%，波动频率为29 166.67 Hz，与动叶通过静叶栅距频率相一致。与一级动叶相比，二级动叶叶片力和力矩的波动幅值略小。

图10 二级动叶吸力面某点压力变化曲线Fig.10 Static pressure at a point on suction surface of second-stage moving rotor

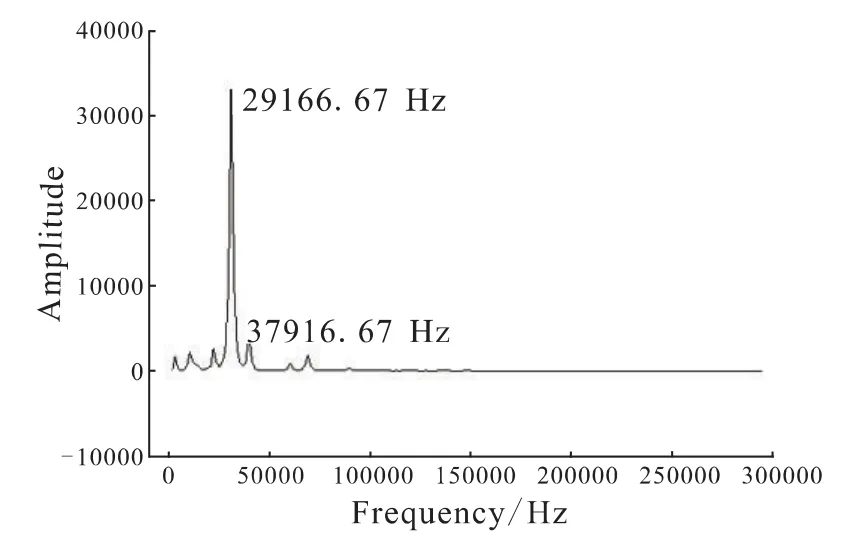
图11 频谱图Fig.11 Distribution of frequencies

图12 二级动叶叶片力系数随时间变化曲线Fig.12 Variation of blade force coefficient of second-stage moving rotor with time

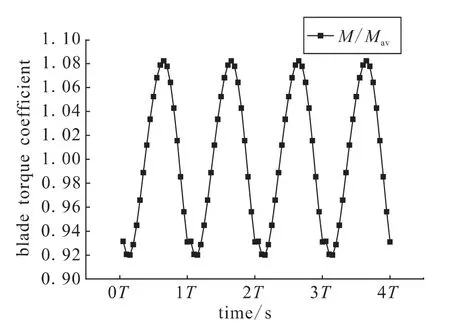
图13 二级动叶叶片力矩系数随时间变化曲线Fig.13 Variation of blade torque coefficients of second-stage moving rotor with time

通过分析可以发现本涡轮算例的叶片力和力矩的波动较为明显。不稳定现象产生的根源主要是涡轮内部存在着周向不均匀性以及由于端壁二次流、通道涡等因素。如何减小这种非定常因素是降低涡轮非定常叶片力和力矩的关键，由于本涡轮叶片叶高相对较小，属于小展弦比涡轮，因此端壁二次流在主流中所占的比重相对较大，可以考虑采用端壁筋方法抑制端壁二次流的产生和发展，即在叶栅通道的端壁面上沿流向设置一条高度和边界层厚度相当的细小的凸起，以阻止壁面边界层流体从压力面到吸力面的横向流动，达到减少端壁二次流的目的，从而减弱涡轮内部的非定常因素。另外，还可以充分论证各叶排间的轴向间距，筛选出最优的叶排轴向间距，也可以起到减弱涡轮非定常效应的作用。

叶片表面压力分布是衡量叶片气动性能的重要参数，它不仅决定了叶片作功能力，而且在一定程度上会影响叶片的强度和寿命等。一级动叶处于两排静子中间，受到尾迹与势流的双重干扰，非定常性较强。图14给出了各排叶片表面压力变化情况的对比。通过对比可见，一级动叶的压力波动幅度最显著，与上文结论一致。从图14（b）一级动叶的表面压力曲线可以看出，静子尾迹被转子叶片切割时，在一级动叶叶片前缘有较大幅度的压力扰动。这表明尾迹明显改变了来流气流角，导致一级动叶叶片前缘承受着较大幅度的非定常负荷。尾迹在向下游运动的过程中，对动叶吸力面的影响比对压力面的影响更为强烈，而且一级动叶吸力面的波动范围和波动幅度都比压力面更为强烈。虽然压力面在尾迹扫过时同样引起表面负荷波动，但相对于吸力面而言，其脉动幅度较小，主要是因为压力面前缘附近的逆压梯度小，大部分区域为顺压梯度，流动保持加速流动状态。这种情况下，边界层流动对外界扰动并不敏感，尾迹的影响相对较弱。

图14 一个计算周期T内叶片表面压力变化情况Fig.14 Pressure distribution on blade surface in one calculation period T

涡轮的另一个非常重要的非定常特性就是叶片进口气流角会发生周期性的变化，这主要是由于前排叶栅通道出来的不均匀流周期性地经过下游叶片入口所引起的。图15给出了中叶展截面动叶进口气流角的变化情况。

图15 不同时刻中叶展截面动叶进口气流角沿栅距的分布Fig.15 Distribution of inflow angle at mid-span section of rotor at different time

从图15可以看到，一级动叶进口气流角在一个周期内变化幅度大约为5°左右，二级动叶进口气流角波动幅度达10°左右。由此可见非定常因素在本算例中是非常明显的。

4 结论

通过对液体火箭发动机两级轴流氢燃料涡轮进行非定常数值模拟，着重分析了涡轮动静叶排干涉、非定常叶片力以及涡轮性能曲线等问题，得到以下结论：

1）区域缩放法可以有效地计算涡轮内部非定常流动现象，通过快速傅里叶变换可以获得到流场中压力波动的频谱信息。计算结果表明：本算例中一级动叶叶片力和力矩存在较大的非定常波动，波动幅值达15.78%和17.31%。

2）定常计算忽略了涡轮内部流动周向不均匀性等非定常因素，与真实流动情况有一定差别，不能捕捉到叶排间干涉和叶片非定常力等现象，无法更加准确全面地反映涡轮的性能。某些情况下，只有定常计算还不够，还需要对其进行非定常计算作为补充和校核。

3） 在非定常条件下，涡轮静子尾迹和位势作用将直接影响并改变下游动叶叶片表面负荷分布，特别是动叶前缘和吸力面扩压段等位置受到的影响更为强烈，从而对涡轮性能产生较为显著的影响。非定常因素导致了动叶进口气流角发生较大的波动，一级和二级动叶进口气流角波动范围分别可达5°和10°左右。

4） 就总体性能参数而言，在设计点工况，定常和非定常结果相差不大；在偏离设计点工况，差别开始变得稍加明显，而非定常结果更加符合实际情况。

[1]DRING R P,JOSLYN H D,HARDIN L W,et al.Turbine rotor-stator interaction,ASME 82-GT-3[R].USA:ASME,1982.

[2]GILES M B.Calculation of unsteady wake/rotor interactions,AIAA-87-0006[R].USA:AIAA,1987.

[3]ARONOE A.Viscous analysis of three-dimensional rotor flows using a multigrid method,NASA-TM-106266[R].USA:NASA,1993.

[4]邹正平,叶建,张永新,等.非定常流动对叶片表面负荷分布影响的数值模拟研究[J].燃气涡轮试验与研究,2006,19(1):21-26.

[5]祈明旭,丰镇平.动静干涉效应对轴流透平级气动性能的影响[J].工程热物理学报,2003,24(1):39-42.

[6]吴先鸿,陈懋章.非定常动静叶干涉作用的二维数值模拟[J].航空动力学报,1998,13(2):123-128.

[7]RAI M M.Three-dimensional Navier-Stokes simulations of turbine rotor-stator interaction:Methodology[J].Journal of Propulsion and Power,1989,5(3):305-311.

[8]JAMESON A.Time dependent calculations using multi-grid with applications to unsteady flows past airfoils and wings,AIAA 91-1596[R].USA:AIAA,1991.