一类奇异三阶两点边值问题正解的存在性

刘瑞宽

（西北师范大学数学与统计学院,甘肃 兰州730070）

1 预备知识

三阶微分方程在应用数学和物理等很多学科中有重要的应用,可以描述挠度弯曲的梁,有固定或改变交叉的部分,电磁波的传播和重力驱动等,见文献［1］.近年来,三阶边值问题已受到广泛关注［2-8］.其中,文献［2-3］中运用上下解方法研究了三阶边值问题正解的存在性,文献［5-9］通过降阶法和比较原理研究了三阶两点和多点边值问题正解的存在性.特别地,文献［10］运用Krasnoselskii's不动点定理研究了三阶奇异边值问题

正解的存在性与多解性.文献［11-12］通过讨论相应线性算子第一特征值,给出了三阶两点边值问题的正解存在性结果.受以上文献的启发,本文考虑三阶两点边值问题（1）正解的存在性,其中允许a（t）在t＝0或t＝1处有奇性.通过对相应线性算子第一特征值的讨论,运用不动点指数理论获得当f0、f0、f∞、f∞∈（0,+∞）时正解的存在性结果,对文献［9］结果进行了补充,并且本文得到的结果是最优的.

为了方便,记

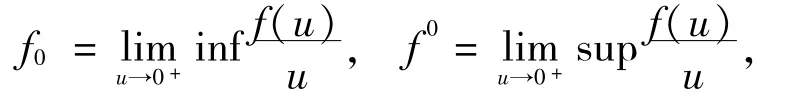
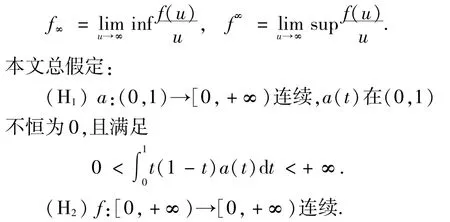
本文主要结果的证明基于下面的不动点指数理论.

定理1.1［13］设E是Banach空间,K⊂E为E中的一个锥.假设Ω为E中的有界开集,且T:K∩→K紧,则以下结论成立:

（i） 若存在 u0∈K＼｛θ｝,使得

u-Tu≠τ u0, u∈K∩∂Ω, τ≥0,则不动点指数i（T,K∩Ω,K）＝0.

（ii） 若 u≠τ Tu,u∈K∩∂Ω,τ≥1,则不动点指数 i（T,K∩Ω,K） ＝1.

本文的工作空间是 X:＝｛u∈C［0,1］:u（0）＝u′（0） ＝u″（1） ＝0｝,其在范数下构成 Banach空间.对于∀r＞0,令 Br＝｛u∈C［0,1］:‖u‖ ＜r｝,∂Br＝｛u∈C［0,1］:‖u‖ ＝r｝.定义X 中的锥 K ＝｛u∈X:u（t）≥0,t∈［0,1］｝,显然 K为X中的非负锥.为了得到更好的结果,对于∀0＜τ＜1,定义如下的锥

2 主要结果及证明

［1］ Greguš M.Third Order Linear Differential Equations［M］.Dordrecht:D Reidel Publishing Co,1987.

［2］ Cabada A.The method of lower and upper solution for third-order periodic boundary value problem ［J］.J Math Anal Appl,1995,195:568-589.

［3］ Cabada A.The method of lower and upper solution for second,thrid,fourth,and higher order boundary value problem ［J］.J Math Anal Appl,1994,185:302-320.

［4］ Agarwal R P,Bohner M,Wong P J Y.Positive solution and eigenvalues of conjugate boundary value problem ［J］.Proc Edinburgh Math Soc,1999,42:349-374.

［5］ Grossinho M R,Minhó s F.Existence result for some third order separated boundary value problems ［J］.Nonlinear Anal,2001,47:2407-2418.

［6］ Cabada A,Lois S.Existence of solution for discontinuous third order boundary value problems ［J］.J Comput Appl Math,1999,110:105-114.

［7］ Yao Q L.Successive iteration of positive solution for a discontinuous third-order boundary value problem ［J］.Comput Math Appl,2007,53:741-749.

［8］Cabada A,Heikkil¨a S.Extremality and comparison results for discontinuous third order functional initial-boundary value problems［J］.J Math Anal Appl,2001,255:195-212.

［9］ Jackson L K.Existence and uniqueness of solutions of boundary value problems for third order differential equations ［J］.J Diff Eqns,1993,13:432-437.

［10］ Li S H.Positive solutions of nonlinear singular thrid-order two-point boundary value problem ［J］.J Math Anal Appl,2006,323:413-425.

［11］ Liu Z Q,Sheok J U,Kang S M.Positive solutions of a singular nonlinear third order two-point boundary value problem［J］.J Math Anal Appl,2007,326:589-601.

［12］ Erbe L.Eigenvalue criteria for existence of positive solutions to nonlinear boundary value problems ［J］.Math Comput Model,2000,32:529-539.

［13］郭大钧.非线性泛函分析［M］.2版.济南:山东科学技术出版社,2001.

［14］ Zhang G W,Sun J X.Positive solutions of m-point boundary value problems［J］.J Math Anal Appl,2004,291:406-418.

［15］孙彦,刘立山.三阶奇异边值问题的正解［J］.应用数学学报,2009,23（1）:50-58.

［16］张立新.三阶边值问题的3个正解的存在性［J］.四川师范大学学报:自然科学版,2011,34（4）:466-470.

［17］ Ma R Y,Yang Y R.Existence result for s singular nonlinear boundary value problem at resonance ［J］.Nonlinear Anal,2008,66:671-680.

［18］刘兴元.具p-laplacian算子方程多点边值问题3个正解的存在性［J］.四川师范大学学报:自然科学版,2012,35（1）:78-81.

［19］马如云.二阶奇异边值问题的正解［J］.数学学报,1998,41（6）:1225-1230.

［20］ Asakawa H.Nonresonant singular two-point boundary value problems［J］.Nonlinear Anal,2001,44 （6）:791-809.

［21］ Yao Q L.Positive solutions and eigenvalue intervals of a singular third-order boundary value problem［J］.Ann Polon Math,2011,102（1）:25-37.

［22］ Yao Q L.Solvability of third-order three-point boundary value problems with Carathé odory nonlinearity［J］.Commun Math Res,2012,28（3）:209-217.

［23］王彦,姜杰,裴银淑.一类三阶微分方程的奇异非线性边值问题［J］.吉林大学学报:理学版,2003,41（3）:280-283.

［24］ Sun J P,Guo L J,Peng J G.Multiple nondecreasing positive solutions for a singular third-order three-point BVP［J］.Commun Appl Anal,2008,12（1）:91-100.

［25］ Hu L G.Positive solutions to singular third-order three-point boundary value problems on time scales［J］.Math Comput Model,2010,51（5）:606-615.

［26］ Feng X F,Feng H Y,Bai D L.Eigenvalue for a singular third-order three-point boundary value problem［J］.Appl Math Comput,2013,219（18）:9783-9790.

［27］ Liu Z S,Chen H B,Liu C.Positive solutions for singular third-order nonhomogeneous boundary value problems［J］.J Appl Math Comput,2012,38（1/2）:161-172.