双馈与直驱风电机组的小干扰稳定性对比分析*
李培强,王继飞,李欣然,郝元钊
(湖南大学 电气与信息工程学院,湖南 长沙 410082)
随着大规模电网的互联,由于弱联络线等引起的振荡问题不容忽视.伴随着可再生能源的开发与利用、越来越多的风电场接入电网的同时,对风电场接入电力系统后的影响进行分析研究成为电力系统急需解决的课题[1-9].大规模的风电场接入会对原有系统的振荡模式产生怎样的影响,阻尼比增大还是减小,风电场的接入是否利于系统的小干扰稳定等问题,都是需要进行深入研究的.不同的风电机组类型和容量比例对电网小干扰稳定性的影响可能是多样的.为了大规模利用风能,研究这些因素对电力系统静态稳定性的影响十分必要.
目前,国内外的专家学者针对并网型风力发电技术的各个方面进行了许多有意义的研究.文献[10]根据风电场不同容量下的系统稳定情况提出了风电场绝对安全容量的概念.文献[11]概述了目前投入市场的各种不同类型的风电机组,详细讨论了其不同的结构、原理以及彼此相应的对比.针对双馈型风力发电机组,文献[12]提出了利用暂态稳定指标η与极限切除时间CCT共同来评估系统的暂态稳定性.文献[13]基于功角和频率两种稳定判据,提出了一个在两种运行方式下,采用3种扰动方式的风电场极限穿透功率计算方法,并且通过仿真得到了影响该系统并网容量的主要因素是频率波动的结论.文献[14]介绍了双馈感应发电机与直驱同步发电机两种变速风机的数学模型,并通过比较模型对风速的响应数据与实际中测量的响应数据,证明了模型的可用性.但上述文献都没有针对不同类型风电机组对系统的小干扰稳定进行对比研究.
本文分析了2种风电机组的数学模型,通过强耦合两区域系统的算例,得出风机并网后,增加了系统的强相关的振荡模式,而对系统阻尼特性的改变不明显.当风电机组在系统中的容量提高时,系统原有的同步机组区间或局部振荡模式改变不大,而振荡特性有所变化,双馈机组穿透功率的增加会减弱新增局部振荡模式的阻尼,直驱机组穿透功率增加能提高区域内发生的与风电机组相关的局部振荡的阻尼.
1 风电机组的数学模型
1.1 双馈风电机组模型
双馈异步发电机的定子绕组与电网直接相连,转子绕组通过一个带有电流控制环的背靠背电压源换流器与电网相连,实现了转子的电气频率与机械频率解耦.换流器通过注入频率可变的转子电流来补偿机械频率与电气频率之差.如下式所示:

其中fs为定子输出频率;p为发电机极对数;fm为转子机械频率;fi为转子电流频率.通过控制转子的电流频率fi使得定子的输出频率fs保持恒定,从而实现风机的变速运行.
与恒速机组相比,双馈机组增加了转速控制模块、电压控制模块及桨距角控制模块.风速模块与恒速机组相同,减少了轴系模块.双馈机组的机械部分与电气部分基本上被换流器解耦,换流器的控制方式决定了轴系模型所反映的机端特性.由于换流器的动态过程相比于发电机电磁暂态过程要快的多,因此换流器用一个理想电流源等效代替.电流按d,q轴分解为iqr与idr,分别用于控制转速模块与电压模块.用下述方程描述:


流过换流器转子电流的限制是通过设置有功和无功功率限制值实现的.换流器是短路故障时双馈机组中最敏感的部件,因此必须对转速模块与电压模块加以限制,以避免暂态过电流的影响.方程如下所示:

桨距角控制模型由如下微分方程表示:
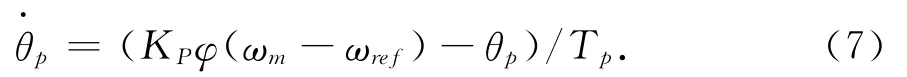
其中φ为桨距角起始改变设置点函数.桨距角控制只有在转速超过同步转速时才开始起作用.Tp为桨距角控制时间常数.
1.2 直驱风电机组模型
直驱同步机组的换流器与定子绕组相连,因此描述换流器的电流源电流分别为:iqs,ids与idc用于转速控制,无功控制以及电压控制,其控制方程为:
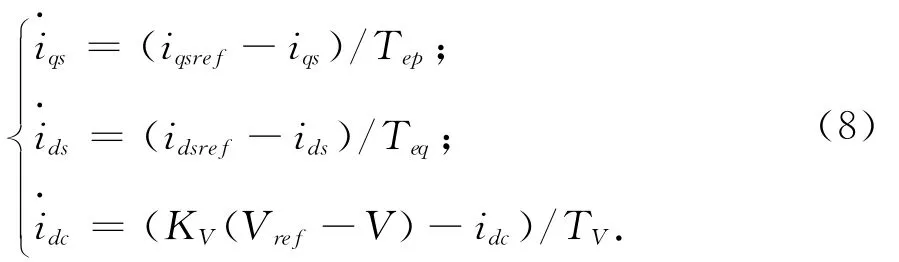
由此决定的电磁转矩及无功功率为:
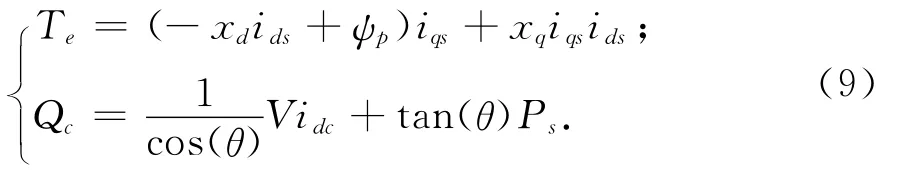
其中ψp表示永磁磁通量.保护系统对流过换流器的定子电流限制如下:
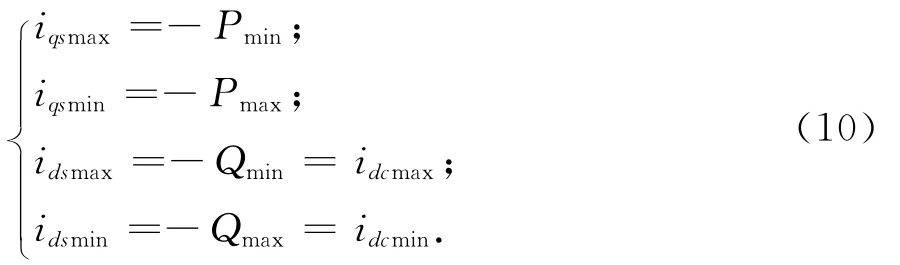
具体模型及其参数详见文献[9].
2 模态分析与参与因子
基于系统线性化模型的模态分析是目前电力系统小信号稳定分析中最成熟的一种方法.它能给出关键失稳模态、参与因子等重要信息,从而为抑制低频振荡提供理论指导.为确定模态与状态向量之间的关系,把左特征向量和右特征向量结合起来,确定度量模态与状态变量之间关联程度的参与因子矩阵P.矩阵元素Pij为参与因子,表示第j个模式与第i个状态变量的互相参与程度,即可观性,也包含了第i个状态变量对模式j的可控性信息.第i个状态变量对第j个特征值的参与因子可通过下式计算:

鉴于特征向量的规格化,与任何模式或任何状态变量相关的参与因子之和等于1.参与因子Pij越大表示参与程度越高,找出Pij最大的发电机组,就可判断它是否与该振荡模式强弱相关,从而为安装抑制该振荡模式的PSS电力系统稳定器或其他控制提供参考.
3 强耦合系统的两区域算例
为分析风力发电机组对电力系统特征值的影响,本文构建了如图1所示测试系统.它由两部分组成,一部分是大型强耦合系统,用无穷大母线表示,另一部分由两台同步发电机组成.为了考虑不同类型风电机组的影响,节点3的同步发电机分别由双馈机组以及直驱机组代替.阻抗以2 500MVA为基值的标幺值表示,负荷采用恒功率模型.发电机发出功率均为2 500MW,节点电压为1.025p.u..母线2与母线1的联络线阻抗为0.1+j1.0.母线2与母线3,4的联络线阻抗均为0.01+j0.1.频率为50 Hz,电压等级为220kV.
通过计算,共轭复数特征值与发电机转子运动方程对应,称为低频振荡模式,实部反映了低频振荡的衰减特性,虚部反映了低频振荡的频率,复特征值σ±jω所对应振荡模式的阻尼比和频率分别为与ω/2π.小扰动随时可能发生,且当系统阻尼比较弱时,都有可能造成系统动态失稳,通常要求系统正常运行下区域振荡模式的阻尼比不小于0.04.
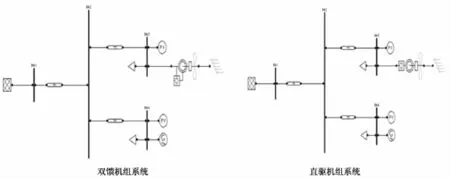
图1 用于小扰动分析的各机组系统Fig.1 Analyse system of wind pant to small distribution
双馈机组有11个特征值,2对共轭特征值,其频率与阻尼比如表1所示.直驱机组有11个特征值,2对共轭特征值,其频率与阻尼比如表2所示.各系统特征值的分布如图2所示.

表1 双馈机组系统的振荡模式Tab.1 Oscillation model of doubly fed induction generator
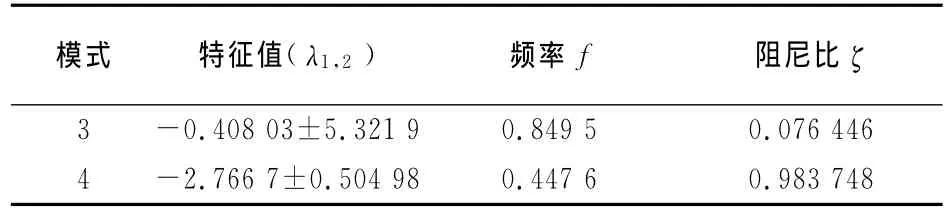
表2 直驱机组系统的振荡模式Tab.2 Oscillation model of direct drive synchronous generator
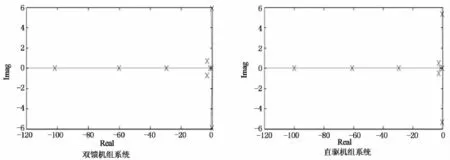
图2 各系统特征值分布对比图Fig.2 Equivalent value contrast of different system
将双馈机组替换母线3的同步发电机后,模式1与状态变量δ1,ω1的参与因子最大,均为0.467 4.模式2与状态变量e'd及idr的参与因子最大,分别为0.464 41,0.441 2,即主导因素是同步发电机的暂态电势d轴分量与双馈机组转子电流的d轴分量idr.
将直驱机组替换母线3的同步发电机后,模式3与状态变量δ1,ω1的参与因子最大,均为0.459 2.模式4与状态变量idc及e'd的参与因子最大,分别为0.481 21,0.436 35,即主导因素是直驱机组换流器电流的d轴分量idc与同步发电机的暂态电势d轴分量.
综上所述,在2种风电机组接入电力系统后,增加了与风电机组强相关的振荡模式,但这些振荡模式阻尼比较高,有很好的阻尼特性.风电机组替代同步机组接入后,虽然改变了系统的振荡模式,但是对系统阻尼特性的改变不明显.
4 不同风电机组容量对小干扰稳定的影响
为研究风电穿透功率对系统特征参数的影响,本文构建了如图3所示两区域系统.母线2处的同步发电机组逐步被风电机组取代.初始时3个PV节点发出的有功功率均为700MW.逐步增加风电机组出力,相应减少母线处并联同步机组的出力,分析风电功率增加对系统小干扰稳定的影响.风电机组的出力至100MW,200MW,300MW.相应母线12处的同步机组出力为600MW,500MW,400 MW,分析其振荡模式的变化.

图3 两区域系统Fig.3 Two area system
4.1 双馈机组情形
表3反映了含双馈机组系统的机电振荡模式.分析参与因子,模式1的最相关状态变量分别是1#机组与4#机组的δ与ω.模式2最相关的是2#机组与3#机组的δ与ω,以上两种模式均为局部振荡.模式3最相关的状态变量是3#机组与4#机组的δ与ω,为区间振荡模式.模式4最相关的状态变量是双馈机组的idr,说明该模式是与双馈机组相关的振荡模式.模式5与2#与3#同步机组的δ与ω的相关度较大,为新增的局部振荡模式.
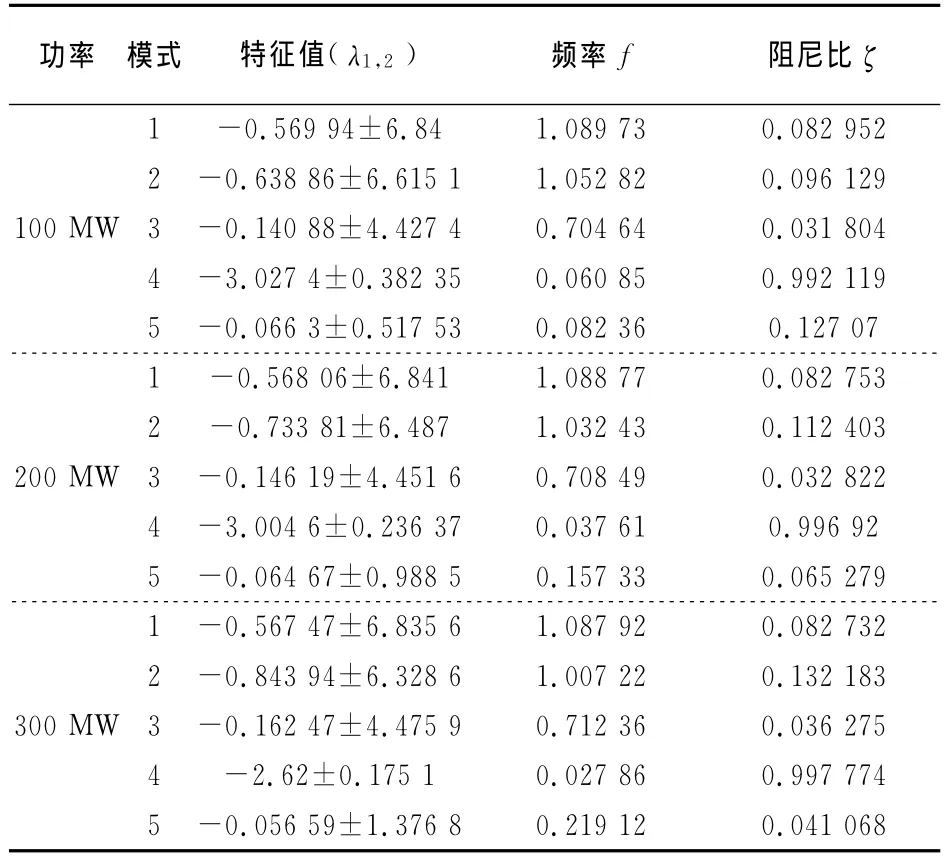
表3 双馈机组系统的振荡模式Tab.3 Oscillation model of doubly fed induction generator
表3反映了增加双馈机组出力后振荡模式的变化.由表可知,随着机组出力的增加,模式2与模式3的阻尼比稍有增加,模式1保持不变,模式5降低较大.说明双馈机组穿透功率的提高,不利于风机所在区域局部振荡的阻尼.而与风电机组相关的振荡模式4阻尼比变化不大,频率很低,具有良好的阻尼特性.
双馈机组系统前3种模式的阻尼特性差别不大.与风电机组相关的振荡模式具有更好的阻尼比,但却出现了一个风机所在区域局部振荡的模式,且随着风电穿透功率的增大,阻尼比减少较大.其原因是,双馈机组系统没有针对小干扰稳定的控制,即在系统发生振荡时,通过定子回路感知系统电气量的变化,从而在转子侧感应出振荡电流,产生出阻尼转矩.由于双馈机组内部电阻较小,阻尼转矩抑制振荡的能力较低,因此会导致系统阻尼降低.
4.2 直驱机组情形
表4反映了含直驱机组系统的机电振荡模式.分析参与因子,模式1的最相关状态变量分别是1#机组与4#机组的δ与ω.模式2最相关的是2#机组与3#机组的δ与ω,以上两种模式均为局部振荡.模式3最相关的状态变量是3#机组与4#机组的δ与ω,为区间振荡模式.以上与前两种机组系统相同.模式4最相关的状态变量是3#机组的δ,ω与直驱机组的idc,说明该模式是同步机组与直驱机组相关的局部振荡模式.

表4 直驱机组系统的振荡模式Tab.4 Oscillation model of direct drive synchronous generator
4.3 分析与讨论
1)风电机组在系统中容量的提高,对系统原有的区间或局部振荡模式改变不大,振荡特性有所变化.
2)双馈机组由于发电机内部转子电阻较小,阻尼转矩抑制振荡能力有限,会导致增加一个风机所在区域的局部振荡模式,其穿透功率的增加会减弱此局部振荡模式的阻尼.
3)直驱机组的发电机由于通过电力电子变流器与电力系统完全解耦,换流器控制转速和电气功率,随着穿透功率的增加能提高区域内发生的与风电机组相关的局部振荡的阻尼.
4)双馈机组系统都增加了与风电场强相关的振荡模式,但这些振荡模式具有较好的阻尼特性.
5 结 语
本文分析了两种风电机组的数学模型,通过强耦合两区域系统的算例,得出风机并网后,增加了系统的强相关的振荡模式,且有很好的阻尼特性,而对系统阻尼特性的改变不明显.当风电机组在系统中的容量提高时,对系统原有的同步机组区间或局部振荡模式改变不大,而振荡特性有所变化.双馈机组穿透功率的增加会减弱新增局部振荡模式的阻尼,直驱机组穿透功率增加能提高区域内发生的与风电机组相关的局部振荡的阻尼.
[1]王忱,石立宝,姚良忠,等.大规模双馈型风电场的小干扰稳定分析[J].中国电机工程学报,2010,30(4):63-70.WANG Chen,SHI Li-bao,YAO Liang-zhong,et al.Small signal stability analysis of the large-scale wind farm with DFIGs[J].Proceedings of the CSEE,2010,30(4):63-70.(In Chinese)
[2]张宝群,张伯明,吴文传.基于小干扰稳定的双馈感应电机电磁模型降阶分析[J].电力系统自动化,2010,34(10):51-55.ZHANG Bao-qun,ZHANG Bo-ming,WU Wen-chuan.Small signal based reduced electromagnetic model analysis of double fed induction generator[J].Automation of Electric Power Systems,2010,34(10):51-55.(In Chinese)
[3]杨涛,郑涛,迟永宁,等.大规模风电外送对电力系统小干扰稳定性影响[J].中国电力,2010,43(6):20-25.YANG Tao,ZHENG Tao,CHI Yong-ning,et al.Impact of large scale wind power transmission of system small signal stability[J].Electric Power,2010,43(6):20-25.(In Chinese)
[4]GAUTAM D,VITTAL V,HARBOUR T.Impact of increased penetration of DFIG-based wind turbine generators on transient and small signal stability of power systems[J].IEEE Transactions on Power Systems,2009,24(3):1426-1434.
[5]马幼捷,张继东,周雪松,等.基于分岔理论的含风电场电力系统静态电压稳定问题研究[J].电网技术,2008,32(9):74-79.MA You-jie,ZHANG Ji-dong ,ZHOU Xue-song,et al.Study on steady state voltage stability of power system containing wind farm based on bifurcation theory[J].Power System Technology,2008,32(9):74-79.(In Chinese)
[6]洪芦诚,石立宝,姚良忠,等.计及风电场发电功率不确定性的电力系统模糊潮流[J].电工技术学报,2010,25(8):116-130.HONG Lu-cheng,SHI Li-bao,YAO Liang-zhong,et al.Fuzzy modeling and solution of load flow incorporating uncertainties of wind farm generation[J].Transactions of China E-lectro technical Society,2010,25 (8):116-130.(In Chi-nese)
[7]陈功贵,李智欢,陈金富,等.含风电场电力系统动态优化潮流的混合蛙跳算法[J].电力系统自动化,2009,33(4):25-30.CHEN Gong-gui,LI Zhi-huan,CHEN Jin-fu,et al.SFL algorithm based dynamic optimal power flow in wind power integrated system [J].Automation of Electric Power Systems,2009,33(4):25-30.(In Chinese)
[8]LI H,CHEN Z.Overview of different wind generator systems and their comparisons[J].IET Renewable Power Generation,2008,2(2):123-138.
[9]李建林,许洪华.风力发电系统低电压运行技术[M].北京:机械工业出版社,2008.LI Jian-lin,XU Hong-hua.Wind power system low voltage ride through technology[M].Beijing:China Machine Press,2008.(InChinese)
[10]张红光,张粒子,陈树勇,等.大容量风电场接入电网的暂态稳定特性和调度对策研究[J].中国电机工程学报,2007,27(31):45-51.ZHANG Hong-Guang,ZHANG Li-zi,CHEN Shu-yong,et al.Studies on the transient behavior and dispatching strategy of power system integrated with large scale wind farms[J].Proceeding of CSEE,2007,27(31):45-51.(In Chinese)
[11]HE Li,CHEN Z.Overview of different wind generator systems and their comparisons[J].IET Renewable Power Generation,2008,2(2):123-138.
[12]石立宝,戴世强,徐政,等.大规模双馈型风电场并网的系统暂态稳定仿真[J].电力系统及其自动化学报,2009,21(4):1-7.SHI Li-bao,DAI Shi-qiang,XU Zheng,et al.Comparison of effect of different wind turbines on power grid transient stability[J].Proceedings of the CSU-EPSA,2009,21(4):1-7.(In Chinese)
[13]申洪,梁军,戴慧珠.基于电力系统暂态稳定分析的风电场穿透功率极限计算[J].电网技术,2002,26(8):8-11.SHEN Hong,LIANG Jun,DAI Hui-zhu.Calculation of wind farm penetration based on power system transient stability analysis[J].Power System Technology,2002,26(8):8-11.(In Chinese)
[14]SLOOTWG J G,De HAAN S W H,POLINDER H,et al.General model for representing variable speed wind turbines in power system dynamics simulations[J].IEEE Transactions on Power Systems,2003,18(1):144-151.

