基于多目标遗传算法的起重机吊装路径规划＊

邓乾旺，高礼坤，罗正平，李 枭

（湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙 410082）

虚拟场景中起重机无碰撞吊装路径规划属于环境信息已知的全局路径规划问题.全局路径规划方法根据已获知的环境信息，对环境进行建模，为起重机规划出一条满足约束条件和目标的吊装路径.目前，国内外的研究机构、学者对吊装路径规划做出了大量的研究成果，比如Morad［1］等人基于人工智能的方法开发出一款Path－Finder系统，该系统在Walk－thru环境中运用主动干涉检测盒启发式搜索方法来确定真实作业空间中的最优吊装路径.Reddy［2］等人采用了C－空间的原理和启发式搜索算法对起重机的无碰撞吊装路径规划过程进行研究.

起重机空间无碰撞吊装路径规划本质上是一个多性能指标的NP完全问题，这其中需要满足多个优化参数，例如最短距离、最小时间和最低耗能等，很难为其求解单一的优化解.传统路径规划方法有可视图法、栅格法和A＊等启发式算法［3－5］.在解决空间多自由度的路径规划问题时，上述算法的搜索速度、精度和解空间不足.近年来，遗传算法在复杂多目标优化问题中的应用已成为研究的热点，然而，多数文献仅对平面路径规划问题进行优化［6－7］，针对空间多自由度路径规划这一类多关节多约束多目标优化问题的研究较少.Kazuo Sugihara and John Smith［8］用遗传算法进行路径规划的研究具有一定的可行性和有效性，然而该文提出的路径空间栅格划分法不能解决规划速度与规划精度之间的矛盾：栅格密度小，则搜索精度差；若密度大，则数据计算量大，计算速度低.因此进化较多的搜索过程需要占据较大计算时间和存储空间.

本文将遗传算法应用于起重机多目标路径优化问题，通过分析作业场景模型和起重机位姿空间模型，将路径空间分割成多个路径平面，然后对路径平面进行栅格化处理，建立平面路径规划模型，最后应用遗传算法原理建立吊装物的路径点信息模型来确定起重机的多个吊装路径.该算法通过为场景模型添加包围盒属性来保证路径空间的搜索精度和路径的可行性，并添加新的记忆算子来提高计算效率和收敛速度，对于运用遗传算法求解空间多自由度的路径规划问题有一定的指导意义.

1 路径规划模型的建立

1.1 作业场景模型

全地面起重机臂架组合形式有主臂、主臂＋辅助臂（副臂、塔臂或动臂）两种，吊装运动有回转、变幅和卷扬3种方式［9］.根据起重机的吊装运动特点，将吊装场景划分成两个路径空间，为便于表述将其投影至XOY平面上（如图1所示）.定义r，R分别为起重机最小和最大的工作半径，吊装幅度Fd∈［r，R］，S和T分别为吊装物的起吊点和目标点，O为起重机回转中心，OS和OT分别为起始边和终止边，其中，Q1为自起始边沿逆时针（左转）方向指向终止边的扇形区域，角度范围为W1；Q2为自起始边沿顺时针方向（右转）指向终止边的扇形区域，角度范围为W2.

图1 路径空间的划分Fig.1 The division of path space

将三维场景划分为障碍物静态空间与起重机动态空间两部分.计算在工作区域内的M个障碍物的检测区域，其幅长范围fi∈［li，Li］和角度范围γi∈［vi，Vi］，然后自初始位置沿逆时针方向进行排序，依次将检测区域记为qi（i＝1，2，…，M），若qi在OX正向轴上，则将该障碍物划分至第一和第四象限两部分.图1中障碍物B1的检测区域q1的幅长范围f1∈［Ob1，Ob2］，角度范围γ1∈［θ1，θ2］；障碍物 B3的检测区域被分成两部分，γ3∈ ［0，∠b0Ob5］∪γ3∈［∠b0Ob'5，2π）.

起重机当前回转平面的回转角为ω，将起重机的动态空间划分成主臂、辅助臂和吊装物三个空间，偏移角为θ（设wd，ld为吊装物的长和宽），令吊装物空间的最大回转半径，主臂空间的最大回转半径fL，辅助臂空间的最大回转半径fF.

1.2 起重机位姿空间模型

起重机吊装过程实际上就是起重机通过调整运动形式将吊装物从起吊点安全移到目标点的过程.在真实吊装时，一般不允许臂架跨过车头所在的区域Q0，若Q0∈Qk（k＝1或2），则将Qk空间定义为禁吊空间.图2所示为路径空间Qk（k＝1）内某一吊装路径中吊装物底面中心点运动轨迹，“G1→G2”表示上幅过程，“G2→G3”表示卷扬起升过程，“G3→G4”表示回转过程，“G4→G5”表示下幅过程.将吊装物底面中心点运动轨迹中起重机运动形式变化时的拐点视为路径点，Gi（i＝1，2，…，n，n为路径点个数）表示吊装路径中第i个路径点，将路径点所在平面Πj（j＝1，2，…，m，m为路径平面个数）定义为吊装路径中第j个路径平面.设路径平面Πj和Πj＋1的回转角（OXj轴与OX轴沿回转方向的角度值）分别为wj、wj＋1.其中，每个路径平面上至少有两个不重合的路径点，wj＜wj＋1；G1和Gn分别表示起始点S和目标点T，且各自分布在Π1和Πm路径平面上；平面Πj上的最后一个路径点（尾路径点）Gi与平面Πj＋1上的首路径点Gi＋1的坐标相同.

图2 路径点运动轨迹Fig.2 The movement trajectory of path points

结合起重机运动的位姿空间，将路径平面Πj进行栅格化处理.取沿Xj轴方向的栅格间隔△a，沿Z轴方向的栅格间隔△b.根据起重机运动形式的大小与方向如图3所示，△f，△w和△zh分别表示变幅、回转和卷扬时路径点的步长.为方便对路径点进行编码，令 △zh＝N0×△zf（或△zf＝N0×△zh，N0取正整数），取△a＝△xf，△b＝△zf（或△b＝△zh）.

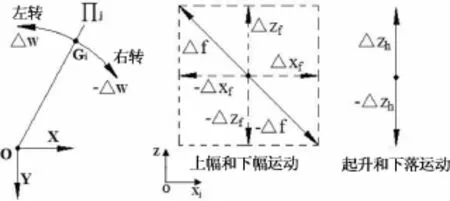
图3 路径点运动方向及步长Fig.3 The movement direction of path points and step size

将起重机动态空间投影至路径平面上，且栅格线的交点视为路径点.若起重机动态空间满足fd∈fi∩ （ω∈γi∪≤θ），则将障碍物qi的检测区域也投影至该平面上，如图4所示.当起重机、吊装物和作业环境（障碍物和地面等）三者之间出现重叠时，则更新重叠部分的包围盒子节点进行碰撞检测计算.若Gi在该位置发生碰撞，则将该路径点视为不可行路径点.

图4 起重机位姿空间栅格化Fig.4 The grids of pose space of crane

1.3 多目标问题表述

在起重机三维空间的吊装路径中，需要满足工作区域约束条件G1（P），使吊装物在可行的区域内进行吊装；还要满足无碰撞约束条件G2（P），使吊装路径安全无碰撞.为了使吊装路径的路程最短，需要对路程度量函数F1（P）进行优化；路径中每一次的动作改变，必然带来机构的启制动，从而造成对起重机的载荷冲击.为减小这种冲击，需要对路径点度量函数F2（P）进行优化［10］.从安全角度来看，当路径段“Gi→Gi＋1”跨过或靠近某障碍物时，当起重机或吊装物进入该障碍物的检测区域时，取在该位置时的中间点Ji.Ji沿图3中六个方向运动时，可能存在六个发生碰撞的路径点gt（t＝1，…，6），为减少碰撞的情况，需要对危险性度量函数F3（P）进行优化.

参数设定：

m和n分别代表路径平面和路径点个数；

Gi代表路径点；

P 代表吊装路径，P＝ ｛G1，G2，…，Gn｝；

CA起重机包围盒空间；

CB吊装物包围盒空间；

CC作业场景包围盒空间.

目标函数定义：

1）路程度量函数

式中：d（Gi，Gi＋1）为路径点Gi和Gi＋1的距离，

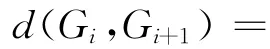
2）路径点度量函数

3）危险性度量函数

约束条件：

1）工作区域约束条件G1（P）：

xi≥r∪xi≤R，xi是路径点Gi在Xj轴上的坐标值；

2）无碰撞约束条件G2（P）：

（CA∩CB）∪ （CA∩CC）∪ （CB∩CC）＝Φ.

2 基于多目标遗传算法的路径规划

面向起重机空间路径规划的多目标遗传算法是通过遗传算子产生子代，再根据约束条件和适应度函数选择有优势的子代进行繁殖，最终达到逐步逼近最优解的目的.多目标路径规划问题描述为：

2.1 优势个体选择策略

优势个体选择策略分为约束占优和目标值占优两部分内容.

1）设路径P1和P2的目标值向量F（P1），F（P2）分 别 是 ｛F1（P1），…，FN（P1）｝和 ｛F1（P2），…，FN（P2）｝，若满足条件：∀i∈ （1，2，…，N），有Fi（P1）≤Fi（P2），且 ∃i（1，2，…，N），使 Fi（P1）＜Fi（P2），称路径P1对路径P2目标值占优.

2）将满足约束条件G（P）的路径设为可行性路径，否则，为不可行路径.以下两个条件有一个成立时，称路径P1对路径P2约束占优：a）路径P1为可行性路径，路径P2为不可行性路径；b）路径P1，P2同时为可行性路径或不可行性路径时，路径P1对路径P2目标值占优［11］.

2.2 编码、译码过程

2.2.1 编 码

采用链表方式表示每一染色体，每个染色体代表一条路径，链表中每一个元素表示路径中的一个节点，对节点采用路径点编码方式建立路径点模型，如图5所示，ωj表示路径平面∏j的回转角，（xi，yi）表示路径点Gi在其所在路径平面的局部坐标.

图5 路径点编码Fig.5 The coding of path points

2.2.2 译 码

译码就是将一组连续的路径点编码信息转化成起重机具体的运动形式的过程.定义记录吊装路径的矩阵p［u］［v］（u＝1，2，…，n－1），表示起重机的第u个动作在运动形式v（v＝0，1，2，3）时的运动量w，其中，v＝1时表示回转，当w＞0表示左转，否则表示右转；v＝2时表示变幅，当w＞0表示上幅，否则表示下幅；v＝3时表示卷扬，当w＞0表示上升，否则表示下落.初始化p［u］［v］＝0，译码步骤如下：

步骤1：读取路径点Gu（u＝1），其坐标和所在路径平面∏j的回转角分别为（xu，zu），wj.

步骤2：读取路径点Gu＋1，若Gu，Gu＋1不在同一个路径平面∏j内，则令p［u］［1］＝（wj＋1－wj）.若Gu，Gu＋1都在∏j内，当xu＋1≠xu时，表示变幅运动，则令P［u］［2］＝△α×（xu－xu＋1）／△a；当xu＋1＝xu时，表示卷扬运动，则令P［u］［3］＝（zu＋1－zu）.令u＝u＋1，执行下一步.

步骤3：判断u是否等于n（即Gu是否为目标点），若是，则完成该路径的译码过程；否则，转到步骤2.

2.3 种群初始化

根据路径的编码方式，将种群初始化过程分为两个部分.一部分是路径平面的均匀分割，∏j至∏j＋1是由连续的回转运动联系起来的，如图6所示.将路径空间分割成m个间距为Δw的路径平面；路径平面上的路径点采用启发式算法随机产生，首先随机产生平面∏j上的首尾路径点Gi和Gi＋1和平面∏j＋1上的尾路径点，然后在两路径点之间运用2.4节的插入算子插入中间点.

图6 种群初始化Fig.6 Population initialization

2.4 遗传算子

本算法涉及六个遗传算子：记忆算子、选择算子、插入算子、交叉算子、变异算子和删除算子.

1）记忆算子

为减小算法中的碰撞检测的时间耗损，需对检测过程进行简化.若在∏j平面上某路径点Gi处，吊装物或起重机与作业场景发生碰撞，即（CA∩CC）∪（CB∩CC）≠Φ，则记忆该路径点为平面∏j的不可行节点，在该平面上进行插入和变异操作时要避开平面不可行节点.若吊装物与臂架发生碰撞，即CA∩CB≠Φ，若路径点Gt（t＝2，…，n－1）满足xt≤xi∩zt≥zi，则记忆该路径点为路径空间的不可行节点，在该路径空间内进行插入和变异操作时要避开空间不可行节点.

2）选择算子

采用两种不同的选择算子，第1种算子的功能是选择优良的个体参与繁殖；第2种算子的功能是选择较差或发生碰撞的子路径进行变异.

3）插入算子

对于同一路径平面上的某两个相邻可行性路径点Gi，Gi＋1，若沿±△f，±△zh四个方向Gi与Gi＋1之间无法形成路径或Gi与Gi＋1之间形成的路径与障碍物发生碰撞时，可能需要插入nt（nt≥0）个可行性路径点.若插入的路径点或新路径点产生的新路径不可行，则重新选取插入量（改变倍率值κ1，κ2）和插入方向再进行计算判断.则插入原则满足：

其中，K1∈N∪K2∈N，κ1表示沿变幅方向插入的新路径点相对于Gi的步进倍率，且κ2＝0上幅时f＝－1，κ1＜0，下幅时f＝1，κ1＞0；κ2表示沿卷扬方向插入的新路径点相对于Gi步进的倍率，且κ1＝0，起升时κ2＞0，下落时κ2＜0.

4）交叉算子

等概率地从两父代个体中随机选择两个路径点（起点和终点除外）或两个路径平面，交换两个体在交叉处的部分染色体.

5）变异算子

规定路径点沿图中上幅、下幅、卷扬和下落四个方向进行变异.

a）当路径可行时，随机选择路径中的几个路径平面，任意一组相邻路径平面的路径点之间形成一条子路径段，计算这些子路径段的每一个目标值和约束值，选择较差的子路段所对应的路径点进行变异；如果所有的子路段都互不占优，则随机选择一段进行变异，并保证变异后的路径仍为可行性路径.

b）当路径点不可行时，对该路径点坐标依概率进行较大范围调整.根据图中吊装物与障碍物的相对位置，使其变异到障碍物余量范围ε之外；否则，在两端点中随机选择一点进行变异.若变异后的路径点为可行性路径点，变异后产生的新路径为可行性路径，则用偏移后的新节点替换变异节点；否则重新选取变异量（改变倍率值κ3和κ4）和变异方向再进行计算判断.变异公式如下：

xi＝xi＋f×κ3×Δxf，

zi＝zi＋f×κ3×Δzf＋κ4×Δzh.

其中，κ3，κ4分别表示沿变幅和卷扬方向的变异倍率，取值规律同κ1和κ2一致.

6）删除算子

删除算子主要分4种：图7（a）中A和C，C和E都直接可达，则删除B和D 路径点；图7（a）中路径点C在路径中出现了两次，则需删除位于相同路径点间的所有点；图7（b）中节点B和C是直接可达的，则删除位于B和C之间的所有路径点；若∏j－1上的尾路径点和∏j＋1上的首路径点是直接可达的，则删除路径平面∏j及其路径点.

图7 删除算子Fig.7 Delete operator

3 实例验证

在全地面起重机大型工程吊装方案规划系统上运用OSG与VC＋＋9.0实现了该算法.以图8火电吊装场景为例，作业场景为100m×100m的平面，选取“主臂＋副臂”工况的全地面起重机，主臂长为48.4m，副臂长为16.0m，主辅臂夹角为15°，吊装幅度fd∈［16，52］（m）；Q1为可吊装区域.图8为起重机在起吊点时的姿态，黄色区域为目标点位置；初始化路径平面间夹角Δw＝5°；令△α＝1°，起重机每变幅1°使吊装物上升0.80m，设置路径点步长△f＝1.12m，△xf＝0.78m，△zf＝0.80m，△zh＝0.80m，则栅格间距△a＝0.78m，△b＝0.80m.

图8 吊装作业场景Fig.8 The lifting operation scene

本文算法的运行参数为：群体规模为50，最大进化代数T＝80.前T／2代中，交叉概率Pc＝0.5，变异概率Pm＝0.5，删除概率Pd＝0.8；后T／2代中，Pc＝0.2，Pm＝0.1，Pd＝0.4.算法结束后，收集所有结果中与三个目标函数相对应的较优路径作为Pareto解集的一个逼近解集，相关较优路径矩阵对应目标函数值解集分布如图9所示.针对三个目标函数挑出三条路径依次为：

图9 Pareto解集对应目标函数值分布Fig.9 Distribution of objective function value of Pareto solution set

1）路径最短：上幅16°→起升8m→上幅14°→左转116.57°→下幅39°；其吊装路径矩阵为：

2）拐点最少：起升8m→上幅28°→左转116.57°→ 下幅37°；其吊装路径矩阵为：

3）危险最小：起升16m→上幅26°→左转30°→起升6.4m→左转86.57°→下幅32°→下落15.2 m；吊装路径矩阵为：

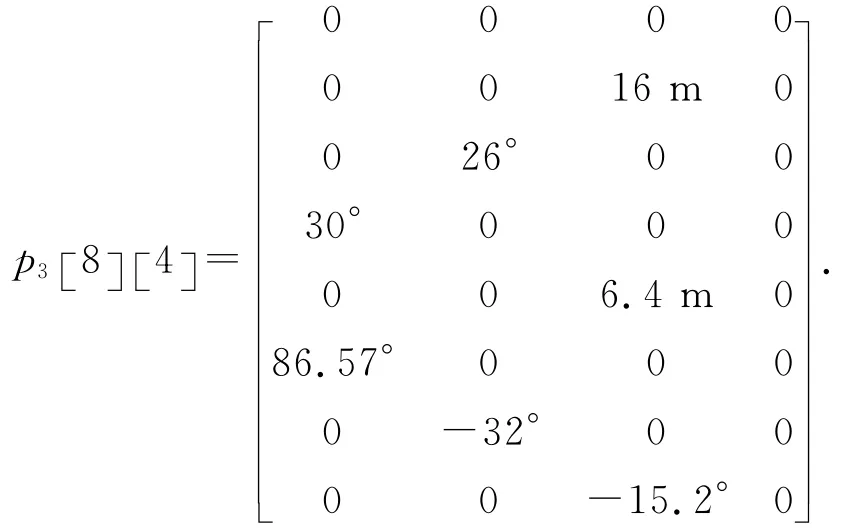
各路径的度量函数值如表1所示.

表1 各路径的目标函数值Tab.1 Object function value of paths

本文还将其与经典遗传算法（即没有记忆算子与删除算子）进行了比较.相关目标函数收敛对比如图10所示.其中改进遗传算法与经典遗传算法均能获得较好的Pareto解集，但是改进遗传算法有利于提高收敛速率，减少计算时间.

图10 度量值的收敛对比Fig.10 Comparison of convergence of measurement value

4 结 论

针对起重机空间多自由度的吊装路径规划问题，提出了一种基于多目标遗传算法的路径规划方法.该算法根据起重机吊装运动特点，设计了三维空间的路径点编码机制和适合于路径规划的具有启发作用的遗传算子，且综合考虑了起重机吊装路径的多个目标，能够同时提供不同特点的多条路径.最后通过实例验证，表明了该算法的有效性.

［1］MORAD A A，CLEVELAND A B，BELIVEAU Y J，et al.Path－finder：Al－based path planning system［J］.Journal of Computing in Civil Engineering，1992，6（2）：114－128.

［2］REDDY H R，VARGHESE K.Automated path planning for mobile crane lifts［J］.Computer－Aided Civil and Infrastructure Engineering，2002，17（6）：439－448.

［3］杨淮清，肖兴贵，姚栋.一种基于可视图法的机器人全局路径规划算法［J］.沈阳工业大学学报，2009，31（2）：226－229.YANG Huai－qing，XIAO Xing－gui，YAO Dong.A V－graph based global path planning algorithm for mobile robot［J］.Journal of Shenyang University of Technology，2009，31（2）：226－229.（In Chinese）

［4］朱磊，樊继壮，赵杰，等.基于栅格法的矿难搜索机器人全局路径规划与局部避障［J］.中南大学学报：自然科学版，2011，42（11）：3421－3428.ZHU Lei，FAN Ji－zhuang，ZHAO Jie，et al.Global path planning and local obstacle avoidance of searching robot in mine disasters based on grid method［J］.Journal of Central South University：Science and Technology，2011，42（11）：3421－3428.（In Chinese）

［5］贾庆轩，陈刚，孙汉旭，等.基于A＊算法的空间机械臂避障路径规划 ［J］.机械工程学报，2010，46（13）：109－115.JIA Qing－xuan，CHEN Gang，SUN Han－xu，et al.Path planning for space manipulator to avoid obstacle based on A＊algorithm［J］.Chinese Journal of Mechanical Engineering，2010，46（13）：109－115.（In Chinese）

［6］刘旭红，张国英，刘玉树，等.基于多目标遗传算法的路径规划［J］.北京理工大学学报，2005，25（7）：613－616.LIU Xu－hong，ZHANG Guo－ying，LIU Yu－shu，et al.Path planning based on multi－objective genetic algorithm［J］.Journal of Beijing Institute of Technology，2005，25（7）：613－616.（In Chinese）

［7］申晓宁，郭毓，陈庆伟，等.多目标遗传算法在机器人路径规划中的应用［J］.南京理工大学学报，2006，30（6）：659－663.SHEN Xiao－ning，GUO Yu，CHEN Qing－wei，et al.Application of multi－objective optimization genetic algorithm to robot path planning［J］.Journal of Nanjing University of Science and Technology，2006，30（6）：659－663.（In Chinese）

［8］KAZUO SUGIBARA，JOHN SMITH.Genetic algorithms for adaptive motion planning of an autonomous mobile robot［C］／／Computational Intelligence in Robotics and Automation：1997 IEEE International Symposium，Monterey，USA，1997.

［9］杜海岩.工程机械概论［M］.成都：西南交通大学出版社，2004.DU Hai－yan.Introduction to mechanical engineering［M］.Chengdu：Southwest Jiaotong University Press，2004.（In Chinese）

［10］张玉院.移动式起重机无碰撞路径规划的设计与实现［D］.大连：大连理工大学，2010.ZHANG Yu－yuan.Design and implementation of collision－free path planning for mobile crane［D］.Dalian：Dalian University of Technology，2010.（In Chinese）

［11］关志华.面向多目标优化问题的遗传算法的理论及应用研究［D］.天津：天津大学，2002.GUAN Zhi－hua.Research on the theory and application of genetic algorithm for multi－objective optimization problems［D］.Tianjing：Tianjing University，2002.（In Chinese）