基于意图辨识的线控汽车紧急转向控制方法*
何 磊,马伯祥,宗长富,郑宏宇
(1.吉林大学 汽车仿真与控制国家重点实验室,吉林 长春 130025;2.中国第一汽车股份有限公司 技术中心,吉林 长春 130011)
线控转向系统由于取消了转向盘与转向器的机械连接并通过电子控制单元控制转向,使得转向传动比的设计自由度变大,能够实现保证汽车稳态增益不变的理想转向传动比,让汽车驾驶适合于更多的人群,特别是让更多的非职业驾驶员容易掌握汽车动力学特性[1].但是,驾驶员在紧急转向时,按照理想转向传动比得到的横摆角速度动态响应无论在响应速度、超调量,还是稳定时间上都不是理想的,通过加入横摆角速度反馈控制则可以降低超调量、缩短稳定时间.横摆角速度反馈控制仅在紧急转向工况下进行叠加,因此,需引入驾驶员转向意图辨识环节,以此判定何时进行横摆角速度反馈控制.
驾驶员转向意图辨识本质上是一个模式识别过程,在此领域主要使用的模式识别方法有模糊模式识别、神经网络模式识别和统计模式识别等.其中,神经网络模式识别方法中神经网络的设计和实现没有理论依据可以借鉴,只能依赖于经验[2].结构模式识别方法适合结构性强的模式识别,其抗噪声能力差,计算复杂度高[3].统计模式识别有很多具体的方法,进入21世纪以来,Bayes决策理论越来越多地用来解决具体的模式识别问题,并产生了优异的分类性能[4].基于Bayes决策理论的隐式马尔可夫模型(Hidden Markov Model,简称 HMM),由于具有处理时间序列数据的特性,近年来广泛应用于语音识别和驾驶员行为辨识领域中.以HMM为基础的模式识别方法随着样本的增加,模型会变得越来越好.
鉴于转向驾驶行为的强时间序列性,本文以HMM为基础理论,搭建多维高斯HMM模型,对模型中的参数进行训练,辨识驾驶员的转向意图,并根据辨识出的转向意图,对车辆进行不同模式的控制:在正常转向时,车辆按照理想转向传动比控制;在紧急转向时,在理想转向传动比控制基础上叠加横摆角速度反馈控制.
1 驾驶员转向意图辨识方法
1.1 隐式马尔科夫模型
隐式马尔科夫包含双重的随机过程,分别是Markov链和一般的随机过程.在HMM里,状态是不能直接看到的,观察者只能看到基于状态产生的模型输出(观察序列).每一个状态与其可能的观察值之间的关系通过一般的随机过程描述;状态间的转移通过Markov链来描述.应用这两个随机过程,能透过HMM产生的观察序列,得到状态时间序列和模型的相关信息.
一个HMM模型一般描述成λ=[N,M,π,A,B],其中π为各个状态在第一时刻出现的概率;A为状态转移概率矩阵,代表各个状态间转移的概率;B为在某个状态下,出现某观察值的概率;N为模型的状态数;M为每个状态下不同观察值的数目.为了简洁,把模型描述成λ=[π,A,B].用HMM来处理实际问题时,需要解决以下三个基本问题.
问题1 给定观察序列O=(O1,O2,…,OT)和模型λ,计算模型产生观察序列的可能性,即计算P(O|λ).这可以用来解决评价问题,也可以用来检验一个模型与观察序列的匹配程度.问题1的解决方法通常是采用 Forward-Backward算法[5].
问题2 给定观察序列O=(O1,O2,…,OT)和模型λ,确定一个最佳的状态序列Q={Q1,Q2,…,QT},来最好地解释给定的观察序列.问题2可以用来挖掘模型的隐含成分,找出最优的状态序列,其解会有很多形式,主要在于最优状态序列的定义(即最优标准的选择).最广泛使用的优化准则是从整个状态序列上考虑:找到最优的状态序列,使得P(Q|O,λ)最大.在实际中并没有一个“最佳”的定义,基于动态编程方法的Viterbi算法[6]得到的结果通常是满意的,但并不能保证它是绝对意义的“最优”.
问题3 调节模型参数使P(O|λ)最大.问题1和问题2求解的前提都是给定模型参数λ,因此,确定模型参数是一个以HMM理论为基础的问题需首要解决的任务(即模型的训练过程).在给定模型初始参数后,利用某种算法对模型参数进行迭代,使得观察序列(训练数据)在最终的模型参数下,产生的概率最大.HMM模型参数训练应用的算法为Baum-Welch算法[7],它是多次迭代优化的算法.模型训练过程可以描述为:将选取的模型初始参数λ=[π,A,B]和观察序列O=(O1,O2,…,OT)代入重估公式,求得一组新的参数,使得>P(O|λ).经过重估公式计算得到的与原始的相比,能更好地表示观察序列.不断重复迭代这个过程直到模型参数λ变化不再明显.
1.2 多维高斯HMM建模及模型参数的训练方法
鉴于HMM的处理时序序列的能力和强的统计学基础,本文借助吉林大学的驾驶模拟器采集转向盘转角和转向盘角速度的数据,对数据预处理后,用Baum-Welch算法对紧急转向、正常转向和直线行驶三个转向驾驶行为HMM模型的参数进行优化.然后借助于NI公司的LabVIEW和驾驶模拟器对转向驾驶行为进行实时的验证.整个过程如图1所示.

图1 驾驶员转向意图辨识过程Fig.1 The process of driver steering intention recognition
模型采集的数据都是连续的,为了防止信号量子化造成的信号失真,本文应用多维高斯HMM理论来搭建驾驶员转向行为模型:直线行驶、正常转向及紧急转向.这些驾驶员转向行为对应的多维高斯HMM模型的模型结构如图2所示.
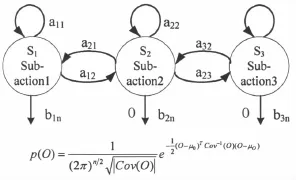
图2 多维高斯HMM模型Fig.2 Multidimensional Gauss HMM model
模型中隐形的状态对应着该模型表征的驾驶员转向行为的子行为(该驾驶员驾驶行为的不同程度分级).多维高斯HMM的模型参数可以表示为λ=[π,A,C,μ,δ].其中,π为初始状态概率矢量;A为状态转移概率矩阵;C为混合高斯函数权系数矩阵;μ为混合高斯函数均值矩阵;δ为混合高斯函数均方差矩阵.
解决以HMM为基础的问题的首要任务就是确定模型参数.对上文提到的3个驾驶员转向行为的多维高斯HMM来说,其观察序列可以用向量的形式描述,如式(1):

其中,a(t)为转向盘转角;b(t)为转向盘角速度.多维高斯HMM的观察概率密度用式(2)来表述:

其中,cjm为对应于状态j的第m个混合分量的混合系数,N[μjm,Ujm]代表一个高斯分布函数,μjm和Ujm分别是高斯分布函数的平均值和协方差.本文中,μjm和Ujm分别代表某转向行为下的转向盘转角和转向盘角速度二维信号的均值和协方差矩阵.
cjm,μjm,Ujm的参数重估公式如式(3)~(5)所示:

训练数据的采集借助于驾驶模拟器,选定正常转向、紧急转向和直线行驶三个工况,其中正常转向和直线行驶是在驾驶模拟器的一般道路试验场景里完成的,紧急转向是借助于双移线场景完成的.不同年龄的专业驾驶员对应每个工况的多次试验数据构成了整个训练数据集.
对数据集的数据进行滤波处理,将滤波后的数据按辨识长度进行截断、剔除异常数据段之后,借助于K-means算法确定驾驶员意识上的直线行驶、正常转向和紧急转向的界限值,根据这个界限值对截断后的数据段进行分类,以得到驾驶员直线行驶、正常转向及紧急转向驾驶行为模型的训练数据.编写MATLAB程序,结合 HMM 工具箱里的Baum-Welch算法,训练得出多维高斯HMM模型参数.
2 线控汽车紧急转向控制方法
车辆紧急转向时,转向盘输入的速度较大,车辆瞬态转向特性表现较为明显.为了弥补车辆设计时的瞬态转向响应品质的不足,在车辆理想转向传动比控制的基础上,加入横摆角速度反馈叠加转角控制.系统的控制结构如图3所示,转向执行器的目标控制转角δd由δ1和δ2两部分组成.其中,δ1是根据理想转向传动比计算得出的,理想传动比1/G由转向盘转角δsw和纵向车速Vx确定[8].δ2是横摆角速度反馈控制叠加转角.当辨识驾驶员为正常转向时,横摆角速度叠加转角为0;当辨识驾驶员为紧急转向时,横摆角速度叠加转角由期望横摆角速度和实际横摆角速度的偏差经过PID调节得到.

图3 紧急转向控制方法Fig.3 Emergency steering control method
从控制结构上看,理想传动比是内环控制,它能有效地进行车辆稳定性转向控制;横摆角速度反馈是外环控制,只在特定工况下进行.采用理想传动比控制,可以保证汽车的转向控制算法在全工况内都切实有效.由于实际转向工况复杂,不全是稳态转向,而驾驶员在紧急转向时接近阶跃转向,此时按照理想传动比计算的转向输入横摆角速度动态响应无论从响应速度、超调量,还是稳定时间上都不是理想的,若通过叠加横摆角速度反馈控制,则可提高车辆的瞬态转向品质.
2.1 理想转向传动比设计
线控转向系统转向传动比控制策略设计结合了理想转向传动比和模糊控制转向传动比各自的优点[9].当汽车低速和高速行驶时采用模糊控制转向传动比,满足驾驶员低速转向灵敏性和高速转向平稳性的要求.汽车中速行驶时,采用理想转向传动比,保证汽车横摆角速度增益不变,降低驾驶难度和负担,使驾驶员更容易掌握汽车动力学特性.因此,线控转向系统转向传动比具体设计如下:1)当车速0~20km/h时,转向传动比保持为固定值6;2)车速在20~30km/h时,转向传动比从6平稳过渡到理想转向传动比;3)考虑基于模糊控制的车速在90km/h时,模糊控制转向传动比与理想转向传动比较接近,均为18左右.因此,选择车速在30~90km/h时,采用理想转向传动比;车速为90~95km/h时采用数据拟合的方法实现传动比向模糊控制转向传动比平滑过渡;车速大于95 km/h时,采用模糊控制转向传动比.具体的转向变传动比如图4所示.

图4 SBW系统转向变传动比Fig.4 Variable steering ratio of SBW system
2.2 横摆角速度反馈控制的补偿转角
横摆角速度的反馈控制,首先需要得到横摆角速度的期望值rd.在汽车稳定性控制系统中,期望横摆角速度通常由线性二自由度模型得到.由于已采用理想转向传动比,因此,使用如下的横摆角速度稳态期望值:

通过转向盘转角δsw与增益Kr可以算出横摆角速度的稳态期望值rds.受最大附着力的限制,侧向加速度必须满足ay≈Vxr≤μg.因此,最终的横摆角速度期望值如式(7)所示:

控制结构中,采用一个上下限为±μg/Vx的饱和环节求得最终的理想横摆角速度rd,再经过PID控制器调节,得到横摆角速度的补偿转角.
3 实验结果分析
为验证线控转向汽车紧急转向时,叠加横摆角速度反馈控制的有效性,对比了有反馈控制和无反馈控制的实验结果.受实验设备及条件的限制,实验台实验无法给出相同的两次紧急转向输入,因此,先进行了转向盘角阶跃输入工况的软件仿真验证.仿真时,车辆以80km/h的速度行驶,施加如图5所示的转向盘转角,图6为相应的车速变化曲线.
从图7与图8的仿真结果可以看出,仅有理想传动比控制的车辆在转向盘阶跃转向1.2rad时,侧向加速度约有0.35rad/s的超调量,横摆角速度约有0.38rad/s的超调量,超调量数值均较大.在添加横摆角速度反馈控制后,侧向加速度的超调量降低了约0.32rad/s的超调量,横摆角速度的超调量降低了约0.35rad/s的超调量.不仅如此,在叠加反馈控制前,汽车瞬态转向的稳定时间约为1s,而在叠加反馈控制后,这个时间缩短为0.4s左右.由此可见,叠加反馈控制能保证车辆良好的瞬态转向特性.

图5 转向盘转角曲线Fig.5 The curve of steering wheel angle

图6 车速变化曲线Fig.6 The curve of speed

图7 侧向加速度曲线Fig.7 The curve of lateral acceleration
在进行软件仿真后,又在线控转向系统硬件在环实验台上进行了验证.实验选取了两次基本相同的工况来比较验证叠加横摆角速度反馈的必要性.图9给出了图11的驾驶员转向行为辨识结果,在角阶跃转向开始阶段准确辨识出驾驶员的紧急转向行为.其中,右侧轴线中的0表示直线行驶,1表示正常转向,2表示紧急转向.在辨识驾驶员紧急转向行为后,叠加横摆角速度反馈控制,降低阶跃转向时的横摆角速度超调量.车速变化如图10所示,两次转向盘转角输入分别如图11与图12所示.由于设计的叠加横摆角速度控制是依据驾驶员转向行为辨识结果决定的,所以在整个转向过程中,先在6~16s阶段采用转向盘转角连续正弦输入模拟正常的转向操作,再在16 s~25s采用转向盘转角阶跃输入模拟紧急转向工况.从图13与图14的实验结果可以看出,仅理想传动比的横摆角速度的超调量约为0.3rad/s,而带反馈控制的横摆角速度曲线基本消除了此超调量.汽车瞬态转向的稳定时间也缩短约0.5s.

图8 横摆角速度曲线Fig.8 The curve of yaw velocity

图9 驾驶员转向行为辨识结果曲线Fig.9 The curve of driver steering intention recognition

图10 车速变化曲线Fig.10 The curve of speed

图11 带反馈的转向盘转角曲线图Fig.11 The curve of steering wheel angle with feedback

图12 仅理想传动比的转向盘转角曲线Fig.12 The curve of steering wheel angle with ideal steering raito

图13 带反馈的横摆角速度曲线Fig.13 The curve of yaw velocity with feedback

图14 仅理想传动比的横摆角速度曲线Fig.14 The curve of yaw velocity with ideal steering raito
4 结 语
本文以HMM为基础理论,搭建多维高斯HMM模型,利用吉林大学驾驶模拟器对模型中的参数进行离线训练,达到在线辨识驾驶员转向意图的目的.根据辨识出的驾驶员转向意图,对车辆进行不同模式的控制:在正常转向时,车辆按照理想转向传动比控制;在紧急转向时,在理想转向传动比控制基础上叠加横摆角速度反馈控制.实验结果表明:驾驶员转向意图辨识结果准确,紧急转向时叠加的横摆角速度反馈控制能够有效降低线控汽车瞬态转向响应的超调量、减少稳定时间.
[1]宗长富,李刚,郑宏宇,等.线控汽车底盘控制技术研究进展及展望[J].中国公路学报,2013,2:160-176.ZONG Chang-fu,LI Gang,ZHENG Hong-yu,et al.Study progress and outlook of chassis control technology for X-bywire automobile[J].China Journal of Highway and Transport,2013,2:160-176.(In Chinese)
[2]耿冠宏,孙伟,罗培.神经网络模式识别[J].软件导刊,2008,7(10):81-83.GENG Guan-hong,SUN Wei,LUO Pei.Pattern recognition neural network[J].Software Guide,2008,7(10):81-83.(In Chinese)
[3]杨合超,宋海歌,周雪梅.模式识别的主要方法及其应用[J].电脑知识与技术,2008,S2:156-157.YANG He-chao,SONG Hai-ge,ZHOU Xue-mei.The main methods and applications of pattern recognition[J].Computer Knowledge and Technology,2008,S2:156-157.(In Chinese)
[4]卢力,田金文,柳健.统计模式识别研究进展[J].军民两用技术与产品,2003,11:39-42.LU Li,TIAN Jin-wen,LIU Jian.Advances of statistical pattern recognition[J].Aerospace Technology and Civilian Products,2003,11:39-42.(In Chinese)
[5]HE Lei,ZONG Chang-fu,WANG Chang.Driving intention recognition and behaviour prediction based on a double-layer hidden Markov model[J].Journal of Zhejiang University Science C:Computers &E-lectronics,2012,13(3):208-217.
[6]VASEGHI S V.State duration modeling in hidden Markov models[J].Signal Processing,1995,41(1):31-41.
[7]宗长富,王畅,何磊,等.基于双层隐式马尔科夫模型的驾驶意图辨识[J].汽车工程,2011,33(8):701-706.ZONG Chang-fu,WANG Chang,HE Lei,et al.Driving intention recognition based on double-layer HMM[J].Automotive Engineering,2011,33(8):701-706.(In Chinese)
[8]何磊.基于FlexRay总线的线控转向系统双电机控制方法研究[D].长春:吉林大学汽车工程学院,2011.HE Lei.Research on dual-motor control method based on FlexRay bus for steer-by-wire automobile[D].Changchun:College of Automotive and Engineering,Jilin University,2011.(In Chinese)
[9]郑宏宇.汽车线控转向路感模拟与主动转向控制策略研究[D].长春:吉林大学汽车工程学院,2009.ZHENG Hong-yu.Research on road feeling and active steering control strategy for vehicle steer-by-wire system[D].Changchun:College of Automotive and Engineering,Jilin University,2009.(In Chinese)

