7500吨浮式起重机风载荷特性分析＊

张戬杰，张 氢，秦仙蓉，廖 鑫

（同济大学 机械工程与能源学院，上海 200092）

7 500t浮式起重机是目前世界上单机回转起吊能力最大的海上浮式起重机，主要结构包括底盘、人字架、臂架及钢丝绳等，其臂架长度约110m，人字架高约51m，可广泛应用于重型桥梁安装工程、海上油气田开发的吊装作业、港口建设重大件吊装和沉船打捞等作业中.7 500t浮吊不同于常见的机械和建筑结构，其结构相对特殊、复杂.其臂架可在20°～80°范围内自由俯仰，且其臂架是由2个对称布置的桁架结构单支组成，其特点是多弦杆、腹杆等细柔杆件，启动外形复杂.此外，浮吊的工作海区广阔，可工作于近岸、浅海、深海等各种海域，作业区域地貌环境多样.因此，有必要讨论浮式起重机在不同的臂架俯仰角和风场环境下整体的基底响应.

迄今为止，对7 500t浮吊风载荷的计算大多集中于按相关规范估算和CFD数值仿真模拟［1－3］，仅限于某种特殊工况下的风载荷计算，且不能保证结果的精确.浮吊的局部刚度较好，风载荷对结构的作用主要体现在结构整体的基底响应.为此，采用高频动态天平测力技术，在同济大学TJ－2边界层风洞内分别进行了0～180°范围内不同风向角、3种不同臂架幅度、两种不同风场地貌的风洞试验，全面研究了7 500t浮吊的风载荷特性.

1 高频动态测力天平试验原理

高频动态测力天平试验原理［4－5］是基于结构的风致振动主要由一阶振型贡献这一假设，其一阶广义坐标运动方程可写成：

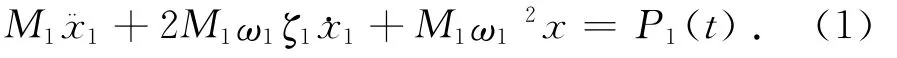
式中：M1，ω1，ζ1分别为结构的一阶广义质量、圆频率和阻尼；P1（t）为一阶广义力：

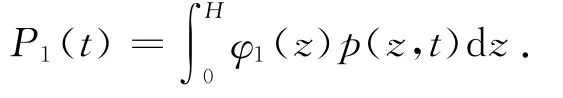
式中：H为物体的高度.当假设振型为理想振型［6］，即φ1（z）＝z／H 时，天平所测得的基底弯矩就是物体的一阶广义水平载荷.同样，如取扭矩振型为常数，则天平测得的基底扭矩就是一阶广义扭转载荷.

2 7 500 t浮吊风洞模型

以St数为相似准则［7］，并与同济大学TJ－2边界层风洞的圆盘尺寸进行匹配，最终确定7 500t浮吊高频动态天平测力风洞实验模型的缩尺因子，见表1.

表1 试验模型的缩尺因子取值Tab.1 Scale coefficients of wind tunnel test model

为方便模型制作，风洞模型不考虑座船以及回转轴承等结构，只考虑底盘、人字架、臂架、钢丝绳等主起吊结构，即将船体简化为固定基础，只对起重机本体进行风洞试验.为满足高频动态天平测力风洞实验的质量和刚度要求，确保模型在气动外形上与原型的相似性，整体结构采用ABS工程塑料，按照1∶200的缩尺比例制作风洞模型，忽略极少部分在缩尺之后尺寸过小的结构，其中钢丝绳是利用缩尺比后直径相等的钢丝绳模拟.模型底盘固结在风洞实验室的回转转盘上，如图1所示.

试验中，高频天平的固有频率约为50Hz，而试验模型的固有频率约为10Hz左右.

图1 7 500t浮吊风洞模型Fig.1 Wind tunnel test model of 7 500tfloating crane

3 试验工况

7 500t浮吊可自由航行在各海区进行作业.作业过程中，通过抛锚限制船体的运动，臂架幅度将根据作业需要发生变化，且可能在任意方向上遭遇风载荷.因此，选择以下3种参数作为试验控制参数以进行风载荷特性研究：1）风向角；2）臂架幅度；3）不同风场的地貌特征.7 500t浮吊整体是对称结构，定义来流风平行吹向浮吊中轴线时风向角为0°，按逆时针方向增加到180°，风向角间隔取为15°，每一轮试验共有13个风向，如图2所示.在0～180°风向角范围内进行测试，以模拟可能出现的各种风向角；臂架幅度采用3种典型的臂架工作位置，分别为最小幅度（俯仰角度为20°），全回转条件下的最小幅度（俯仰角度为60°），以及最大幅度（俯仰角度为80°）.7 500t浮吊所处局部风场也因不同地形而有所不同，将浮吊工作环境的风场类型概括为A类地貌（开阔海域）和B类地貌（近岸海域）.

图2 模型方位和风向角示意图Fig.2 Draft of wind inlet angle

综上所述，共需对13个风向角，3个臂架幅度，2种风场地貌特征共78种试验工况进行风洞试验.

在TJ－2边界层风洞中布置尖劈、格栅和粗糙元模拟大气边界层流场［8－9］，并完成高频天平风洞测力试验.

4 试验数据处理及结果分析

高频动态天平测力风洞试验的坐标系统，如图3所示.固定在风洞地面的坐标系o－xyz为全局坐标，风吹入方向为x轴正向，z轴正向为竖直向上，y轴按右手法则定义在水平面内，坐标原点o定义在转盘圆心的地面处；模型坐标系omodel－xmodelymodelzmodel与转盘联动，即随体坐标.初始状态时臂架反方向为xmodel轴正向，zmodel轴正向为竖直向上，ymodel轴按右手法则定义在水平面内，其坐标原点定义在转盘圆心的地面处，与固定坐标原点o重合.x轴与xmodel轴正向的夹角为风向角，记做α.基底响应值是在模型坐标系中测量得到的，结果分析在全局坐标系o－xyz中进行，因此需利用式（2）进行坐标转换.

测力试验中模型所受到的风载是非定常的气动力，由稳态时均值和脉动值两部分组成.风洞试验一般无法模拟真实的雷诺数，气动力的脉动值不够准确，因此在此仅讨论气动力稳态时的均值.按全局坐标系，Fx，Mx，Fy，My，Fz，Mz分别表示沿x 轴、y 轴及z轴的力和力矩均值.

图3 全局与模型坐标系统示意图Fig.3 Draft of global and model coordinate system

高频天平测得的基底力和力矩的平均值无量纲风力系数［10］定义如下：

式中：Ci，CMi分别为沿3个坐标轴的基底力的平均值、力矩的平均值的无量纲系数；Fi，Mi分别为沿3个坐标轴的基底力的平均值、力矩的平均值；ρ＝1.225kg／m3为空气密度；¯U为模型高度处的平均风速，A类、B类风场分别为9.5m／s，8.3m／s；H 为模型的高度，为0.35m；D为模型的特征长度，为0.77m.

4.1 风向的影响

3种臂架幅度、2类地貌对应78个风洞实验工况的数据表明：各种风向角下风载荷的基底响应大致趋势类同.这里仅以A类风场，臂架仰角为20°为例进行结果分析及讨论.臂架幅度为20°，A类风场，不同风向角下基底响应均值的无量纲系数Ci，CMi如图4所示.

图4表明，Cx，Cy，Cz，CMx，CMy，CMz6个系数均大致关于90°风向角对称或反对称，这与实际情况相符.顺风向系数Cx的数值明显高于其余5个分量系数，在风向角135°时达到最大值0.18，并不在90°风向角时达到最大值，风向角90°时Cx仅为0.157.因此，若只沿主轴方向进行结构或整机风载荷稳定性校验，则有可能漏掉实际最大风载荷.横风向系数Cy在90°风向角时为0，其余风向角时与顺风向系数Cx相互对应，在30°风向角时达到最大值－0.025.升力系数Cz保持正值，在0.025～0.05之间浮动.0°风向角时俯仰臂架直对来流，有较强的升力作用，升力系数达到最大值0.05.侧倾力矩系数CMx正负跳跃频繁，但数值较小，表明模型在风载作用下不易发生侧倾.俯仰力矩系数CMy曲线与顺风向系数Cx曲线规律相似，因顺风向风载荷是俯仰力矩的主要贡献者，且明显高于除顺风向系数Cx以外的分量系数，数值在0.07～0.1之间浮动，在风向角为135°时达到最大值为0.1.扭转力矩系数CMz在0°和180°风向角时最小，几乎为0，在90°风向角时达到最大值为0.06.这是因为风载荷作用在臂架上的扭转力矩随风向角变化产生的二次函数曲线变化.

4.2 臂架幅度的影响

图4 20°臂架俯仰角A类风场各风向角Ci，CMiFig.4 Ciand CMivs.wind inlet angle with boom luffing angle 20°and type A wind field

臂架幅度的俯仰角总共有20°，60°，80°3种工况，分别对应A和B两类风场地貌，试验数据表明A和B类风场地貌下臂架幅度对风载荷基底响应均值的影响趋势类同.这里仅以A类风场地貌为例进行结果分析及讨论.A类风场地貌，不同臂架幅度的基底力响应均值的无量纲系数Ci随风向角的变化情况如图5所示，基底力矩响应均值的无量纲系数CMi随风向角的变化曲线如图6所示.

图5 A类风场不同臂架俯仰角各风向角Ci曲线Fig.5 Civs.wind inlet angle of varies boom luffing angle

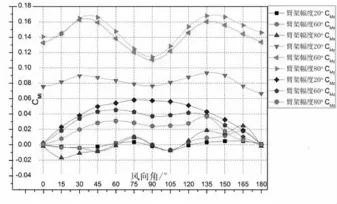
图6 A类风场不同臂架俯仰角各风向角CMi曲线Fig.6 CMivs.wind inlet angle of varies boom luffing angle

图5和图6表明，在不同臂架幅度下，Cx，Cy，Cz，CMx，CMy，CMz6个分量系数随风向角变化的曲线形状都相似，臂架俯仰角度仅影响风载荷基底响应的幅值大小，与实际情况相符.臂架幅度对顺风向系数Cx以及俯仰力矩系数CMy的影响最显著，其次是扭转力矩系数CMz，对其余系数的影响程度都不明显.

臂架俯仰角度增大，臂架的迎风面积也增加，除了90°风向角以外，顺风向系数Cx在其余各风向角下相应增大，但增幅明显减小.90°风向角时，3种臂架幅度工况下模型的迎风面积相等，因此顺风向系数Cx均为0.16.俯仰角度由20°增大为60°，风向角为45°时增幅达到最大为0.05，但由60°增大为80°时最大增幅仅为0.01.臂架幅度对俯仰力矩系数CMy的影响趋势与其对顺风向系数Cx类似，在各风向角下也相应增大，但增加幅度也减小.这是因为俯仰力矩的主要贡献量是顺风向的力，风向角为45°时增幅最大为0.07.90°风向角时，3种臂架幅度工况下，顺风向的力相同，而臂架不同的俯仰角度导致风载作用在模型上的俯仰力矩不同，因此与顺风向系数Cx不同，数值大小不同.臂架幅度对扭转力矩系数CMz的影响趋势与顺风向系数Cx和俯仰力矩系数CMy的趋势刚好相反，臂架俯仰角增大，扭转力矩系数CMz减小，臂架俯仰角由20°增加到60°的减小幅度小于由60°到80°的减小幅度.臂架俯仰角度增大，Cy，CMx的绝对值略微增加，但大致趋势相同，均在零值上下波动.升力系数Cz在3种臂架幅度下都在均值0.04上下浮动.

4.3 不同地貌的影响

风场地貌类型总共有A类和B类两种，分别对应臂架幅度为20°，60°和80°三种俯仰角度，试验数据表明臂架幅度为20°，60°和80°时，风场地貌对风载荷基底响应均值的影响趋势类同.这里仅以臂架幅度为20°为例进行结果分析及讨论.臂架幅度为20°时，不同风场地貌的基底力响应均值的无量纲系数Ci随风向角的变化情况如图7所示，力矩基底响应均值的无量纲系数CMi随风向角的变化曲线如图8所示.

图7 20°臂架俯仰角不同风场地貌各风向角Ci曲线Fig.7 Civs.wind inlet angle of varies wind field type with boom luffing angle 20°

图7和图8表明，两种风场地貌下顺风向系数Cx在75°风向角时大小发生交替.0°～75°风向角时，B类顺风向系数Cx大于A类，0°风向角时最大差值max（ΔCx）为0.011；75°～180°风向角时，B类顺风向系数Cx小于A类，135°风向角时最大差值max（ΔCx）为0.015；所有风向角下，B类地貌的Cy，Cz都大于或等于A类地貌的Cy，Cz最大差值max（ΔCx），max（ΔCz）分别在风向角＝15°时为0.013和风向角＝75°时为0.012；A类风场地貌的力矩系数CMx，CMy，CMz都略大于B类风场地貌，差值不超过0.005.在90°风向角时，CMx，CMy，CMz在两种地貌下数值均相等.由上述分析可知，相较于不同风向角、臂架幅度对风载荷的基底响应均值的影响程度，不同地貌下基底响应均值的差异较小.

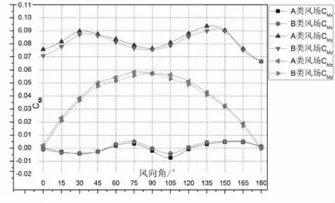
图8 20°臂架俯仰角不同风场地貌各风向角CMi曲线Fig.8 CMivs.wind inlet angle of varies wind field type with boom luffing angle 20°

4.4 危险工况讨论

7 500t浮式起重机在不同幅度下，风力系数的最大值及其所对应的风向角见表2.

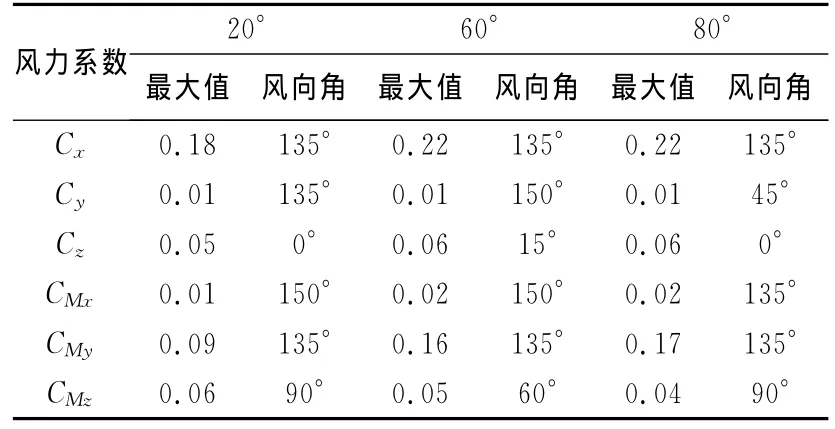
表2 不同臂架幅度下7 500t浮式起重机风力系数表Tab.2 Wind coefficient of 7 500tfloating crane vs.different luffing angle

由表2可知，随着臂架俯仰角增大，风力系数逐渐增大.风载荷在沿臂架方向最明显，当风向角在135°附近时达到最大值.且随着臂架俯仰角增大，增大显著.风载荷引起的倾覆力矩在绕垂直于臂架的y轴方向最明显，且当风向角在135°附近时达到最大值.

5 结 论

1）基底响应均大致关于90°风向角对称或反对称.等轴侧方向（135°风向角）浮吊的实际风载荷达到最大，若只沿主轴方向（90°风向角）进行结构或整机风载荷稳定性校验，则可能漏掉整机实际最大风载荷.

2）臂架俯仰角度增大，臂架的迎风面积也增加，结构迎风面积的变化是不同臂架幅度下基底响应不同的主要原因.

3）开阔海域的A类地貌和近岸海域的B类地貌下基底响应的差异较小.

通过高频动态天平测力风洞试验，全面研究了不同风向角、臂架幅度及风场地貌对7 500t浮吊风载荷特性的影响机理，为巨型浮吊的风载荷计算提供了试验依据.

［1］郑惠强，申静静，张氢.7 500t浮式起重机臂架钢结构分析［J］.中国工程机械学报，2008，6（2）：184－187.ZHENG Hui－qiang，SHEN Jing－jing，ZHANG Qing.Steel structure analysis on boom of 7500tfloating crane［J］.Chinese Journal of Construction Machinery，2008，6（2）：184－187.（In Chinese）

［2］董达善，王晟，梅潇.7 500t浮式起重机风载荷计算［J］.上海海事大学学报，2009，30（4）：6－9.DONG Da－shan，WANG Sheng，MEI Xiao.Wind load calculation of 7 500tfloating crane［J］.Journal of Shanghai Maritime University，2009，30（4）：6－9.（In Chinese）

［3］李正农，郝艳峰，刘申会.不同风场下高层建筑风效应的风洞试验研究［J］.湖南大学学报：自然科学版，2013，40（7）：9－15.LI Zheng－nong，HAO Yan－feng，LIU Sheng－hui.Wind tunnel test of tall building wind effect in different geomorphologic terrain categories［J］.Journal of Hunan University：Natural Sciences，2013，40（7）：6－9.（In Chinese）

［4］TSCHANZ T，DAVERPORT A G.The base balance technique for the determination of dynamic wind load ［J］.Wind Engineering ＆Industrial Aerodynamics，1983，13：429－439.

［5］COOK N J.A sensitive 6－component High－frequency－range balance for building aerodynamics［J］.Journal of Physics E：Scientific Instruments，1983，16（5）：390－393.

［6］肖正直，李正良，汪之松，等.基于高频天平测力试验的输电塔风载荷空间分布估计［J］.华南理工大学学报：自然科学版，2009，37（6）：147－152.XIAO Zheng－zhi，LI Zheng－liang，WANG Zhi－song，et al.Spatial distribution estimation of wind loads on transmission tower based on high－frequency force balance tests［J］.Journal of South China University of Technology：Natural Science Edition，2009，37（6）：147－152.（In Chinese）

［7］SIMIU E，SCANLAN H R.Wind effects on structures and introduction to wind engineering［M］.2nd ed.New York：John Wiley ＆Sons，1995：191－195.

［8］CERMAK J E.Advances in physical modeling for wind engineering［J］.Journal of Engineering Mechanics，1987，113（5）：737－756.

［9］黄鹏，顾明，全涌.高层建筑标准模型风洞测压和测力试验研究［J］.力学季刊，2008，29（4）：627－633.HUANG Peng，GU Ming，QUAN Yong，Wind tunnel test research on CAARC standard tall building model［J］.Chinese Quarterly of Mechanics，2008，29（4）：627－633.（In Chinese）

［10］WHITE F M.Fluid mechanics［M］.5th ed.New York：McGraw－Hill，2012：293－296.