考虑直流控制的直流输电线路短路电流变化特性研究

蔡泽祥，徐 敏，李晓华，辛镇瀚

（1.华南理工大学 电力学院，广东 广州 510640；2.中国南方电网超高压输电公司广州局，广东 广州 510405）

0 引言

传统交流电网短路电流严格服从电路物理定律，形成了完备的故障计算与继电保护分析方法体系。然而，直流输电线路短路电流不仅受电路物理定律约束，还具有与直流控制系统强相关的特点，随故障位置和故障时刻不同，直流线路短路电流变化特性存在差异，反映出短路电流复杂的时空关联特性。目前，对于考虑控制作用的直流线路短路电流变化特性尚未形成清晰明确的结论，给直流线路故障分析和继电保护运行等带来了阻碍[1-2]。

由于与直流控制强相关，并且受到故障条件、线路分布参数、末端设备等影响，直流线路短路电流变化特性较为复杂。目前，工程界主要采用数值仿真方法，基于PSCAD/EMTDC、RTDS等工具反复试验开展研究[3-5]。一方面，数值仿真的有效性极大地依赖于详细的直流控制模型及参数，其结论往往缺乏普适性，难免限于一时一地的具体案例分析；另一方面，数值仿真结果使得短路电流的变化规律以及直流控制的作用机理被淹没于海量的数值仿真计算之中，难以建立完备的分析方法体系[6-8]。

鉴于此，相关研究工作试图从解析方法角度开展直流线路短路电流的研究，以揭示其变化规律及各因素的影响机理。文献[9-11]推导了换流器直流侧出口短路时短路电流的解析表达式，然而由于直流线路简单地采用集中参数模型，所得解析结果与实际直流线路短路电流存在较大差异。文献[12]考虑了直流线路的分布参数特性，但所得解析表达式过于复杂，不能够直接用于短路电流变化特性的分析，文中也未考虑直流控制系统对于短路电流变化特性的影响。

本文推导了考虑分布参数特性的直流线路固有短路电流的时域解析表达式，分析了直流线路短路电流的固有变化特性。从直流控制对短路电流变化的影响机理出发，揭示了考虑控制作用的短路电流幅值时空变化特性。结合直流线路保护电流变化量判据的工作原理，探讨了直流线路短路电流幅值时空变化特性对于判据整定计算的影响。

1 直流线路固有短路电流解析

1.1 直流线路故障暂态与解析模型

直流输电线路长度通常在1000 km以上，具有典型的分布参数特性。直流线路发生故障后，故障点的电流产生阶跃突变，并以行波形式沿线路向两端换流站传播。到达线路两终端后，经过换流站设备反射改变方向，继而沿线路流向故障点。这一反射波到达故障点后，将被再次反射，如此周而复始。故障电流行波在线路其中一端与故障点间的传播过程（过渡电阻为零的理想故障条件下）可用图1的网格图表示。

图中，Td为行波在故障点与终端之间往返一次所需要的时间，与故障距离Lf相关；Iinci为由故障点流向终端设备的电流行波；Irefi为由终端设备流向故障点的电流行波；Ii（s）为构成短路电流的第i个分量，由 Iinci（s）和 Irefi（s）叠加而成，所有 Ii（s）之和即为实际短路电流[13-14]；i=1，2，…，n。

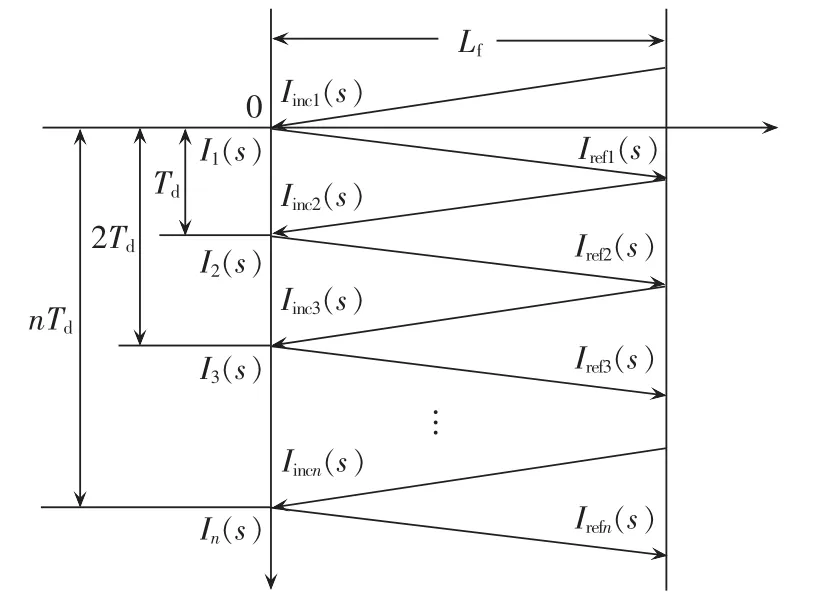
图1 故障电流行波传播网格图Fig.1 Transmission of fault current traveling wave

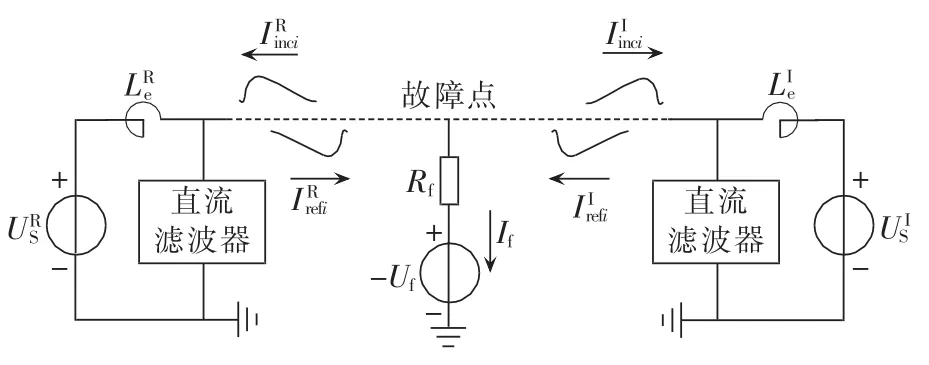
图2 直流输电系统线路故障等效网络Fig.2 Equivalent circuit of HVDC system for line fault

直流输电系统在线路故障后的等效故障网络如图2所示。图中，URS和UIS分别为整流侧和逆变侧的等效电压源；LRe和LIe分别为整流侧和逆变侧平波电抗器电感与等效电压源内电感之和；Rf为故障点过渡电阻；Uf为故障点稳态电压。

由于线路参数的频变特性、直流控制的强非线性，难以对短路电流进行精确的时域解析[15]。本文对直流输电系统线路故障模型进行如下简化，以求取短路电流的解析表达式：直流控制作用进行单独考虑；不考虑直流滤波器的影响；直流线路无损、无畸变；故障点过渡电阻为零；仅考虑直流输电系统的故障分量。简化模型保留了直流线路分布参数的基本特征，包含了故障端口、线路终端设备等关键因素，因此，基于简化模型进行短路电流固有变化特性解析分析，所得结论具有一般性。

1.2 固有短路电流的时域解析

如图1所示，第一个入射波到达线路终端前（t＜0），流入平波电抗器的故障电流为零。第一个入射波到达线路终端后（0≤t≤Td），流入平波电抗器的电流由I1（s）决定；第二个入射波到达终端后，流入平波电抗器的电流除了I1（s）外，还需要在其上叠加I2（s）。依此类推，流入平波电抗器的电流实际上由n个分量叠加而成，n值由计算时间tcal和故障距离共同决定。若以故障行波第一次到达线路终端时刻为时间零点，则有故障电流复频域表达式如下：

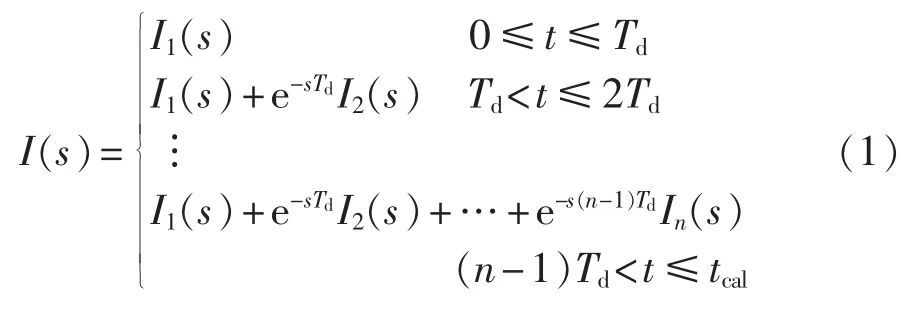
其中，n=floor（tcal/Td），floor（·）函数是指对参数沿绝对值减小的方向向下取整。

从上式可以看出，推导I（s）的关键在于求取各个分量 Ii（s），下面分别求取之。

a.求 I1（s）。

根据行波在线路终端的折反射规律[15]，Iref1（s）与Iinc1（s）的关系如下：

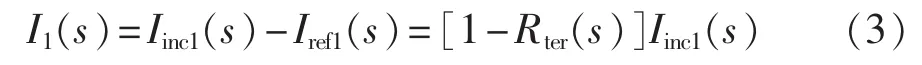
b.求 I2（s）。

根据行波在故障点的折反射规律[15]，Iref1（s）与Iinc2（s）的关系如下：

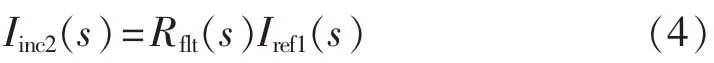
其中，Rflt（s）=-1，为行波在故障点的反射系数。

将式（2）代入式（4）可得：

进一步参考式（2）和（3）的推导过程，可得 I2（s）的表达式如下：

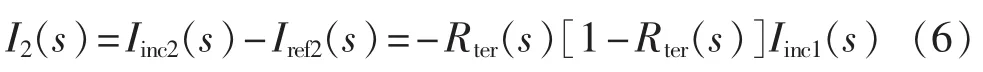
c.求 Ii（s）。

依此类推，可以得到Ii（s）的表达式如下：

为不失一般性，假设故障点初始电流阶跃行波Iinc1（t）为单位阶跃函数，其拉氏变换 Iinc1（s）为 1 /s。将Rter（s）和 Iinc1（s）的表达式代入式（7）可得：

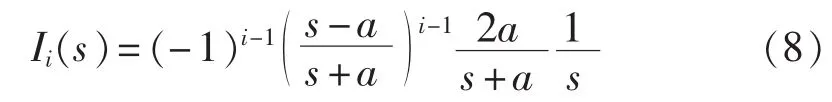
至此，得到了Ii（s）的一般表达式。下面进一步推导 Ii（t）的表达式。

对式（8）进行部分分式展开：

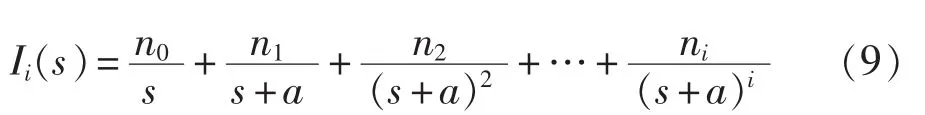
求式（9）的拉氏反变换，得到 Ii（t）如下：

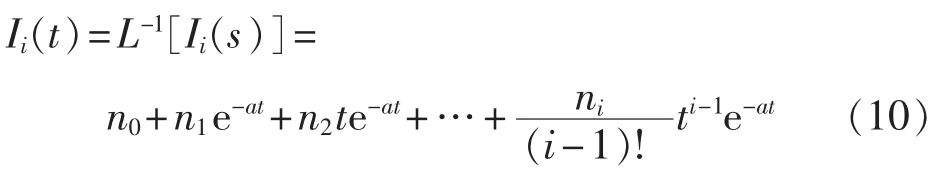
综合式（1）和（10）即可得在计算时间tcal内任意时刻线路一端的故障电流时域表达式为：

2 直流线路短路电流的固有变化特性

2.1 Ii（t）波形特征与变化规律

当 i取 1、2 时，根据式（8）和（9）容易得到 I1（s）和 I2（s）分别为：

求其拉氏反变换，得到 I1（t）和 I2（t）为：

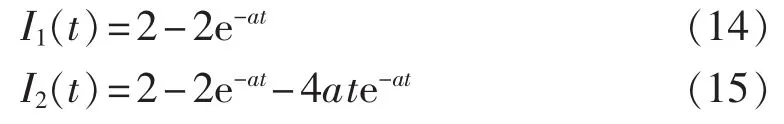
更高次入射波和反射波形成的电流分量Ii（s）表达式比较复杂，一般可利用MATLAB或Maple计算软件中的符号计算功能进行时域表达式的求取。

根据 Ii（t）时域表达式，画出 I1（t）—I8（t）（均为标幺值）的波形如图3所示，其中a取2000s-1，计算时间tcal取 12 ms。 对其进行分析，可以得到 Ii（t）的波形特征与变化规律如下：

a.Ii（t）总体呈上升趋势，经过有限次的振荡，最终均趋向于稳态值2，即初始入射波幅值的2倍；

b.对于给定的 i，Ii（t）的振荡次数是确定的，且随着i的增大，振荡次数逐渐增多；

c.i越小，Ii（t）达到稳定值所需的时间越短，反之所需时间越长；

d.对于同一个 Ii（t），起始振荡幅度一般较小，随着计算时间的增加，振荡幅度逐渐增大。

图3 I1（t）—I8（t）的时域波形Fig.3 Time-domain waveforms of I1（t）-I8（t）

通过对更高次Ii（s）进行拉氏反变换并绘制波形图，可以证明上述规律的普遍性，此处不再赘述。

2.2 短路电流的固有变化特性

从式（11）及 2.1 节可知，I（t）实际上是由 I1（t）、I2（t）、…、In（t）的波形叠加而成，其中 n 值由故障距离和计算时间共同决定。以tcal=6 ms、Lf=120 km（对应 Td=0.8 ms）为例，a 取 2000 s-1时，I（t）（标幺值）的波形图如图4所示。

图4中，在每个区段 I（t）都由多个 Ii（t）叠加而成，且随着时间的推移叠加分量逐渐增多。从图中可以看出，I（t）具有振荡上升的特性：总体上呈上升趋势，但在某些时间段有可能出现暂时性的下降，如图中虚线椭圆所示。

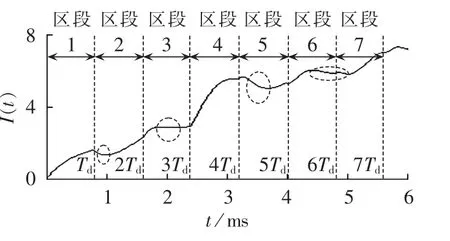
图4 故障距离120 km时的短路电流Fig.4 Short circuit current of 120 km line fault-distance

下面对线路近端故障和远端故障2种极端情况下的短路电流进行分析，以进一步明确短路电流变化的一般规律。

当线路近端故障时，以Lf=0 km为例，根据集中参数电路计算理论，平波电抗器端电压的计算式为I（s）sLe；根据行波理论，线路首端短路时，故障点电压计算式为Iinc1（s）Zc。考虑到平波电抗器端点和故障点为同一点，因此有下式成立：

求解式（16）可得：

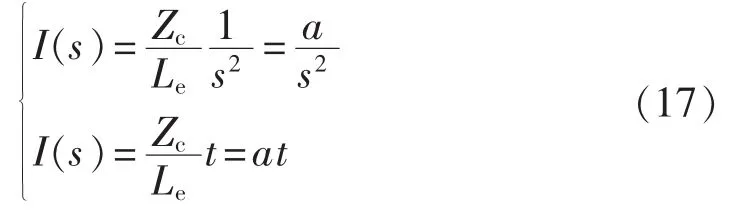
当线路首端短路时，短路电流是斜率为a的直线。

在线路远端故障时，若所关心的时间域相对较小，则有可能出现 I（t）始终仅由 I1（t）构成的情况，此时结合式（14）有：

故线路远端短路时，短路电流是一终值为2的指数曲线。

综合上述3种情形下电流波形，可以得到直流输电线路短路电流I（t）振荡上升的固有变化特性：近端故障时，有限时间内短路电流的振荡次数趋向无穷，短路电流几乎成直线上升；随着故障距离的增加，有限时间内短路电流的振荡次数逐渐减少，短路电流总体上仍呈上升趋势；当故障距离足够大时，在关心的时间域内，短路电流呈振荡次数为零的指数上升。直流线路短路电流总体上随故障持续时间增加而逐渐上升，近端故障时的短路电流要大于远端故障时的短路电流，符合短路电流发展的时间约束和物理边界条件约束。

3 考虑直流控制的短路电流变化特性

上文利用解析法分析得到了直流线路短路电流的固有变化特性，本节进一步分析考虑直流控制作用的短路电流变化特性。直流控制系统包含有复杂的滤波、比较、非线性变换等环节，难以对其进行直接解析分析[15]。本文根据直流线路短路后定电流控制动作降低短路电流这一作用效果，分析其对短路电流固有变化特性的影响机理，并采用PSCAD/EMTDC详细模型进行仿真验证，为直流线路保护电流判据研究提供指导。

3.1 考虑直流控制的短路电流空间变化特性

故障行波传输到线路终端后，经过一定的动作延时，直流控制系统动作抑制故障电流增长。设控制系统动作延时为tctr，则结合短路电流的固有变化特性可得含控制作用时不同故障距离下的短路电流波形示意图如图5所示。

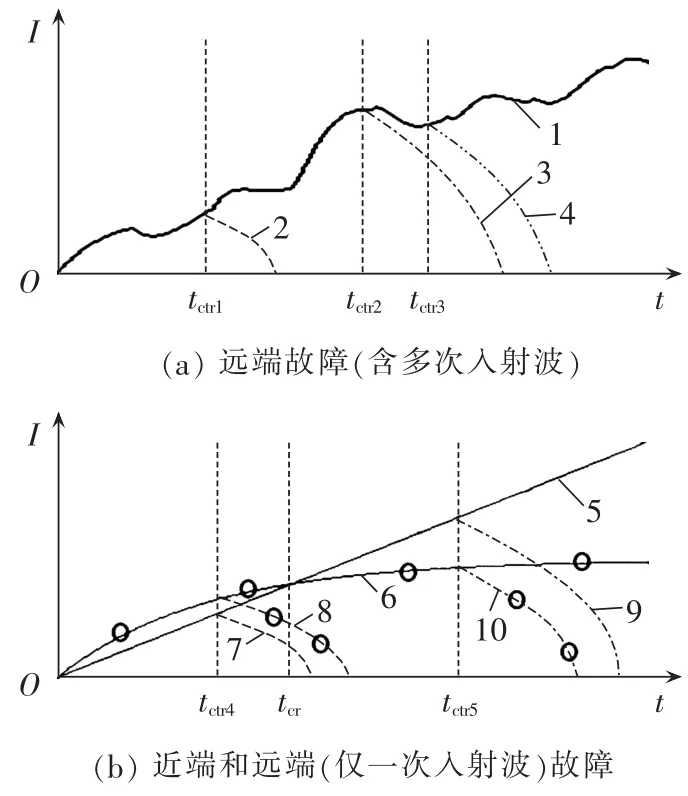
图5 含控制作用短路电流示意图Fig.5 Schematic diagram of short circuit currents under control

图5中，曲线1、5、6为不含控制作用时的短路电流波形，剩余7条曲线为含控制作用时的短路电流波形（示意图）；tctr1、tctr2、…、tctr5表示控制系统响应延时；tcr为曲线5和6的相交时刻，由于曲线5斜率始终为a，曲线6的斜率初始为2a、终止为0且单调减小，因此tcr必然存在。

分析图5（a）可得，控制系统作用能够抑制短路电流的增长。由于短路电流振荡上升的固有变化特性，短路电流幅值随着控制延时的增加非严格单调递增，如曲线3和4所示。

从图 5（b）可以看出，当 tctr=tctr4＜tcr时，输电线路远端短路电流始终大于近端短路电流，远端短路电流幅值大于近端短路电流幅值；当tctr=tctr5＞tcr时，输电线路远端短路电流初始阶段大于近端短路电流，过了tcr后小于近端短路电流，且远端短路电流的幅值较近端要小。

实际上，由于短路电流的振荡上升特性，不同故障距离下的短路电流曲线往往有多个交点。图6为根据式（11）画出的 0 km和 120 km处故障时 I（t）（标幺值）的波形，其中取 a=1000 s-1，tcal=6 ms。 可以看出，在 tctr＜tctr1和 tctr2＜tctr＜tctr3区域内，均有 120 km短路的故障电流幅值大于0 km短路的故障电流幅值，如图中虚线椭圆所圈示部分。

图6 不同故障距离下故障电流波形Fig.6 Waveform of short circuit current for different fault-distances

传统上，一般认为直流线路短路电流幅值随故障距离增加而单调递减，在近端故障时最大、在远端故障时最小。从上文分析可以看出，当直流控制动作延时满足一定条件，直流线路短路电流幅值随故障距离增加表现出非单调减小的变化特性，这突破了传统短路电流变化特性的空间认识局限。

3.2 考虑直流控制的短路电流时间变化特性

在包含换相过程的实际直流输电系统中，控制系统通过增大换流阀触发角来抑制故障电流。触发角增大后，故障电路相当于交流系统的相间短路[15]，短路电流开始时逐渐增大，达到由故障电路所决定的最大值后逐步减小，从而实现故障电流的抑制。

以六脉桥换流器为例，不考虑换相过程。若故障行波于t0时刻到达线路终端，控制延时为tctr，则控制作用时刻 tact=t0+tctr。 不妨设 t1＜tact＜t2，即控制系统开始作用时刻换流器处于阀V1和V2导通状态，此时换流器出口电压和等效故障电路分别如图7（a）和图7（b）所示。设电路功率因数角对应的时域值为tα，则故障电流的总上升时间ttot为：

其中，t3为线电压eac的峰值时刻。

在t1＜tact＜t2区间内，随着故障时刻t0的增大，tctr渐近趋向于t2。在此过程中，故障电流上升时间ttot逐渐减小，因此故障电流幅值也逐渐减小。当tact达到t2时，故障电路发生跃变，转为阀V2和V3导通状态，等效故障电路如图7（c）所示。

在阀V3导通瞬间，故障电流上升时间和故障电流幅值发生跃变，其值与tact=t1时相等。图8给出了在PSCAD/EMTDC环境下，基于某实际直流系统模型，仿真得到的直流线路首端单相接地短路故障电流幅值随故障时刻的变化曲线。

传统直流线路短路电流幅值计算主要参考交流电网短路电流计算方法进行，并未考虑故障时刻对短路电流幅值的影响。从图8可以看出，在直流系统中，由于控制系统作用，短路电流幅值具有明显的时间离散变化特性，随故障时刻不同表现出锯齿状变化规律，这突破了传统短路电流变化特性的时间认识局限。

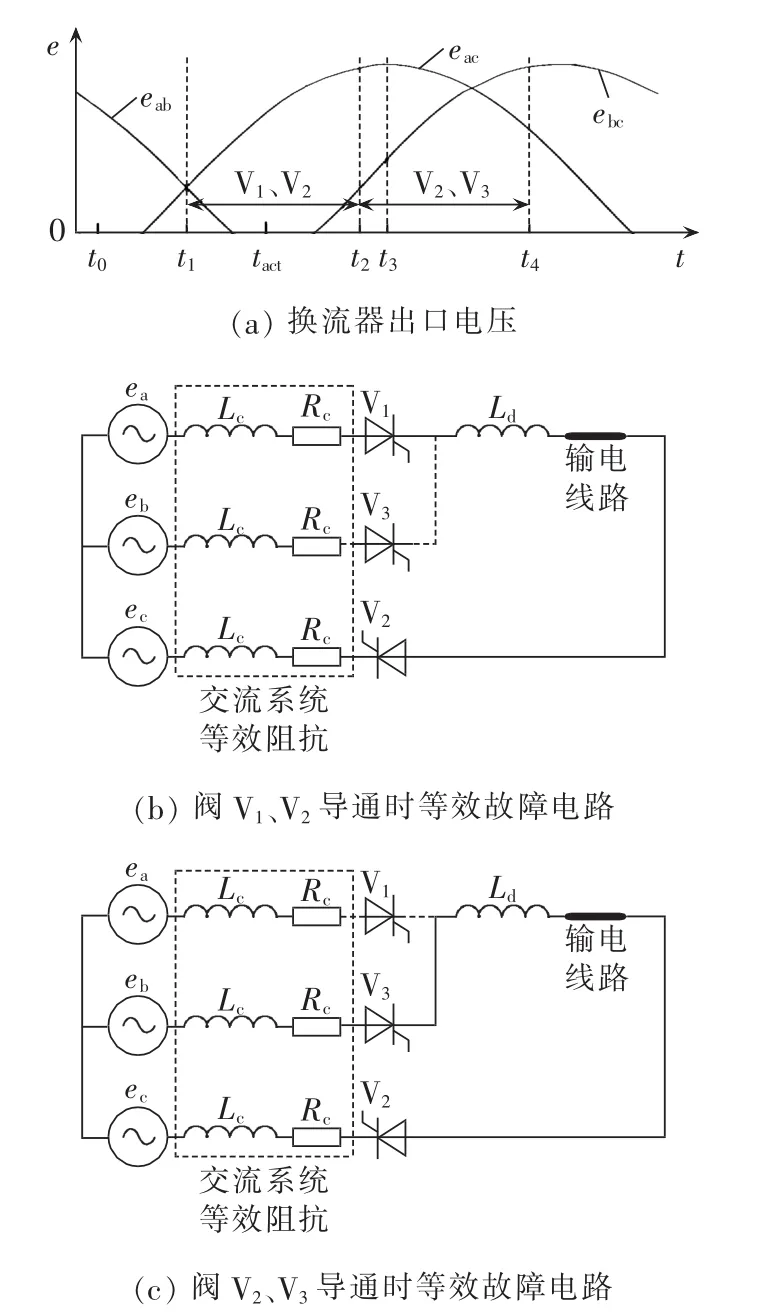
图7 短路电流幅值随故障时刻变化原理Fig.7 Schematic diagram of short circuit current magnitude varying with fault time

图8 不同故障时刻下的短路电流幅值Fig.8 Curve of short circuit current magnitude vs.fault time

3.3 短路电流时空特性对继电保护的影响

直流线路保护中，电流变化量判据通过检测直流线路短路电流相对于稳态电流的变化量进行区内和区外故障判别。在电流变化量判据整定计算中，需要确定区内故障时保护特征量的最小值和区外故障时保护特征量的最大值，以保证判据的选择性。

由于短路电流幅值的空间非单调变化特性，区内故障时保护特征量的最小值不一定出现在直流线路终端短路情况之下，因此不能简单地选取直流线路终端短路时的电流变化量幅值作为保护特征量的整定边界。由于短路电流幅值的时间离散变化特性，区外故障时保护特征量的最大值应选取锯齿波的顶点，区内故障时保护特征量的最小值应选取锯齿波的底端。

4 结论

本文利用解析法分析了考虑控制作用的直流线路短路电流变化特性，得到的主要结论如下。

a.直流线路短路电流具有振荡上升的固有变化特性，其总体趋势逐渐上升，近端故障时的短路电流要大于远端故障时的短路电流，符合短路电流发展的时间约束和物理边界条件约束。

b.在直流控制作用下，直流线路电流幅值具有空间非单调变化特性和时间离散变化特性。空间上，短路电流幅值随故障距离增加非单调减小；时间上，短路电流幅值随故障时刻不同表现出锯齿状变化规律。

c.直流线路保护电流变化量判据整定计算中，不能简单地选取直流线路终端短路时的电流变化量幅值作为保护特征量的整定边界；区外故障时保护特征量的最大值应选取锯齿波的顶点，区内故障时保护特征量的最小值应选取锯齿波的底端。

d.需要指出的是，本文解析分析虽然采用的是未考虑行波色散、过渡电阻的理想模型，但所揭示的直流控制作用导致的直流线路短路电流变化时空关联特性及其对继电保护的影响结论却与以上因素无关，具有一般性。