双馈风电场阻尼系统次同步振荡的无功功率控制策略

李 辉，陈耀君，赵 斌，刘盛权，杨 东，杨 超，胡姚刚，梁媛媛

（1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044；2.重庆科凯前卫风电设备有限责任公司，重庆 401121）

0 引言

近年来，随着电力系统中高电压、大容量、远距离输电工程的实施，为了提高线路传送能力及改善电力系统的静态稳定性，常对输电线路进行串联电容补偿，但在一定条件下也易激发电力系统次同步振荡SSO（Sub-Synchronous Oscillation）[1]。 同时随着大容量风电场规划和实施，特别是风火打捆输电项目的建设，风电场或风电场群与接入的电力系统中汽轮发电机组的相互作用和影响也随之加大[2-4]。在风火打捆输电方式下，含大容量风电场的电力系统发生次同步振荡时，将会造成同步电网中汽轮发电机组轴系扭振以及大容量风电场的风电机组不稳定。因此，如何从提高电力系统稳定性以及风电机组安全运行的角度，研究含风电场电力系统次同步振荡的阻尼控制策略，无疑对风火打捆输电系统的安全稳定运行有着重要现实意义。

目前，随着大功率电力电子技术在电力系统中的广泛应用，国内外学者对如何利用各种不同功能的柔性交流输电（FACTS）设备抑制电力系统次同步振荡展开诸多研究，其中以加装静止无功补偿器（SVC）、可控串联补偿（TCSC）和静止同步补偿器（STATCOM）等无功补偿装置抑制次同步振荡的研究较为热门。文献[5-8]均利用汽轮发电机转速偏差信号作为控制信号设计阻尼控制策略，控制SVC、STATCOM向系统注入与模态频率互补的次同步电流分量抑制次同步振荡。对于现有的风火打捆输电系统，上述成果能为抑制次同步振荡提供较好的研究思路，但对于上述系统，其本身含有快速独立无功功率控制能力的双馈风电场，能否在不增加附加二次设备的情况下通过设计风电场控制策略阻尼系统次同步振荡，这一课题思路值得深入研究。文献[9]详细地分析了无功发生源抑制电力系统次同步振荡的机理，虽然文献利用复转矩系数法推导了无功发生源向发电机提供的附加电气力矩的增加量，但是对于含双馈风电场的多机系统，复转矩系数法已不再适用。文献[10-14]依据特征值计算和时域仿真方法研究，提出通过风电场无功附加控制策略可对电力系统的阻尼起改善效果，虽然文献得出了DFIG无功功率控制对阻尼的作用效果，但是并未给出其阻尼形成机理、阻尼的性质以及电气阻尼系数大小。文献[15-16]基于双馈风电场无功功率环设计了附加阻尼控制策略，虽能有效提供系统正阻尼，但是文中并未分析风电场无功功率提供正阻尼的条件以及设计控制策略的依据，也未分析可能导致风电机组自身轴系扭振等的安全稳定性问题。因此，分析双馈风电场无功功率对系统贡献的阻尼大小和性质以及如何利用双馈风电场设计有效抑制次同步振荡的控制策略还有待进一步研究。

本文利用双馈风电机组转子侧变流器无功功率控制，引入无功-转速型传递函数，推导了双馈风电场无功功率对系统贡献的阻尼系数大小和性质的表达式，并基于分析获得的提供系统正阻尼条件，利用遗传算法优化设计含PID相位补偿环节的附加阻尼控制策略抑制次同步振荡。最后，以双馈风电场接入 IEEE第一标准测试系统为例，对双馈风电场无功功率附加阻尼控制时的系统运行性能进行仿真和比较分析。

1 双馈风电场抑制次同步振荡的机理研究

1.1 含双馈风电场并网的系统方案

含双馈风电场的IEEE第一标准测试系统如图1所示。其中，G表示汽轮发电机组，C表示双馈风电场，D表示汽轮机轴系六质量块弹簧模型，以风火打捆方式经500 kV线路传输电能至无穷大电网E；RL+jXL表示输电线路阻抗；XC、Xsys分别表示串联补偿电容的容抗和无穷大系统连接线路电抗。假设风电场内各台风机运行状态相同，采用容量等值方法对风电场进行单机等值。

1.2 基于风电场无功功率阻尼次同步振荡的分析

为了分析双馈风电场对系统阻尼影响的机理，将系统方案简化，如图2所示。图中，E为汽轮发电机G的q轴暂态电势；UA为双馈风电场接入端电压；UB为无穷大母线电压；δ、γA分别为 E、UA与 UB之间的相角差；Pe、Qe分别为汽轮发电机端输出有功和无功功率；Pg、Qg分别为双馈风电场端口输出有功和无功功率；PL、QL分别为汽轮发电机与双馈风电场并联端口输出有功和无功功率；X1、X2为线路电抗参数。

汽轮发电机输出的有功功率Pe、无功功率Qe可以分别表示为：

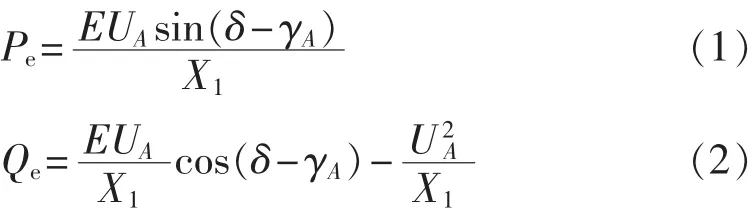
为了简化分析，认为双馈风电机组向电网注入的无功功率Qg仅引起母线电压UA的微小幅值变化，增量为ΔUA。假设汽轮发电机组Δω发生幅值为A、频率为 ω0的微变，分别对式（1）、（2）进行偏差化分析可得：

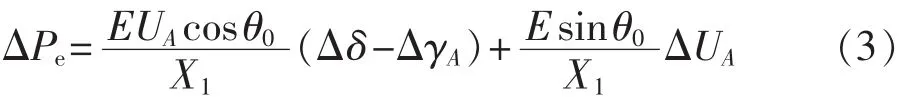
图1 系统结构图Fig.1 System structure

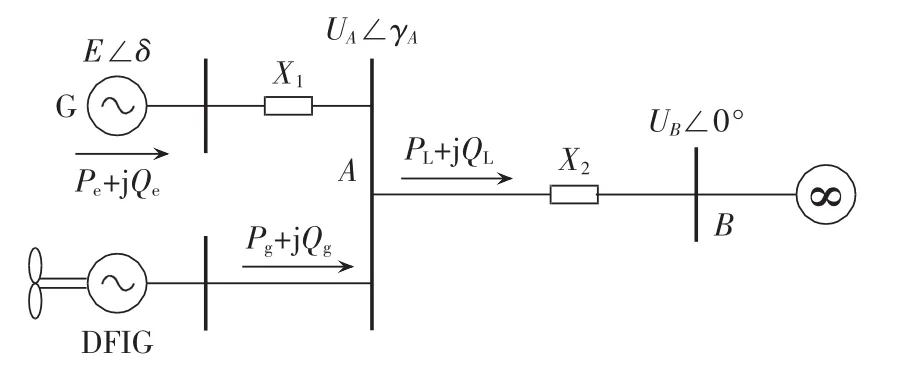
图2 系统简化示意图Fig.2 Simplified diagram of system

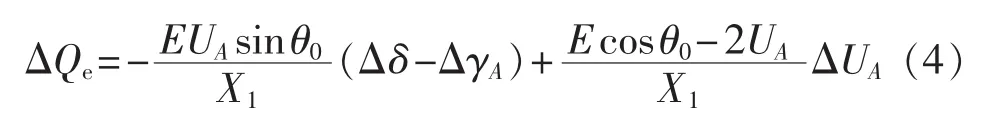
其中，θ0=δ0-γA0，下标 0 均表示初值。 由于 ΔQg引起母线电压UA变化可得：

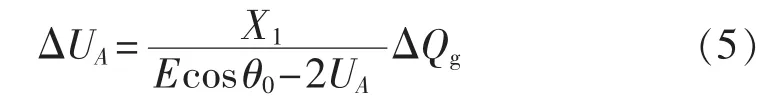
根据有功功率线路功率平衡关系，化简整理得：

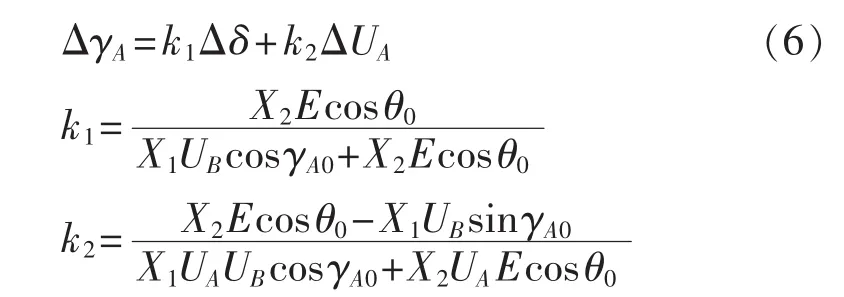
将式（5）、（6）代入式（3），得到轴系产生的电磁转矩增量：

为了分析风电场无功功率Qg对系统次同步振荡的阻尼性质，本文引入转速与无功功率的传递函数GωQ（s）（简称无功-转速型传递函数），即同步发电机转速ω（s）和风电场输出无功功率Qg（s）的传递函数：

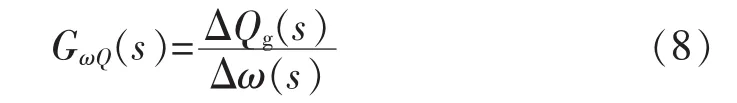
由汽轮发电机组Δω发生幅值为A、频率为ω0的微变可得：

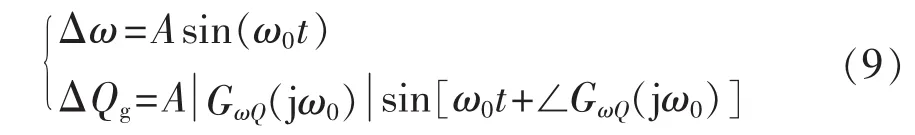
同时为了分析式（7）最后一项的阻尼作用大小，定义ΔQg在Δω轴上的分量为无功型阻尼系数DωQ：

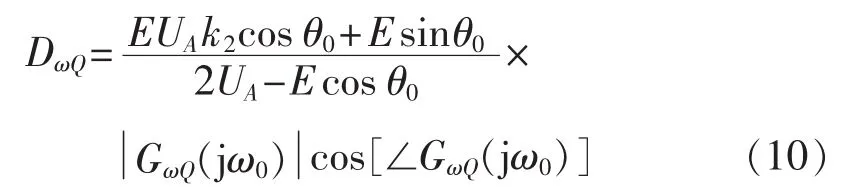
由此可见，当无功-转速型传递函数的相位角范围满足-π/2＜∠GωQ（jω0）＜π/2 时，DωQ＞0，且 DωQ正比于。因此，为了使得双馈风电场动态无功ΔQg对汽轮发电机组轴系电气阻尼起正阻尼作用，提高参与系统抑制次同步振荡的能力，需在次同步频段下，满足其无功-转速型传递函数的相位角范围为：

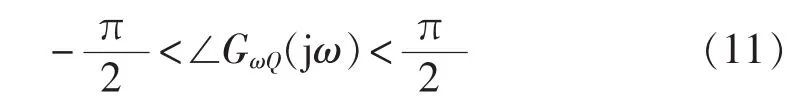
由此可得，当系统发电机轴系的次同步振荡扭振频率为ωi，通过利用发电机转速偏差信号控制风电场输出动态无功ΔQg，满足式（11）在次同步频段相位角范围条件，使得在发电机电枢绕组产生对应于ωi的次同步频率阻尼电磁转矩，则风电场动态无功ΔQg对电气阻尼起正阻尼作用，以此可指导双馈风电场无功功率附加阻尼控制策略设计，从而达到抑制次同步振荡的目的。

2 基于风电场的次同步振荡阻尼控制策略

2.1 次同步振荡附加阻尼控制结构

基于上节机理研究，结合双馈风电机组转子侧变流器能够实现输出有功和无功的解耦控制能力，本文提出风电场转子侧变流器次同步振荡附加阻尼控制策略。以汽轮发电机转速偏差Δω为输入信号，经过适当的处理（延时和滤波），其输出信号ΔUsso可通过无功功率环提供一个附加的动态功率ΔQg，得到双馈风电机组转子侧变流器附加阻尼控制系统原理框图如图3所示。

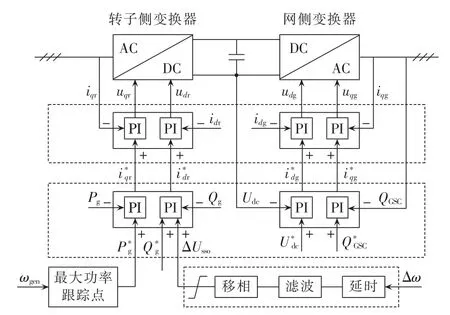
图3 次同步振荡阻尼控制系统原理框图Fig.3 Schematic diagram of SSO damping control system

图中，Pg、Qg分别为风电场输出端的有功功率和无功功率测量值；P*g、Q*g分别为变频器的有功功率和无功功率给定值；id、iq分别为d轴和q轴电流值；ud、uq分别为d轴和q轴电压值；符号中下标r、g分别代表转子侧和网侧；ωgen为风机转速。

延时和滤波环节为信号的预处理环节，本文重点考虑移相环节，考虑到基于PID相位补偿控制器原理结构简单、算法易于实现和鲁棒性强等优点，本节结合上述获得的抑制次同步振荡的相频特性条件，采用PID相位补偿控制器，其相位补偿的传递函数为：

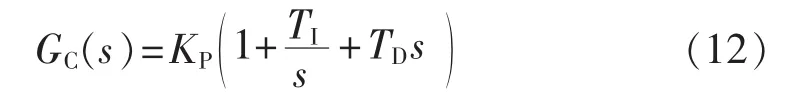
其中，KP为放大增益；TI为积分时间常数；TD为微分时间常数。

在扭振频率ωi下，令补偿相位角φi=∠GC（jωi），则可得，选择合适的控制器参数[17-18]，使得在扭振模态处满足式（11）的相位要求以提供有效正阻尼。

2.2 补偿环节参数优化

为了保证附加阻尼控制器在次同步频段下能提供有效正阻尼作用，首先基于未附加阻尼控制无功-转速型传递函数GωQ（s）分析系统电气阻尼以及初始相角范围，求取其幅频、相频特性以及无功型阻尼系数，如图4所示。由此可以得到在扭振频率ωi处的相角φi；其次基于式（11）提供正阻尼的相角范围，即可得到可补偿的相位角范围[φia，φib]。

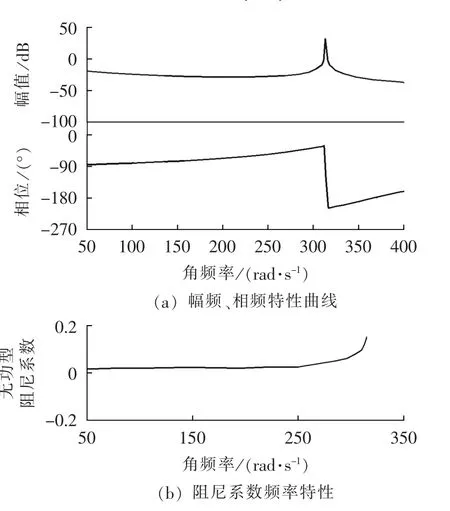
图4 未附加阻尼控制传递函数特性Fig.4 Characteristics of transfer function without additional damping control

为寻求最佳的PID相位控制参数，使得控制器在次同步频段下都能获得最优阻尼控制效果，本文选取以使得闭环系统的特征值最大限度地靠近复平面左侧为目标，其目标函数为：

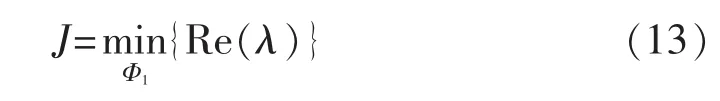
其中，Φ1表示控制器参数（KP、TI、TD）的集合；Re（λ）表示在采用无功功率环附加阻尼控制时扭振模态实部。

采用遗传算法优化的计算流程如图5所示。图中，N1为优化过程迭代总次数。

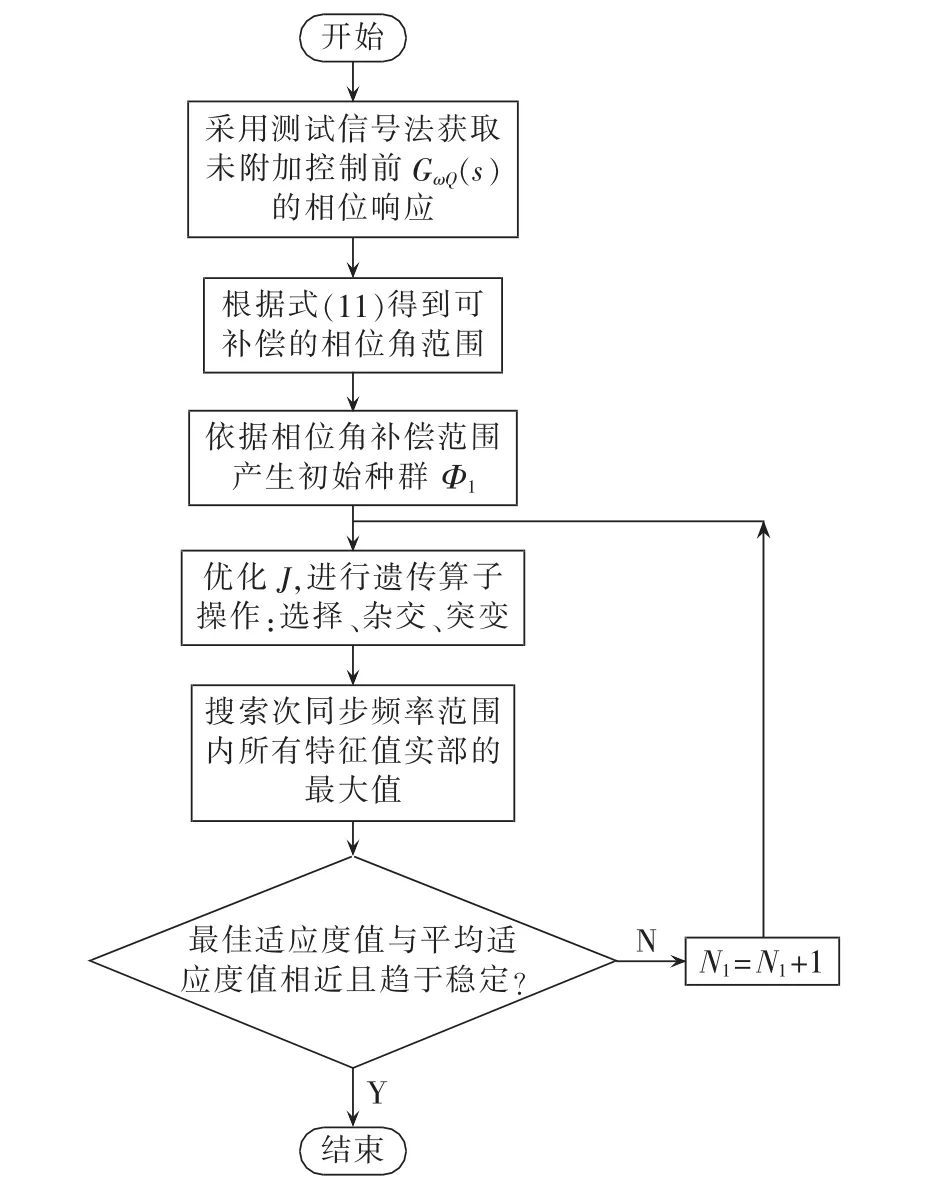
图5 PID控制器参数优化流程图Fig.5 Flowchart of PID controller parameter optimization

本文选定控制参数的取值区间为：KPє（0.1，10），TIє（1，100）ms，TDє（1，100）ms。 根据上述相位补偿控制器参数优化计算流程，计算获得其最佳适应度和平均适应度变化如图6所示。

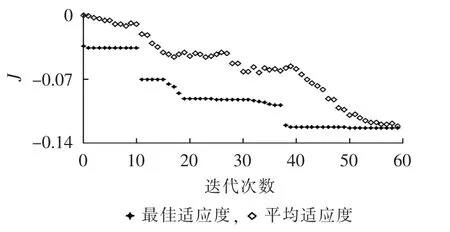
图6 最佳适应度和平均适应度随迭代次数的变化Fig.6 Variation of optimal fitness and mean fitness with iteration times

得出了相位补偿PID控制器参数优化结果：KP=2.5，TI=2.8 ms，TD=5.2 ms。

基于控制器优化参数，可得到其附加阻尼控制策略后无功-转速型传递函数GωQ（s）的幅频、相频特性曲线以及无功型阻尼系数曲线如图7所示。

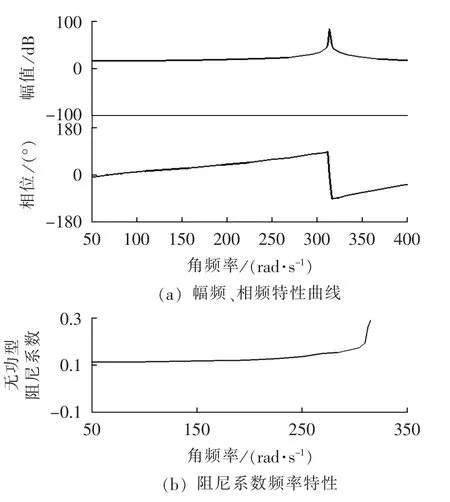
图7 附加阻尼控制下传递函数特性Fig.7 Characteristics of transfer function with additional damping control

通过对比图4和图7可见，引入无功功率环附加阻尼控制后，GωQ（s）的相位角范围处在-π/2～π/2之间，表明阻尼作用为正，保证了整个次同步频段内均能提供正阻尼；无功型电气阻尼系数均为正，且相比于无附加阻尼控制得到显著增加，说明增加无功功率附加阻尼控制策略能有效提高系统电气阻尼。

3 仿真验证

为进一步验证利用双馈风电机组无功功率环附加阻尼控制策略抑制系统次同步振荡的有效性，依据图1系统方案算例，利用DigSILENT/PowerFactory平台进行暂态时域仿真分析。假定0.1 s时在母线B端发生三相短路故障，故障持续时间为0.025 s，即在0.125 s时刻清除故障。仿真系统频率为60Hz，系统中汽轮发电机组容量为892.4MV·A，其轴系有4个呈弱阻尼的扭振模态频率，为15.55 Hz、20.17 Hz、25.40 Hz、31.96 Hz；风电场由100台2 MW双馈风电机组构成，DFIG参数参见文献[19]。IEEE第一标准模型线路参数：输电线路电阻RL=0.02 p.u.，变压器电抗XT=0.14 p.u.，输电线路电抗XL=0.50 p.u.，无穷大系统连接线路电抗Xsys=0.06 p.u.。汽轮发电机参数：纵轴同步电抗 Xd=1.79 p.u.，纵轴暂态电抗 X′d=0.169 p.u.，纵轴次暂态电抗X″d=0.135 p.u.，交轴同步电抗Xq=1.71 p.u.，交轴暂态电抗X′q=0.228p.u.，交轴次暂态电抗X″q=0.2 p.u.，纵轴暂态开路时间常数 T′d0=4.3 s，纵轴次暂态开路时间常数T″d0=0.032 s，交轴暂态开路时间常数 T′q0=0.85 s，交轴次暂态开路时间常数 T ″q0=0.05 s。轴系参数：高压缸惯性系数HHP=0.092897，中压缸惯性系数HIP=0.155 589，低压缸A质量块惯性系数HLPA=0.858 670，低压缸B质量块惯性系数HLPB=0.884215，发电机惯性系数HGEN=0.868495，励磁机惯性系数HEXC=0.0342165。刚度系数：高压缸与中压缸间刚度系数KHP-IP=19.303 p.u./rad，中压缸与低压缸段间刚度系数KIP-LPA=34.929 p.u./rad，低压缸A与B间刚度系数KLPA-LPB=52.038 p.u./rad，低压缸B与发电机间的刚度系数KLPB-GEN=70.858 p.u./rad，发电机与励磁机间的刚度系数KGEN-EXC=2.82 p.u./rad。

图8列出了采用无功功率环附加次同步振荡阻尼控制时系统的运行性能（纵轴各变量均为标幺值），为了进一步比较其抑制效果，图中同时也列出基于常规电力系统稳定器（PSS）有功功率附加阻尼控制以及无抑制措施的结果比较，限于文章篇幅，常规PSS有功功率附加阻尼控制原理框图参见文献[20-21]。

从图8可以看出，与风电场不采用抑制措施相比，采用无功功率附加阻尼控制或有功功率附加PSS阻尼控制均具有较好的抑制次同步振荡效果，汽轮发电机电磁转矩、轴系质量段间扭振响应的振荡不稳定状态均得到了有效的抑制，且无功功率附加阻尼控制的抑制效果要优于有功功率附加PSS阻尼控制。此外，从图8还可以看出，与风电场不采用抑制措施相比，采用附加阻尼控制可使得短路故障后风电机组输出电磁转矩较短时间内达到稳定，但相比于有功功率附加PSS阻尼控制，采用无功功率附加阻尼控制下风电机组转矩波动幅值更小，更易于满足风电机组稳定运行的阻尼特性要求。

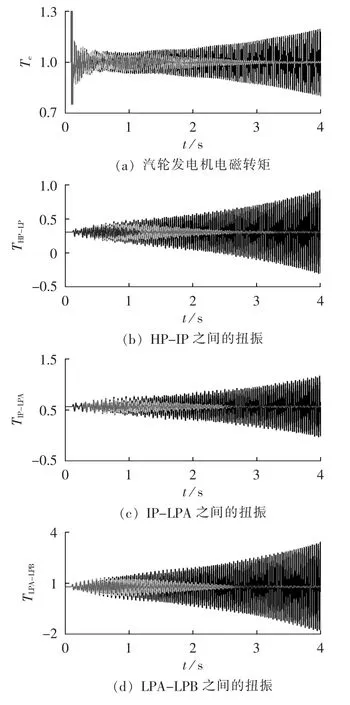
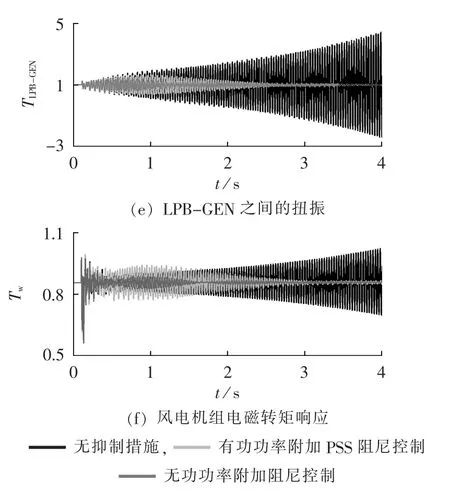
图8 不同阻尼控制时动态性能Fig.8 Dynamic performances for different damping control schemes

4 结论

本文推导并分析了双馈风电场无功功率对系统贡献的阻尼系数大小和性质的表达式，并基于获得的提供系统正阻尼条件，设计了在次同步频段提供最优正阻尼的双馈风电场无功功率环附加阻尼控制策略，所得结论如下：

a.通过引入无功-转速型传递函数，得到风电场无功功率提供正阻尼的范围条件，为分析双馈风电场无功功率对系统次同步振荡的影响和控制系统设计奠定基础；

b.基于获得的提供系统正阻尼条件，利用遗传算法，获得了PID相位补偿环节的优化参数，为在次同步频段范围内提供最优正阻尼的无功功率环附加阻尼控制策略设计提供依据；

c.算例仿真分析进一步验证了本文所提的阻尼控制策略有效性，与有功功率附加PSS阻尼控制策略相比，采用无功功率附加阻尼控制下各质量块扭振幅度以及风电机组转矩波动幅值更小，无功功率环控制的抑制效果更佳。

虽然本文采用遗传算法对PID相位控制器参数进行了优化，但是对于不同相位控制方法及结构对性能的影响还有待进一步研究。