基于可信性理论的含风电电力系统电压稳定概率评估
杨 悦,李国庆,王振浩
(1.华北电力大学 电气与电子工程学院,北京 102206;2.东北电力大学 电力系统安全运行与节能技术国家地方联合工程实验室,吉林 吉林 132012)
0 引言
随着经济的飞速发展,能源问题已经成为人类面临的最严峻问题之一。风能作为清洁可再生能源具有储量巨大、分布广泛且无污染等优点,使得风力发电技术成为目前重要的研究方向之一[1]。而风电接入改变了传统电力系统的结构参数,产生了一些新的问题。
风电接入电力系统后的电压稳定一直是专家关注的难题,因此研究接入风电场后的电力系统静态电压稳定问题是十分必要的。传统的电压稳定分析大多基于确定性模型,而风电的加入使系统模型中节点注入功率具有不确定性。为了解决确定性分析方法无法考虑随机因素影响的问题,研究人员提出了基于概率的电压稳定分析方法。
常用的概率分析方法主要有:蒙特卡洛法、解析法、近似法等。蒙特卡洛法[2-4]通过大量反复抽样仿真来模拟电压稳定分析中节点功率、设备故障等不确定情况,但仿真次数较多、耗时较长;解析法[2,5-7]是采用数学假设对所研究问题进行线性化处理,计算效率较高,其中半不变量法应用较多;近似法[2,8-9]是根据已知随机变量的概率分布,采用近似公式求取待求变量的统计特性,其中以点估计法和一次二阶矩法为代表。以上这些概率分析方法均是在假定了不确定参数的概率统计特征的前提下再进行仿真计算,而不确定参数概率统计特征的准确性会从根本上影响计算的结果。
本文提出对不确定参数进行模糊模拟的可信性电压稳定概率评估方法。该方法不需要假定不确定参数的分布函数类型和参数,就可以对大规模风电并网后的电力系统静态电压稳定问题进行分析。
1 可信性理论
在电力系统这个复杂的物理系统中,许多问题同时包含了随机性与模糊性2类不确定因素,应进行综合性评估。而公理化的模糊性与随机性的综合评估方法就被称为可信性理论[10]。可信性理论是2004年基础数学领域完成的数学分支,它给出了基于测度论的模糊论的公理化体系,并提供了随机性与模糊性综合评估的严格数学基础。
下面对可信性理论中的一些基本概念进行简要说明。
给定一个论域Γ,P(Γ)是Γ的幂集,Pos是一个定义在P(Γ)上的集函数,被称为一个可能性测度。若满足下面的 2 个条件,则称三元组(Γ,P(Γ),Pos)为可能性空间。
b.对于任意的 P(Γ)的子集{AiiєI},其中 I是任意的指标集,有。
基于可能性测度,文献[11]定义了自对偶集函数Cr如下。
定义1 设三元组(Γ,P(Γ),Pos)是一个可能性空间。若定义集函数Cr为:

则称Cr为事件A的可信性测度。其中,A′是集合A的补集。
三元组(Γ,P(Γ),Cr)称为可信性空间[12]。
定义2[12]设三元组(Γ,P(Γ),Cr)是可信性空间。 若 ξ=(ξ1,ξ2,…,ξn)是从 Γ 到实数空间 Rn上的集函数,则称ξ是定义在可信性空间上的模糊向量。特别地,当n=1时,ξ称为模糊变量。
定义3[13]设 ξ1、ξ2、…、ξn是定义在可信性空间(Γ,P(Γ),Cr)上的模糊变量。 若对于 P 上的任意子集 B1、B2、…、Bn满足:

则认为模糊变量 ξ1、ξ2、…、ξn相互独立。 其中,γ 表示设定的某一事件。
在可信性测度基础上,文献[11]给出了模糊变量期望值算子的定义。若满足:
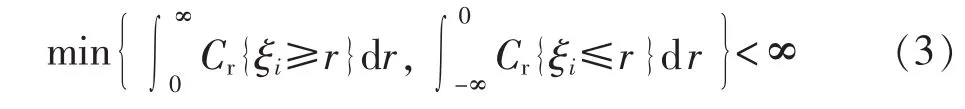
则模糊变量ξi的期望值可以定义为式(4)所示。
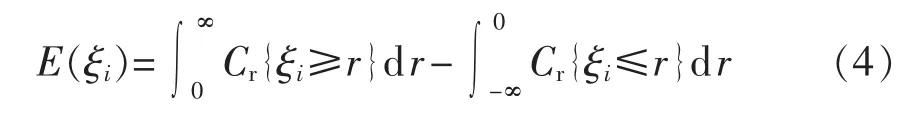
并且,若满足:
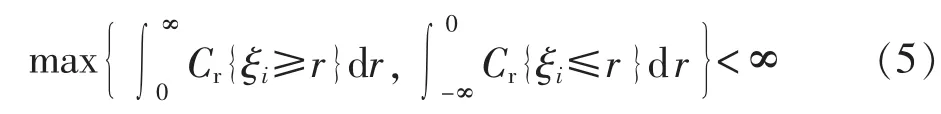
则称模糊变量ξi的期望值是有限的。
参考文献[14],设 ξ 是三角模糊变量(-1,2,3),计算 ξ的期望 E[ξ]。
对于任意的 0≤r<2,有:
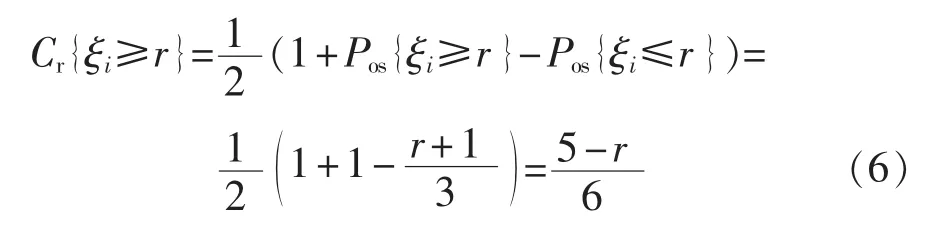
对于任意的 2≤r<3,有:

对于任意的-1≤r<0,有:

由模糊变量ξ的期望值定义可得:

由以上的计算过程可得,对于一般的三角模糊变量、梯形模糊变量的期望值,有如下的结论:
a.若 ξ是三角模糊变量(r1,r2,r3),则 ξ的期望值是;
b.若 ξ是梯形模糊变量(r1,r2,r3,r4),则 ξ的期望值是。
引理1[15]若 ξ、η 是定义在可能性空间(Γ,P(Γ),Pos)上期望值有限且相互独立的模糊变量,则对于任意的实数 a和 b,有 E[aξ+bη]=aE[ξ]+bE[η]。
可信性理论的相关内容可以参阅文献[12,16]。
2 基于可信性理论的电压稳定概率评估
2.1 灵敏度分析法
电力系统静态电压稳定分析方法有很多,其中灵敏度分析法物理概念明确,计算简单,易于实现,在潮流计算的基础上,只需少量的额外计算,便能得到所需的指标,在电压稳定分析研究中得到了广泛的应用[17]。
线性化静态系统功率-电压方程可以表示为:

其中,ΔP为有功注入增量;ΔQ为无功注入增量;JPθ、JPU、JQθ、JQU为极坐标下雅可比矩阵J的分块矩阵;Δθ为电压相角增量;ΔU为电压幅值增量。
一般而言,系统的有功和无功变化都会影响系统的电压稳定性,而因为支路的电抗远大于支路的电阻,所以母线电压对无功注入Q的变化比对有功注入P的变化更为敏感。为简化计算,在每个运行点上只考虑 Q 和 U 之间的关系[18]。 令式(10)中 ΔP=0,可得:

其中,JR=JQU-JQθJ-Pθ1JPU,称为降阶雅可比矩阵,它反映了母线电压值的变化ΔU与无功注入的变化ΔQ间的线性关系。
JR矩阵中的第i个对角元素是节点i的U-Q灵敏度[19]。若JR矩阵的对角元素全为正且不是无穷大,则系统是电压稳定的;若JR矩阵的对角元素不全为正,则系统是电压不稳定的。
2.2 静态电压稳定可信性指标
可信性理论在电力系统中已得到初步应用[20]。接入风电场的电力系统,其风速的不确定性影响了静态电压稳定分析结果的准确性。本文针对风速不确定性,将可信性理论应用到大规模风电并网后的的电力系统的静态电压稳定分析中。
根据灵敏度分析方法,应用可信性理论,可建立在可信性意义下各个节点电压的稳定指标:

其中,ξ为风速,f(ξ)为该风速下JR矩阵的对角元素,风速ξ即为本文设定的模糊向量。该静态电压稳定指标表示在可能出现的风速为ξ情况下,JR矩阵的各个对角元素f(ξ)大于0且小于无穷大的可能性为L。L的取值范围为0~1,反映了不确定因素时JR矩阵对角元素的分布情况;L的值越大,表明对应节点的电压稳定性越好;反之表明对应节点的电压稳定性越差。若L=1,表示JR矩阵对角元素一定大于0。若系统中各个节点的L都为1,说明整个系统具有较好的静态电压稳定性。
2.3 基于可信性理论的电压静态稳定分析计算步骤
对于接入风电场的电力系统,设其风速为不确定参数,则JR矩阵的对角元素即可表示为风速的函数。基于可信性理论的静态电压稳定性分析的步骤如图 1 所示[21]。 图中,“∧”表示取小运算;“∨”表示取大运算;σ为连续取样后各个相对时刻的离散风速值;σ(θk)为 θk时刻的风速离散值;ξ为风速连续值;rr为对角元素最大值与最小值之间的一个任意数。

图1 分析步骤流程图Fig.1 Flowchart of analysis steps
3 算例分析
3.1 IEEE 14节点系统
本文采用的第一个算例是对IEEE 14节点系统进行修改,在节点1接入一个等值风电机组,该等值风电机组代表一个30台额定有功功率为2 MW的双馈感应风电机组的风电场(见图2),其中C表示无功补偿设备。根据接入风电场的电力系统运行的实际情况,风速具有极大不确定性,将风速设定为不确定参数,根据风速预测结果,确定其区间数形式。根据经验值,无穷大取999[19]。采用MATLAB和PSAT电力系统分析软件进行静态电压稳定分析。
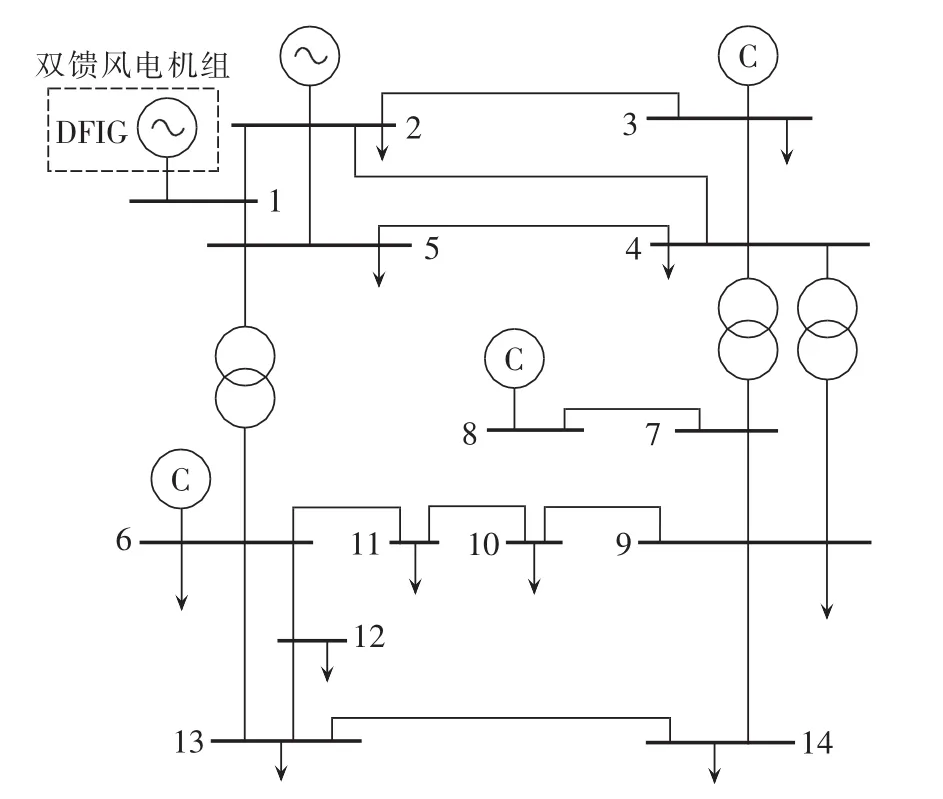
图2 含风电场的IEEE 14节点电力系统Fig.2 IEEE 14-bus power system with wind farm
3.1.1 不同模糊隶属度函数对静态电压稳定分析的影响
分别采用三角隶属度函数和梯形隶属度函数来表征模糊数的分布,并计算在上述2种隶属度函数假设下的对角元素的期望值和均方差,以及各节点的电压稳定指标。
表1给出了采用三角隶属度函数和梯形隶属度函数计算得到的基于可信性理论的JR矩阵对角元素期望值、均方差和各节点电压稳定的可信性指标。由于节点1连接了一台表示风电场的等值风机,而风速的变化使节点1的电压稳定性较其他节点略低些。节点1的电压稳定可信性指标值分别为0.672和0.678,略小于其他节点的电压稳定可信性指标值,这与实际运行是吻合的。从表1中可以看出,采用不同的隶属度函数计算所得的对角元素期望值、均方差和电压稳定可信性指标相差很小,可以忽略。因此,采用不同隶属度函数对计算结果的影响不大。

表1 不同隶属度函数所得JR矩阵对角元素期望值、均方差、电压稳定可信性指标Table 1 Expectation and mean square error of diagonal elements of JRmatrix for different membership function types,and corresponding voltage stability credibility index
3.1.2 抽样次数对结果的影响
为研究抽样次数对计算结果的影响,以三角隶属度函数为例,分别对该算例进行了9次、90次、900次抽样计算。表2—4分别给出了不同抽样次数计算所得的JR矩阵对角元素期望值、均方差及各节点电压稳定可信性指标。

表2 不同抽样次数所得JR矩阵对角元素期望值Table 2 Expectation of diagonal elements of JR matrix for different sampling times

表3 不同抽样次数所得JR矩阵对角元素均方差Table 3 Mean square error of diagonal elements of JR matrix for different sampling times

表4 不同抽样次数所得电压稳定可信性指标Table 4 Voltage stability credibility index for different sampling times
显然,抽样次数越多,均方差越小,即计算结果的精度越高。但也发现,对于该算例,抽样次数达到90次时已经与抽样900次时的计算结果基本相等,所以抽样次数可根据系统规模和计算精度进行选取。
3.1.3 与其他方法计算结果的对比
为验证本文方法的有效性,将本文方法与两点估计法、蒙特卡洛法的结果进行了对比。其中,基于可信性理论方法选用三角隶属度函数表征,抽样90次;两点估计法采用正态分布表征不确定参数风速的分布;蒙特卡洛法进行900次仿真计算。图3—5分别给出了应用本文方法、两点估计法和蒙特卡洛法进行仿真得到的JR矩阵对角元素特征根期望值、均方差及各节点的电压稳定可信性指标的对比结果。

图3 不同方法所得JR矩阵对角元素期望值Fig.3 Expectation of diagonal elements of JRmatrix for different methods

图4 不同方法所得JR矩阵对角元素均方差Fig.4 Mean square error of diagonal elements of JRmatrix for different methods

图5 不同方法所得的电压稳定可信性指标Fig.5 Voltage stability credibility index for different methods
从图3、图4中可以看出,可信性理论法与蒙特卡洛法计算所得的JR矩阵对角元素期望值和均方差都非常接近。一般认为蒙特卡洛法是较接近实际的[22],所以认为可信性理论较两点估计法更接近实际结果。观察图5中3种方法得到的各节点电压稳定可信性指标可知:对于节点1的可信性指标,蒙特卡洛法和可信性理论得到稳定指标分别为0.672和0.658,而两点估计法得到的稳定指标为0.751,与其他2种方法相差较远,结果偏乐观。
蒙特卡洛法需要通过大量反复抽样,对抽样值分别进行仿真计算,工作量大,对于实际电力系统而言不可行,而两点估计法虽然计算量最小,但其不确定参数分布类型的假设对结果的影响较大(见表5)。表5为分别以正态分布和Weibull分布表示风速分布时得到的JR矩阵对角元素期望值、均方差和可信性指标。而在2.1节所述可信性理论中采用不同隶属度函数表征风速时对结果的分布影响较小。因此,可信性理论法较两点估计法能得到更为稳定的计算结果。

表5 不同分布函数所得JR矩阵对角元素期望值、均方差和电压稳定可信性指标Table 5 Expectation and mean square error of diagonal elements of JRmatrix for different distribution function types,and corresponding voltage stability credibility index
3.2 IEEE 30节点系统
本文采用的第二个算例是对IEEE 30节点系统进行修改,在节点3、9、12分别接入双馈等值风电机组、异步风电机组和永磁风电机组。这3个等值风电机组分别代表由30台额定有功功率为2 MW的双馈感应风电机组组成的风电场、30台额定有功功率为1.5 MW的异步风电机组组成的风电场和30台额定有功功率为2 MW的永磁同步发电机组组成的风电场。
表6给出了采用三角隶属度函数和梯形隶属度函数计算得到的基于可信性理论的JR矩阵对角元素期望值、均方差和各节点电压稳定可信性指标。其中,连接了等值风机组的节点3、9、12的电压稳定可信性指标由于风速的不确定性影响较其他节点略低些,这与IEEE 14节点系统的仿真结果相同,与实际运行是吻合的。通过对表1和表6中的各节点电压稳定可信性指标对比,可以看出随着系统规模的扩大和接入风电场容量的增加,整个系统的电压稳定性得到了提高。从表6中可以看出,采用不同的隶属度函数计算所得的对角元素期望值、均方差和电压稳定可信性指标相差很小,所以采用不同隶属度函数对计算结果的影响不大。

表6 不同隶属度函数所得JR矩阵对角元素期望值、均方差、电压稳定可信性指标Table 6 Expectation and mean square error of diagonal elements of JRmatrix for different membership function types,and corresponding voltage stability credibility index
为验证本文提出方法的有效性,同样将IEEE 30节点系统的仿真结果分别与两点估计法、蒙特卡洛法的结果进行对比。其中,基于可信性理论方法选用三角隶属度函数表征,抽样90次;两点估计法采用正态分布表征不确定参数风速的分布;蒙特卡洛法进行900次仿真计算。图6、图7分别给出了应用本文方法、两点估计法和蒙特卡洛法进行仿真得到的JR矩阵对角元素特征根期望值、均方差及各节点电压稳定可信性指标的对比结果。
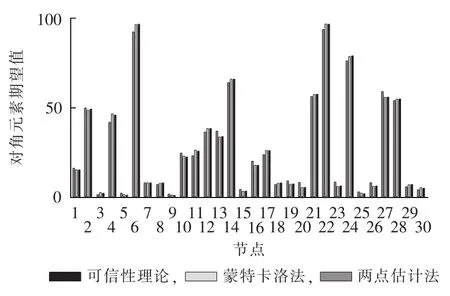
图6 不同方法所得JR矩阵对角元素期望值Fig.6 Expectation of diagonal elements of JRmatrix for different methods

图7 不同方法所得JR矩阵对角元素均方差Fig.7 Mean square error of diagonal elements of JRmatrix for different methods
从图6、7中可以看出,可信性理论法与蒙特卡洛法计算所得的JR矩阵对角元素期望值和均方差都非常接近,而两点估计法计算所得的结果较上述2种方法有较大偏差。这与IEEE 14节点系统的结果相同,所以认为可信性理论较两点估计法更接近实际结果。
4 结论
本文将可信性理论引入含风电场的电力系统静态电压稳定分析中。采用模糊数来表征不确定参数-风速的变化,提出了基于可信性理论的静态电压稳定分析方法,可以得到收缩后的雅可比矩阵对角元素期望值、均方差和各节点电压稳定可信性指标。最后通过与两点估计法和蒙特卡洛仿真法计算结果的对比,说明了本文方法的有效性和优越性。

