考虑调峰特性的电网风电接入能力分析

姜 欣，陈红坤，向铁元，崔若涵，贾体康

（武汉大学 电气工程学院，湖北 武汉 430072）

0 引言

风力发电作为一种较成熟、经济效益较好的清洁能源发电，受到了世界各国的高度重视[1-2]。但由于风电出力具有随机性和间歇性的特点，常规机组的备用容量、调峰能力等调节能力有限，使得评估一个系统的风电接入能力成为了风电并网发电规划的基础。

风电穿透功率极限是评估风电接入能力的一个主要指标，一般定义风电场穿透功率极限为系统能够接受的最大风电场装机容量占系统最大负荷的百分比。风电对系统的影响涉及到许多方面，分析计算十分复杂，因此，至今尚没有统一的求解风电场穿透功率极限的方法。已有的研究中主要有数字仿真方法、频率约束法、数学优化方法3类方法[3]。数字仿真方法，通过PSASP、PSD-BPA等电力系统仿真软件采用试探法，计算风电接入的最大装机容量，该方法是一种验证性的间接计算方法，其不足在于因计算量的限制而无法全面考虑系统的各种运行方式及风况的影响[4-5]；频率约束法则主要适用于分析研究风电场接入较小容量电网的情况[6]；数学优化算法是目前研究最广泛的一种方法，把风电最大装机容量作为优化目标，考虑各类约束条件，进行模型求解，目前已取得了较好的效果。文献[7-8]基于直流近似模型，省略了与节点电压和无功功率有关的约束条件，导致计算存在一定的偏差。文献[9]建立了基于非线性内点法的风电穿透功率极限计算模型，将完整的潮流等式约束考虑其中，但是将风电机组装机容量简单等同于其出力，并不能够很好地处理风电出力的随机性。文献[10]基于相关机会规划理论建立了不确定环境下评估风电场并网容量的优化分析模型，同时考虑了风电的发电能力约束和风电场减出力控制措施的影响，取得了较好的计算结果。文献[11]在风光准入功率极限模型中，考虑了风光的调峰特性和它们之间的互补特点。

已有的研究中考虑风电调峰特性的文献较少，但由于大部分风电具有反调峰特性，会使系统等效负荷峰谷差增大，限制风电接入容量，因此风电调峰特性在穿透功率极限的研究中不容忽视。本文基于机会规划约束建立了风电准入功率极限模型。机会规划约束，约束条件具有一定的置信水平，可以全面考虑多种运行工况的可能性，避免了确定性约束条件下计算结果过于保守，同时弥补了动态仿真仅考虑典型运行模式的不足。此外，本文以湖北某风电场的实际采集数据为例，选取小时作为时间尺度，分析了风速和负荷的分时分布特点，考虑两者在时间上的联系，将风电的反调峰特性引入穿透功率极限模型。采用基于蒙特卡洛模拟的粒子群优化算法求解上述模型，并在IEEE 30节点系统算例中进行了实例计算，计算结果验证了本文所提模型和方法的有效性。

1 风电调峰特性分析

电力系统中的负荷随时间存在峰谷变化，风速的分布特点也与季节、昼夜紧密相关，从而形成了风电场的调峰特性。根据系统运行经验，电力系统日间负荷水平通常高于夜间负荷水平，而大部分风能资源表现出夜间平均风速高于日间平均风速，夜间风电场的出力较大，呈现明显的反调峰特性[16]。

1.1 风电场出力分时分布

风电机组根据桨距特性可分为定桨距和变桨距2种类型[13]。当前的主流机型以变桨距变速机组为主，该机组因其可以实现额定风速以下的最大功率跟踪控制以及额定风速以上恒功率运行而得到广泛应用；定桨距风电机组也因其结构简单、可靠性高，在海上风电机组中应用广泛[14]。不同类型的风电机组的输出特性曲线如图1所示。

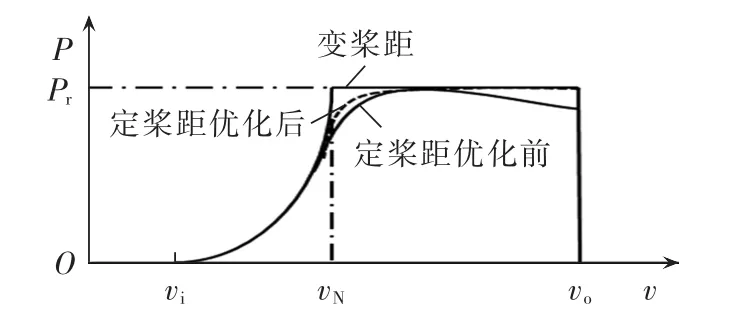
图1 不同类型风电机组输出功率-风速关系曲线Fig.1 Curve of output power vs.wind speed for different types of wind turbine

由图1可以看出，定桨距机组在采用优化控制后，也可接近变桨距风机的功率输出曲线。

假设同一风电场内风速相同，则风电场内同种类型风机的出力相等。本文在忽略风电场尾流和电气损耗的前提下，假设风电场输出功率等于风电场内所有风机出力之和，此时风机的输出主要取决于风机轮毂高处的风速。本文采用如式（1）所示的分段函数简化表达变桨距风电机组的有功出力与风速的关系[15]：

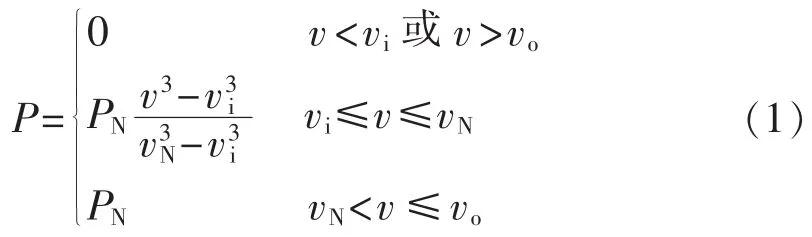
其中，vi、vo、vN分别为风电机组的切入风速、切出风速和额定风速；PN为风电机组的额定功率。

目前已有的研究中，针对风速分布拟合应用最广泛的模型是两参数威布尔分布描述，其概率密度函数为[12]：

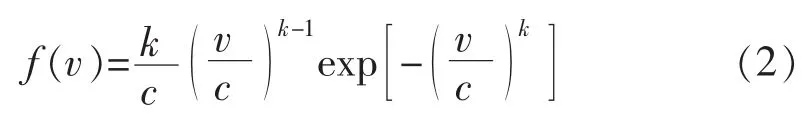
其中，v为实测风速；k为形状系数；c为尺度参数，表示某一段时间内该地区的平均风速。

本文通过对湖北某风电场2011年采集到的风速数据进行整理分析，得出该区域一年四季中冬季风的资源分布，夜间平均风速明显高于白天，表现出较为显著的反调峰特性。因此，考虑最为恶劣的情况，以该区域冬季风资源分布为例，采用极大似然估计的方法，以每小时为时间尺度，将一天的风速数据分为24组，整理出该地区冬季不同时段下的风速威布尔概率分布，见表1。

由尺度参数c可近似表征平均风速大小，从表1可以看出冬季夜间 21∶00—24∶00 和 00∶00—08∶00时段的平均风速整体高于08∶00—21∶00时段的平均风速。

1.2 负荷分时分布

根据系统运行经验和可靠性理论，负荷大小波动服从正态分布[17]。其概率密度函数为：

其中，Pl为节点i的实际负荷大小；μi为节点i的负荷期望值，即预测值；δi为负荷波动的方差。

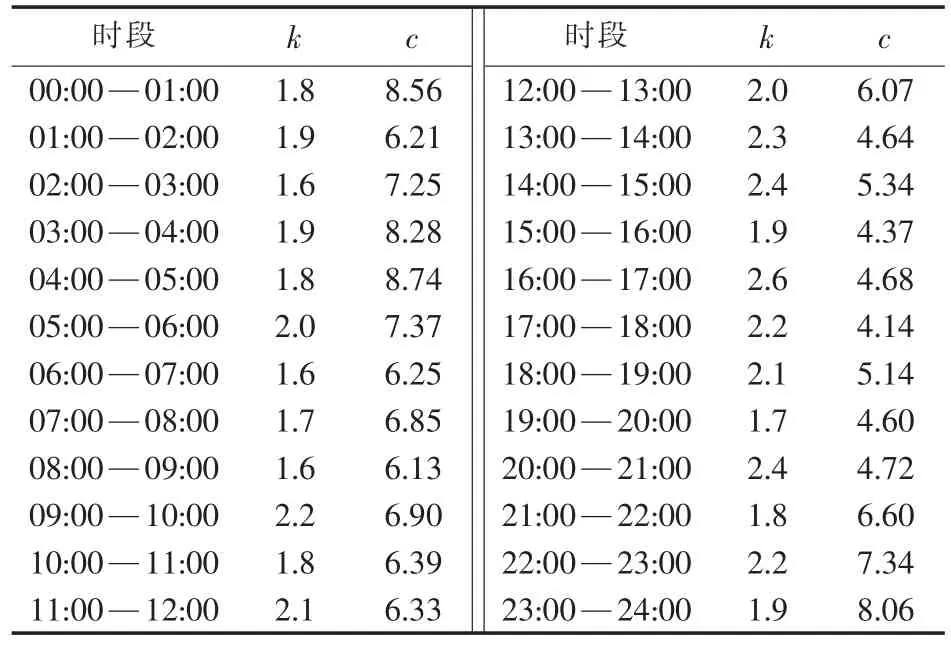
表1 冬季不同时段风速的威布尔分布参数Table 1 Hourly Weibull distribution parameters of wind speed in winter

为考虑负荷以小时为时间尺度变化特点，其均值随时间变化可采用IEEE-RTS[18]可靠性测试系统中的负荷模型。以冬季负荷数据为例，各时段的负荷占峰荷的百分比如图2所示。

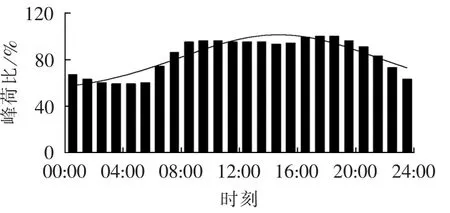
图2 IEEE-RTS负荷模型各时段负荷百分比Fig.2 Hourly load percentage of IEEE-RTS load model

2 最优模型

2.1 机会约束规划原理

机会约束规划是随机规划的重要分支，用于解决在给定置信水平下具有不确定因素的优化问题。如果约束条件中含有随机变量，且必须在观测到随机变量的实现之前做出决策，考虑到所做决策在不利情况发生时可能不满足约束条件，允许所做决策在一定程度上不满足约束条件，但是，该决策应该使约束条件成立的概率不小于某一置信水平[19]。

机会约束规划的一种常见形式如下：

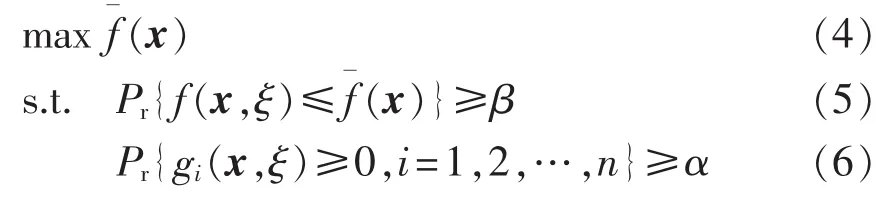
其中，f（x，ξ）为目标函数；gi（x，ξ）为随机约束函数；x为n维决策矢量；ξ为概率密度函数φ（ξ）的随机变量；Pr｛A｝为事件A成立的概率；α和β分别为给定的约束条件和置信水平；为目标函数在概率水平至少为β时的取值。

2.2 基于机会规划约束的风电准入功率极限模型

本文以系统可接纳的最大风电场装机容量作为目标函数，选取常规机组的有功出力和风电场的装机容量作为决策变量进行优化调整，基于机会规划约束建立了如下的风电场穿透功率极限数学模型：

其中，Pw为各节点对应风电场出力；eT为与向量Pw维数相同的列向量，且与风电场节点对应的位置上元素为1，其他位置的元素为0。

由于风电场出力的随机性，如果约束条件仍然是等式，则结果过于保守，而且也不具有实际意义。而具有一定置信水平的机会规划约束弥补了确定性约束仅考虑典型运行模式的不足，涵盖了系统具有多种运行模式的可能性。置信水平的取值来自于系统实际的要求，一般取值在0.9～1.0之间，取值越小，表明引入的风险越大，取值越接近1.0，计算结果越趋于保守[20]。具体约束条件如下：

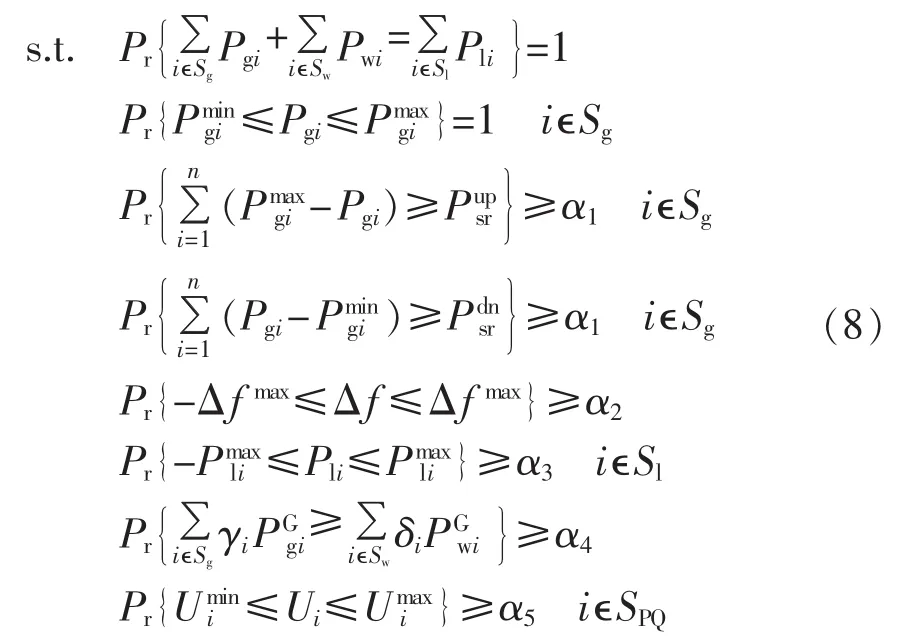
其中，Pwi为风电场的安装容量；Pgi为常规机组的有功出力；Pli为有功负荷；Pmaxgi、Pmingi分别为各发电机组出力的上、下限；Umaxi、Umini分别为各节点电压上、下限；Δf为系统频率差异增量；Δfmax为系统频率偏移限值；Pmaxli为输电线路有功功率限值；Pupsr、Pdnsr分别为系统的旋转备用容量上、下限；γi为常规机组的爬坡能力；PGgi为常规机组的额定容量；δi为风电场以小时为时间尺度的风功率变化系数；PGwi为风电场装机容量；Sg为系统常规发电机组集合；Sw为系统并网风电场集合；Sl为系统负荷节点集合；SPQ为系统节点母线集合；α1—α5为置信水平。

3 基于蒙特卡洛模拟的粒子群优化算法求解

3.1 蒙特卡洛模拟

随机模拟技术为验证概率形式的约束条件提供了有效的途径。本文采用蒙特卡洛模拟，从已知的概率分布中对随机变量进行抽样，从而对系统决策变量进行校验。

针对式（6）中的机会规划约束，对任意给定的决策变量x，先设置N1=0，然后由概率密度函数生成N个随机变量，如果将生成的随机变量ξ和决策变量x代入式（6），满足不等式 gi（x，ξ）≥0（i=1，2，…，n），则N1加1，当N足够大时，根据大数定律，如果式（6）成立，当且仅当 N1/N≥α 时成立。如果 N1/N≥α不成立，则说明通过粒子群优化算法产生的粒子不符合式（6）的概率水平，这样的粒子舍弃，并重新生成新的粒子，直到所有的粒子都满足 N1/N≥α[21]。

3.2 粒子群优化算法

微粒群中的每一个粒子定义为D维空间（待优化问题的解空间，维数为D），粒子以一定的速度Vi＝（Vi1，Vi2，…，ViD）在搜索空间中飞行。 每个粒子具有位置和速度2个特征值，粒子根据自己在解空间中的飞行经验以及群体的飞行经验，动态地调整自己的位置和速度。粒子位置坐标对应的目标函数值即可作为该粒子的适应度，算法通过适应度来衡量粒子的优劣。算法开始时，初始化一组随机解x1、x2、…、xN（N为粒子的个数），然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪2个“极值”来更新自己：一个是粒子本身所找到的最优解，即个体极值pbest；另一个是整个粒子群目前找到的最优解，称之为全局极值gbest。实例计算粒子在找到上述2个极值后，根据下面2个公式来更新自己的速度与位置[20]：

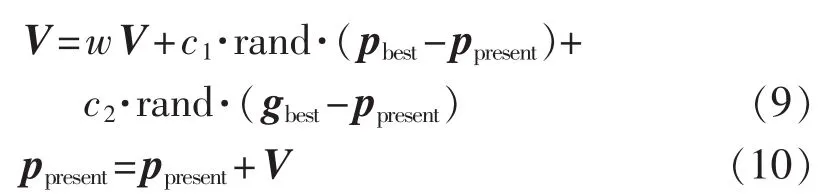
其中，V为粒子的速度；ppresent为粒子的当前位置；rand 为[0，1]之间的随机数；c1和 c2被称作学习因子，通常c1=c2=2；w为加权系数，一般在0.1～0.9之间取值。

已有文献[22-23]通过大量实验证明，如果w随算法迭代的进行而线性减小，将显著改善算法的收敛性能。设wmax为最大加权系数，wmin为最小加权系数，r为当前迭代次数，rmax为算法迭代总次数，则有：

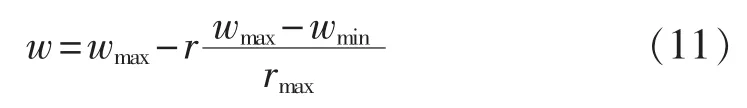
更新过程中，粒子每一维的最大速率限制在Vmax，粒子每一维的坐标也被限制在允许范围之内。同时，pbest与gbest在迭代过程中不断更新，最后输出的gbest就是算法得到的最优解。

3.3 具体求解过程

根据以上的数学模型，采用基于蒙特卡洛模拟的粒子群优化算法流程如下。

a.输入系统信息和风电场信息，调入分时段随机分布参数，设置T=0、N1=0。

b.设置算法参数，在D维问题空间上对微粒群进行初始化，设定群体规模为N，在决策向量x的可行域中产生一随机数并检验该随机数的可行性，重复该过程，从而得到N个初始可行的微粒：xi=（xi1，xi2，…，xiD），其中 i=1，2，…，N，然后再对速度、位置等进行初始化，生成控制变量初始值和粒子初始速度。

c.根据T的数值确定当前时间段，随机生成各风电场风速和负荷，计算出风电出力以及系统潮流；并利用3.1节中介绍的蒙特卡洛随机模拟校验当前系统状态是否满足约束条件（即每个微粒的适应值），若满足则N1=N1+1。

d.对每个微粒，将其适应值与所经历的最好位置的适应值进行比较，检验粒子是否可行，若较好，则将其作为当前最好位置。

e.对每个微粒，将其最好适应值与全局所经历的最好适应值进行比较，检验是否达到最大粒子数，若较好，则将其作为当前的全局最好位置。

f.根据进化方程（9）—（11）进化，更新各粒子速度和位置。

g.对更新后的粒子再次利用蒙特卡洛随机模拟计算 Pr｛gi（x，ξ）≥0，i=1，2，…，n｝并检验粒子的可行性。

h.校验是否达到预设的最大迭代数；若是则认为是一个足够好的适应值。

i.检验此时是否满足T≥24，若不满足则T=T+1，重复步骤c—i；若满足，则输出此时最好的微粒和对应的适应值作为最优解和对应的最优值（即输出风电穿透功率极限值和决策变量最优值）。

4 算例结果与分析

本文以IEEE 30节点测试系统为例，验证上述模型和算法在求解风电穿透功率极限问题上的可行性和有效性。IEEE 30节点测试系统如图3所示，系统总负荷为189.2 MW，系统中常规机组出力上、下限如表2所示（均为标幺值）。假定风电场的平均风速为8 m/s，风电场以功率因数为1.0的恒功率因数方式运行。风电机组的运行参数如下：额定功率为2 MW，额定风速为12 m/s，切入风速为3 m/s，切出风速为25 m/s，各约束条件的置信水平αi如表3所示。

当风电场从不同点接入时，分别计算是否考虑风电调峰特性的风电穿透功率极限，结果见表4。

从表4可看出，未计及风电调峰特性的风电穿透功率极限比计及调峰特性的穿透功率极限高。事实上，由于大部分风电都具有反调峰特性，特别是海上风电场，其反调峰特性比内陆风电场明显得多，不考虑风电调峰特性的穿透功率极限计算结果会过于乐观。同时也可以看出多点接入更有利于缓解线路的传输约束，最大限度地利用风电机组容量。

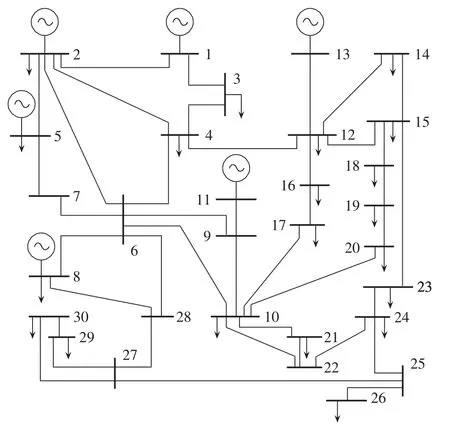
图3 IEEE 30节点测试系统Fig.3 IEEE 30-bus test system

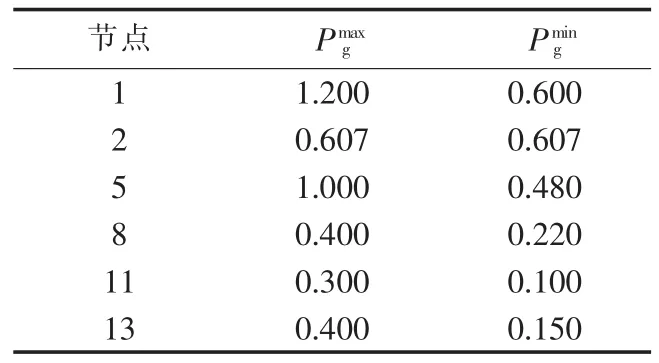
表2 IEEE 30节点系统机组参数Table 2 Unit parameters of IEEE 30-bus system

表3 约束条件的置信水平Table 3 Credit level of constraints

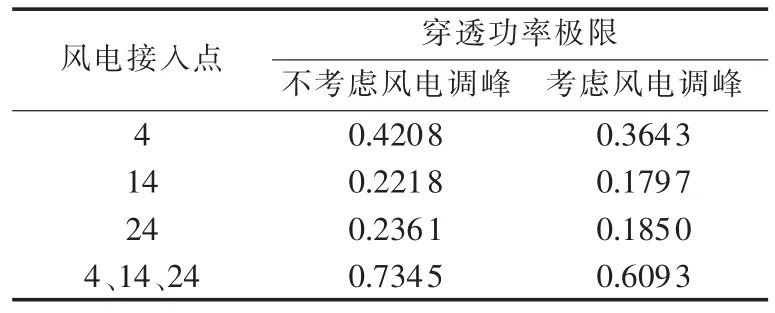
表4 IEEE 30节点系统风电穿透功率极限Table 4 Wind power penetration limit of IEEE 30-bus system

为了研究风电场的平均风速对风电穿透功率极限的影响，在表4考虑风电调峰特性计算条件基础上，研究平均风速对穿透功率的影响，结果见图4。

由图4可以得出，风电场的平均风速增大，对系统的扰动将随之增加，从而限制了风电接入容量，因此风电场规划时，需考虑该地区的平均风速。

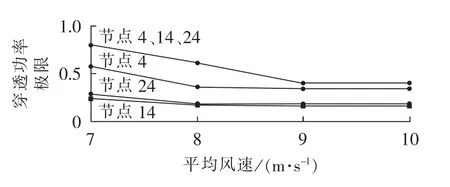
图4 风电场穿透功率极限与平均风速关系图Fig.4 Relationship between wind power penetration limit and average wind speed

不同的风机类型对风电穿透功率也有一定的影响，在表4计算条件的基础上，研究风电机组不同额定容量和不同额定风速对穿透功率极限的影响，以节点24为例，计算结果见图5。

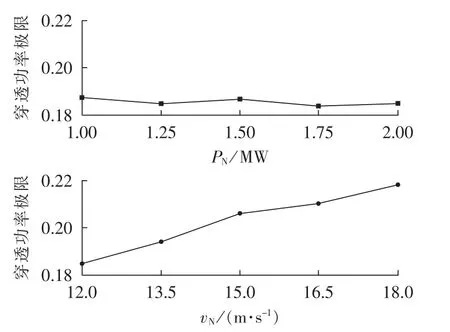
图5 不同参数风电机组的穿透功率极限Fig.5 Wind power penetration limit for different parameters of wind turbine

由图5可以看出，风电机组的额定功率对穿透功率极限影响不大，但是穿透功率极限却随着额定风速的增大而增大。

考虑到定桨距风电机组未采用优化控制方式时其风功率输出曲线（见图1），相比于变桨距风电机组，可表示为PN较小而vN较大的分段函数。因此，仍以节点24为例，对比了PN=2 MW、vN=12 m/s时与PN=1.5 MW、vN=15 m/s时的穿透功率极限，分别为0.1850和0.2068。计算结果表明，仅考虑静态安全稳定约束、功率因数为1.0的运行方式下，定桨距风电机组的穿透功率极限比变桨距风电机组略大。

系统不同的运行工况，对各约束条件的置信水平要求不同。在表4的计算条件基础上，研究约束条件的不同置信水平对穿透功率极限的影响。方案a0为各约束条件置信水平为1.0的情况，方案a1—a5分别为在方案a0的基础上，各约束条件置信水平α1—α5分别取0.98的情况（方案a1为旋转备用约束置信水平α1取0.98，方案a2—a5依此类推），计算结果如图6所示。

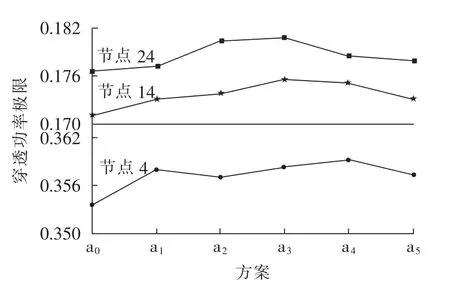
图6 不同置信水平下的风电穿透功率极限Fig.6 Wind power penetration limit for different credit levels

由图6可以看出，约束条件的置信水平不同，风电并网点的穿透功率极限不同，即风电并网点不同，限制其并网容量的主要约束不同。节点24受频率约束和线路传输极限约束的影响较大，而节点4受旋转备用约束和爬坡能力约束的影响较大。因此风电场规划时，需考虑限制并网点的主要约束及实际电网对约束条件置信水平的要求。

5 结论

本文提出了一种考虑风电调峰特性的风电接入能力分析方法，同时考虑风电出力的随机性和风电并网对系统调峰特性的影响，建立了机会约束规划模型，并采用基于蒙特卡洛模拟的粒子群优化算法求解，得出以下结论：

a.在评估风电的接入能力时，忽略风电的调峰特性，会使计算结果偏乐观，为系统的安全稳定运行带来隐患；

b.不同类型的风电机组将在一定程度上影响风电准入功率极限，风电场区域平均风速的大小也会影响风电的接入能力；

c.风电并网点不同，限制其并网容量的主要约束不同。

风电接入后的动态约束和输电线路的故障概率也是影响风电穿透功率极限的关键因素，如何将这些约束考虑进优化模型，是今后研究的重点。