光伏发电系统中超级电容器充电策略
蒋 玮,陈 武,胡仁杰,王晓东,杨永标
(1.东南大学 电气工程学院 江苏省智能电网技术与装备重点实验室,江苏 南京 210096;2.国网山西省电力公司长治供电公司,山西 长治 046011;3.国电南瑞科技股份有限公司,江苏 南京 211106)
0 引言
在可再生能源发电系统,如光伏发电系统和风力发电系统中配以一定容量的储能系统,可以起到平滑功率、提供不间断供电等重要作用[1-3]。超级电容器利用双电层原理直接储存电能,其容量可达数万法拉,是介于蓄电池和传统电容器之间的一种新型储能技术。超级电容器储能技术因为其功率密度高、低温性能好、循环寿命长和对环境无污染等特点得到了广泛的关注和应用[4]。光伏发电系统和超级电容器储能系统配合,可以利用超级电容器的大功率吞吐能力,改善光伏发电系统整体特性[5-7]。
光伏阵列输出功率随光照强度、环境温度以及输出电压不同而变化,但在一定的照度和环境温度下只有一个最大功率点,光伏电池的输出功率和电压随负载变化,最大功率点跟踪(MPPT)控制通过动态改变等效负载以获取最大功率[8-10]。
MPPT控制多通过和光伏电池并联的单级DC/DC变换器实现,但在此种控制方式下,变换器输出直流母线电压会在一个范围内动态变化,如果直接给超级电容器充电,会造成在超级电容器端电压和母线电压差较大时,充电电流过大,在超级电容器等效串联电阻上消耗的功率大,充电效率很低[11-12]。同时,不同的充电方式对超级电容器的充电效率影响较大。本文在分析3种充电方式下光伏电池对超级电容器的充电效率的基础上,选择Boost级联Buck变换器 BoCBB(Boost Cascaded Buck converter)并设计出优化的充电控制策略,在实现光伏电池MPPT控制的同时完成对超级电容器的高效充电,仿真和实验结果验证了所提出的充电控制策略的有效性。
1 超级电容器充电效率研究
1.1 超级电容器改进型RC模型
如图1所示,超级电容器改进型RC模型由理想电容C、串联等效电阻Rs和并联等效电阻Rp组成,由于加入了表征超级电容器漏电流效应的并联等效电阻,相对简单RC电路模型,该模型能较精确地描述电容器的长期工作状态[13-14]。
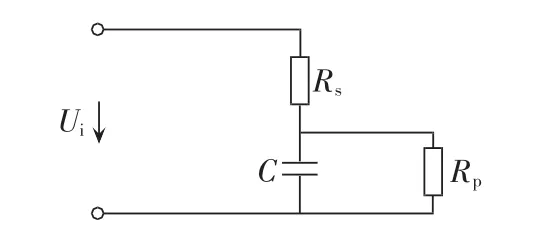
图1 超级电容器的改进RC电路模型Fig.1 Improved RC model of super capacitor
该模型电路属于一阶全响应电路,通过求解一阶全响应解的公式,可以获得初始电压为Ui时超级电容器改进RC电路模型中等效电容电压和输入电流表达式:
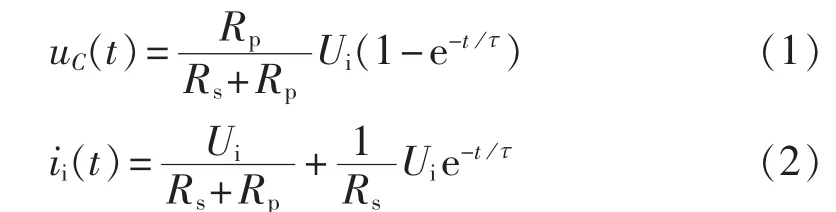
1.2 恒压、恒流、恒功率下的充电效率
超级电容器的充电和蓄电池类似但是又有所不同,因为超级电容器的充放电过程不发生化学反应,所以在充放电过程中受老化影响很小,理论上充放电次数无限。同时,超级电容器本身作为能量缓冲器,对大的脉冲电流吸收效果较好。目前常用的超级电容器充电方式有恒压充电、恒流充电、恒功率充电、脉冲充电等[15]。
利用式(1)、(2),可计算出改进 RC 模型中电容C所存储的电能WC和整个等效模型所吸收的电能Wi,从而可以获得恒压充电方式下的充电效率ηcv和恒流充电方式下的充电效率ηcc:
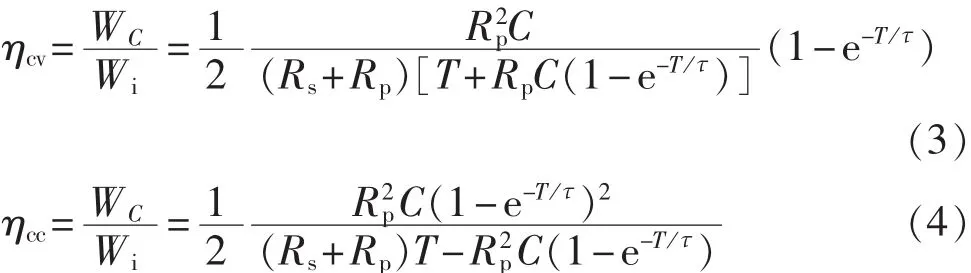
在恒功率充电方式下,超级电容器端电压的微分方程是一个一阶非线性微分方程,较难求解,可通过改进RC电路模型中电容C的端电压和输入电流之间的关系:

使用分段线性逼近的方法,计算恒功率充电方式下的充电效率ηcp。
由此可以获得恒压、恒流和恒功率充电方式下充电效率曲线,分别如图2—4所示。通过对效率曲线的分析可以看出,超级电容器的恒压充电方式实现容易,但充电效率低,最多只有50%;恒流充电方式下,充电速度快,随着时间的延长,充电效率逐渐提高,最终充电效率可超过90%,但充电电路功率随超级电容器电压上升而增大,对充电电路功率要求高;恒功率充电方式下,充电效率随超级电容器电压上升而提高,最终略高于恒流充电,但充电开始时由于端电压低导致充电电流大,对充电电路的电流应力要求较高。
对于超级电容器恒压、恒流、恒功率充电方式的比较可以看出,不同的充电方式各具优点和缺点,在不同的阶段应使用不同的充电方式。
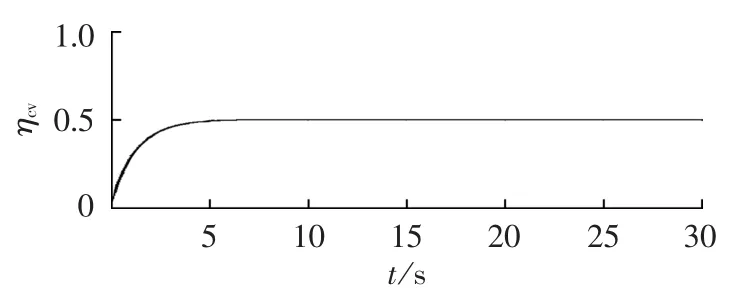
图2 恒压充电效率曲线Fig.2 Efficiency curve of constant voltage charging

图3 恒流充电效率曲线Fig.3 Efficiency curve of constant current charging
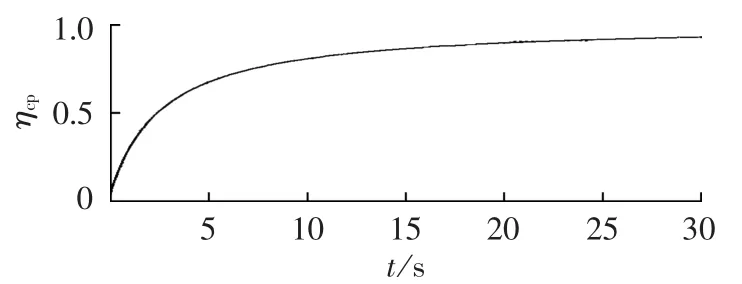
图4 恒功率充电效率曲线Fig.4 Efficiency curve of constant power charging
2 充电系统结构和控制策略
2.1 充电系统结构
工作在MPPT状态下的单级DC/DC变换器只能使光伏发电系统产生最大功率,而无法对变换器输出电压进行控制,也就无法根据不同的充电阶段对超级电容器采用不同的充电方式。而采用变换器级联的方式,可以通过对前后级变换器使用不同的控制策略,达到不同的控制目标[16]。基于此思路,本文提出了基于BoCBB的光伏发电系统对超级电容器储能系统的充电电路,如图5所示。

图5 光伏电池对超级电容器的充电系统结构Fig.5 Structure of charging system of photovoltaic cell to super capacitor
图中,Rpv为光伏电池等效输入电阻,Lg、VT1、VD1、Cbus构成前级 Boost变换器,Cbus、VT2、VD2、Lo构成后级Buck变换器,Rs、Rp和 Cs为使用改进RC模型描述的超级电容器,前后级变换器共用直流母线电压为Ubus。Boost变换器使用MPPT控制策略进行控制,Buck变换器对超级电容器进行充电控制。
2.2 MPPT控制
如图6所示,光伏电池输出功率随端电压的变化呈单峰特性,峰值即为最大功率点。充电系统中的MPPT控制使用改进型扰动观察法,其原理是根据光伏电池输出功率变化方向增加或减小Boost变换器中VT1的占空比dg,增减的步长随光伏电池输出功率和端口电压微分量的比值dP/dU的大小动态变化。在图6中,在离最大功率点较远的A、B点,dP/dU较大,则步长较大,可实现快速跟踪;在C点的时候dP/dU较小,步长减小。越靠近最大功率点步长越小,最后实现在其两边以很小的幅度振荡。
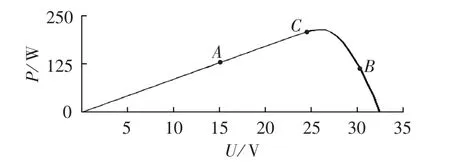
图6 光伏电池功率-电压特性曲线Fig.6 Power-voltage characteristic curve of photovoltaic cell
2.3 超级电容器充电控制策略
在充电开始时,因为超级电容器端电压很低,而其等效串联电阻Rs较小,当很大的充电功率加在超级电容器上,会导致瞬间充电电流极大,如果超过其最大充电电流Iscmax,则可能导致超级电容器的损坏,因此在充电初期,需要将后级Buck变换器输出电压限制在Uo<IscmaxRs,根据Buck变换器的电压变比,需要将VT2占空比限制在:

由于VT2的占空比do存在最小值domin,仅依靠占空比的调节无法在充电初期限制充电电流。在启动时间短、输出功率不大时,可使用限流电阻的能耗型软启动方式,对变换器的效率影响不大[17],因此在充电最初阶段,使用软启动充电方式,通过串联限流电阻Rlim对超级电容器进行充电,Rlim应满足:
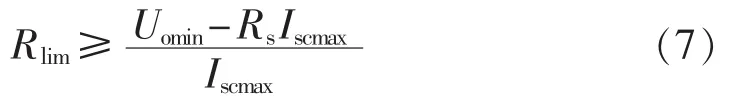
其中,Uomin=dominUbus,当超级电容器端电压uC达到Uomin后,将限流电阻短路。
软启动阶段结束后,进入恒流充电阶段,充电控制系统检测光伏电池输出的电压upv和电流ipv,从而计算出输出功率Pgmax。随着超级电容器端电压uC的上升,其能够承受的最大充电功率Pscmax=uCIscmax也在不断提高,但恒流充电阶段,由于Pscmax<Pgmax时,超级电容器不能在最大充电电流范围内吸收所有由光伏电池产生的功率,此时需要通过控制Buck变换器将充电电流限制在Iscmax。
随着超级电容器电压继续升高,当Pscmax≥Pgmax后,超级电容器能够在最大充电电流范围内吸收由光伏电池产生的全部功率,充电过程进入恒功率充电阶段,充电系统采集超级电容器充电电流isc和端电压uC,计算出的超级电容器当前充电功率和光伏电池在最大功率控制下产生的功率Pgmax及损耗功率Ploss之差ΔP,乘以比例系数K1,作为Buck变换器输出电感电流isc的参考值iref,通过PI控制器产生占空比控制信号do控制VT2以控制充电电流。
3 BoCBB建模与控制器设计
3.1 BoCBB的建模
在恒流充电阶段和恒功率充电阶段,Buck变换器的控制对象都是输出电流。建立BoCBB的数学模型是控制系统设计的依据。BoCBB中的Boost和Buck变换器共用一个直流母线电容,2个开关管使用不同算法分别控制,不存在互补的关系。但是如果将BoCBB作为一个整体建模,在一个变换器模型中包含2个完全独立占空比,将会使该数学模型结构复杂,因此考虑将前后级变换器进行解耦后建模。
图7所示的是BoCBB对超级电容器充电电路的等效电路图,对前级输出电流id和后级输入电流is进行平均化后,可以得到直流母线电容Cd在一个开关周期内的平均电流和电压:
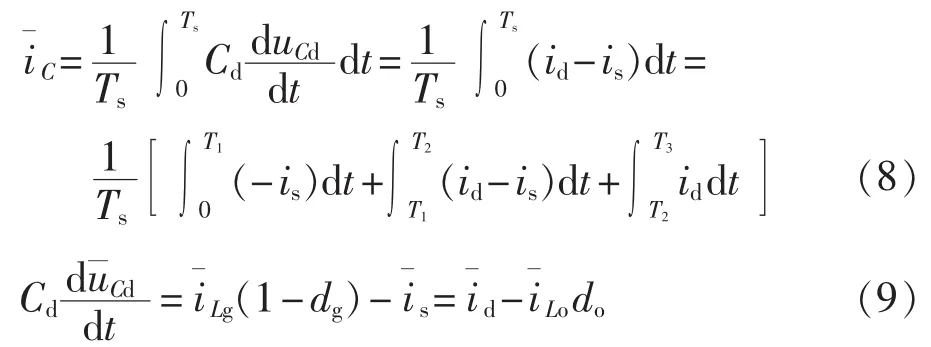
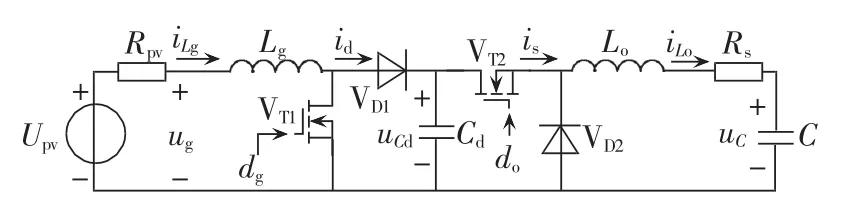
图7 BoCBB等效电路Fig.7 Equivalent circuit of BoCBB
由图8(b)可得Buck变换器+恒流源的状态空间平均方程为:


图8 BoCBB解耦等效电路图Fig.8 Decoupled equivalent circuit of BoCBB
对状态变量和占空比加入小信号扰动:
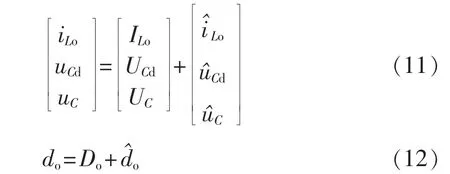
将式(11)和式(12)代入式(10),可以得到变换器的交流小信号状态方程:

通过对式(10)进行拉普拉斯变换,可以得到如下传递函数:
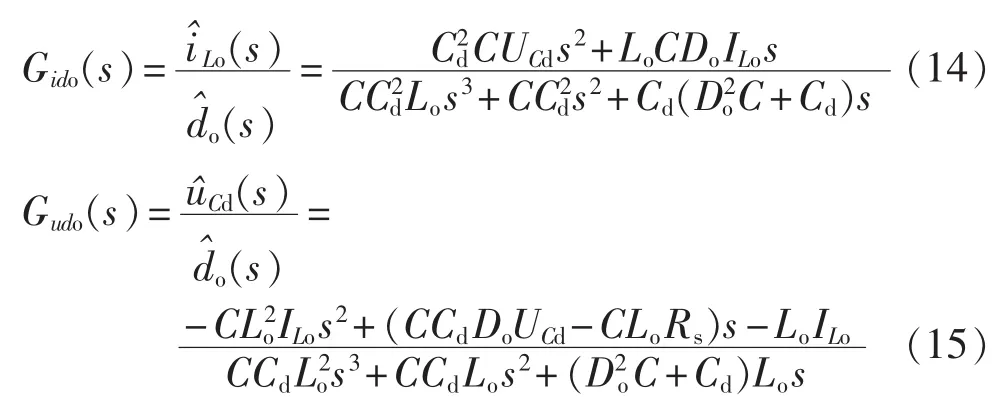
3.2 电流控制器设计
扰动作用下的恒功率控制器电流环如图9所示,其中 Gido(s)为式(14)中的占空比对电感电流的传递函数,Gc1(s)是要设计的电流补偿控制器,N(s)为外部扰动。

图9 扰动作用下的电感电流环Fig.9 Inductive current loop with perturbance
Buck级仿真参数如下:直流母线电容量Cd=2000 μF,超级电容器模组容量Cs=55 F,输出滤波电感量Lo=0.02 H,Buck变换器占空比do=0.5,直流母线电容稳态电压UCd=300 V,输出滤波电感稳态电流ILo=20 A,开关频率fs=20 kHz。将仿真参数代入式(14),可以得到占空比-输出电流传递函数:
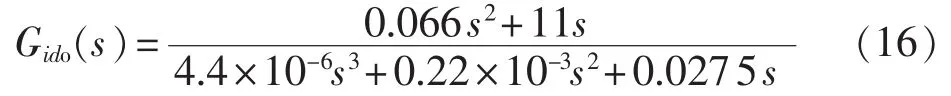
占空比-输出电流传递函数波特图如图10(a)所示。从图中可以看出,开环传递函数频率特性的相移小于-180°,因此对于电流内环,理论上对于任何开环增益,幅值裕度均大于零,系统为无条件稳定的。但在低频段幅频特性为一常数,系统存在稳态误差,可以求得电流环开环直流增益ADC=399.94,系统稳态误差为1/(1+ADC)=0.25%。为了消除稳态误差,同时考虑对系统噪声以及参数变化的抑制,选择电流补偿器 Gc1(s)为 PI环节,其传递函数为 Gc1(s)=),通过在低频段增加1个极点,以改善系统的稳态误差。加入PI环节后,电流环开环传递函数变为:
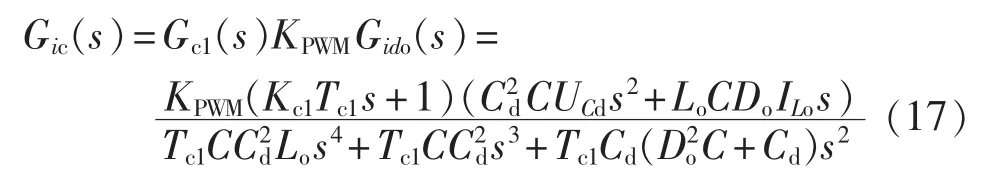
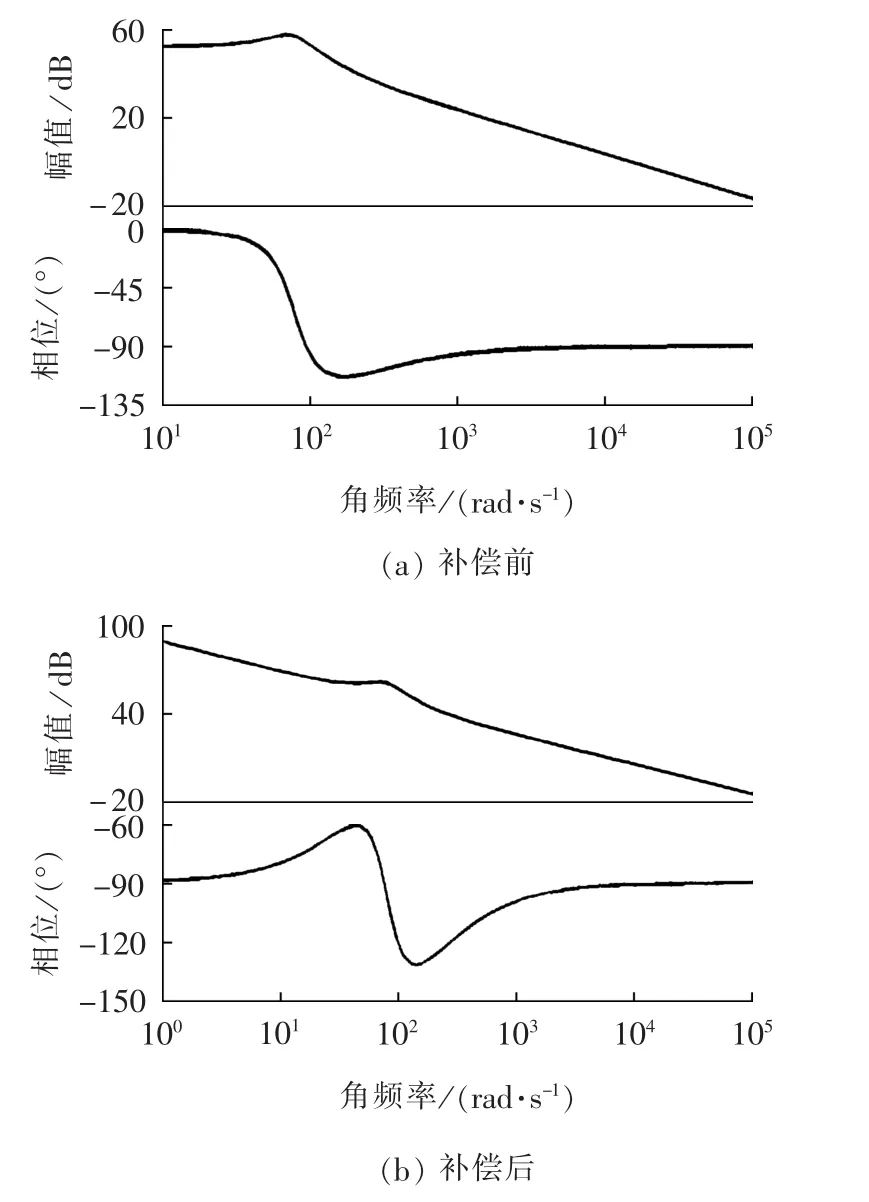
图10 控制环节的波特图Fig.10 Bode diagrams of control loop
取比例系数Kc1=1.35、积分系数Tc1=0.02,电流环开环传递函数如式(18)所示:

加入PI环节后的占空比-电流波特图如图10(b)所示,从图中可以看出,低频段以-20 dB/(°)下降,直流增益无限大,系统消除了稳态误差,穿越频率为3.3 kHz,是开关频率fs的 1/6左右,开环传递函数频率特性的相移仍然小于-180°。
4 充电策略验证
4.1 仿真验证
在MATLAB/Simulink中构建了光伏电池对超级电容器充电系统仿真模型,使用BoCBB,前一级Boost变换器使用MPPT控制器控制跟踪最大功率点,后一级Buck控制器控制对超级电容器的充电。仿真参数如下:光伏电池环境温度T=20℃,光照强度S=180 W/m2,输入电感量Lg=0.01 H,输出电感量Lo=0.02 H,直流母线电容量 Cd=4000 μF,超级电容器等效串联电阻Rs=60 mΩ,超级电容器电容量Cs=1 F,开关频率 fs=20 kHz。
MPPT充电控制器使用之前描述的控制器设计方法设计了电流环补偿环节,PI控制器的比例系数Kc1为4,积分系数Tc1为0.02,设定充电功率为MPPT控制器追踪到的最大功率点功率的90%。设开关管的最小占空比domin=0.03,最大充电电流Iscmax=30 A,Buck变换器输入电压Ubus=150 V,输出最小电压为Uomin>4.6 V,取 Uomin=5 V,由式(7)可得限流电阻Rlim>0.1067 Ω,取 Rlim=0.3 Ω。 首先在恒定光照强度180 W/m2下对MPPT控制器进行了2 s的仿真,超级电容器端电压、充电电流和充电功率波形如图11(a)所示,可以看出在超级电容器端电压达到UC=10 V之前,处于软启动和恒流充电阶段,在限流电阻和恒流控制的共同作用下,实际上超级电容器是以Iscmax=30 A恒流充电,软启动阶段的限流电阻起到了在超级电容器端电压很低的情况下限制充电电流的作用;在超级电容器端电压达到UC=10 V之后,开始恒功率充电,最终充电功率稳定在315 W,为光伏电池输出最大功率的90%。图11(b)所示的是这一过程中的充电效率,充电效率在充电初期较低,最终随着超级电容器电压的升高,充电效率稳定在90%以上。
在 0 s、2 s、4 s 分别设定光照强度为 150 W/m2、200W /m2、300W/m2,获得的光伏电池输出功率 Pmpp和超级电容器充电功率Psc如图12所示,可以看出,使用本文提出的充电策略对超级电容器进行充电,超级电容器的充电功率可以快速跟踪光伏电池输出的最大功率,从而大幅提高充电效率。
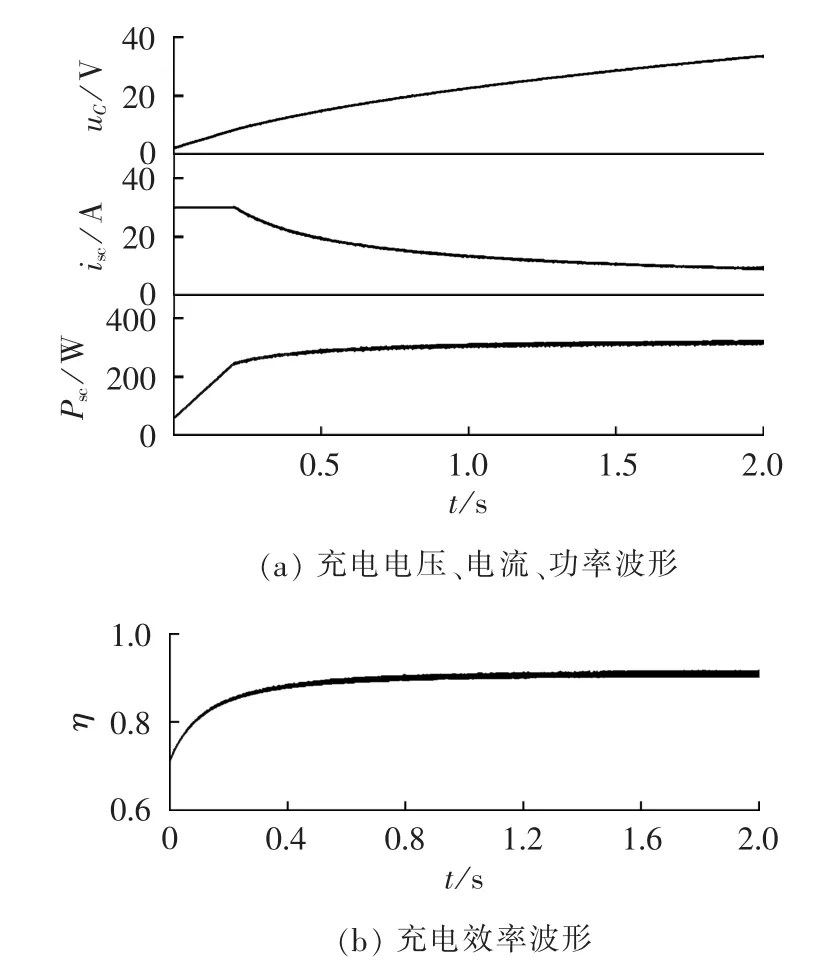
图11 超级电容器充电波形Fig.11 Charging waveforms of super capacitor
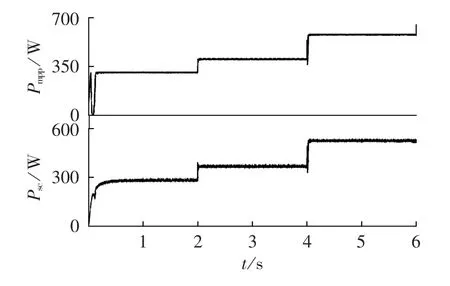
图12 光照强度变化时光伏电池输出最大功率和超级电容器充电功率Fig.12 Maximum photovoltaic cell output power and super capacitor charging power under varying illumination intensity
4.2 实验验证
搭建了实验平台对额定电压UCN为20 V、容量为2F的超级电容器组进行了充电实验。实验分为2组:第1组控制光伏组件输出最大功率为Pgmax1=17W,超级电容器模组的最大充电电流设为Iscmax1=1.5 A;第2组控制光伏组件输出最大功率为Pgmax2=30 W,超级电容器模组的最大充电电流设为Iscmax2=2 A。设Buck部分输出最小电压Uomin=5 V,超级电容器内阻为 0.6,由式(7)得到限流电阻 Rlim>2.733 Ω,实际实验过程中取Rlim=4 Ω。
第1组实验波形如图13所示。充电开始时超级电容器模组端电压为2.486 V,充电结束时为20 V;总充电时间为36.32 s,其中恒流充电14.11 s,恒功率充电22.21 s;总充电效率为74.03%。如果使用光伏输出功率所允许的最大充电电流进行恒流充电,即 isc=Pgmax/UCN=17 /20=0.85 (A),则充电时间需要41.21 s,充电效率为56.21%,由此可见,采用最大功率转移充电方式可以有效提高光伏电池对超级电容器的充电效率并缩短充电时间。

图13 第1组实验波形Fig.13 Waveforms of experiment group 1
第2组实验波形如图14所示。在超级电容端电压uC<5 V时,使用限流电阻进行充电;在5 V≤uC<12.5 V时,使用最大充电电流2 A恒流向超级电容器进行充电;在uC≥12.5 V后,使用恒功率方式充电,充电功率为30 W。充电开始时超级电容器模组端电压为0.86 V,充电结束时为20 V。由于充电功率和充电电流的提高,总充电时间缩短到了20.79 s,其中恒流充电11.84 s,恒功率充电8.95 s,总充电效率下降为64.01%。这是恒流充电时间占整体充电时间增加、恒功率充电时间减少导致的。因此,在光伏电池产生功率增加的情况下,超级电容器模组的最大充电电流也应增加,以减少恒流充电时间,这就需要提高均压电路的分流能力。
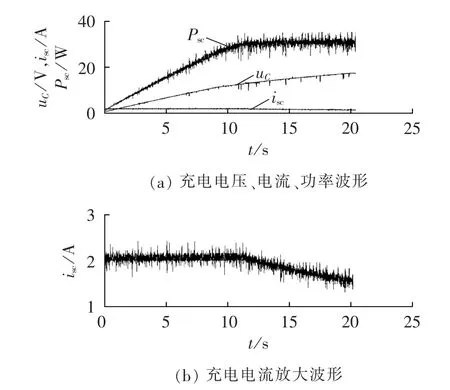
图14 第2组实验波形Fig.14 Waveforms of experiment group 2
5 结论
本文在超级电容器改进RC模型基础上,采用数值方法计算并比较了不同模式下超级电容器充电的效率。结果显示恒流充电和恒功率充电方式在充电效率上优于恒压充电方式,而当使用光伏发电系统对超级电容器储能系统进行充电时,恒功率充电方式较之恒流充电方式更合适。提出了使用BoCBB实现对光伏发电系统的MPPT控制,同时通过在不同阶段控制超级电容器的充电方式从而提高充电效率,并使用等效电流源法对BoCBB进行了建模,在小信号模型的基础上设计了电流环控制器。着重分析了充电开始时的限流问题。仿真和样机实验表明本文提出的充电策略能够有效地提高光伏电池对超级电容器的充电效率,具有实用意义。

