他励直流电动机精确线性化自适应控制

史晓阳

(海军装备部西安局 陕西 兴平 713107)

他励直流电动机精确线性化自适应控制

史晓阳

(海军装备部西安局 陕西 兴平 713107)

基于他励直流电动机数学模型，研究了输出函数对于非线性控制器设计的影响。通过选择不同输出函数，应用精确线性化理论和极点配置方法，设计了转速状态反馈线性化控制器和输入输出反馈线性化控制器。理论推导发现，输入输出线性化控制器是全局稳定的，而状态反馈线性化控制器由于存在奇点，而不是全局能控的。将两种控制器的控制效果进行仿真对比，结果表明，输入输出反馈线性化控制器与状态反馈线性化控制器相比，控制器结构简单、动态性能好、运行稳定。在输入输出反馈线性化控制器的基础上，设计了输入输出反馈线性化控制器的自适应控制器。仿真结果表明，自适应控制器的抗系统参数变化干扰能力相比于输入输出反馈线性化控制器有明显提高。

状态反馈；输入输出反馈；李亚普诺夫函数；奇点

近年来，非线性控制理论的迅速发展使得其在系统建模和系统控制中的应用成为可能。其中，反馈线性化的方法引起了学者的广泛关注，它的核心思想是把一个非线性系统代数的转化为一个（全部或者部分）线性系统，以便可以应用线性系统成熟的设计方法[1-2]对非线性系统进行设计。这种方法已经广泛的应用到了开关变换器控制[3]，电动机控制[4-5]，水利系统[6]等领域。目前，反馈线性化在控制领域的研究，大多是采用状态反馈线性化的方法以实现非线性系统的完全线性化。但是状态反馈线性化需要满足严格的能控性条件和对合条件，而且存在控制器结构复杂，不利于工程实现等缺点。从实用角度来看，实现非线性系统完全精确线性化并不比部分精确线性化更为理想[7]。

本文基于他励直流电动机非线性模型，通过选择不同的输出函数，设计了状态反馈线性化转速控制器和输入输出反馈线性化转速控制器。通过理论推导和系统仿真，比较了两者的控制器结构，稳定运行区域，动态性能。结果表明，输入输出反馈线性化控制器相比于状态反馈控制器具有更好的控制性能，且控制器结构简单，更具有实用价值。在电动机运行过程中，电动机的负载、励磁电阻和电枢电阻会发生变化，这将严重影响控制器的控制性能，为了提高控制器抗参数变化干扰的能力，在输入输出反馈线性化控制器的基础上，设计了输入输出反馈线性化的自适应转速控制器。

1 他励直流电动机非线性模型

电动机控制的目标是控制电动机转速按照期望的指标运行。对于他励直流电动机非线性系统，选取电机转动角速度，电枢电流，励磁电流作为状态变量，即x=(ω iair)T。选励磁电压ur为控制量，即u=ur，系统状态方程[8]可写为

设电动机稳态转速x1m=wm时，解方程组

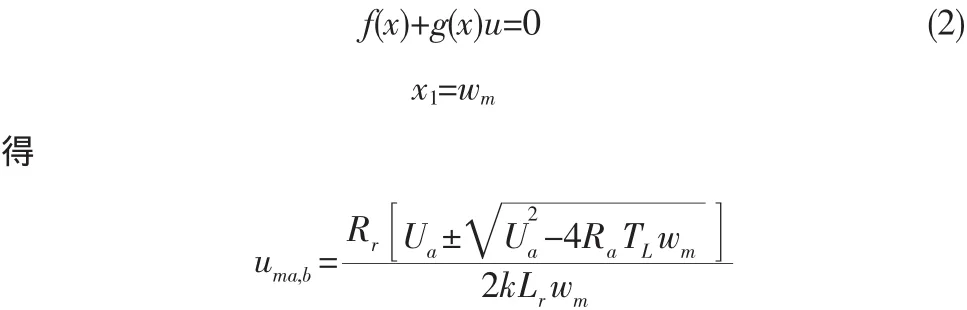
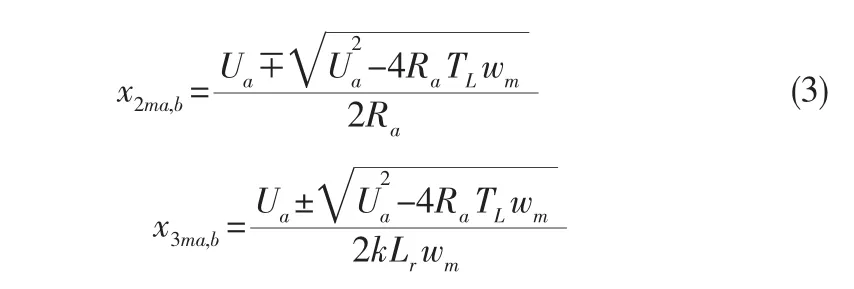
由计算结果可知，对于给定的稳态转速wm，有两组稳态励磁电压、电枢电流、励磁电流。容易看出，b组数据对应的稳态平衡点是物理上无法实现的，a组数据对应的平衡点是我们期望的电动机运行平衡点。所以当系统控制达到稳态转速wm时，期望的稳态电枢电流为x2ma，稳态励磁电流为x3ma。

2 精确线性化极点配置控制器设计

2.1 状态反馈线性化控制器设计

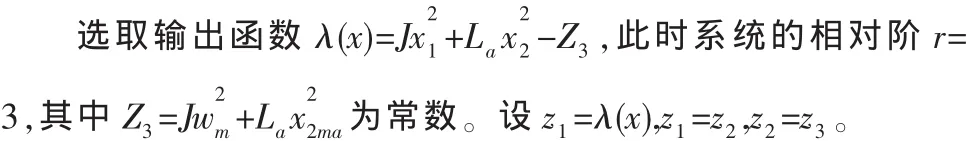
则在此坐标下得到状态反馈线性化控制输入为：

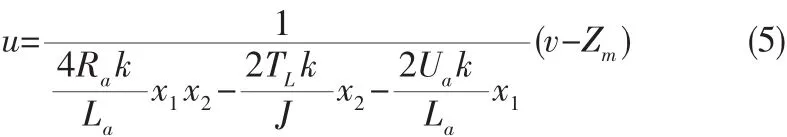
其中，v为线性化虚拟输入，Zm为z˙3中不包含控制信号 u的项。经坐标变化和状态反馈变换后，原非线性系统转化为线性化系统。

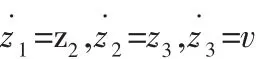
显然，线性化后的系统是能控的线性系统，应用线性系统极点配置法设计闭环，即 v=-k1z1-kz2-k3z3（其 k1,k2,k3＞0 中）。则加入闭环控制的控制规律为

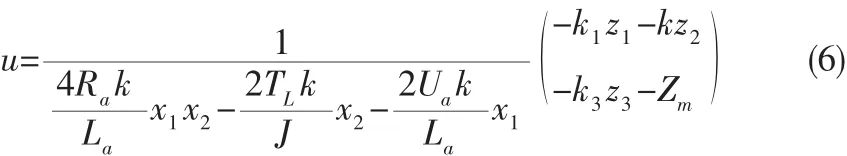
2.2 输出反馈线性化控制器设计

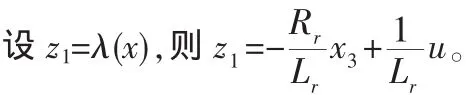
在此坐标下得输出反馈线性化

应用极点配置法设计非线性控制器的闭环，即v=-kz1（k＞0）。

2.3 仿真实验

为了比较两种控制器的控制效果，本文使用Matlab中的Simulink对所建系统的模型进行仿真。他励直流电动机的负载额定转矩为29.2 N·m，电枢电压为240 V，电枢电阻为0.6 Ω，电枢电感为0.012 H，励磁回路电阻为240 Ω，励磁回路电感为0.12 H，电枢与励磁回路互感为1.8 H，转动惯量为1.0kg·m2，电势常数取经验值k=15，额定转速为100 rad/s。

图1为电动机额定状态下，状态反馈线性化控制器和输出反馈线性化控制器启动和调速的转速响应曲线。为了考察系统的动态性能，在5 s时调节控制规律，使电动机转速从100 rad/s稳定到127 rad/s。

从图中可以看出，基于反馈线性化设计的电动机闭环转速控制器具有很好的动态性能。其中，输出反馈控制器相比于状态反馈控制器具有启动快，调速迅速，超调小等优点。

仿真过程中发现，输入输出反馈线性化控制器的结构比状态反馈线性化控制器简单的多，更利于工程实现。而且，状态反馈控制器由于不是全局能控的，当闭环反馈系数或者电动机初始值取值某些值时，控制器会出现控制失效现象，这就使得控制器闭环设计复杂，运行稳定性降低。综上所述，对于他励直流电动机非线性系统，输入输出反馈线性化控制器相比于状态反馈线性化控制器是更好的选择。

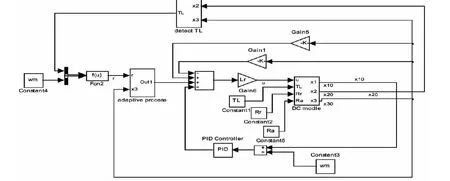
图2 输入输出反馈线性化自适应控制仿真图Fig.2 Simulation block diagram of input-output feedback linearization adaptive control

3 输入输出线性化自适应控制器设计

电动机在运行过程中，电机负载不可能严格稳定在额定负载值，而且随着电动机运行，励磁电阻和电枢电阻会有很大的漂移，这都会严重影响控制器的控制性能。为了提高控制器抗参数不确定性干扰能力，在上述研究的基础上设计了输入输出反馈线性化自适应控制器。

3.1 控制器设计

输入输出反馈线性化自适应控制器是由上述输入输出线性化控制器、负载检测反馈环路和自适应环节构成，如图2所示。

其中，负载检测环路通过在线辨识负载变化，并将实际负载值实时反馈到控制器，在电动机运行过程中不断调节控制器的参数，以达到抑制负载变化的效果。

电机温升是由于电机发热而引起的电机与周围环境的温度差。温升对直流电动机的影响主要体现在励磁绕组和电枢绕组电阻随温度变化的热效应[9]。

选定20℃时的电阻为R0，金属材料的电阻随温度变化的关系可近似表示为

电机的温升与电机运行时间的关系可以近似的表示为

其中，α为电阻温升系数，T为电阻温度，Tn为电机稳态温升，τ为材料的发热时间常数。将 式(10)代入（9）式得绕组电阻随电机运行时间的关系式为

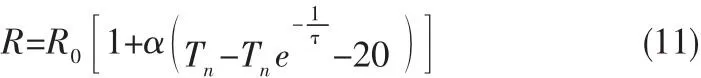
根据中小型旋转电机安全通用要求标准[10]，经计算可知：α=0.003 93（纯铜）Tn=145，τ=80。

自适应环节用于抑制形式如式（11）所示的励磁电阻和电枢电阻随电机运行时间变化对控制器的影响。

3.2 仿真实验

为了考察自适应控制器的抗参数不确定性干扰能力，本文分别为自适应控制器和输入输出反馈线性化控制器加上阶跃变化的负载干扰和电机温升引起的绕组电阻变化干扰，比较两个控制的控制效果。图3为5 s时在电动机转矩控制端加入大小为10 N·m的干扰力矩，系统的转速响应曲线。从图中可以看出，自适应控制器能够迅速的消除负载变化引起的电动机转速波动。

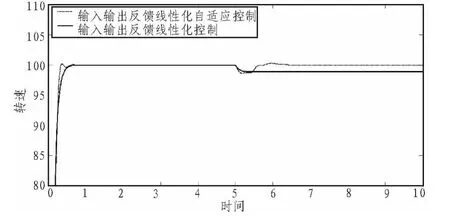
图3 力矩干扰下转速响应曲线Fig.3 Speed response curve with disturbance torque

图4为加入电机温升引起的绕组电阻变化干扰后，系统的转速响应曲线。从图中可以看出，自适应控制器能够很好的抑制绕组电阻变化对系统的干扰，准确迅速地将电动机控制到指定的转速。

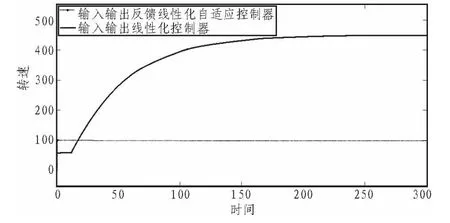
图4 电阻变化干扰下转速响应曲线Fig.4 Speed response curve with resistance variation interference

4 结论

本文基于他励直流电动机数学模型，应用精确线性化理论，设计了输入输出反馈线性化和状态反馈线性化闭环转速控制器。理论推导表明，对于他励直流电动机非线性模型，输出反馈线性化会比状态反馈线性化控制器具有更大的稳定控制区域。仿真过程中发现，由于状态反馈控制器存在奇点，不是全局能控的，极点配置参数、稳态转速的设定和初始状态都会影响控制过程中系统的状态轨迹，从而可能使系统运行到奇点区域，出现控制器失效现象。这就使得控制器闭环设计变得复杂，且大多情况下无法选择最优的闭环控制参数。相比而言，输出反馈线性化控制器具有动态调速性能好；结构简单，易于工程实现；控制器运行稳定；系统闭环设计简单灵活等优点。在输入输出反馈线性化控制的基础上，设计了输入输出反馈线性化自适应控制器，仿真结果表明自适应控制器在电机参数不确定情况下具有很好的控制性能。

[1]程代展.应用非线性控制[M].北京：机械工业出版社，2006.

[2]贺昱曜，闫茂德.非线性控制理论及应用[M].西安：西安电子科技大学出版社，2007.

[3]帅定新，谢运祥，王晓刚，等.Boost变换器非线性电流控制方法[J].中国电机工程学报，2009,29(15)：15-21.

SHUAI Ding-xin,XIE Yun-xiang,WANG Xiao-gang,et al.Nonlinear current control method for boost converter[J].Proceedings of the CSEE,2009,29(15):15-21.

[4]孟昭军，孙昌志，安跃军，等.状态反馈精确线性化永磁同步电动机转速控制[J].中国电机工程学报，2007，11(1)：21-28.

MENG Zhao-jun,SUN Chang-zhi,AN Yue-jun,et al.Speed control of permanentmagnet synchronousmotor based on exact linearization via state variable feedback[J].Proceedings of the CSEE,2007,11(1):21-28.

[5]曹建荣,虞烈,谢友柏.磁悬浮电动机的状态反馈线性化控制[J].中国电动机工程学报，2011,21(9):22-26.

CAO Jian-rong,YU Lie,XIE You-bai.Dynamic feedback linearization control for induction type bearingless motor[J].Proceedings of the CSEE,2011,21(9):22-26.

[6]鲍海燕，杨建东，付亮.基于微分几何的水电站过渡过程非线性控制[J].水利学报，2010，41(11)：1339-1345.

BAO Hai-yan,YANG Jian-dong,FU Liang.Nonlinear control of the transient process in hydropower station based on differential geometry theory [J].Journal of Hydraulic Engineering,2010,41(11):1339-1345.

[7]李啸骢，程时杰，韦化，等.输出函数在单输入单输出非线性控制系统设计中的重要作用[J].中国电动机工程学报，2004，24(10)：50-55.

LI Xiao-cong,CHENG Shi-jie,WEI Hua,et al.Importanl effection of the output function in siso nonlinear control system design[J].Proceedings of the CSEE,2004,24(10):50-55.

[8]李殿璞.非线性控制系统理论基础[M].哈尔滨：哈尔滨工业大学出版社，2006.

[9]陈旭东，冯攀.温升对并励直流电动机性能的影响[J].微特电机，2011,7:25-28.

CHEN Xu-dong,FENG Pan.Influnce of Temperrature rise on shunt DC motor performance[J].Special Electrical Machines,2001,7:25-28.

[10]中华人民共和国国家标准[S].中小型旋转电机安全通用要求，GB14711-93.

Adaptive speed control for separately excited DC motor based on exact linearization method

SHI Xiao-yang
(Xi'an Bureau of Naval Armament Department,Xingping 713107，China)

Based on the mathematical model of separately excited DC motor,the influence of output functions to nonlinear controller is studied.Exact linear theory and the pole assignment method are used to design state feedback linearization speed controller and input-output feedback speed linearization controller by selecting different output functions.The theoretical analysis found that the input-output linearization controller is globally stable.Due to the presence of singular points,state feedback linearization controller is not a global controller.The simulation results show that input-output feedback linearization controller has a more simple structure,better stable operation and dynamic performance compared to state feedback linearization controller.On the basis of input-output linearization controller,the input-output feedback linearization adaptive controller is designed.The simulation results show that the adaptive controller has a stronger anti-interference capability compared to input-output feedback linearization controller.

state feedback；input-output feedback;Lyapunov function;singularity

TN-9

A

1674-6236（2014）13-0175-04

2013-10-13 稿件编号：201310066

史晓阳（1987—），男，河北隆尧人，硕士，助理工程师。研究方向：电力电子与电机拖动。