GPS/SⅠNS超紧组合导航系统自适应混合滤波算法

周卫东，蔡佳楠，孙 龙

(哈尔滨工程大学自动化学院，150001哈尔滨)

GPS/SINS超紧组合导航系统在建模时，将导航参数的误差作为估计状态，称为间接法滤波.间接法滤波有两种，分别是输出校正和反馈校正.理论上，当模型能够准确反映系统本身时，输出校正和反馈校正的估计效果是一致的［1］.工程实践中，输出校正实现简单，滤波器故障不影响SINS工作，但它只能改善输出的准确性，不能对SINS内部误差作修正，长时间工作时，SINS误差累积，最后使系统模型跟实际模型不匹配，导致滤波精度下降或发散;反馈校正估计的是经过校正的导航参数误差，保持为小量，没有模型误差，更接近于真实系统，但是反馈校正实现复杂，滤波器故障或估计精度不高会污染SINS输出，使系统可靠性降低［2］.文献［3］结合这两种结构的优缺点提出了混合校正滤波结构，该结构只有在所有状态估计精度都很高时才能得出较好的滤波结果，而状态的估计精度是由其可观测性决定的［4-5］，因此这种结构只能提高完全可观系统估计精度，对于GPS/SINS超紧组合导航系统这种不完全可观测的系统是不适用的.

对此，文献［6］中给出以奇异值分解(SVD，singular value decomposition)可观测度分析方法为基础的自适应反馈校正滤波方法，它将归一化的奇异值作为反馈因子，对SINS进行反馈校正.该方法根据载体的运动状态实时计算系统的可观测性矩阵，进而获得反馈因子，而随着时间的增长，可观测性矩阵的维数急剧增加，从而导致计算量的增大，甚至会出现维数灾难，导致系统崩溃;同时该方法在计算可观测度的过程中进行了无量纲化处理，这种处理并不能保证处理前后可观测度信息是一致的［7］，因此文献［6］计算出的反馈因子与系统真实情况不完全相符.

针对以上问题，本文在文献［8-10］中提出的超紧组合模型基础上重新推导出线性的量测方程，并给出自适应混合校正滤波方法.该方法引用Ham的特征值和特征向量可观测性分析方法［11］，将滤波过程中计算出的状态误差方差阵进行规范化，求取其特征值，将归一化的最小特征值对应的特征向量作为反馈因子，确定反馈量.这种混合校正方法相对于文献［6］来说，不受误差模型和运动时间的限制，计算量相对较小.

1 GPS/SINS超紧组合导航系统误差模型

状态变量为:位置误差δR=[δLδλδh]T;速度误差δv=[δvEδvNδvU]T;平台失准角φ =[φEφNφU]T;加速度计零位误差▽=[▽x▽y▽z]T;陀螺常值漂移ε=[εxεyεz]T;接收机钟差为 δtu，钟差漂移为 δtru．则系统误差方程为［10，12］

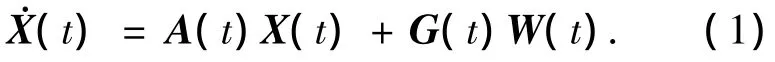
在GPS接收机中，接收到的卫星信号经变频和解调后进入到Ⅰ-Q通道，Ⅰ-Q信号的期望值与载体的速度误差及位置误差满足如下关系式:

这里利用Ⅰ和Q的期望值E［Ⅰ］和E［Q］代替Ⅰ和Q本身对系统进行建模．其中，A为卫星的信号强度;T为时间常数;ω为载波角频率;c为光速;ωe和φe满足如下关系式:

其中:Ru和分别为接收机到地心距离矢量的测量值和估计值;vu和分别为接收机到地心速度矢量的测量值和估计值;Re=|Ru-|和ve=|vu-v|分别代表位置误差和速度误差．

同理，将SINS的测量值与估计值之差代入式(2)～(5)，计算得到SINS对Ⅰ，Q的预测值为

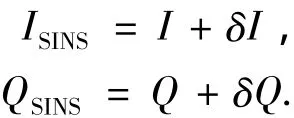
接收机第i个Ⅰ-Q通道输出值为

将 ⅠSINS，QSINS与 ⅠGPS，QGPS之差作为测量

则GPS/SINS超紧组合导航系统如图1所示［13］.δⅠ，δQ为 SINS 对Ⅰ，Q的预测偏差．ηⅠ，ηQ是接收机Ⅰ-Q 通道噪声，ηⅠ～ N(0，1)，ηQ～ N(0，1)，E［ηⅠηQ］=0．

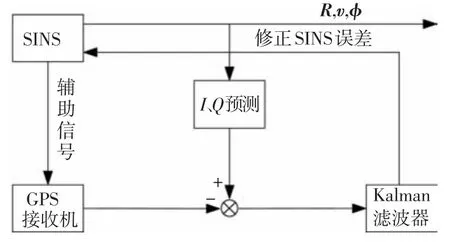
图1 GPS/SⅠNS超紧组合导航系统

在文献［8-10］中选取Re和ve为状态量，则由式(2)和式(3)分别得到

由此推导得到量测方程是关于Re和ve的非线性方程［14］．为此将Re和ve重新定义为

并且

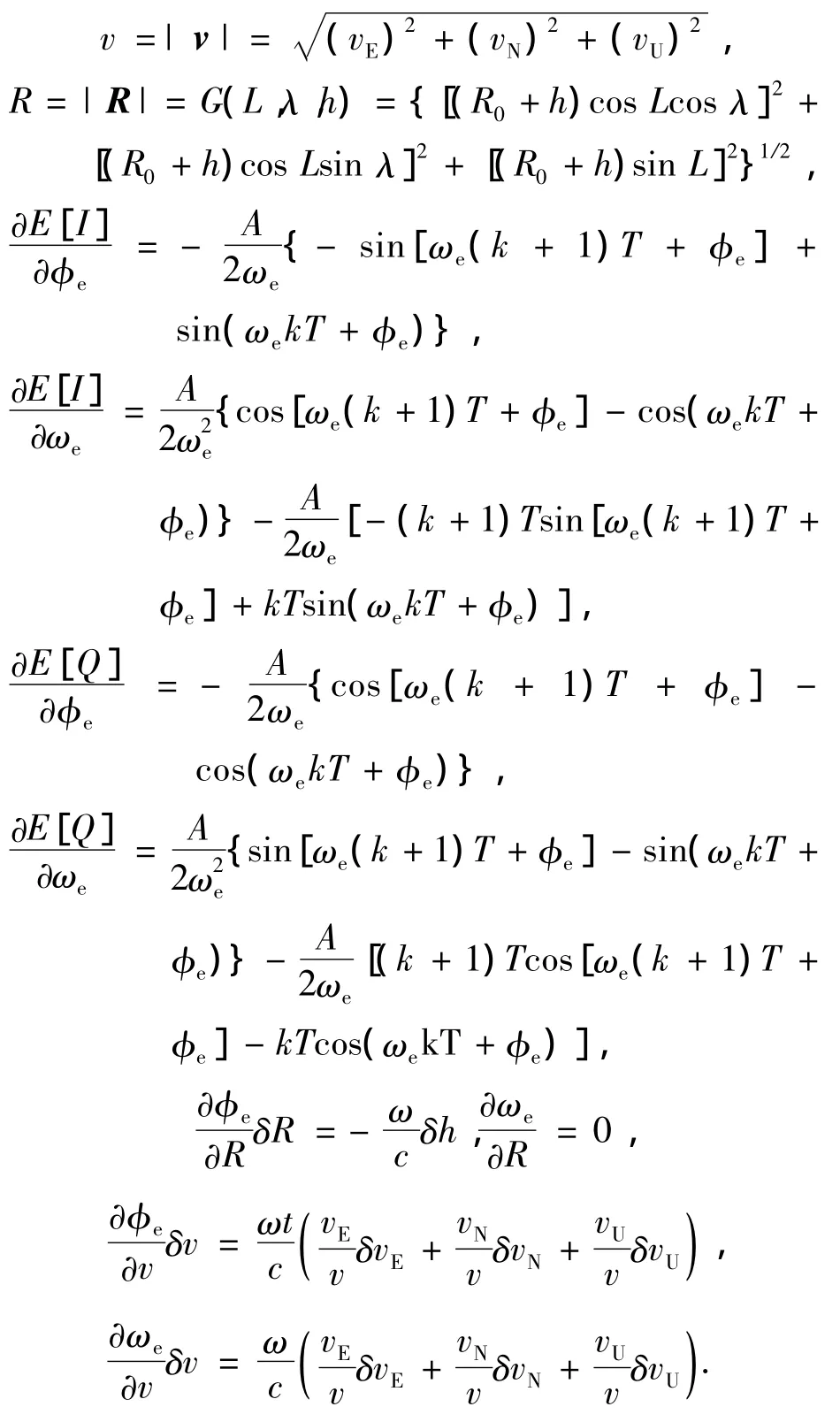
其中:L为纬度;λ为经度;h为高度;R0为地球半径;vE，vN，vU分别为载体在东、北、天方向的速度分量．综上所述，量测方程为［15］

观测矩阵为

其中:

其中i=1，2，…，n为跟踪卫星的数目．

2 特征值特征向量可观测性分析方法

其协方差为

其中P为误差协方差阵，pij为其元素．选取约束条件为

拉格朗日方程满足

其中λ为拉格朗日因子．将式(12)代入式(14)得

则

当且仅当

方程(16)有非零解.因此，式(16)的解为P的特征向量，将式(16)的两边分别左乘vT得

将式(12)，式(13)代入式(18)得

通过全等变换将P规范化为PN+(k)，

其中

全等变换使特征值大小发生变化，被限定在［0，1］之间(n为系统阶数)，但它正特性和矩阵的秩不变．由此可以发现，PN+(k)矩阵的特征值实际上是对应状态的方差.那么，特征值越小，其对应的状态(或状态的线性组合)的可观测性越强［11］.因此，最小的特征值对应可观测性最好的状态(或状态的线性组合).

对动态系统进行可观测性分析时，误差协方差阵的特征值和特征向量法相对于分段定常系统(PWCS，piece-wise constant system)可观测性分析方法和SVD有如下优点:

1)PWCS和SVD分析系统可观测性时，都只是在齐次系统方程的基础上进行的，没有考虑到系统过程噪声和量测噪声的影响;而特征值和特征向量法利用了包含噪声影响的误差协方差阵，分析系统在有噪声情况下的可观测性;

2)SVD在计算可观测度的过程中进行了无量纲化处理，这种处理并不能保证处理前后可观测度信息是一致的［7］;而特征值和特征向量法中采用的全等变换不改变特征值的特性，变换前后得到的可观测性结论一致;

3)PWCS和SVD某一时刻的可观测性矩阵，包含当前时刻之前的所有时间段的可观测性矩阵，可观测性矩阵维数随时间延长而增加，计算量增大;而特征值和特征向量法需要求解每一时刻误差协方差阵的特征值和特征向量，而该协方差阵刚好是系统滤波迭代计算时产生的中间数据，且其维数取决于系统状态的个数，不随时间的延长而增加，计算量相对较小;

4)特征值和特征向量法具有更加明确的物理意义，易于理解.

3 基于可观测性的混合校正滤波器设计

由于状态的估计精度由其可观测性决定，可观测性高的状态其估计精度高，可观测性低的状态其估计精度低，为使反馈量更具有可靠性，将估计的误差量按可观测性的强弱成比例反馈给SINS，修正SINS和GPS原始数据.因此，在反馈校正中反馈因子是一个重要的参数，它的大小应该由系统状态可观测性决定，即可观测性高的状态给予较大的反馈因子，可观测性低的状态给予较小的反馈因子，不可观测的状态反馈因子为零，并且反馈因子能够随着状态可观测性的变化而变化.基于以上分析，利用滤波过程中的误差协方差阵来实时计算反馈因子可以有效满足上述要求.

文献［16］指出小的特征值对应高可观测度，相应的特征向量给出高可观测度的“方向”，即最小特征值对应的特征向量可以指示出各个状态可观测性强弱.将该特征向量的元素做归一化处理，得到的即为状态(或状态的线性组合)的可观测度，它是衡量状态估计精度的数值指标［4，16］.那么，利用可观测度与估计精度呈正相关的关系，选取最小特征值对应的归一化后的特征向量vmin中的元素vi(i∈{1，2，…，n})为相应状态的反馈因子，将反馈因子与状态估计值的乘积作为反馈量．该反馈量虽然比较保守，但其保留了可观测性强的状态对系统良好的修正能力，同时削弱了可观测性弱的状态对系统盲目修正造成的不良影响．混合校正滤波器的结构如图2所示．

图2 混合校正滤波器

将vmin中的元素vi与系统状态对应后，得到的反馈因子为α =diag{ α1α2…αn}，其中 αi∈{v1v2…vn}．当αm=1，m∈{1，2，…，n}，表示第m个状态的可观测性最高，其估计精度最高，完全反馈;αe=0，e∈ {1，2，…，n}，表示第 e个状态的可观测性最低，其估计精度最低，不反馈;0＜αk＜1，k∈{1，2，…，n}，第k个状态的可观测性介于第m和第e个状态之间，反馈量为αkk．

为使该混合校正滤波器发挥最优性能，在估计误差较大的滤波初始阶段只进行输出校正，滤波器稳定后，再进行混合校正.输出校正的周期与滤波器周期相同，反馈校正的周期可调，是滤波周期的整数倍.

4 仿真与分析

仿真条件:初始位置误差为[2m 2m 2m]，初始速度误差为[0.6 m/s 0.6 m/s 0.6 m/s]，初始平台失准角为[300″300″300″]，陀螺常值漂移为10(°)/h，加速度计常值漂移为1 mg.滤波周期1 s，输出校正周期1 s，从第51 s开始加入反馈校正，反馈校正周期5 s，仿真时间400 s.

实验分为两组:一组为本文给出的基于可观测性的自适应混合校正滤波器;另一组为传统的混合校正滤波器，即反馈因子为αtra=diag{11…1}，其他参数相同.自适应混合滤波器与传统的混合滤波器仿真结果对比如图3～5所示.

图3 平台失准角

图4 速度误差

图5 位置误差

在0～50 s，两个滤波器都没有进行反馈校正，误差有一定的累积，从51 s开始进行每5 s一次反馈校正.传统混合滤波器由于没有考虑系统状态可观测性影响，将状态的估计值无论优劣全部反馈给SINS，可观测性低和不可观测的状态估计盲目对SINS进行不完全正确的修正，容易导致校正过度，使估计误差出现较大范围波动.以陀螺仪常值漂移ε为例，在第400 s时，传统混合校正滤波器针对ε的3个反馈因子分别为1、1、1;自适应混合校正滤波器中对ε的3个反馈因子分别为0.064 1、0.300 7、0.043 2.而事实上，只有与外部观测量直接相关的δv和δR的可观测性最高，反馈因子接近于1，ε的可观测性相对较低，反馈因子小于1;则传统混合滤波器的反馈因子偏离于实际情况，相对于自适应混合校正滤波器来说，对SINS修正效果相对较差，对滤波精度的提高有限.

对于GPS接收机，自适应混合滤波器与传统的混合滤波器仿真结果对比如图6所示.

图6 Ⅰ-Q信号

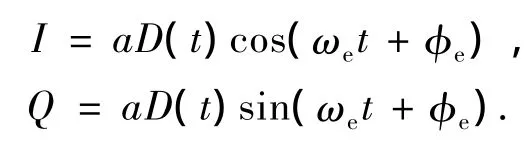
GPS信号变频到中频的频率为ω=4.309 MHz，反馈量由式(9)和式(10)转换为 δⅠ和δQ，对接收机的Ⅰ、Q进行修正，由于信号频率较高，仅根据图6无法比较出两种方法对接收机Ⅰ、Q校正效果的优劣．则可以通过Ⅰ、Q的两个重要特征参数ωe和φe来比较．Ⅰ、Q信号可简写为［17］其中a为信号的幅值，D(t)为数据码．Ⅰ、Q的初相位误差φe和角速度误差ωe与速度误差和位置误差有关，当Ⅰ、Q的初相位误差和角速度误差较小时，测量的速度误差和位置误差会变小．在理想条件下，ωe和φe均为零，则Ⅰ=aD(t)，Q=0，即数据码完全被解调出来，由此测量的速度和位置不存在由于信号解调而引入的误差．因此可以通过比较ωe和φe来比较两种混合校正对接收机的校正效果，即ωe和φe越小，Ⅰ、Q的值就越接近于理想情况，导航定位精度越高．经两种方法校正接收机后，ωe和φe如图7所示(这里没有考虑a的大小)，从图中可以看出，经本文方法校正后的ωe和φe明显小于传统方法的校正结果，即相比于传统方法，自适应混合校正使得ωe和φe进一步减小，从而在信号解调过程中引入的误差更小，进而提高了定位精度．

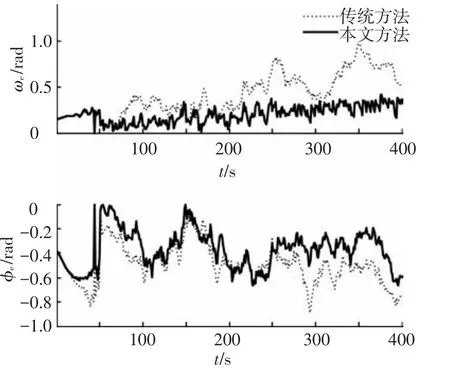
图7 Ⅰ-Q信号的初相位误差与角速度误差

除了估计精度外，系统的实时性是另一个至关重要的因素.若反馈因子计算过于复杂，则系统的实时性势必会降低.实时性的强弱可以间接由参与计算矩阵的维数来反映.如果采用文献［6］中的方法，要计算系统的反馈因子，需要首先计算系统的可观测性矩阵，假设可观测性矩阵的分段时间间隔为1 s，则可观测性矩阵维数为136T ×17，T=1，2，…，400，第400 s时系统可观测性矩阵的维数将达到54 400×17，计算量随着时间的延长而剧增，系统实时性将会遭到严重破坏.而本文方法，无论时间多长，做可观测性分析的误差协方差阵维数始终保持17×17，计算量不随时间的增加而增加，可以有效保持算法的实时性.

5 结语

重新推导了GPS/SINS超紧组合系统模型的量测方程，将Ham提出的特征值和特征向量可观测性分析方法应用于该系统可观测性分析，并利用分析结果制定反馈因子，设计了一种基于系统状态可观测性的自适应混合校正滤波方法.仿真结果表明，该方法可以有效校正惯导和接收机的原始数据，提高系统长时间运行时的导航精度，并且计算量小、实时性好.

［1］秦永元.惯性导航［M］.北京:科学出版社，2006:355-361.

［2］陈帅.精确制导炸弹低成本惯导/卫星组合导航方法研究［D］.南京:南京理工大学，2008:32-54.

［3］林敏敏，房建成，高国江.GPS/SINS组合导航系统混合校正卡尔曼滤波方法［J］.中国惯性技术学报，2003，11(3):29-33.

［4］GOSHEN-MESKIN D，BAR-ITZHACK I Y.Observability analysis of piece-wise constant systems，part I:theory［J］.IEEE Transactions on Aerospace and Electronic Systems，1992，28(4):1056-1067.

［5］GOSHEN-MESKIN D，BAR-ITZHACK IY.Observability analysis of piece-wise constant systems II:application to inertial navigation in-flight alignment［J］.IEEE Transactions on Aerospace and Electronic Systems，1992，28(4):1068-1075.

［6］刘百奇，房建成.一种基于可观测度分析的SINS/GPS自适应反馈校正滤波新方法［J］.航空学报，2008，29(2):430-436.

［7］马艳红，胡军.基于SVD理论的可观测度分析方法的几个反例［J］.中国惯性技术学报，2008，16(4):448-452.

［8］BABU S R，WANG J L，RAO G.Analysis of ultra-tight GPS/INS integrated system for navigation performance［C］//IEEE-International Conference on Signal processing， Communications and Networking.Piscataway:IEEE，2008:234-237.

［9］BABU S R，WANG J L.Ultra-tight GPS/INS/PL Integration:a system concept and performance analysis［J］.GPS Solutions，2008，13(1):75-82.

［10］BABU S R.Ultra-tight integration of GPS/Pseudolites/INS:system design and performance analysis［D］.Australia:The University of New South Wales，2006:67-90.

［11］HAM F M，BROWN R G.Observability，eigenvalues，and Kalman filtering［J］.IEEE Transactions on Aerospace and Electronic Systems，1983，19(2):269-273.

［12］GENG Q B，LI N，LI B K.The application of GPS/SINS integration based on Kalman filter［C］//Proceedings of the 31st Chinese Control Conference.Piscataway:IEEE，2012:4607-4610.

［13］FU L，WANG M.An ultra-tightly MIMU/GPS integrated system and its integrity monitoring［C］//Second International Conference on Instrumentation ＆Measurement， Computer， Communication and Control.Piscataway:IEEE，2012:202-205.

［14］高帅和.分布式GPS/SINS超紧组合架构下的信号处理和信息融合技术研究［D］.哈尔滨:哈尔滨工程大学，2012:3-9.

［15］周卫东，蔡佳楠，孙龙，等.GPS/SINS超紧组合导航系统可观测性分析［J］.北京航空航天大学学报，2013，39(9):1157-1162.

［16］程向红，万德钧，钟巡.捷联惯导的可观测性和可观测度研究［J］.东南大学学报，1997，27(6):6-11.

［17］谢刚.GPS原理与接收机设计［M］.北京:电子工业出版社，2009:281-282.