正弦图合击-分进方法的线段检测技术
杨天博,冯 星,张永强,程丹松,石大明
(1.哈尔滨工业大学航天学院,150001哈尔滨;2.光电控制技术重点实验室,471009河南洛阳;
3.哈尔滨工业大学计算机科学与技术学院,150001哈尔滨)
在日常生活中,大多数是依靠各种线段来定位和识别目标,如房屋的屋檐和道路的边沿,而在图像处理和计算机视觉领域,线段作为对目标定位和识别的重要原始特征,已经被用来解决许多问题,如材料裂缝的检测和卫星图像搜索.然而在许多实际应用中要同时保证速度与精度的要求,如图像引导手术和军事目标跟踪,这意味着需要有更加高效的线段检测方法,因此开发新的方法来快速、准确地提取线段是计算机视觉的一个重要课题[1].
目前现有的线段检测方法可分为3类,即自上而下的方法[2-8],自下而上的方法[9]和空间切换方法[10-12].最常用的自上而下的方法是通过Hough变换来提取直线,然后检测直线端点的位置.文献[3]等利用快速Hough变换获得直线,并将属于各直线的特征点按顺序排列[3],然后根据聚类后特征点的距离来确定线段端点.但是这种方法并不能很好地处理k<-1的线段以及包含多线段的直线,而且Hough变换的参数阈值如果选择不当,还会出现伪线段或线段丢失的现象.
自下而上的线段检测方法是从单独的点开始向上拓展搜索线段.文献[9]则先在大体垂直于线段的方向找到基准对齐点,然后再找到线段作为一个非结构化模型的异常点.但是因为要测试图像中的每一个可能线段,所以非常费时.为了得到快速算法,文献[1]在保留Desolneux方法的同时,通过Helmholtz准则控制伪线段,开发出一个实用的快速线段检测软件.
空间切换方法,一般是在图像空间和Radon极坐标空间进行切换.代表性的方法包括自适应波束特征变换(feature adaptive beam transform,FABT)[10]和文献[11-12]的邻域方法.文献[10]的方法是将Radon变换应用到多尺度方法中来计算FABT.其中自适应特征是指在Radon变换之前应用局部滤波器(如Canny滤波器)进行处理后的特征.它的目的是为了突出图像的线结构进而提高工作的效果和准确性.但是,对于在多尺度分析中尺寸小的图像,该方法的检测精度会下降.文献[11-12]则通过寻找图像空间和参数空间的邻域来改进传统的Hough变换.该方法的难点在于邻域半径的选择,对短线段检测的影响较大.
综上所述,传统的由线到段的提取方法(自上而下)忽略了图像的局部梯度信息,使得提取的线段不精确,而传统的由点及段的提取方法(自下而上)未能考虑全局的信息,使得提取线段的方法容易受噪声干扰.所以为了快速、准确地提取线段,本文在原有研究的基础上[13-14],提出了一个新的空间切换方法“合击-分进法(uniteand-divide,UND)”,在综合考虑图像空间、频率空间及Radon空间全局和局部信息的情况下,首先在傅里叶域利用谱合并方法对线段进行检测,得到它的正弦图,然后在Radon空间对正弦图进行分解得到相应线段.本方法的优点在于通过对正弦图的分解可以对检测的候选区域进行粗定位,从而减少后续线段分割的计算量,提高识别的精度和速度.
1 线段检测的空间切换方法
从机器学习的角度来看,在3个线段检测方法中,自上而下的方法是从参数空间到数据(特征)空间的模型选择技术,而自下而上的方法是从数据(特征)空间到参数空间的正规化技术.但传统的图像空间分析法因忽视了全局信息而造成对噪声的敏感;相反传统的频域分析方法又忽视了图像本身的局部信息而达不到更高的精度要求.所以最佳的解决方案是两者的结合,即自上而下的模式选择和自下而上的正规化,通过在不同的空间进行转换(利用空间切换方法)来获得最佳的效果.时域-频域分析方法就是其中一种方法,它同时考虑了图像空间与频率空间信息,但该方法存在较难描述一些基本特征共性的问题.比如,小波变换就不能利用线段的方向性这一特点,所以不适合线段提取.本文针对以上问题,提出了一种新的空间切换观点,综合考虑多个空间不同特点的信息来进行图像理解与特征提取.
基于空间切换法的图像线段提取方法如图1所示.图像经过傅里叶变换后可以得到频率空间,而在频率空间是完全没有空间信息的.所以本文可以根据特定特征的需要通过另外一种变换作中间媒介,将频率空间与图像空间联系起来.比如,在线段特征提取时,就可以利用投影定理,从频率空间切换到Radon空间,再通过从极坐标映射直角坐标的方法,将此特征切换到图像空间.
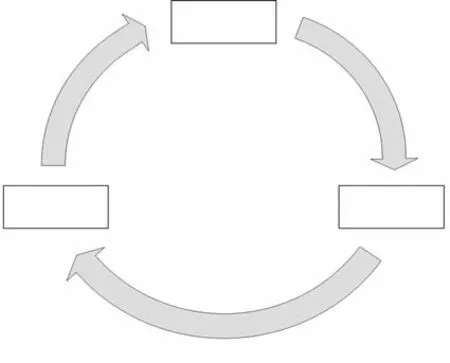
图1 基于空间切换法的图像线段提取方法
2 合击-分进算法
空间切换线段检测方法有两个问题需要解决:1)如何在不增加计算成本的前提下,在傅里叶域大幅增加可分析频率的数量,即精度问题;2)如何快速准确地检测出线段,即速度问题.为了解决这两个问题,本文提出了频谱图与正弦图的合击-分进算法(UND),具体过程如图2所示.
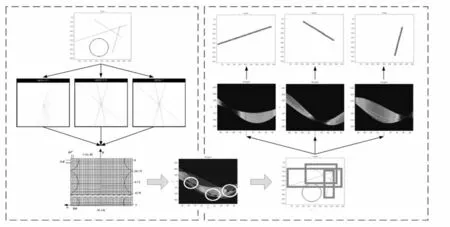
图2 “合击-分进”法图解
2.1 谱的合并
给出一幅N*N的图像,它的多层分数傅里叶变换(MLFRFT)[15]可表示为
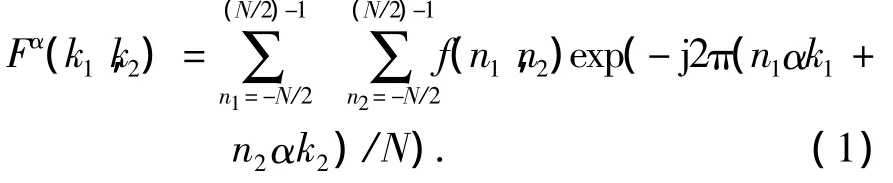
式中{f(n1,n2)|-N/2≤n1,n2≤N/2}为二维离散信号,0<α≤1是实数.
为了提高处理速度,本文采用双参数方法进行多层分数傅里叶变换,表达式为
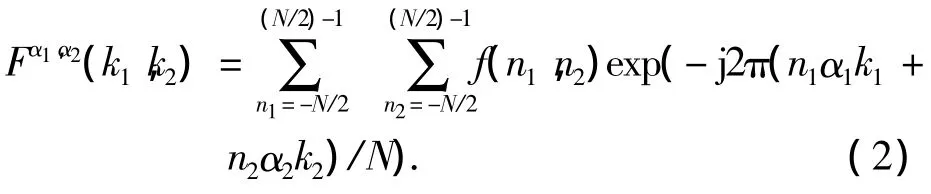
这是因为当α的两个参数不同(如α=(0.1,0.2))时,利用式(1)的计算公式不能直接计算,需要进行两次傅里叶变换,分别计算(0.1,0.1)和(0.2,0.2)处的频谱值,然后通过插值方法计算(0.1,0.2)的数值,而式(2)的计算公式可以直接计算求的,提高了计算速度.
因为本方法主要是检测直线段,所以边界信息十分重要,而边界信息在频谱上对应高频部分,因此αi的取值范围给定为 0.5< α1,α2≤ 1,(Fα1,α2(k1,k2))的 N × N 个频率分布在[- α1π,α2π]×[- α1π,α2π]区间,而且从文献[15]中可知:Fα1,α2(k1,k2)=F(α1k1,α2k2),且根据式(2)使用不同αi条件下的多层傅里叶变换,本文可以得到一组整数以及非整数网格上分布的频率.这一事实表明,人们可以计算非整数网格的频率.这些不同层频率集的并集可以提供更多频谱以供分析.此外如果以原点为中心对频谱作垂直平面切割,并对各切片分别作一维傅里叶逆变换.那么根据投影定理可知,傅里叶逆变换结果等价于Radon变换极坐标域的正弦图,因此多层分数傅里叶逆变换更适合笛卡尔坐标到极地坐标的映射.
此外当对一个N*N大小图像进行处理时,离散傅里叶变换将产生一个N*N个谱.换句话说,它只有N*N个离散频率可用作频域分析;然而在实际处理时可能会出现感兴趣的频率没有落入这些离散频率的情况,这样的问题就是人们常说的“走样”,它将导致使用离散元素捕获或产生的连续信号频率发生模糊.对于本文所处理的线段检测任务,可能会导致在正弦图中产生许多假峰.为了解决这个问题,传统的傅里叶频谱分析方法采用补零(zero-padding)方式[16]来提高精度,即首先在图像周边填充像素值为零的许多点以扩大图像的尺寸,然后对扩大尺寸后的图像进行傅里叶变换进而得到更多的频谱,这种方法显而易见是用时间去换取精度.针对文献[16]存在的问题,本文采用并行的多层傅里叶变换,即利用式(2)计算具有不同αi的MLFRFT来获得更多的频谱信息,在不增加时间成本的条件下,可以实现任何所需的精度.本文这种频谱合击方法与传统的傅里叶变换之间的差异在于,前者具有更高的频率网格,即可以在[-π,π]获得更多的频率而不是仅仅局限于N*N个频率.此外在计算复杂性方面,本文方法也优于文献[16]的方法,对比结果如表1所示.

表1 频谱合并法与补零法的计算复杂性比较(T=O(N2log2N))
2.2 正弦图分解
正弦图的峰值可从前一阶段谱的合并获得.在前一阶段得到的正弦图中检测峰值,其所在Radon空间的极坐标便是直线对于原点的距离及角度.事实上,线段的端点信息都包含在由每个峰为中心的波形正弦图的蝴蝶状边缘线上.
在实际应用时,图像通常会有数十条甚至数百条互相交错的线段,这就造成Radon空间上的蝶形波相互重叠,以致无法找到每条蝶形的边缘线.但是,在前一阶段频谱合击法生成的正弦图上,各峰值还是可以相互清晰地分离的.本文可以利用这一优势,在各峰值周围邻近的蝶翼区中,以找到最外围边沿为原则来确定一个小区域(窗口).在该邻域内虽不能区分究竟有多少条线段,但可以在屏蔽掉此图像窗口上非直线方向的像素后,再做 Radon变换,进而得到一条清晰的正弦图.
频谱图与正弦图的合击-分进算法的具体执行步骤如下:
1)谱合并.利用式(2)针对不同的αi值计算一定数目(所要查找线段的个数)的傅里叶变换,并把它们合并到一个联合谱中.本步骤对应图2左下部①.
2)傅里叶域到Radon域的转换.利用线性插值算法把合并谱从笛卡尔坐标网格映射到极坐标网格,并用一维FFT逆变换返回谱域.根据中心切片定理,每个一维FFT逆变换对应Radon空间的一个正弦.本步骤对应图2中下部②.
3)正弦分解.检测正弦中的最大峰值,它对应图像中的直线,每个直线可以包括多个线段.本步骤对应图2右下部③.
4)Radon域到图像域的转换.Radon域正弦中的每个峰值都对应图像域中的一条直线,沿着每个窗口的对角线应用高斯滤波器,获得线段的主方向.
5)分割正弦图的线段检测.根据在步骤4)中获得每个子窗口的正弦图.分析蝶形波的不连续性进行线段检测.每个蝶形波边缘对应线段的端点.本步骤对应图2右上部④.
6)重复步骤4)、5)处理,直到所有的蝶形区都被检测出来.
7)结束.
3 实验结果
通过对混合不同粗细线段的图像和自然图像的实验来验证本文方法的准确性、抗噪声能力和计算时间的复杂性.
3.1 精度的验证
实验的目的是要表明,UND方法可以对宽度大于一个像素且没有预先进行边缘检测的线段进行检测.图像的测试过程如图3所示,表2给出了检测到的线段的信息和对比结果,包括到原点的距离,与原点的角度和两个端点 (x0,y0),(x1,y1)的位置.原点坐标设置在图像的左下方.表2给出了检测误差,数值为与端点(x0,y0),(x1,y1)差值的绝对值(就是真正端点坐标和检测端点坐标之间的差异).对比结果表明,UND方法能够从图像中准确的检测出不同宽度的线段.
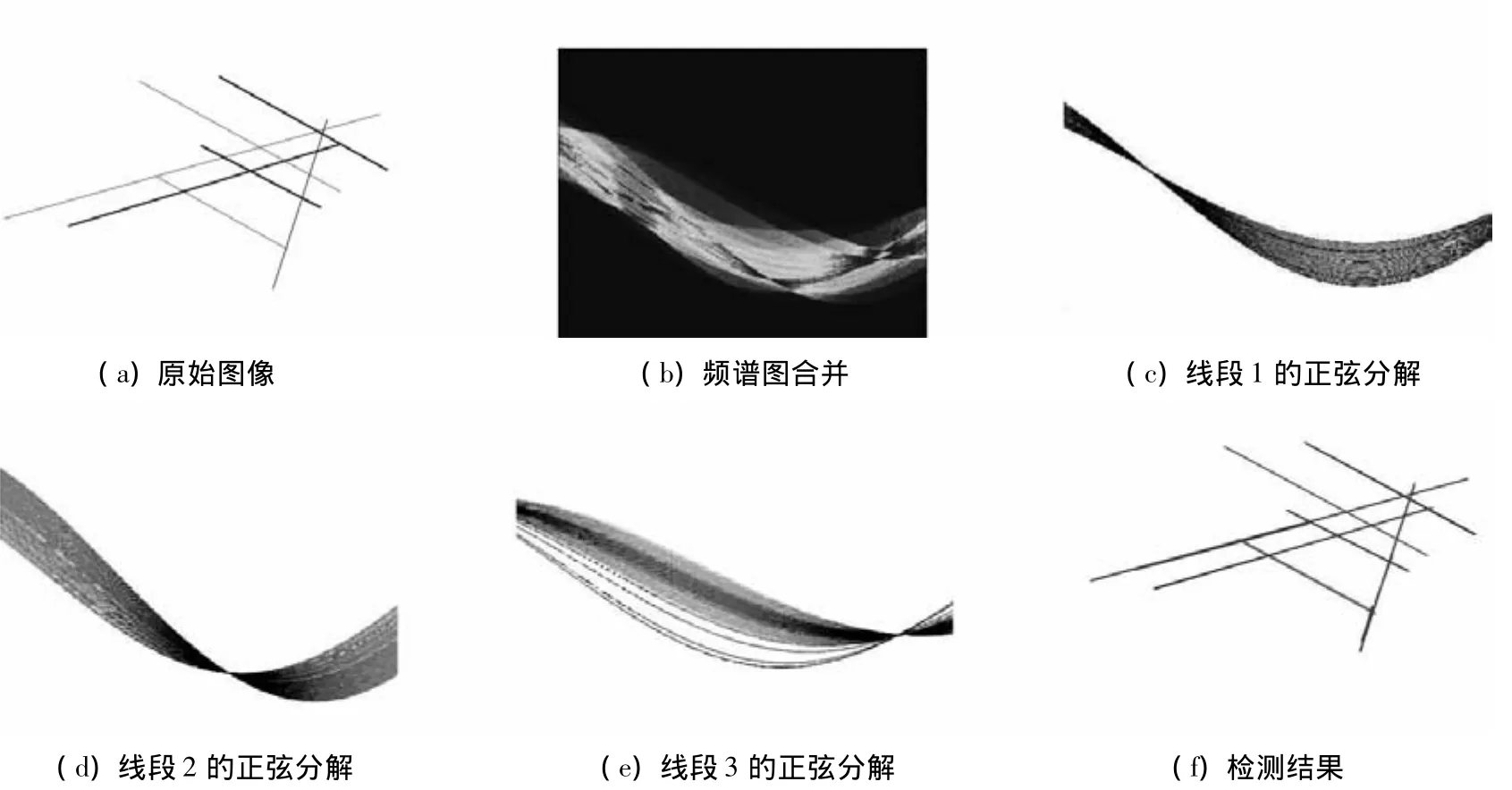
图3 不同粗细线的图像
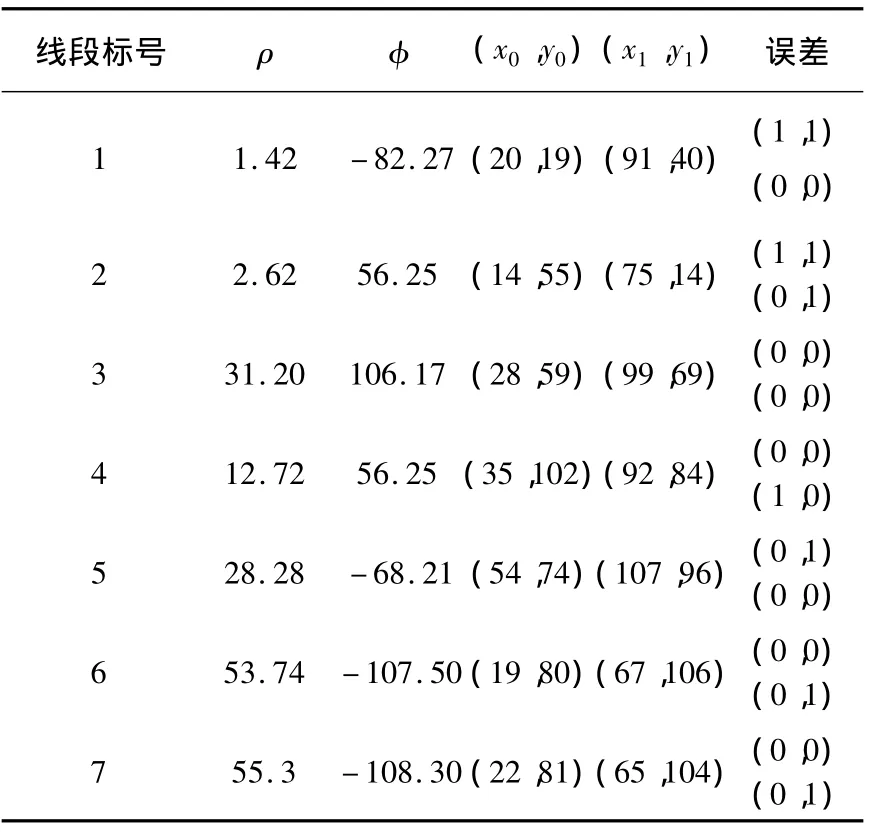
表2 合击-分进法的线段位置检测
3.2 算法的抗噪性
因为 UND方法在谱的合并阶段,同文献[13]的执行步骤相似,也是按照依次经过二维并行多层傅里叶变换、直角坐标至极坐标映射、一维傅里叶逆变换等处理后得到它的正弦图.所以本算法的抗噪性能力同文献[13]的效果相同,效果如图4所示.
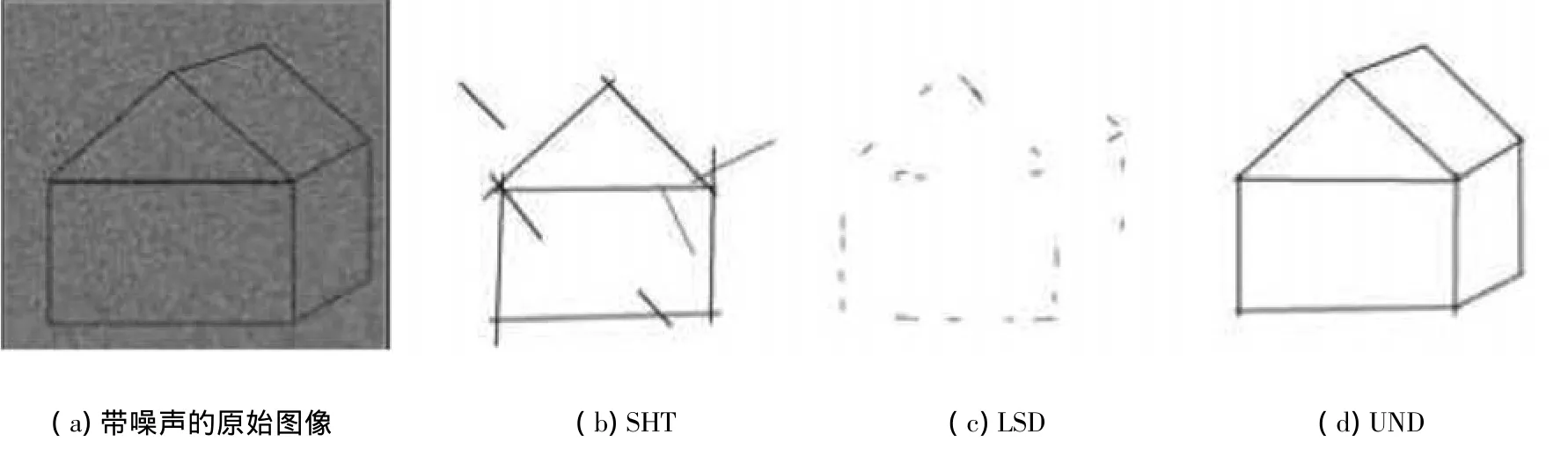
图4 带噪声图像的线段检测

图5 几种代表性线段检测方法的性能比较
由图5可知,LSD方法相对于其他方法在速 度方面拥有优越的性能,但对一些细节如短线段
3.3 对自然图像进行线段检测
本文使用文献[1]中的自然影像来评价UND方法对线段检测性能.在这个实验中,SHT[17]和UND的峰阈值被设置为0.8*pmax,其中,pmax为正弦图中的最大峰值.本实验的主要目的是把UND方法与几个具有代表性的方法,如SHT、RHT[18]和LSD,在计算时间和线段检测结果等方面进行比较,比较结果如图5所示.的检出率不高.所提出的UND方法在综合性能方面是整个Hough变换家族中最好的;在检测细节方面(短线段)强于其他方法.这是因为在SHT和RHT方法中,只是简单的根据连通性来分割线段.此外RHT因为它的随机抽样策略不能检测短线段;SHT因为它的边缘方向信息没有用于线段检测,所以往往会产生虚假的检测结果.此外在对噪声的鲁棒性问题方面,通过对含有噪声的图像进行实验,UND方法表现出很好的效果,这是因为它对于线段的突然连接/断开是不敏感.然而在实验上也反映出一些问题,当部分短线段和噪声比较接近时,很容易受到其他前景像素的影响,在正弦图中可能不会形成明显的峰值,这也是为什么UND无法检测到部分短线段的原因.
在图6中显示了与邻域 HT[12]等方法相比较,UND方法在短线段检测方面的优越性能.这是因为邻域HT方法会遇到半径大小选择的问题,如半径选择过小将不能覆盖整个线段,选择过大将导致线段丢失;而且与长线段相比,短线段还会存在较大的近似误差,所以在短直线检测方面的效果并不好,这种现象在图6(c)中的卡车图像表现得非常明显.对比图6(b)、(d),可以看出LSD方法比UND方法能获取到更多的短线段,但有时它会把一条长线段分割成若干段,使直线不能保持连贯性.此外,在速度方面,RHT是Hough变换家族中最快的,本文的UND方法次之.
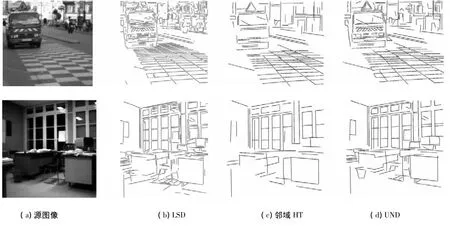
图6 自然图像的处理结果
4 结论
1)提出了一种称为正弦图合击-分进(UND)的空间切换的线段检测方法,它包括两个阶段:进行频域的频谱合并,并在谱合并后进行Radon变换展开;进行Radon空间的正弦图分解,进而在分离后的正弦图中进行线段检测.
2)由于可以并行实施合并和分解,本方法具有较低的时间计算成本.
3)通过对自然图像的实验测试可以看出,本文提出的UND方法在性能上优于SHT、RHT和LSD等经典线段分割方法,具有较高的线段检测精度,同时降低了计算成本,增强对噪音干扰的鲁棒性.
[1]von GIOI R G,JAKUBOWICZ J,MOREL J M,et al.LSD:a fast line segment detector with a false detection control[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(4):722-732.
[2]左磊,李明,张晓伟,等.基于改进Hough变换的海面微弱目标检测[J].电子与信息学报,2012,34(4):923-928.
[3]GUERREIRO R F C,AGUIAR P M Q.Connectivityenforcing hough transform for the robust extraction of line segments[J].IEEE Transactions on Image Processing,2012,21(12):4819-4829.
[4]胡静,张天序.基于速度估计的双Hough变换运动轨迹检测算法[J].华中科技大学学报:自然科学版,2013,41(1):106-110.
[5]阿布来提·依布拉音,王治强,刘薇,等.基于Hough直线检测的深度图像配准方法[J].中国科学院研究生院学报,2013,30(1):112-116
[6]LI Weichen,TSAI Duming.Defect inspection in lowcontrast LCD imagesusing Hough transform-based nonstationary line detection[J].Industrial Informatics,2011,7(1):136-147.
[7]GUERREIRO R F C,AGUIAR P M Q.Connectivityenforcing Hough transform for the robust extraction of line segments[J]. IEEE Transactionson Image Processing,2012,21(12):4819-4829.
[8]SERE A,SIE O,ANDRES E.Extended standard hough transform for analyticalline recognition[C]//Proceedings of 6th International Conference on Sciences of Electronics,Technologie of Information and Telecommunications(SETIT).Sousse:IEEE,2012:412-422.
[9]BURNS J B,HANSON A R,RISEMAN E M.Extracting straight lines[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1986,8(4):425-455.
[10]BERLEMONT S,OLIVO-MARIN J C.Combining local filtering and multiscale analysis for edge,ridge,and curvilinear objects detection[J].IEEE Transactions on Image Processing,2010,19(1):74-84.
[11]DU Shengzhi,van WYK B J,TU Chunling,et al.An improved Hough transform neighborhood map for straight line segments[J]. IEEE Transactionson Image Processing,2010,19(3):573-585.
[12]DU Shengzhi,TU Chunling,van WYK B J,et al.Collinear segment detection using HT neighborhoods[J].IEEE Transactions on Image Processing,2011,20(12):3612-3620.
[13]SHI Daming,ZHENG Liying,LIU Jigang.Advanced Hough transform using a multilayer fractional Fourier method[J].IEEE Transactions on Image Processing,2010,19(6):1558-1566.
[14]ZHENG Liying,SHI Daminjg.Advanced radon transform using generalized interpolated Fourier method for straight line detection[J]. ComputerVision and Image Understanding,2011,115(2):152-160.
[15]PAN Wei,QIN Kaihuai,CHEN Yao.An adaptable-multilayer fractional Fourier transform approach for image registration[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(3):400-414.
[16]HO C G,YOUNG R C D,BRADFIELD C D,et al.A fast Hough transform for the parametrisation of straight lines using Fourier methods[J].Real-Time Imaging,2000,6(2):113-127.
[17]庞存锁,侯慧玲,韩焱.基于霍夫变换的高速微弱目标检测算法[J].电子与信息学报,2012,34(3):754-757.
[18]XU Lei,OJA E.Randomized Hough transform-basic mechanisms, algorithms, and computational complexities[J].CVGIP:Image Understanding,1993,57(2):131-154.

