具有初始弯曲的1000 MW汽轮机低压转子的振动特征分析
吴文青,谢诞梅,杨 毅,胡鹏飞
(武汉大学 动力与机械学院,武汉 430072)
弯轴事故可能发生在转子的运输、安装或者使用过程中。虽然对大部分的旋转机械而言,转子弯曲(包括热弯曲和初始弯曲)的幅度都非常微小,有时甚至可以忽略不计,但是,对于需要长期运行的大型汽轮发电机组而言,由于其轴系跨度大、且转子直径大,其细微变化都将严重影响轴系的稳定性。运行中,转子的弯曲可以由很多因素引起:工况快速变动中产生的热变形、转子受到冷热交替的冲击、碰磨、摩擦部位的热效应、轴系刚度的改变等。研究成果表明,弯轴引起的振动响应状态与传统的由于质量不平衡造成的和转速变化一致的振动响应非常相似,二者仅在振动幅值和相位角上存在着一些微小的区别,特别在极低速或极高速情况下这种区别比较明显。对于有初始弯曲的转子,当转速接近0时,振幅接近初始弯曲值;反之,在高转速下,因为弹性变形与弯曲变形呈180°反向,振幅趋于0。几十年来,学者们对初始弯曲故障引起的转子振动现象进行了深入的研究。林富生等[1]研究了有初弯的刚度非对称转子的动力学特性,并进行了相关实验。罗廷等[2]研究了具有初始弯曲的多圆盘转子系统的一阶振动特性。Nicholas等[3]通过理论和实验的方法研究了弯轴状态下挠性转子的不平衡响应;Parkinson等[4]指出转子在弯轴和质量不平衡下具有不同的振动响应;Shiau等[5]研究了残余弯曲对具有倾斜轮盘和不平衡质量的简化轮盘-转子系统的动力学响应的影响;Edwards等[6]则给出了通过测量转动信号确定转子弯曲和弯曲形状的模态分量判断法。上述文献没有涉及交叉刚度、回转效应、剪切模量和惯性效应等,而这些因素对大型汽轮机转子的影响不容忽视。
1 000 MW超超临界机组凭借良好的运行性能在中国得到快速发展。然而,运行经验显示,很多1 000 MW超超临界汽轮发电机组都存在振动偏大的现象,特别是低压转子的振动比较突出。资料显示,在机组的调试和运行初始阶段,低压转子的弯轴故障越来越突出。造成这种故障的原因可能是由于低压转子存在着不均匀的温度场,而不均匀的温度场可能是由于机组启停过程中温度的快速增加/减少所造成。针对这一问题,本文选取某1 000 MW超超临界汽轮机的低压#2转子为研究对象,研究其在具有初始弯曲状态下的振动特性[7]。图1给出了低压#2转子-轴承系统的结构图,在建立有限元模型时考虑了轴系的回转效应、剪切弹性模量、转动惯量。整个转子被划分为46个节点。计算中,取两轴承处的初始支撑刚度相同(kxx=kyy=2.45×109N/m)、阻尼相同(cxx=cyy=3×103N·s/m)。

图1 低压#2转子-轴承系统模化Fig.1 Modeling of a LP B rotor-bearing system
1 模态分析
对于一个多自由度的转子-轴承系统,其振动方程通常按如下方程描述:
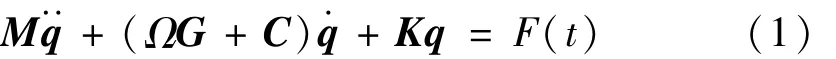
式中:q为广义坐标系下的单位矢量;M为质量矩阵;G为回转矩阵;C为阻尼矩阵;K为刚度矩阵;Ω为转子旋转速度;F(t)为合力。
1.1 自由振动
对于自由振动,F(t)=0。此时,方程(1)的状态空间表达可以写成[8]:

一阶微分方程的空间矢量X={q q·}T是

因此,自由振动的解可以写成如下形式:

式中,X0是复矢量,s是复标量。将式 (4)代入式 (3)并整理得:

因指数不为零,故

式(6)是特征值的求解问题,其解有2n对共轭复数:

式中:si为第i模态的特征值,它以共轭复数的形式出现;ωni、ωdi、ζi分别为固有频率、固有阻尼频率和阻尼系数。
1.2 不平衡响应
作用在节点k上的广义力矢量可以用偏心轮盘的偏心距离ε和偏心角度β表示[6]。

式中:δ和γ分别是t=0时在Oxy轴平面产生的外部不平衡力和力矩的大小。将方程(8)代入方程(1)即有:

其稳定解可以通过假设 q(t)=R(q0ejΩt)求得(其中q0为复数)。因此

1.3 弯轴响应
对于一个弯曲转子,其运动方程可以写成[6]

式中:qe为节点处的弹性弯曲矢量;q为该节点处总的弯曲矢量。因此有q=qe+qb,其中qb表示带有初始弯曲的转子在静止状态下弯曲矢量,由此可得qe=qqb。因此,方程(11)可以改写成

弯曲转子的各几何截面的详尽定义如文献[9]所述。因为转子旋转,所以描述弯曲转子状态的方程是时间的函数,于是有 qb(t)=R(qb0ejΩt)其中 qb0为复数。因此

令其解的形式为 q(t)=R(q0ejΩt),则

2 计算结果
2.1 转子固有频率
表1给出了转子在0 r/min和3 000 r/min之间的前8阶固有频率(特征值)。转速为0时,固有频率成对出现,这是因为转子在x方向和y方向的惯性及支持刚度完全相同。当转速达到3 000 r/min时,在回转效应的作用下,每一对固有振动频率会发生分离现象。其原因是该转子及其轮盘的直径大而导致回转效应的影响也大。需要说明的是,因方程根的实部非常小,其阻尼系数近似为0,因此有阻尼的固有频率与无阻尼的固有频率非常接近。

表1 前8阶的特征值及对应的固有频率Tab 1.The first eight eigenvalues and natural frequencies0 rev/min3000 rev/minRoot s
2.2 案例分析
2.2.1 案例 1:转子的支撑各向同性
(1)不平衡响应
假设在转子11号和31号节点(图1所示)上的相同相位角位置各附加一个大小相同的不平衡质量(0.001 m)。图2给出了施加不平衡质量后x方向上的不平衡响应(因为转子是轴对称,所以其在x方向和y方向的响应一致)。由图可知,在转速为1 360、2 750和3 680 r/min时转子的不平衡响应达到最大值。比较发现,这几个转速和转子的前三阶固有频率基本一致,只有正进动。当转子过临界转速时,相位角几乎产生了180°的改变(由于阻尼的存在,相位角的变化不完全等于180°)。而当转速低于2 240 r/min之前,2节相位相同。在共振转速和反共振转速2节点的相位角都会发生翻转。11号节点处的相位角在转速为2 250 r/min时由约180°翻转至约 -180°,而在2 890 r/min时又由约-180°翻转至约180°;31号节点处的相位角在转速为3 050 r/min时由约180°翻转至约 -180°。

图2 转子11、31号节点x方向的不平衡响应Fig.2 Unbalance response of the rotor at node 11,31 in the x direction
(2)弯轴响应
本文在计算弯曲转子的不平衡响应时,首先通过有限元计算得到转子的初始弯曲值,Christopher等[9]对此有过详尽的论述。图3给出了通过有限元模型获得的阶梯轴在垂直平面的挠曲变形分布。转子上施加了轮盘和转子的质量力。
图4给出了转子系统对在初始弯曲不平衡力作用下、在11、31号节点处的振动响应。

图3 阶梯轴在垂直平面的挠曲变形分布Fig.3 Stepped shaft deflection in vertical plane

图4 弯轴状态下转子11号、31号节点x方向上振动响应Fig.4 The response of the rotor at node 11 and node 31 in x direction due to a bent rotor
与图2中因不平衡力而产生的响应相比,虽然二者的响应结果非常相似,但在转子的低速区和高速区存在着细微差别:首先,在转速为2 670 r/min附近时,转子的11号节点处的响应值为0;其次,11和31号节点在第二、第三峰值处均未出现反共振;第三,最大响应分别发生在转速为 1 360 r/min,2 750 r/min和3 680 r/min时,这与不平衡力引起的转子最大响应值一致;最后,11号节点处的相位角在2 170 r/min时由约180°翻转至约 -180°,而31号节点处的相位角在2 870 r/min时由约 180°翻转至 -约 180°。
2.2.3 案例 2:转子的支撑各向异性
对同一轴系,本文还计算了轴承支撑刚度变化的影响:即在其他参数不变的条件下,将其轴承支撑方式改变为各向异性,轴承的初始支撑刚度给定为kxx=2.45×109N/m及 kyy=2.00×109N/m。
(1)不平衡响应
在上述条件下,同样假设在转子11号和31号节点(图1所示)上的相同相位角位置各附加一个大小相同的不平衡质量(0.001 m)。此时的不平衡响应如图5所示。
由图5可知,当转子转速为 1 340、1 360、2 620、2 760、3 360和3 670 r/min时响应达到最大。此外,在这种条件下,转子同时出现正进动和反进动现象。
由于系统x、y方向的支撑刚度不一样,造成了这两个方向上涡动幅度不一样,如图6和图7所示。

图5 转子11号、31号节点x方向上不平衡力作用下的响应(椭圆长轴方向)Fig.5 Response of the rotor at node 11 and node 31 in x direction due to out-of-balance force at node 11 and node 31(the length of the semimajor axis of the orbit)

图6 11号节点处x、y方向上的振动响应,着色区域为反进动Fig.6 Response in x and y direction at node 11.The shaded region indicates backward whirl

图7 31号节点处x、y方向上的振动响应,着色区域为反进动Fig.7 Response in x and y direction at node 31.The shaded region indicates backward whirl

图8 弯曲转子11、31号节点处x方向上的振动响应Fig.8 The response of the rotor at node 11 and node 31 in x direction due to a bent rotor
仔细观察图6和图7不难看出,在x和y方向的振幅最大响应处,相位的响应也发生改变,但x方向上相位角的变化跟y方向上相位角的变化并不一致。图6和图7中的着色区域表示反进动的转速区域(所对应的x和y方向的相位响应不同)。由此可知,在某些转速区域,转子的一些部位进行反进动运动而另外一些部位进行着正进动运动(交叉模态)。
(2)弯轴的响应
对于弯曲转子(图3所示),其11、31号节点处振动幅值和相位角的响应如图8所示。可以看出,在转速为1 340 r/min和1 360 r/min区域存在着两个峰值,同时存在着正进动和反进动。
图9和图10给出了节点11和节点31处x、y方向上振动响应。图中阴影区域表示反进动的转速区域(所对应的x和y方向的相位响应不同)。

图9 弯曲转子11号节点处x、y方向上的振动响应Fig.9 Response in x and y direction at node 11 due to a bent rotor

图10 弯曲转子31号节点处x、y方向上的振动响应Fig.10 Response in x and y direction at node 31 due to a bent rotor

图11 各向异性支撑下弯曲转子11(虚线)、31(实线)号节点处涡动轴心轨迹(×表示轨迹的起点,◇表示轨迹的终点)Fig.11.Whirl orbits at node 11(dashed)and node 31(sdid)for the bent rotor on anisotropic bearings.The cross denotes the start of the orbit and the diamond denotes the end
与不平衡响应类似,在某些转速区域,转子的一些部位进行反进动运动而另外一些部位进行着正进动运动,不同的是,所对应的转速范围不同。图11给出了这2个节点在不同转速下的轴心轨迹图。由图可知,在上述条件下,这些轴心轨迹呈椭圆形,可能是正进动也可能是反进动。
3 结 论
本文研究了1 000 MW超超临界汽轮发电机组低压#2转子在不平衡力和弯曲状态下的振动瞬态响应,所得结论如下:
(1)由不平衡力和转子弯曲激发的转子振动响应特征虽然非常相似,但是仍然有着轻微的差别;
(2)转子在定速下旋转会出现因质量不平衡或弯曲而产生的涡动,当转子支撑在各向同性轴承上时,无论是激振力是正向或反向涡动,所引起的振动响应均为正进动;
(3)而当转子支撑在各向异性轴承上时,无论是激振力是正向或反向涡动,所引起的振动响应均将是为反进动。
[1]林富生,孟光.有初弯的刚度非对称转子的动力学特性分析及实验研究[J].应用力学学报,2002,19(3):96-101.
[2]罗廷,刘淑莲,郑水英.具有初始弯曲的多圆盘转子系统的动力学特性分析[J].振动与冲击,2010,29(S):173-175.
[3]Nicholas J C,Gunter E J,Allaire P E.Effect of residual shaft bow on unbalance response and balancing of a single mass flexible rotor-part 1[J].Journal of Engineering for Power,ASME,1976,98(2):171-178.
[4]Parkison A G,Darlow M S,Smalley A J.Balancing flexible rotating shaft with initial bend[J].AIAA journal,1984,22(5):683-689.
[5]Shiau T N,Lee E K.The residual shaft bow effect on dynamic response of a simply supported rotor with disk skew and mass unbalances[J].Journal of Vibration,Acoustic,Stress and Reliability in Design,ASME,1989,111(2):170-178.
[6]Edwards S,Lees A W,Friswell M.I:The Identification of a rotor bend from vibration measurement[C]//Proceedings of the International Modal Analysis Conference-IMAC,1998,V2:1543-1549.
[7] Luo J,Liu Z,Shi Y,et al.The research on supporting stiffness of LP rotor of ultra-supercritical turbine[C]//The 2nd International Conference on Electrical and Control Engineering,IEEE,2011:1846-1848.
[8]Friswell M I,Penny JE T,Garvey SD,et al.Dynamics of rotating machines[M].New York,Cambridge University Press,2010.
[9]Christopher D W,Michael W R.Shaft deflection-a very,very long example [C]// ASEE Southeast Section Conference,2013.
[10] Ngo V T,Zhang Heng-liang,Xiong Yang-heng,et al.Dynamic analysis of a rig shafting vibration based on finite element[J].Front.Mech.Eng.2013,8(3):244-251.

