基于功率法的TMD系统参数优化与减振性能分析

李祥秀，谭 平，刘良坤，张 颖，闫维明，周福霖，

（1．北京工业大学 建筑工程学院，北京 100124；2．广州大学 工程抗震研究中心，广州 510405）

TMD作为一种减振消能装置，性能稳定可靠，适用范围广，因此，在结构减振控制中受到较多的关注。目前已经有不少高层建筑及高耸结构成功运用TMD来控制结构的振动［1］。欧进萍等［2］结合我国现行风荷载规范，研究了设置TMD、TLD控制系统的高层建筑风振分析与抗风设计的实用方法；李春祥等［3］对TMD－高层钢结构系统的风振舒适度的控制设计方法进行了研究，并推到了TMD－高层钢结构系统的传递函数和减震系数的表达式；李创第等［4］对带TMD的高层建筑风振响应问题进行了系统研究，用复模态理论获得了结构风振响应的解析解，并证明此方法可用于对带TMD结构的风振与抗风可靠度分析及基于可靠度约束的抗风优化设计。

近年来，结构振动的能量分析方法在土木工程领域受到广泛关注，该方法克服了传统方法的局限，从能量角度分析了地震对结构的作用。Housner［5］于20世纪50年代提出了能量法的概念，并将其引入到结构控制中。谭平等［6］基于能量原理分析了TMD系统的减振性能，并指出TMD系统对中长周期结构有很好的能量控制效果；卜国雄等［7］基于能量法优化设计了TMD参数，以主结构在整个地震过程中吸收的能量最小为优化准则，考虑了主结构阻尼比的影响，通过非线性规划的数学方法得出TMD的最优频率比和最优阻尼比。以往对于TMD系统的研究，多侧重于研究主结构峰值响应的减振效果以及从能量方面分析系统的减振机理。本文提出功率法，从功率的角度研究了主结构在附加TMD后，结构在地震激励下的减振效果，并考虑了结构周期和阻尼比的影响。同时分析了以主结构耗能功率最小为优化目标时TMD的最优频率比及阻尼比，并与以往的四种优化方法进行了对比。

1 结构－TMD系统的功率平衡方程

本文基于结构－TMD系统的运动方程，提出结构－TMD系统的功率平衡方程。因功率综合考虑传到结构上的力和速度两个量值，同时功率也表示能量对时间的微分，因此和瞬时能量相比，更能贴切地表示结构实时能量的转移与流动。

1．1 运动方程

将结构简化为单自由度体系如图1所示，TMD安装在结构顶部，其运动方程为：

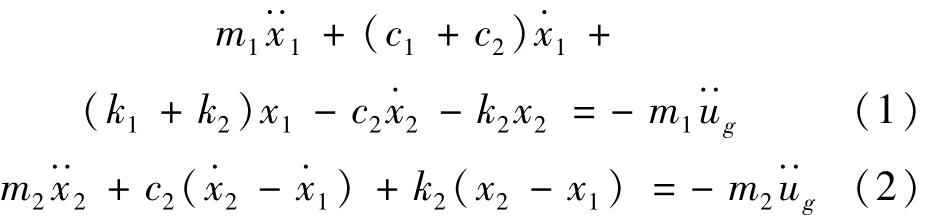
其中：m1，c1，k1为主结构的质量、阻尼和刚度；m2，c2，k2为TMD的质量、阻尼和刚度分别为主结构和TMD相对于地面的加速度、速度和位移；为 地面加速度。

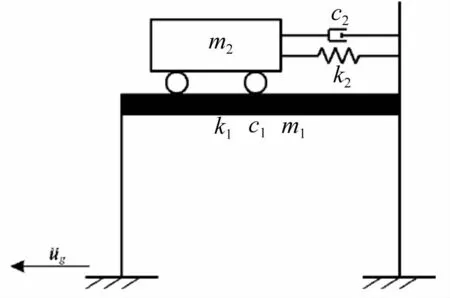
图1 单自由度体系模型Fig．1Single-DOFmodelofsystem

1．2 功率平衡方程

根据功率法的原理，对式（1）两边同时乘以相对速度变量，可得：

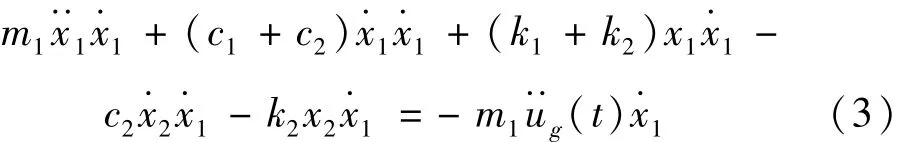
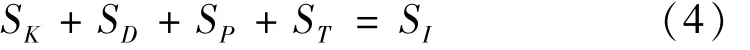
上式中，定义：为主结构的动能功率，S＝D为主结构的自身耗能功率为主结构的弹性功率为TMD转移的功率简称为转移功率为输入功率。

由式（4）可知，结构设置TMD装置后，主结构的部分功率被TMD所转移，从而减小了主结构的功率响应。

2 结构－TMD系统的功率响应分析

假定TMD系统的主结构周期1s，阻尼比0．02，主结构的质量1000t，TMD与主结构的质量比为0．03，TMD的频率比和阻尼比采用DenHartog公式来选取，分别为0．97、0．1。本文选用ElCentro波为地震激励，持时30s，峰值为100gal。其傅里叶图如图2所示。

Hilbert-Huang变换是一种有效的时频分析方法，它建立一套不受傅里叶变换理论束缚，又区别傅里叶谱的方法。本文基于HHT变换得到地震波的时频图如图3所示。

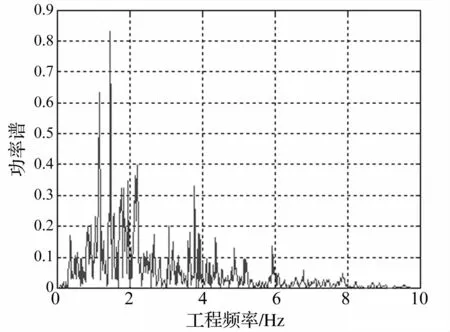
图2 频谱图Fig．2Frequencyspectrumofgroundmotion

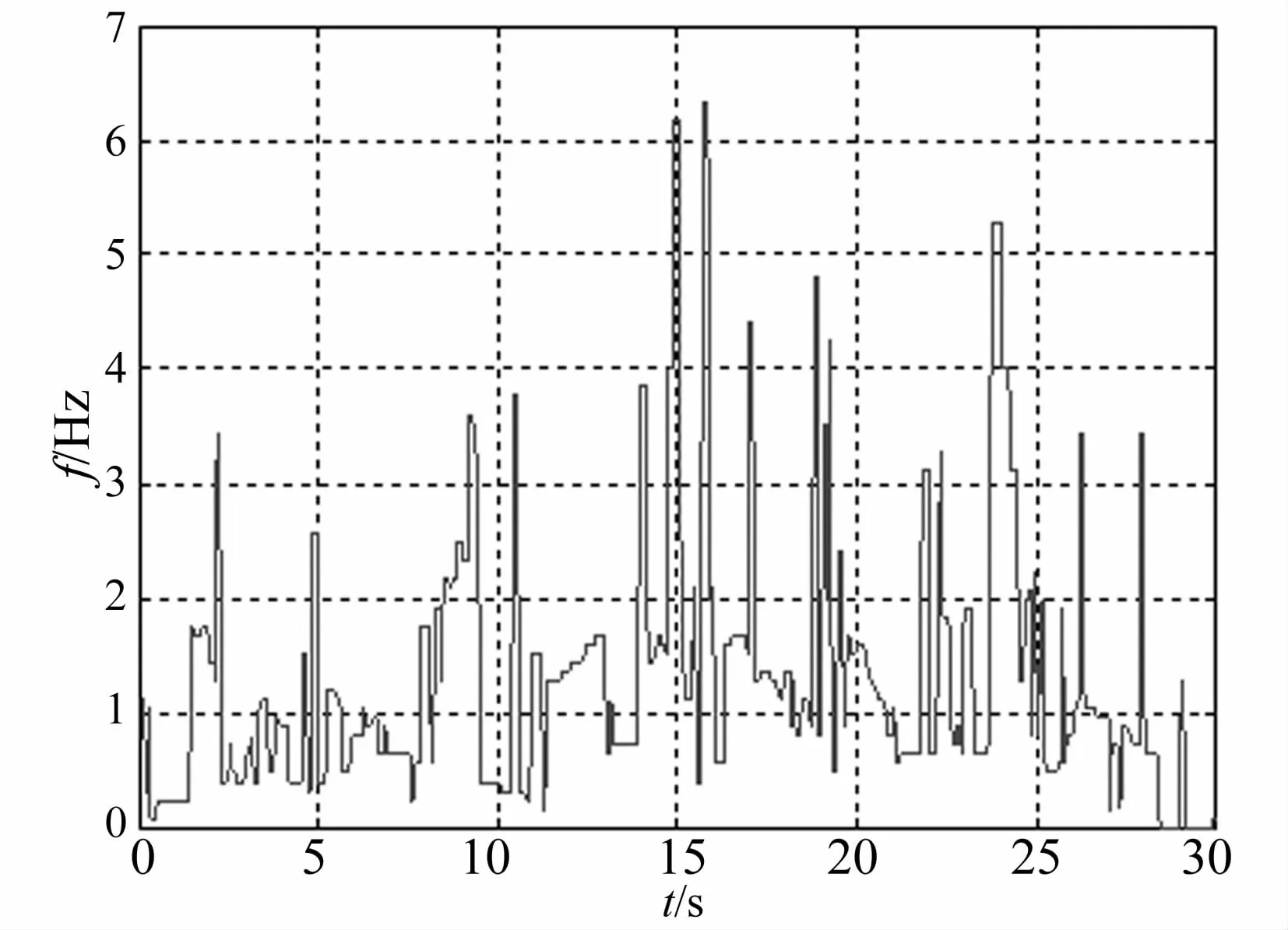
图3 时频图Fig．3Time-frequencyofgroundmotion

2．1 结构体系功率响应分析

从无控结构与TMD系统主结构位移响应及加速度响应对比图（图4）可以看出，TMD系统有一定的减振效果，但在地震动初始阶段控制效果不明显。

TMD系统的功率响应分布如图5所示。由图可以看出，结构的各种功率均在0～15 s内占据一定的成分，在15 s之后则迅速衰减并渐趋于零值。这主要是因为：El Centro波在初始阶段脉冲运动比较强烈，结构的位移、速度和加速度响应在0～15 s均比较大，15 s之后则迅速衰减。另外，结构的输入功率、弹性功率及动能功率均出现负值，这是由地震力做负功引起的。同时，文献［12］从能量方面对此作了解释。

结构在安装TMD装置后，结构的总输入功率、总弹性能功率、总动能功率及主结构的耗能功率均有减少，峰值减小百分比分别为 0．14、0．19、0．31、0．36。这是因为主结构在附加TMD后，主结构带动TMD运动，TMD转移了主结构的部分功率，从而提高了结构的抗震安全性。

由图3可以看出，El Centro波在10～15 s的频率主要集中在0．5～0．8 Hz和1．2～1．8 Hz之间，即外激励频率与主结构的频率比在0．5～0．8和1．2～1．8之间（主结构的工程频率为1 Hz），而由TMD的减振原理图（图6）可知，当外激励频率与主结构的频率比在0．5～0．8和1．2～1．8之间时，TMD系统与无控时相比放大了结构的响应。因此，结构的各功率响应在10～15 s时有控较无控均有放大现象。同时由图5可以看出不同功率的减振效果不同，这是由TMD系统对结构的位移、速度和加速度的减振效果不同引起的。

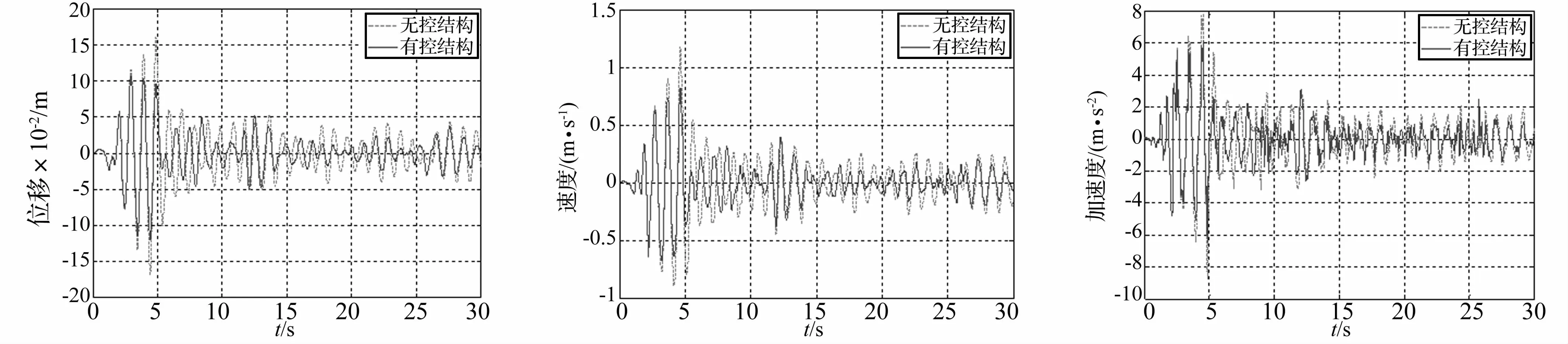
图4 位移、速度及加速度时程响应Fig．4 Time history of structural displacement，velocity and acceleration

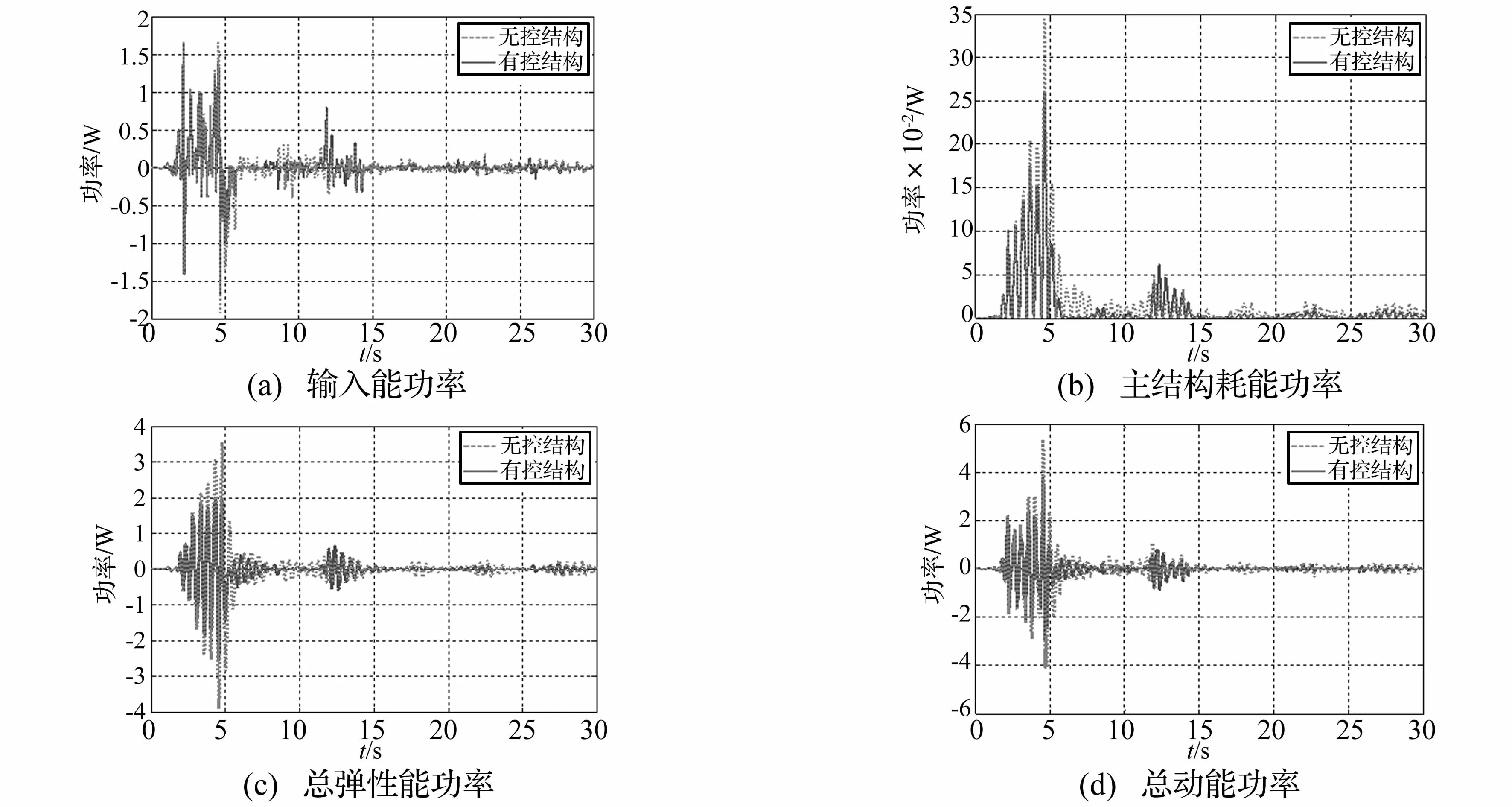
图5 结构功率响应对比Fig．5 Comparison of structural power history responses

2．2 主结构周期的影响

取主结构周期变化范围为0～10 s，主结构的质量为1 000 t，主结构的阻尼比为0．02，TMD与主结构的质量比为0．03，采用 Kannai－Tajimi谱随机地震动模型进一步研究主结构耗能功率均值随周期的分布与变化规律。取Ⅱ类场地，谱强度S0＝0．078，场地圆频率为 wg＝15．71，场地阻尼比为 ζg＝0．72。

结构耗能功率均值随周期的变化如图7所示。与无控结构相比，TMD系统主结构的耗能功率均值的峰值明显减小。同时由图8可以看出，当结构周期在0～0．2 s左右时，有控结构的耗能功率均值较无控结构有放大的现象，对于结构周期在0．2～10 s时，有控结构较无控结构的耗能功率功率比值均小于0．5，这说明TMD系统除了对于特别刚性的结构（T＜0．2 s）之外，都有减振效果。

2．3 主结构阻尼比的影响

主结构周期变化范围为0～10 s，分别考虑主结构的阻尼比为 0．02、0．05、0．08，TMD与主结构的质量比为0．03，研究结构在El Centro波（取自Ⅱ类场地）作用下主结构的阻尼比对各功率响应的影响。

不同阻尼比情况下，TMD系统各功率响应的峰值如图9所示；主结构的阻尼比对总输入功率峰值影响较小，仅在与地震波频率相近时才有所波动，并且结构的总输入功率随阻尼比增大而减小；TMD系统主结构的耗能功率随着阻尼比的增大而增大，且受主结构阻尼比的影响较大；TMD系统转移的功率随着阻尼比的增大而减小，这是因为增大主结构的阻尼，结构自身阻尼耗能必然增加，这虽能较好的较小结构的位移响应，但TMD的吸振作用相对减少。同时，由图9可以看出，当结构的输入功率取峰值时，阻尼耗能功率和转移能功率也取得最大值，保证了结构安全性。

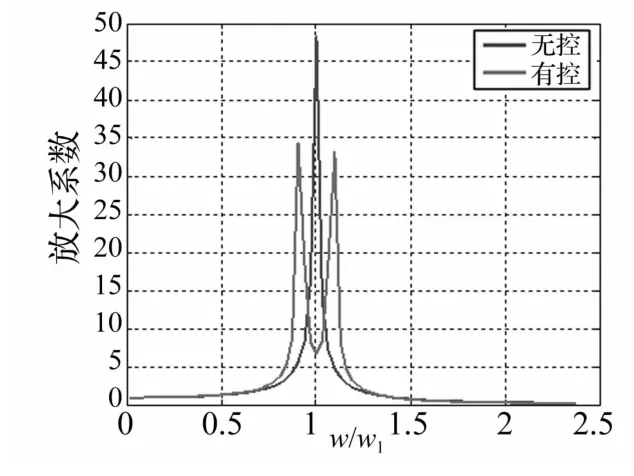
图6 TMD减振原理图Fig．6 Schematic of vibration reduction of TMD

图7 主结构耗能功率随周期的变化Fig．7 Dissipation power with structural period

图8 有控结构与无控结构的耗能功率比值Fig．8 Ratio of dissipation power between controlled and uncontrolled system

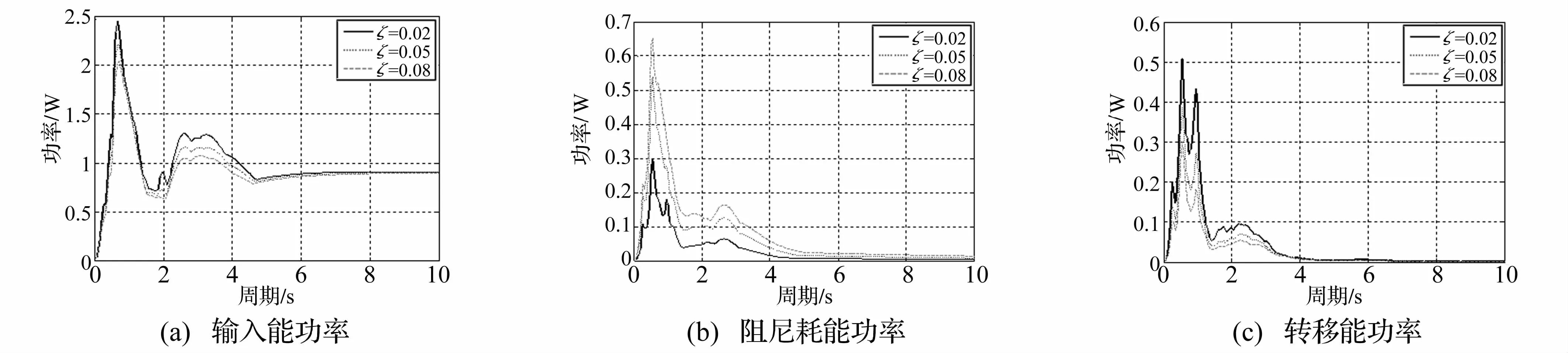
图9 主结构不同阻尼比下最大功率响应对比Fig．9 Maximum power response of main structure for various damping ratios

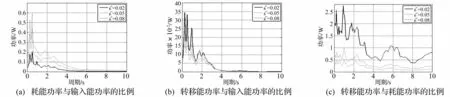
图10 相对值曲线Fig．10 Curves of the relative values

图10 给出了耗能功率、转移能功率及总输入能功率三者之间的相对值曲线。由图10（a）及10（b）可以看出，耗能功率与转移能功率占总输入能的比例随着主结构阻尼比的增大呈现截然相反的趋势，即主结构阻尼比越大，主结构的耗能越大，转移能越小。不同阻尼比情况下，转移能功率占主结构耗能功率的比例如图10（c）所示。主结构阻尼比较小时（ζ＝0．02），在地震波的主频附近，结构的转移能功率大于结构的耗能功率，其比值在1．5～2．5附近，而当远离地震波的主频时，结构耗能功率大于转移能功率。当主结构阻尼比ξ＝0．05、0．08时，转移能功率与耗能功率的比值均小于1，即主结构阻尼比越大，主结构自身阻尼耗能功率大于转移给TMD的功率，此时，主结构自身耗能是消耗地震能量的主要部分，TMD的贡献相对较小。

3 基于功率法的TMD参数优化

TMD参数的选取对TMD的控制效果有决定性的影响。Den Hartog［8］提出了不考虑主结构阻尼的TMD最优参数设计方法；Warburton［9］提出了用于单自由度无阻尼结构，在白噪声激励下，TMD的最优参数；Tsai等［10］推出了适用于有阻尼结构受基底激励时TMD的最优参数，Sadek等［11］提出了一种以结构－TMD系统前2阶模态阻尼比相等并且最大为目标，确定TMD最优频率比和阻尼比的方法。

结构的耗能功率体现了结构实时耗能的能力，因此，本文以主结构的耗能功率最小为优化目标得出TMD的最优频率比及阻尼比，并与上述四种优化方法做了对比分析。

3．1 主结构耗能功率公式推导

本节将考虑结构基底受到简谐激励＝P sin wt，通过待定系数法求解主结构的速度，从而得出主结构的耗能功率公式。

假设结构的稳态解为：

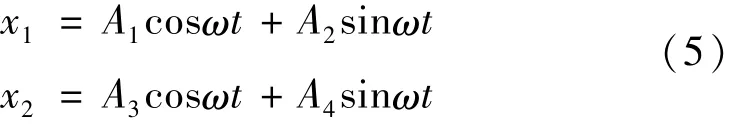
对应的速度与加速度为：

将式（5）、（6）代入到振动方程式（1）、（2）中并根据恒等式的条件求解四元一次方程组可得：

其中：主结构的频率 ω1，阻尼比 ξ1，TMD的频率 ω2，阻尼比ξ2，质量比为μ＝m2／m1。求解四元一次方程组得到 A1～A4，如式（7）所示。

主结构的速度：

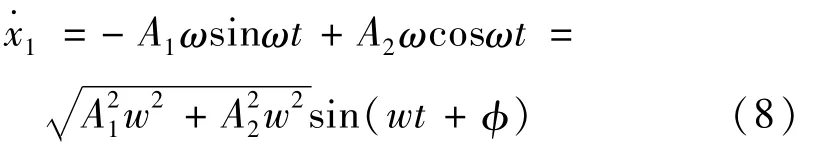
则主结构的耗能功率为：

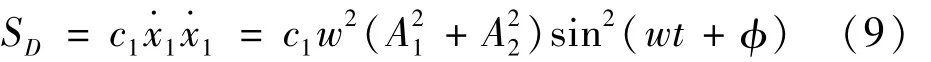
3．2 优化结果对比分析

以主结构的耗能功率最小为优化目标时得到TMD最优频率比及阻尼比，并与Den Hartog、Warburton、Tsai及Sadek提出的四种优化方法做了对比分析，对比图如图11所示。

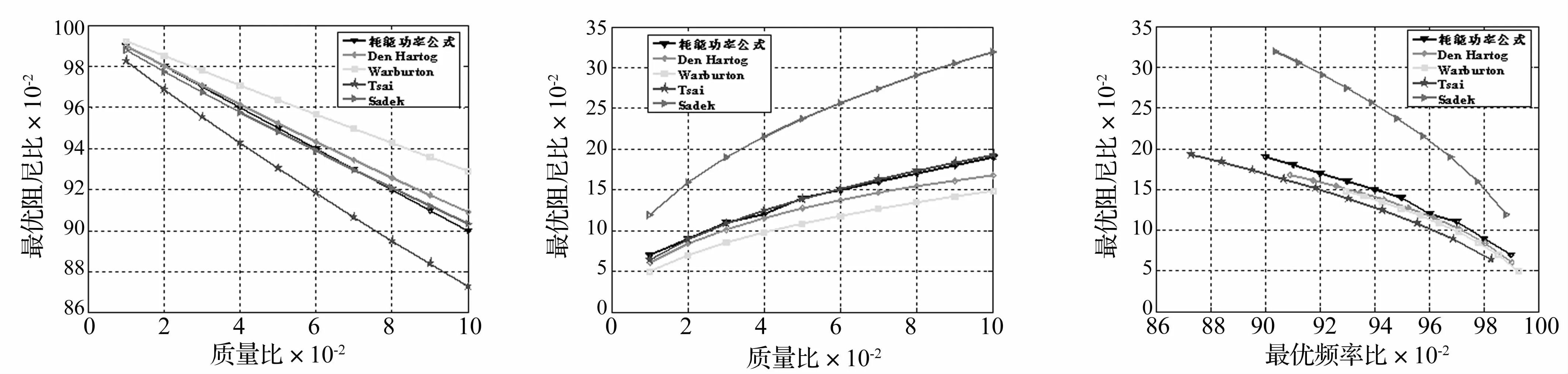
图11 质量比、最优频率比及最优阻尼三者之间的变化图Fig．11 Relationship among the mass ratio，optimal frequency ratio and optimal damping ratio

由图11可以看出，以主结构耗能功率最小为优化目标得到TMD的最优频率比及阻尼比的大小均介于上述四种优化方法之间。利用MATLAB中的公式拟合工具箱，可以得到基于主结构的耗能功率最小并考虑主结构阻尼比为0．02时TMD的最优参数公式为：

其残差分别为3．510 8e－16，0．006 080 3。

取质量比的变化范围为0．01～0．1，主结构的阻尼比为0．02，TMD的最优参数分别按上述五种方法选取，并假定地震激励的功率谱密度为白噪声S0，研究TMD系统在随机激励下的减振效果，结果如图12所示。

图12 位移方差对比Fig．12 Comparison of the displacement variance

由图12可以看出，基于主结构耗能功率优化的结构的位移方差较无控结构相比有很大程度的减小，且控制效果基本上介于 Den Hartog、Warburton、Tsai及Sadek提出的优化方法之间，因此该优化方法具有一定的适应性与可靠性。

3．3 优化后能量及功率对比

结构的基本参数与第二章节中采用的参数相同，下面取质量比为0．03，TMD的最优参数按上述五种方法选取，研究结构在EL Centro波作用下的能量和功率响应，并与无控结构做了对比。如图13所示。

由图13可以看出，当TMD的最优参数采用本文提出的优化方法时，结构的能量响应和功率响应与无控结构相比有一定程度减小，特别是主结构的阻尼耗能功率减小幅度明显，且控制效果基本上介于Den Har-tog、Warburton、Tsai及Sadek提出的优化方法之间。因此，本文提出的基于主结构耗能功率最小为优化目标的优化方法具有一定的可靠性且基于此方法得出的最优参数的公式对以后的研究具有参考价值。

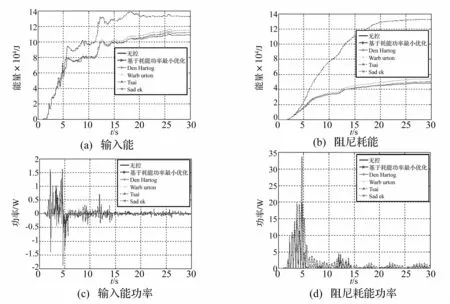
图13 结构能量及功率响应对比Fig．13 Comparison of structural energy and power history responses

4 结 论

（1）结构安装TMD后，结构的总输入功率、总弹性功率、总动能功率及主结构的耗能功率均有所减少，TMD系统对结构的响应有较好的控制效果。

（2）当结构自振频率与地震波的主要频率相近时，结构的各功率的峰值普遍较大。且TMD系统除了对于特别刚性的结构（T＜0．2 s）之外，都有减振效果。

（3）主结构的阻尼比对总输入功率峰值影响较小，对主结构的耗能功率峰值影响较大，且随着阻尼比的增大，结构的总输入功率减小，主结构的耗能功率增大，而TMD系统转移的功率随着阻尼比的增大而减小。随着主结构阻尼比的增大，主结构自身耗能成为消耗地震能量的主要部分，而TMD的贡献相对较小。

（4）以主结构耗能功率最小为优化目标得到TMD的最优频率比及阻尼比的大小均介于Den Hartog、War-burton、Tsai及Sadek提出的优化方法之间，且综合各项指标其控制效果均介于四者之间，但较无控结构相比有很好的控制效果。

［1］Soong T T，Dargush G F．Passive energy dissipation systems in structural engineering［M］．John Wiley＆Sons．Chichester，New Yark：1997．

［2］欧进萍，王永富．设置TMD、TLD控制系统的高层建筑风振分析与设计方法［J］．地震工程与工程振动，1994，14（2）：61－75．OU Jin-ping， WANG Yong-fu． Wind induced vibration analyses and design methods of tall buildings with tuned mass dampers or tuned liquid dampers ［J］． Earthquake Engineering and Engineering Vibration，1994，14（2）：61－75．

［3］李春祥，刘艳富．TMD－高层钢结构系统的风振舒适度控制设计方法［J］．振动与冲击，1999，18（2）：60－64．LI Chun-xiang，LIU Yan-fu．The design method regarding comfort control of wind-induced vibration for TMD-tall steel structure system［J］．Journal of Vibration and Shock，1999，18（2）：60－64．

［4］李创第，李暾，黄天立，等．高层建筑TMD风振控制分析的复模态法［J］．振动与冲击，2003，22（2）：1－8．LI Chuang-di，LI Tun，HUANG Tian-li，et al．Complex mode theory used for random wind＿induced response of structures with TMD［J］．Journal of Vibration and Shock，2003，22（2）：1－8．

［5］Housner G W．Limit design of structures to resist earthquake［C］／／Proc．1st World Conf．Earthquake Engineering，1956．

［6］谭平，潘兆东，王磊，等．基于能量原理的TMD系统减震性能分析［J］．桂林理工大学学报，2012，32（3）：123－235．TAN Ping，PAN Zhao-dong，WANG Lei，et al．Seismic performance of TMD system based on energy theory［J］．Guilin University of Technology，2012，32（3）：123－235．

［7］卜国雄，谭平，周福霖，等．基于能量法的TMD参数优化设计［J］．华中科技大学学报（城市科学版），2008，25（2）：26－30．BU Guo-xiong，TAN Ping，ZHOU Fu-lin，et al．Optimal parameters design of TMD based on energy method［J］．Huazhong University of Science and Technology，2008，25（2）：26－30．

［8］Den Hartog J P．Mechanical Vibrations［M］．4th ed．NY：McGrawHill，1956．

［9］Warburton G B．Optimum absorber parameters for various combinations of response and excitation parameters［J］．Earthquake Engineering and Structural Dynamics，1982，10（3）：381－401．

［10］Tsai H C，Lin G C．Optimum tuned mass dampers for minimizing steady state response of support excited and damped structures［ J］． Earthquake Engineering and Structural Dynamics1993，22（11）：957－973．

［11］ Sadek F，Mohraz B，Taylor AW，et al．A method of estimating the parameters of tuned mass dampers for seismic applications［J］．Earthquake Engineering and Structural Dynamics，1997，26（6）：617－635．

［12］田启强．地震动作用下结构能量反应研究及能量法应用初步［D］．北京：中国地震局工程力学研究所，2010．