超高层建筑多自由度气弹模型的优势及制作方法
王 磊,梁枢果,邹良浩,王述良
(武汉大学 土木建筑工程学院,武汉 430072)
风工程研究和工程项目抗风验算风洞试验方式通常有测力天平[1]、刚性模型测压[2]、强迫振动[3]、气动弹性模型[1,4-7]等,其中,气动弹性模型尤其是多自由度气弹模型被认为是最为精确的试验方式。一般来说,对于高度不太高或气弹效应不太明显的超高层建筑,通常采用刚性模型测压试验或测力天平试验进行抗风分析[2,8],而更为高柔的结构则常常要进行气弹模型试验,例如某菱形纪念碑[9]采用了摆式气弹模型(简称SDOF,下同)试验,金茂大厦[1]进行了多自由度气弹模型(简称MDOF,下同)试验。随着建筑高度的增加,气弹效应尤其是横风向气弹响应变得更为显著而复杂,气弹模型试验就更为必要。对多自由度气弹模型试验手段本身而言,既有相关研究还存在如下不足:一方面,对不同类型的模型试验结果对比分析不够全面,尤其对MDOF与SDOF两种气弹模型试验结果的差别没有给予足够的重视,Yoshie等[6]虽然初步提到,在相同的试验参数下,SDOF试验测得的横风向和扭转向风致响应比MDOF试验明显偏大,但未对其原因进行深入分析;另一方面,有关MDOF模型简化制作方法还有待进一步发展,Isyumov[10]、Yoshie等[6]、全涌等[11]、刘昊夫等[12]先后提出各自的制作方法,这些方法在弯曲振型和剪切振型所占成分控制、扭转向频率与平动频率的比例调节、高阶振型与低阶振型的比例关系和阻尼调节等问题上各有优势和局限性。基于上述分析,本文进行了同参数的MDOF与SDOF模型试验,分析了两模型风致响应出现显著差别的原因,并在此基础上提出了改进的MDOF模型设计方法。
1 不同试验方式对比分析
1.1 非气弹模型试验
刚性测压试验可以获得建筑表面的脉动风压时程,进而可根据结构动力学、随机振动理论及流体相似理论算得建筑物的极值风压和风致响应等结果。刚体模型测力天平试验可直接得到在来流紊流、结构尾流和特征紊流共同作用下脉动风荷载所引起的基底剪力和弯矩,即得到了建筑的一阶广义力,该试验方式直观简捷,但无法反应高阶振型的贡献。刚性模型测压试验和测力天平试验无法计及气弹效应的影响,尽管如此,对气弹效应不显著或不需考虑气弹效应的结构进行测压或天平试验可以满足工程或研究需要。
1.2 气弹模型试验
强迫振动试验是通过机械装置使上部刚性模型在流体中做定幅定频振动,通常是用来研究不同振动形式下模型表面的风压特性,该方式事实上考虑了流固互制作用,因而具有气弹模型的特点。强迫振动试验所得结果较为稳定,因而易于得到较为理想的内在规律,但强迫振动与建筑真实振动形式有所差别,所以该方式所得的气动参数结果具有一定局限性,其结果只可做为定性参考。
底部弹性支撑的摆式气弹模型试验模拟了结构的动力特性,可以直接测得包含气弹效应的表面风压和结构风致响应,但它只考虑了结构的一阶振型贡献,且模型沿高为线性振动,对于振型的差别可以通过振型修正来解决,但模型振动形式的简化所带来的气弹效应的差别却难以评估,从长期以来的试验经验来看,振动形式的微小差异就可能显著改变模型的气弹效应,进而造成风致响应结果相差悬殊(下文也说明了这一点)。MDOF模型试验则考虑了多阶振型的贡献,振动形式与实际情况比较一致,显然,MDOF模型在此方面是更具参考性的试验方式。
2 同参数下SDOF与MDOF试验结果比较
2.1 试验概况
图1显示了SDOF与MDOF模型的设计简图,模拟对象是高宽比为10的600 m方截面超高层建筑,几何缩尺比为1∶600,风速缩尺比为1∶6,频率缩尺比为100∶1,本文试验工况的模型一阶平动频率约为9.3 Hz,二阶平动频率约为27 Hz,在进行其他工况试验时该比值具有一定的可调性。测试内容为模型顶部横风向风致响应,试验风速为4~16 m/s,预计的横风向共振临界风速为9.5~10.5 m/s。试验风场的地面粗糙度类别有B类和D类流场,其湍流强度及风速剖面见图2。
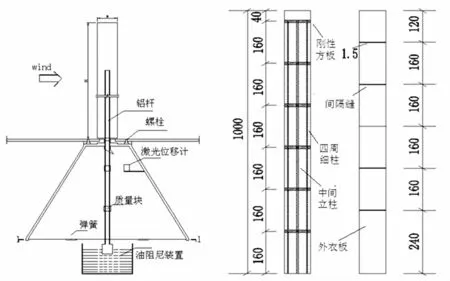
图1 单(多)自由度气弹模型设计简图Fig.1 Design of MDOF model and SDOF model
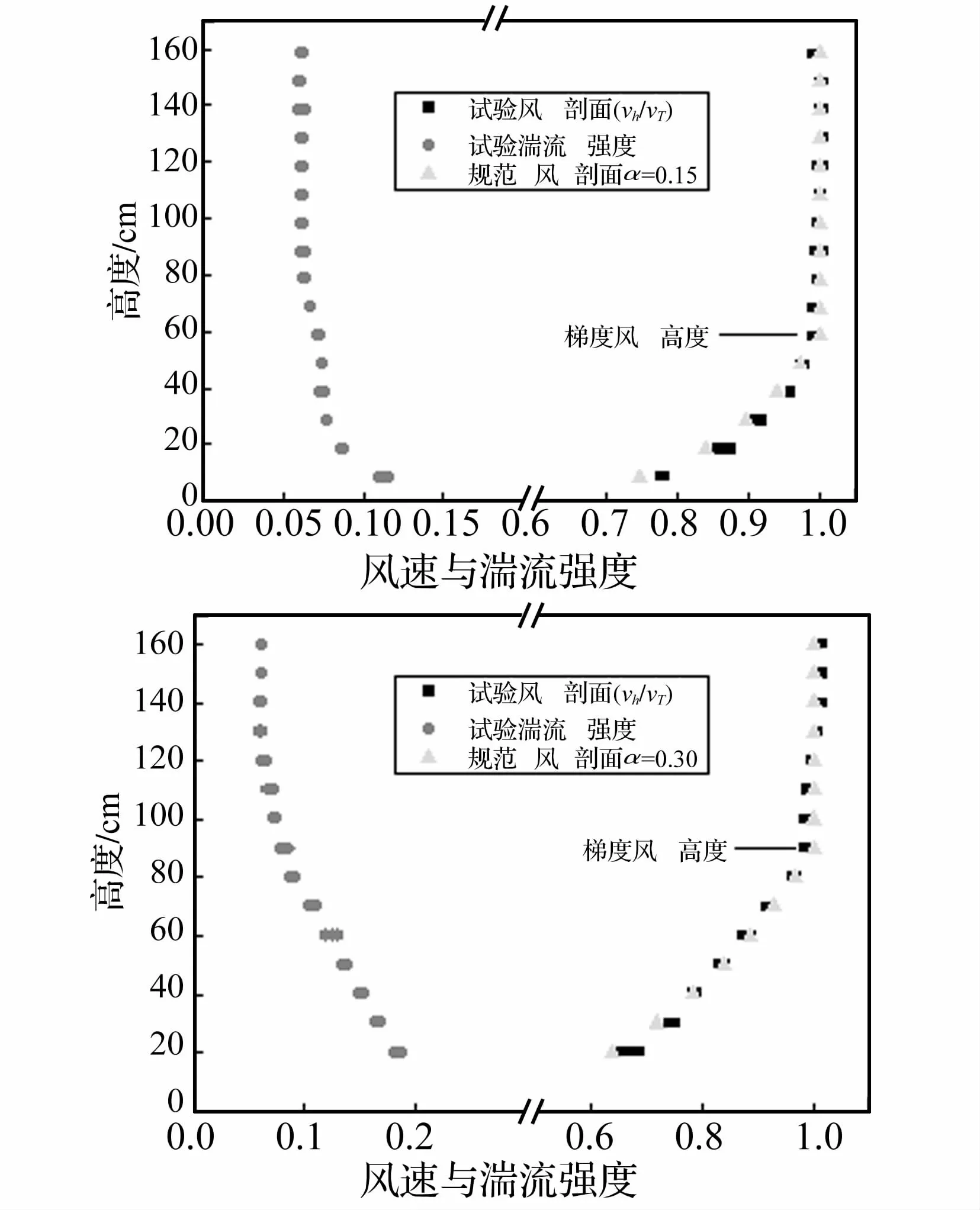
图2 B类风场和D类风场调试结果Fig.2 Wind velocity and turbulence intensity of exposure B and D
根据既有研究结论[13-14],横风向涡振位移随 Sc增大而减小,并在风场、模型尺寸等试验条件相同时与斯克拉顿数有确定的对应关系。基于这一规律,本次试验两模的型斯克拉顿数 (Sc=2Mξ/ρaD2)都设定为为2.50左右(其中 M,ξ,ρa,D分别表示模型当量质量、结构阻尼比、空气密度和模型宽度),以保证两模型试验结果的可比性,同时,两模型的当量质量、阻尼、频率也实现近似相等。
2.2 顶部位移比较
图3给出了同参数SDOF与MDOF模型在B类和D类流场中的顶部横风向均方根位移响应,图中V、n1,和D分别表示表示来流顶部风速、模型振动频率和模型迎风面宽度。从图3可以看出,SDOF与MDOF模型的横风向位移响应都随折算风速的增大而增加,并在折算风速为11附近达到最大,之后又逐渐减小,这一点与通常的结论是一致的[5,13],但SDOF模型测得结果比MDOF模型明显偏大,且最大值的相对差值甚至达到了100%。
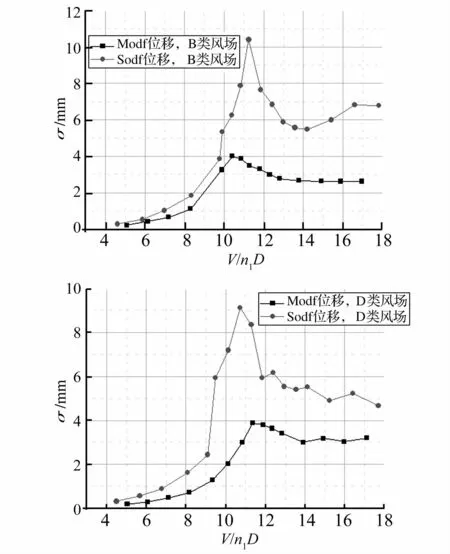
图3 SDOF与MDOF顶部横风向均方根位移响应Fig.3 Across-wind RMSdisplacement of two methods
图4 为Yoshie等[6]通过同参数SDOF与MDOF模型所得的横风向位移响应(其试验模型的模拟对象为400 m超高层建筑),可以看出,图4中SDOF模型位移比MDOF模型要大,尤其是对长边迎风的矩形截面柱体。对于本试验而言,由于模型相对较为高柔,两手段试验结果的上述差异也更为显著。为了探究两模型风致响应差异悬殊的原因,下文以B类风场的模型试验结果,从响应时程、响应谱、气动阻尼、气动刚度和表面风压等几个角度进行对比分析。
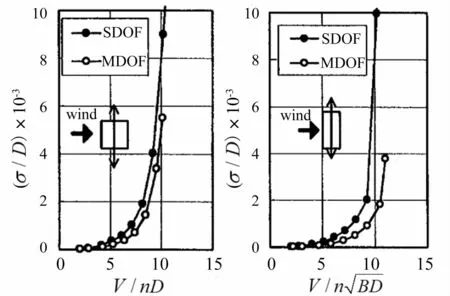
图4 Yoshie试验结果Fig.4 Test results by Yoshie
2.3 位移时程
图5 给出了两模型在共振风速下的顶部位移响应时程,从图5可以看出,SDOF位移整体值明显大于MDOF位移,且SDOF体系的振幅比MDOF更为稳定。通常认为,当发生锁定现象时,模型的横风向振动会从随机振动变为大幅简谐振动[15],且简谐振动振幅与均方根之比为1.41(此处暂且称其为峰因子),而新近研究发现,锁定时的振动位移曲线并不是严格的正弦曲线[16-17],只是定频变幅的类简谐振动,因而其峰因子并不是1.41。图6给出了两模型峰因子随折算风速的变化情况,可以看出,在小折算风速时两模型峰因子相当,而大折算风速时SDOF模型峰因子明显小于MDOF模型,这说明SDOF模型的振动形式更接近简谐振动,也使得SDOF模型的均方根位移更大。
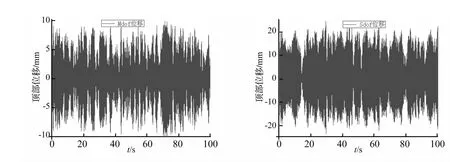
图5 MDOF与SDOF顶部位移响应时程Fig.5 Displacement time-history of two methods
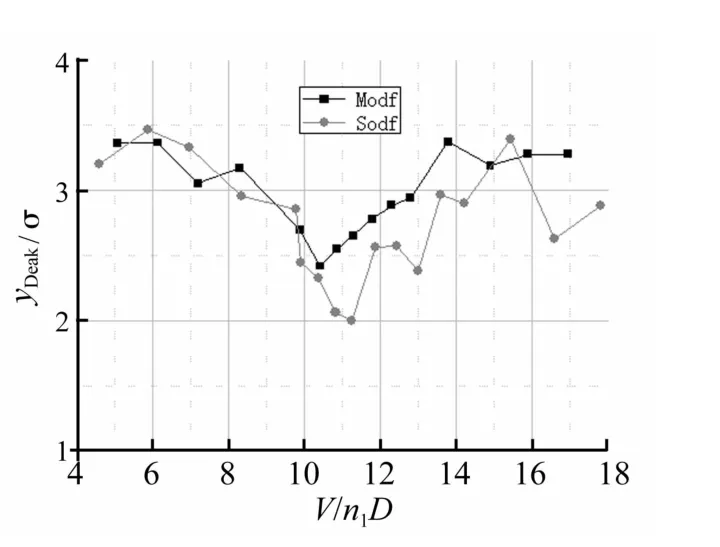
图6 峰因子随着算风速的变化Fig.6 Peak factor at different wind speed
2.4 位移响应谱与气动刚度分析
图7 为两模型在部分折算风速下的位移响应谱,从图7可以看出,小折算风速下的响应谱存在两个谱峰,分别对应于漩涡脱落频率和结构振动频率,在大折算风速下,两个谱峰“合二为一”并“停留”在结构振动频率附近。由于结构振动频率与气动劲度(主要为气动刚度)存在对应关系[3,5],从不同折算风速下的响应谱可以识别得到结构体系的振动频率,从而考察振动过程中气动刚度的变化。图8给出了不同折算风速下体系振动频率随折算风速的变化情况,从图8可以看出,SDOF体系的频率改变量较MDOF体系整体偏大,说明气动刚度对SDOF体系的影响相对较强。
2.5 气动阻尼分析
采用随机减量方法可以计算得到振动时的气动阻尼比,具体方法可参见文献[5]。图9显示了两模型在不同折算风速下的气动阻尼比,可以看出,气动阻尼比随折算风速经历了由正变负的过程,并且,在小折算风速时,SDOF体系的气动阻尼比绝对值大于MDOF体系,这对风致位移响应起抑制作用,而在大折算风速时则是相反的情况,此时的气动阻尼特性会加剧SDOF模型的风致位移,从而使两模型在大风下的风致响应差别更为显著。
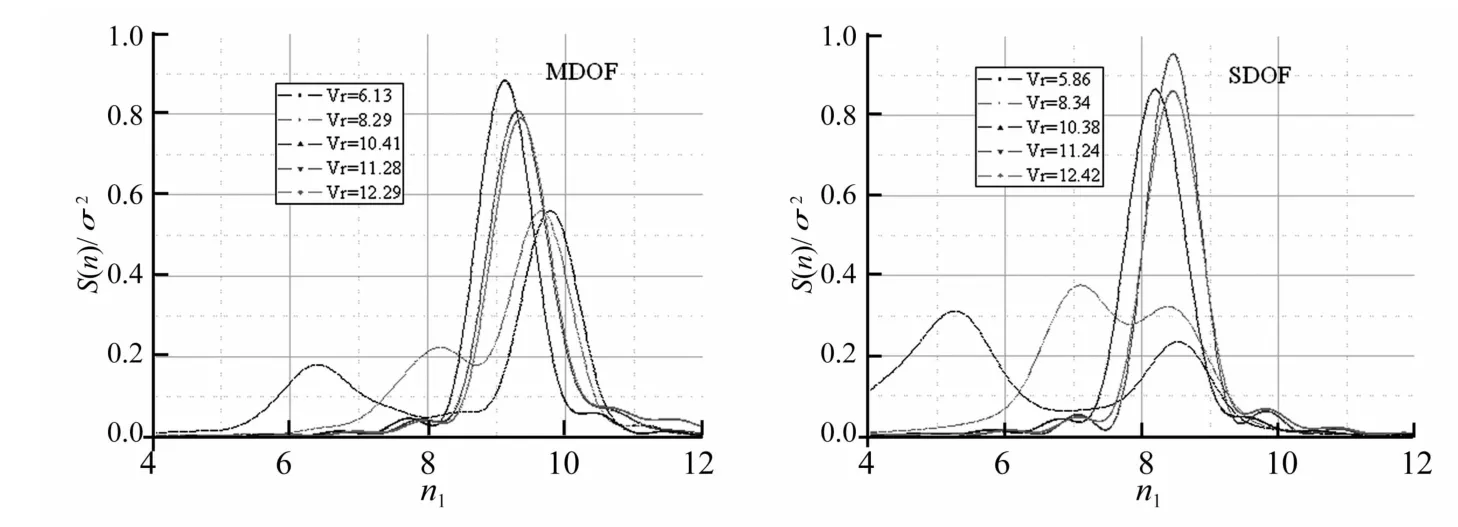
图7 MDOF与SDOF顶部位移响应功率谱Fig.7 Displacement spectrum of two methods
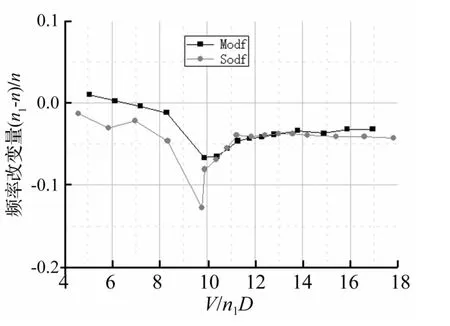
图8 频率改变量Fig.8 Frequency drift magnitude
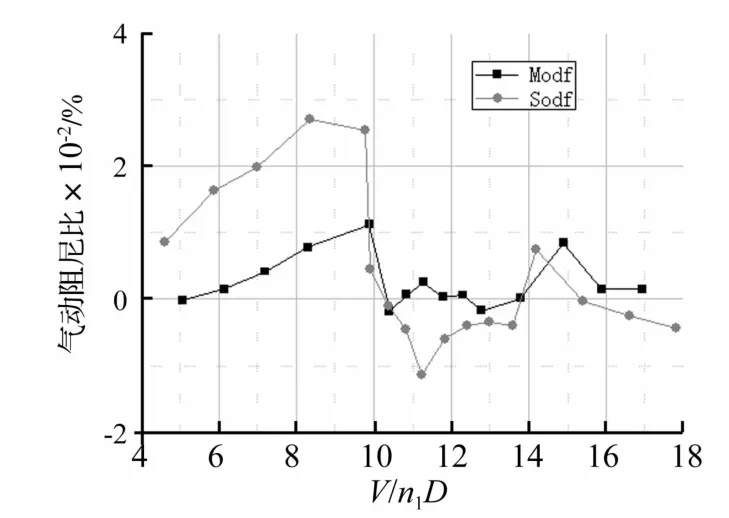
图9 气动阻尼比Fig.9 Aerodynamic damping
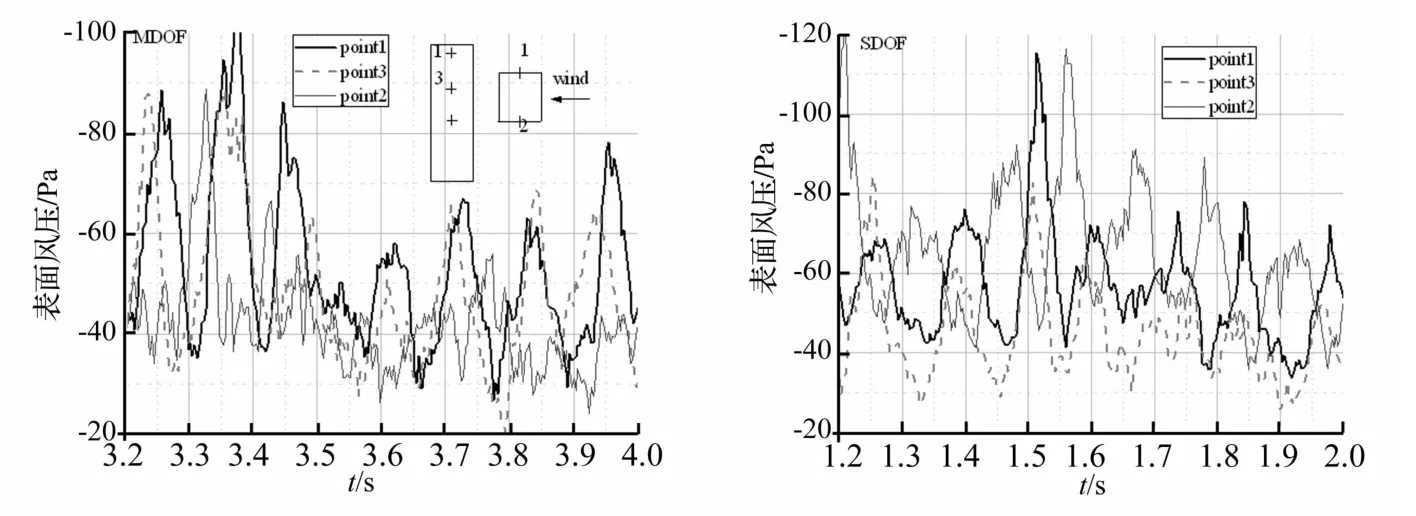
图10 MDOF与SDOF模型测点风压时程Fig.10 Time-history of point pressure
2.6 风压相干性分析
为了进一步分析两模型风致响应出现显著差别的原因,在模型表面布置了一定数量的测压点,用扫描阀同步测压,测压点布置及模型其他具体细节将在下一节给出描述。
同步风压时程见图10(此处只分析了几个典型测点,测点位置亦反映在图10中)。从图10可以看出,同一侧面上下两层测点的风压涨落趋势十分一致,即二者的风压相位近乎相同,同一层不同侧面测点间的风压涨落趋势大致相反,说明二者相位差近似为180°,并且,SDOF体系的这两种现象更为明显。
相干函数是直接描述两点脉动风荷载频域相关程度的参数,通常来说,相干函数随频率的增大呈迅速衰减趋势。但是,从图11的测点风压相干函数曲线可以看出,由于模型的大幅振动,相干函数都在振动频率附近显著增大,且SDOF同侧面不同高度的测点风压接近于完全正相干而,而不同侧面同一高度的测点接近于完全负相干,这种相位关系会加剧模型的风致响应,而MDOF测点的这种趋势相对较弱,这说明模型的振动形式对表面风压的相干性有较大影响,进而对风致响应产生影响。
2.7 原因归结
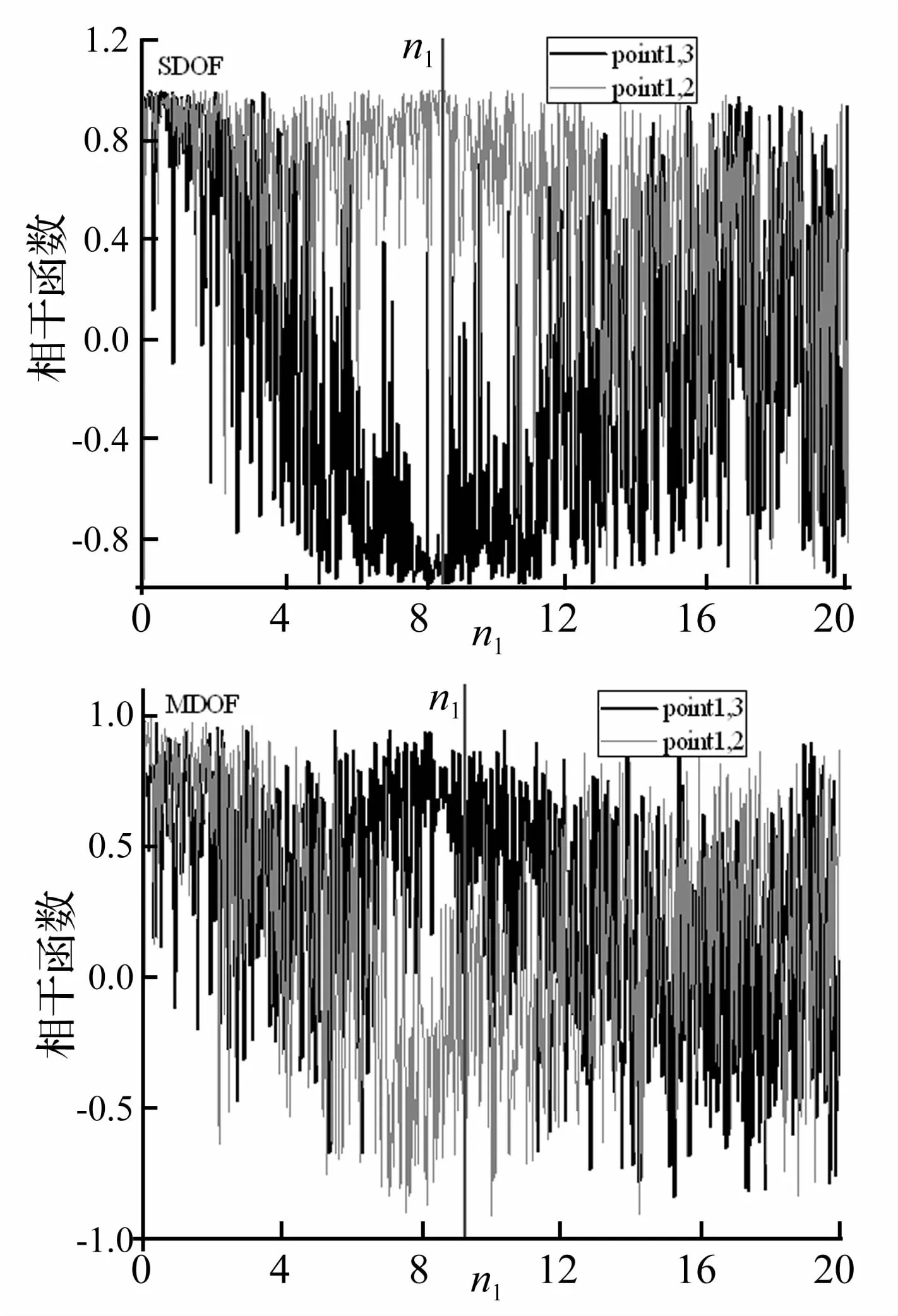
图11 MDOF与SDOF模型相干函数Fig.11 Coherence function of measuring points
事实上,从定性的角度来说,如果只考虑多自由度模型的一阶模态,并把多自由度模型的振型分为弯曲型、近似直线型和剪切型,则直线型多自由度模型的响应会与单自由模型一致,弯曲型情况的响应则大于单自由度模型,剪切型情况的响应会小于单自由度模型,但当考虑高阶模态时,尤其是高阶模态频率与基阶模态频率越接近时,这一定性规律则可能发生改变,因为高阶振型参振后会使振动形式发生改变,进而引起气弹效应在某种程度上的不同,并可能造成风致响应的显著差异。
2.2~2.6节的研究表明,只有一阶模态参振的SDOF模型与多阶模态参振的MDOF模型相比,不论是气动参数还是风荷载特征,都倾向于使SDOF模型会出现相对较大的风致响应。可见,参振模态差别并不仅仅造成和结构动力学理论对应的响应计算上的误差,而是振动形式的不同会很大程度引发流固互制效应的差别,进而造成风致响应的悬殊,换句话说,显著影响试验结果的不是参算模态(computing modes)而是参振模态(modes computing to vibrating form)。多自由度模型虽然能在很大程度上解决这一问题,但不同制作方式也会造成MDOF模型的各阶频率比等方面有所差别,这种差别对气弹效应及风致响应的影响难以评估,下文将对此进行针对性分析,同时考虑了弯剪振型成分控制和阻尼调节等问题。
3 多自由度模型改进设计方法
3.1 MDOF模型制作方法讨论
图12分别为文献[10-12]所采用的MDOF模型制作方法,这些方法各有优势与不足。具体来说:①采用中间一根立柱的方式较为简易,但会使扭转向刚度严重偏大,其振型成分主要为弯曲型,且不具有可调性;② 用弹性隔板的方式从理论来说可以考虑高阶振型的贡献和不同风向振型的耦合作用,尤其是可精确体调节扭转向振动特性,这种方式能够比较合理的模拟实际结构,但制作要求和难度较高;③ 采用四周可移动立柱的方式可调性较强,制作过程亦较为便捷,当立柱靠向中间时弯曲成分所占比例较大且扭转刚度和二阶平动频率相对提高(见图13,图中 d,L,fθ,f1,f2分别表示细柱间距、模型宽度、扭转频率、一阶平动频率、二阶平动频率),这种方式对高宽比不太大的建筑较为适用,而对更为高柔(如高度大于600 m)的结构则有其局限性,因为对于较高柔或高宽比较大的建筑,其λθ=fθ/f1通常较大,而 λ2=f2/f1则相对较小,例如天津高银 λθ为2.62,长沙J220的λθ和 λ2分别为2.08和2.23,所以四根立柱加方板的方式通常造成扭转频率较低而二阶平动频率较大。结合上节分析可知,在气弹模型制作时应尽可能地保证各阶频率与实际结构一致。
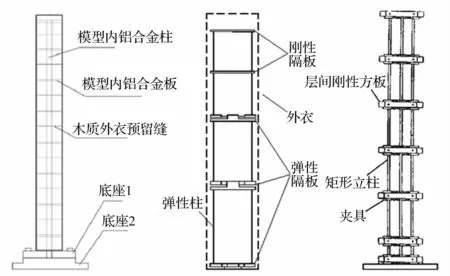
图12 MDOF模型既有制作方法Fig.12 Exist making method of MDOF model
3.2 MDOF模型改进制作方法
事实上,如果能将文献[10]和文献[11]的制作方法相结合,则在保留上述制作方法优势的同时又能很好地解决其不足之处,图14给出了相应的气弹模型改进设计简图,所模拟对象为高宽比为10的高层建筑。为满足铝板的刚度和质量要求,所加工的铝板为厚10 mm的异形铝板,该铝板在很大程度上借鉴了文献[11]的制作方法;在模型中心设置了一方形立柱,用以保证模型的整体稳定性、弯曲振型的特性和高阶振型与低阶振型的相对关系;四边有四根3~5 mm的方形柱可以左右(前后)移动以调节刚度,并控制偏心的具体位置;为控制方柱的移动精度及牢固动在刚性方板上设置了若干卡槽;刚性铝板上8个竖向备用螺孔可用于固定特制的质量块;对于通常来说较难实现的阻尼调节问题,采用了在模型内部加泡沫条的方法进行调节(见图15)。
按照上述设计方法建立有限元模型,图16显示了有限元软件计算的模型平动和扭转振型图。图17给出了几条自由振动曲线,可以看出,模型的振动模式是十分规则的衰减正弦曲线,并且,每条振动曲线代表了不同阻尼下的衰减曲线,说明上述调整阻尼的方法取得了很好的效果。
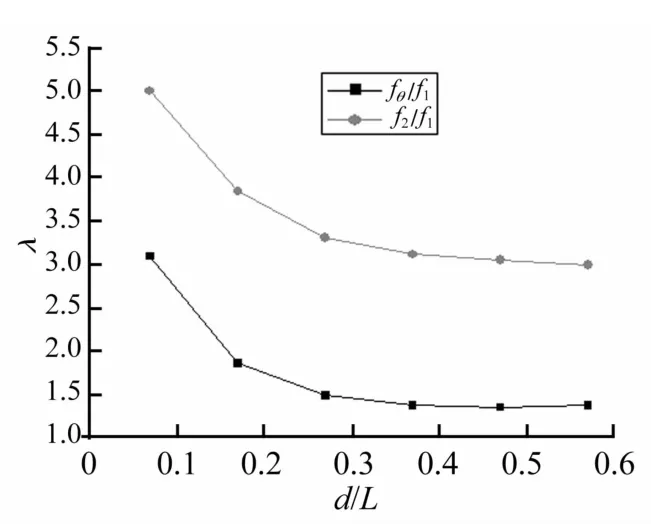
图13 细柱间距与频率比的关系Fig.13 Relationship betweenfrequency ratio and column distance
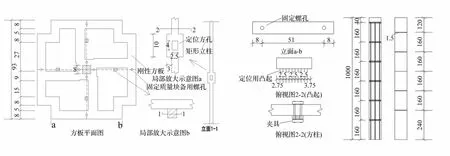
图14 气弹模型设计图Fig.14 Design of MDOF model

图15 气弹模型效果图Fig.15 Impression drawing

图16 模型振型图Fig.16 Mode shape
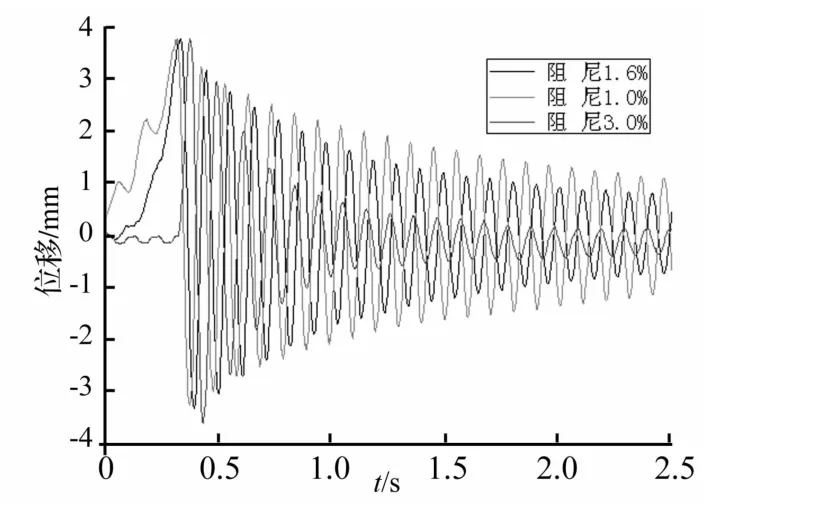
图17 模型自由振动衰减曲线Fig.17 Free vibration decay curve
4 结 论
本文讨论了气弹模型的优势及改进制作方法,结论如下:
(1)只模拟一阶模态的SDOF模型与实际振动形式不太吻合,与多阶模态参振的MDOF模型相比,这种偏差并不仅仅造成和结构动力学理论对应的响应计算上的误差,而是振动形式不同会很大程度造成流固互制效应的差别,进而引起风致响应的悬殊,即显著影响试验结果的不是参算模态而是参振模态。
(2)SDOF模型在发生涡致振动尤其是大幅涡振时的负气动刚度和负气动阻尼相对MDOF模型更为显著,SDOF模型所测的表面风压,在同一侧面不同高度测点之间近乎完全正相关,在两侧面对应位置测点之间则近乎完全负相关,而MDOF模型的此种现象则不太明显,这些特征都倾向于使SDOF模型会出现相对较大的风致响应。
(3)采用中间立柱、四周细柱加刚性方板的方法制作多自由度气弹模型,能够合理解决弯曲振型和剪切振型所占成分控制、扭转向频率与平动频率的比例调节、高阶振型与低阶振型的比例关系、阻尼调节和模型制作的便捷性等问题。
(4)对于较难实现的阻尼调节问题,采用在模型内部加泡沫条的方法可在保证结构刚度不变的同时较较好地调试出不同的阻尼。
[1]顾明,周印,张锋,等.用高频动态天平方法研究金茂大厦的动力风荷载和风振响应[J].建筑结构学报,2000,21(4):55-61.GU Ming,ZHOU Yin,ZHANG Feng,et al.Study on wind loads and wind-induced vibration of the Jinmao Building using high frequency force balance method[J].Journal of Building Structures,2000,21(4):55-61.
[2]梁枢果,邹良浩,郭必武.基于刚性模型测压风洞试验的武汉国际证券大厦三维风致响应分析[J].工程力学,2000,26(3):118-127.LIANG Shu-guo,ZOU Liang-hao,GUO Bi-wu.Investigation on wind-induced 3-D responses of Wuhan International Stock Building based on wind tunnel tests of rigid models[J].Engineering Mechanics,2009,26(3):118-127.
[3]Vickery B J,Stekley A.Aerodynamic damping and vortex excitation on an oscillating prism in turbulent shear flow.Journal of Wind Engineering and Industrial Aerodynamics,1993,49:121-140.
[4]曹会兰,全涌,顾明,等.独立矩形截面超高层建筑的顺风向气动阻尼风洞试验研究[J].振动与冲击,2012,31(5):122-127.CAO Hui-lan,QUAN Yong,GU Ming,et al.Along-wind aerodynamic damping of isolated rectangular high-rise buildings[J].Journal of Vibration and Shock,2012,31(5):122-127.
[5]吴海洋.矩形截面超高层建筑涡激振动风洞试验研究[D].武汉:武汉大学,2008.
[6]Yoshie R,Kawai H,Shimura M.A study on wind-induced vibration of super high rise building by multi-degree-of freedom model[J].Journal of Wind Engineering and Industrial Aerodynamics,1997,69-71:745-755.
[7]Fediw A A,Nakayama M,Cooper K R,et al.Wind tunnel study of an oscillating tall building[J].Journal of Wind Engineering and Industrial Aerodynamics,1995,57:49-60.
[8]邹良浩,梁枢果,汪大海,等.基于风洞试验的对称截面高层建筑三维等效静力风荷载研究[J].建筑结构学报,2012,31(11):27-35.ZOU Liang-hao,LIANG Shu-guo,WANG Da-hai,et al.Analysis of three dimensional equivalent static wind loads on symmetrical high-rise buildings based on wind tunnel tests[J].Journal of Building Structures,2012,31(11):27-35.
[9]宋微微,梁枢果,邹良浩.辛亥革命纪念碑风致响应的风洞试验研究[C].第八届风工程和工业空气动力学学术会议论文集,银川,2010:683-692.
[10]Isyumov N.The aeroelastic modelling of tall buildings[C].Proceedings of International Workshop on Wind Tunnel Modeling for Civil Engineering Application,Cambridge Universitu Press,1982.
[11]全涌,顾明,黄鹏.超高层建筑通用气动弹性模型设计[J].同济大学学报,2001,29(1):122-126.QUAN Yong,GU Ming,HUANG Peng.Design of super-high rise buildings’global aeroelastic model[J].Journal of TongJi University,2001,29(1):122-126.
[12]刘昊夫.典型高层建筑气动弹性的实验研究[D].汕头:汕头大学,2011.
[13] Allan L.A generalized model for assessment of vortex-induced vibrations of flexible structures[J].Journal of Wind Engineering and Industrial Aerodynamics.1995,57(2-3):281-294.
[14]梁枢果,吴海洋,陈政清.矩形超高层建筑涡激共振模型与响应研究[J].振动工程学报,2011,24(3):240-245.LIANG Shu-guo, WU Hai-yang, CHEN Zheng-qing.Investigation on model and responses of vortex-induced resonances of rectangular super high-rise buildings[J].Journal of Vibration Engineering,2011,24(3):240-245.
[15]Kwok K C S, Melbourne W H. Wind-induced lock-in excitation of tall structures[J],Journal of the Structural Division,1981,107(1):58-72.
[16]Cheng C M,Lu P C,Tsai M S.Acrosswind aerodynamic damping of isolated square-shaped building[J].Journal of Wind Engineering and Industrial Aerodynamics,2002,90:1743-1756.
[17]Melbourne W H.Predicting the cross-wind reponse of masts and strural members[J].Journal of Wind Engineering and Industrial Aerodynamics,1997,69-71:91-103.

