基于双层规划的交通疏散中车辆出发与交通控制综合优化

高明霞

（兰州交通大学交通运输学院,甘肃兰州 730070）

基于双层规划的交通疏散中车辆出发与交通控制综合优化

高明霞

（兰州交通大学交通运输学院,甘肃兰州 730070）

在有组织的区域性疏散中,从需求调节（即疏散车辆出发安排）和供给管理（即交通管控）两方面对疏散交通流进行合理组织,是提高疏散效率的有效途径。论文立足于疏散车辆出发组织与路网交通管控之间的双层决策关系,建立双层规划模型对集结点疏散车辆的发车频率、路线和交叉口控制参数进行综合优化,其中上层模型通过优化信号交叉口的相位绿灯时间即绿信比以降低平均延误,其决策影响到交叉口通行能力等供给特性；下层模型通过优化疏散车辆的分批出发时间与路线以压缩疏散总时间,其决策影响到交叉口流量等需求特性。设计了基于遗产算法的求解步骤,给出了一个数值算例。将模型优化方案和只从交叉口控制参数出发的单方面优化模式所得结果进行了比较,结果表明只从调整绿灯时间着手不结合车辆的出发组织,很难有效降低延误和压缩疏散时间。

交通疏散；出发安排；交通控制；综合优化；双层规划

1 引言

近年来,随着各种灾害性事件的不断升级,对应急管理提出了更高的要求。疏散是应急管理的重要内容,由于灾害的可预报性、事发地点的可预知性等各异,疏散管理的侧重点也有所不同。对事发地点、疏散范围相对明确的区域性疏散,国内外组织方式大体上可分为两种,一种是政府发布消息由居民自行决定出发时间和疏散方式等的无组织出发式疏散,另外一种是在指定的集结点由相关部门统一安排的有组织出发式疏散。我国家庭小汽车保有率低,交通疏散主要依赖公交车、单位车等方式,更适合有组织出发的疏散方式。对有组织疏散而言,疏散期间产生的交通流在很大程度上是可“组织”的,如果能够制定科学的疏散交通组织预案,干预疏散交通流在路网中的分布模式,使其向期望的良性方向发展,则能够大大提高疏散效率。

疏散交通流在路网中的分布情况,主要受疏散需求和供给特征两方面的影响,疏散交通组织也应从需求调节和供给管理两方面着手。就需求调节而言,总需求调节的弹性很小,而通过调节动态需求,如合理安排集结点疏散车辆的分批次出发时间或发车频率,可以避免交通流在短时间内突然加载到路网引发道路拥堵。在供给管理方面,道路网的几何特征在短时间内不易改变,而施加在其上的交通管控措施更具操作弹性见效也较快,所以适时改变路网中的交通管控措施,如优化交叉口的信号配时方案,可以对疏散交通流起到良性的干预和引导作用,缓解交通拥堵。

以往关于这类问题的研究,从需求调节（即疏散车辆出发安排）和供给管理（即交通管控）两个角度分别探讨的较多,但是将两者结合起来综合考虑的很少。Campos[1］提出了一种k-最短路方法寻求最佳疏散路线。Satoko等[2］采用动态最快流模型,对分批次车队的疏散路线和出发时间进行优化。Cova等[3］建立了一个基于车道的路口紧急疏导模型,通过人为干预车辆在路口的转弯,减少冲突、缩短疏散时间。Zhang Hailin等[4］将大面积疏散过程划分为步行至集结点和从集结点由交通工具疏散两个阶段,通过仿真对疏散车辆出发方案进行了比选。Wang Junwei等[5］研究了单源多汇情形下疏散道路的合理利用与修复问题。卢兆明等[6］建立了基于GIS和动态最快流模型的疏散管理系统框架,其中提出了综合车流出发安排与途中引导进行疏散交通组织的思路,但未有深入的量化结果。宋永朝等[7］运用最小费用最大流理论研究了局域路网中的疏散交通分配。

本文立足于疏散需求调节（即出发安排）和供给管理（即交通管控）之间的双层决策关系,建立双层规划模型对集结点疏散车辆的分批次出发时间、路线,以及路网中主要信号交叉口的控制参数进行综合优化,其中上层模型以疏散期间信号交叉口的车均延误（即平均每辆车的延误）最小为目标,对信号交叉口的相位绿信比（即有效绿灯时间与信号周期之比）进行优化,下层模型以总疏散时间（包括车辆在集结点的等待时间和途中的走行时间）最小为目标,对集结点疏散车辆的分批次出发时间、路线进行优化。对给定的上层决策,下层模型是一个动态系统最优的出发时间与疏散路线综合优化模型。设计了基于遗传算法的求解步骤,将其应用于一个小规模疏散路网,结果表明了该方法的有效性。

2 问题描述及模型

2.1 建模基础

由于疏散车辆出发安排和交叉口干预引导的主体及出发点不同,对疏散车辆的交通组织具有典型的双层决策特征,可将其描述为双层决策问题,其中决定交叉口管控方案的交管部门可看作上层决策者,而决定车辆出发时间及路线的组织方可看作下层决策者。上层决策者以充分发挥路网能力为目标,其决策直接影响着交叉口通行能力等供给特性,而下层决策者通常以缩短总疏散时间为目标,其决策决定着动态加载到路网的交通流及其空间分布等需求特性,上下层各自有其独立的决策空间,目标达成又都受对方的影响。

基于这一特征,建立双层规划模型,对集结点疏散车辆的分批次出发时间、路线和途中主要信号交叉口的相位绿信比（或绿灯时间）进行优化。为简便起见,对以下条件进行适当简化：

（1）所有信号交叉口都采用定时信号控制,信号周期固定,拟通过调节各相位绿灯时间来缩短疏散期间车辆经过交叉口的平均延误；

（2）各疏散集结点的总出行量已知,可根据集结点服务范围内的人口数及疏散车辆类型等综合确定,换算为标准当量小客车单位（pcu）；

（3）假定所有路段及交叉口的背景交通量为0,直接以路段、交叉口通行能力作为其疏散通行能力。区域性疏散不同于点对点式的救援疏散,其要求灾害影响范围内人群全部疏散,因此在疏散路网中,除了疏散初期存在部分背景交通流外,在疏散中后期主要包括自集结点产生的疏散交通流和调配空车产生的救援交通流,救援交通流与疏散交通流在占用同一道路时通常是相反方向且疏散期间的管制措施可以将两者有效分流,所以忽略两者影响；对疏散前期社会交通流的影响,可结合调查数据用路段通行能力等减去相应背景交通量,作为其疏散通行能力。

2.2 模型构造

将疏散路网抽象为有向网络G=｛V,A｝,其中V为节点集合,表示交叉口、疏散源点和疏散终点, A为弧集和,表示相邻节点之间的有向路段。设问题所在的时间段为[0,T］,并将[0,T］划分为K个大小为Δ的时段。另外为表述方便,定义以下符号和变量,其中下层模型中涉及变量如下：

R,S：道路网中疏散源点和终点的集合；r,s：疏散源点和终点,r∈R,s∈S；a：疏散路网中的路段,a∈A；n：疏散路网中的交叉口,n∈V；prs：源点r与终点s之间路径的集合；l：时段编号,表示车辆出发所在的时段,l=1,2,…,K；k：时段编号,表示车辆行驶在路网上的时刻所属时段,k=1,2,…, K；Drs：r、s之间总的疏散需求（车数）；：时段l内由r出发去往s且沿路径p走行的车辆数,p∈prs；F：的集合,∀r,s,p,l；xak：第k个时段的初始时刻行使在路段a上的车辆数；uak,vak：时段k内进入（离开）路段a的车辆数；,：时段l内由r出发去往s且沿路径p走行的车辆中,在时段k内进入（离开）路段a的车辆数；（F）：在F决定的交通状态下,在时段l内由r出发去往s且沿路径p走行的车辆花在路上的平均走行时间；A（n）,B（n）：以节点n为起点和终点的路段集合。：0-1变量,若时段l内由r出发去往s且沿路径p走行的车辆在时段k内进入路段a,则取1,否则取0。

上层模型中涉及的变量和符号如下：

I—信号控制交叉口个数；Ji—交叉口i的信号相位数；Ei—交叉口i的进口引道总数；y=（：i=1,2,…I；i=1,…Ji）为决策向量,其中表示交叉口i中相位i的绿信比（即该相位有效绿灯时间与周期之比）；ci—交叉口i的信号周期长（sec）；Li—交叉口i一个信号周期内的总损失时间（s）；—交叉口i的最小绿灯时间（s）；di—疏散期间交叉口i的车均延误（s）,即平均每辆车在该交叉口ii—0 -1变量,对于交叉口i,当进口道e在相位i的绿灯时间里允许通行时,δe经历的延误；qi-—疏散期间交叉口i的平均流率（pcu/s）,等于各进口道平均流率之和；—疏散期间交叉口i处进口道e的车均延误（s）；—疏散期间交叉口i处进口道e的平均流率（pcu/s）,等于疏散期间经过该进口道的总车数除以疏散时间；—0 -1变量,对于交叉口i,当进口道e在相位i的绿灯时间里允许通行时,=1,否则=0—交叉口i处,允许进口道e通行的绿灯时间在信号周期中所占的比例交叉口i处进口道e的饱和流量（pcu/h）；：交叉口i处进口道e的最大通过流率即通行能力（pcu/s）,由饱和流率和允许其通行的绿灯时长决定。

在上述前提下,疏散期间路网中信号交叉口的相位绿信比与疏散车辆组织方案的综合优化问题,可表示为以下双层规划模型：

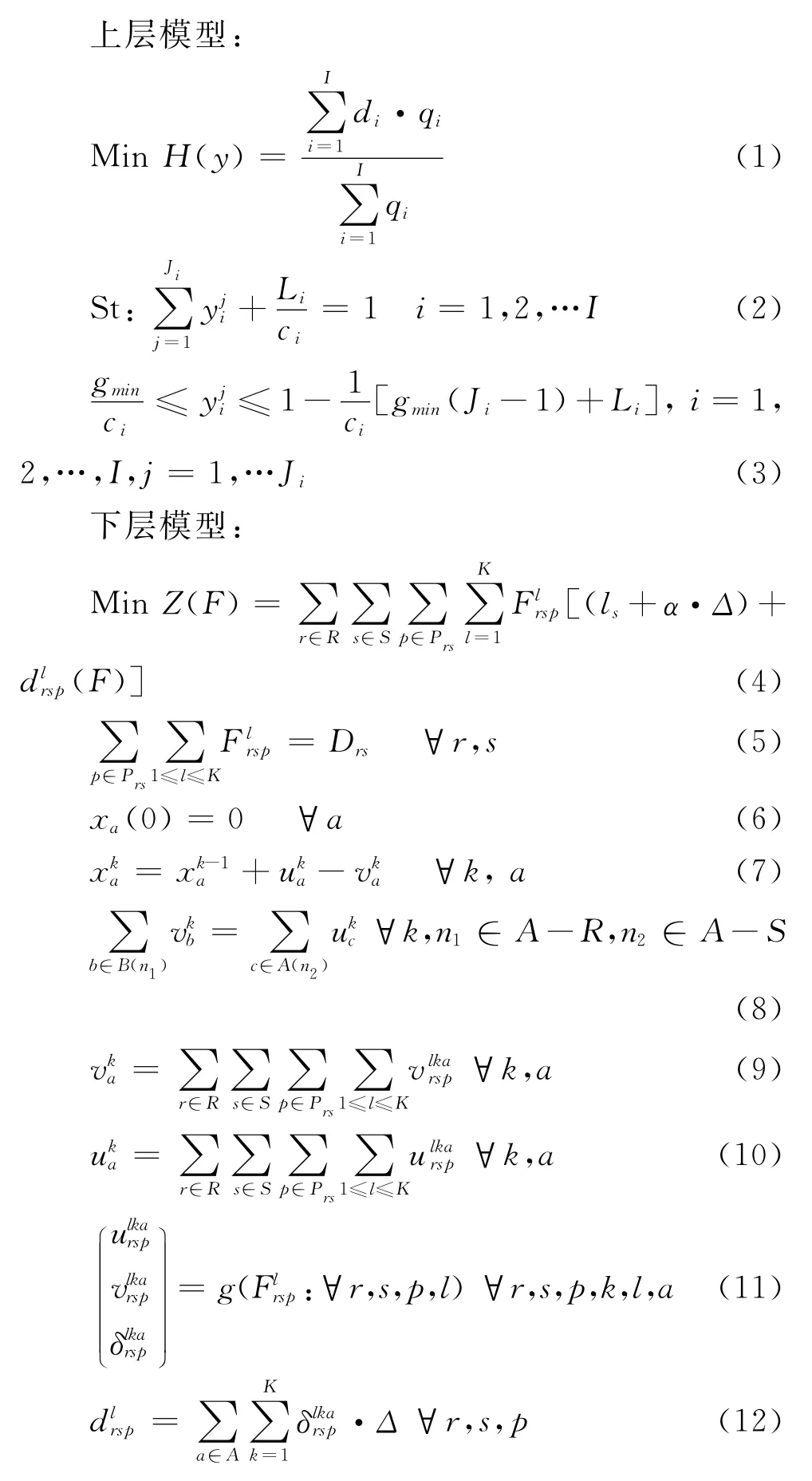
式（1）为上层模型的目标函数,表示上层目标为疏散期间所有信号交叉口的车均延误（即平均每辆车的延误）最小化,决策变量为信号交叉口的相位绿信比,其中di,qi可结合下层优化结果通过的下面的式子推算：

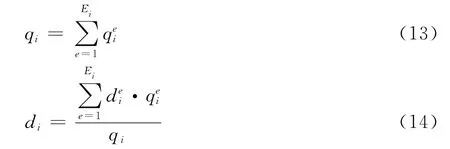
式（2）和式（3）是对信号交叉口相位绿信比的一般性约束；式（4）-（12）为下层模型,其目标是使包括车辆在疏散源点等待时间和途中走行时间的总疏散时间最小化,决策变量为疏散源点车辆的分批次出发时间和走行路线,对给定的上层决策,下层模型是一个动态系统最优的疏散路线与出发时间综合优化模型。对给定上层决策下,（4）-（11）所示下层模型的说明和求解,已在作者发表的其它论文中给出[9］,限于篇幅此处不再赘述。

2.3 模型的作用机制

模型可以对交叉口控制参数和疏散车辆的分批出发时间及路线同时进行优化,其作用机制如下：上层模型根据其目标确定决策变量y,即信号交叉口相位绿信比,该决策直接影响下层优化问题所依赖的路网条件,在此表现为各交叉口进口道的通行能力。对任意交叉口i,其进口道e的通行能力根据饱和流率模型由下式计算[8］：

下层模型在由上层决策决定的路网条件下,根据其目标确定决策变量F的取值,即各小时段内由疏散源点出发的车辆数及其路线,该决策直接影响和决定着疏散期间交通流在路网中的分布状态,包括交叉口进口道不同时刻的流率（t）和整个疏散期间的平均流率,这些流率取值直接关系到交叉口延误的大小,即上层目标的达成。下层决策的结果F通过流率反馈给上层,促使上层调整决策,改变y的取值。而y的改变造成了路网条件的变化,促使下层重新决策,这样反复循环,直至达到一个平衡,平衡状态下的解可认为是模型的最优解。

3 算法

3.1 算法步骤

上述双层规划模型中,下层模型本身是一个基于仿真的优化模型,而且上、下层决策变量之间的联系是隐含在描述疏散车辆走行的加载仿真模块中,无法给出其解析的表达,整个模型的解析性质较差。因此,采用遗传算法进行求解,算法主要步骤如下：

步骤1：确定编码方式、种群规模N、交叉概率pc和变异概率pm等参数；

步骤2：将式（1）所示的目标函数转换为适应度函数；

步骤3：初始化种群,产生N个可行的初始个体,即N个可行的y；

步骤4：计算个体的适应度

步骤4.1：将个体（解向量）y的值代入式（15）,得到下层模型中关于交叉口通行能力的约束；

步骤4.2：基于上层决策对应的路网条件,采用基于仿真的启发式算法求解下层模型；

步骤4.3：利用加载仿真模块,将下层模型的解所对应的车流加载到路网,得到交叉口各进口道的动态车流量qei（t）,∀i,e,t；

步骤4.4：根据式（1）、式（13）-（14））计算上层目标值H（y）；

步骤4.5：根据给定的适应度函数,计算个体适应度。

步骤5：根据适应度大小以一定的方式选择或复制个体；

步骤6：按交叉概率进行交叉操作；

步骤7：按变异概率进行变异操作；

步骤8：判断是否达到收敛条件,若已经达到则输出搜索结果,否则返回步骤4。

3.2 具体环节的实现

上述步骤中,步骤4.2和步骤4.3的实现,即给定上层决策下下层模型的求解已在作者发表的其它论文中介绍[9］。其他主要环节的具体实现分别说明如下：

（1）编码和解码

问题的可能解本身是连续变化的实数,所以采用实数编码,将解向量y直接表示为个体,解向量中的变量（yii）可看作是一个基因。这种方式下,求解过程不存在编码和解码操作,交叉、变异等遗传操作和解的评估、选择都是在同一个解空间中进行。

（2）设计适应度函数

此处的优化问题是个极小化问题,目标函数不能直接作为适应度函数,设计如下的适应度函数：

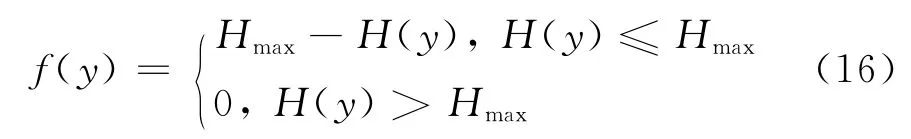
式中,Hmax为给定的足够大正数。

（3）遗传操作

此处采用轮盘赌的方式进行个体的选择；按一定交叉概率选择个体并分对,进行算术交叉；对以一定变异概率选中的个体y,采用单重均匀变异法进行变异,即按均匀分布随机选择个体中一个基因（变量）,并将它变异为其可行区间中的均匀随机数。

4 算例

图1所示为某城市局部疏散路网,其中节点1为疏散源点,节点9为该区域的疏散出口,其他节点代表交叉口,某些路段由于应急需要被规定为单向通行。

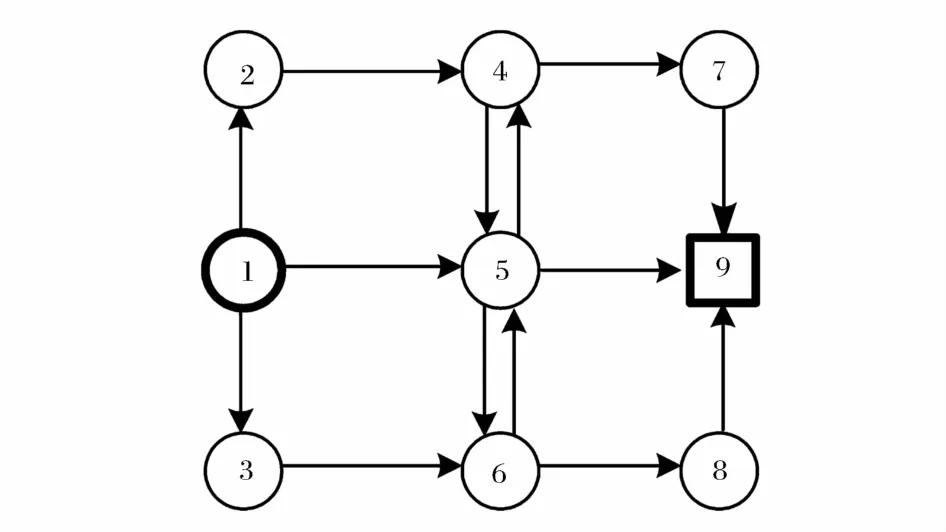
图1 算例中的疏散路网

假定疏散期间交叉口5、6均实行定时信号控制,其他交叉口则为无控交叉口。交叉口5、6的基本信息如表1所示,其信号相位方案分别如图2和图3所示。疏散路网中各路段的基本信息如表2所示,路网中无控交叉口各进口道的通行能力如表3所示。

令种群规模N=30,交叉概率pc=0.6,变异概率pm=0.06,最大迭代次数为400。假设疏散车辆数D1-9=1500（pcu）,采用上述模型对交叉口绿信比方案和车流出发组织方案进行综合优化,得绿信比方案及对应的延误如表4所示,与之对应的车流出发组织方案如表5所示。

另外,不难得到不考虑和车流出发组织的协调,只从上层目标—车均延误最小化出发,关于交叉口绿信比方案的优化结果。将下层模型的解固定,仍采用上面给出的遗传算法求解上层模型,其中取消步骤4.2,其他步骤保持不变,即可得到不考虑下层决策,只从上层目标出发的最优绿信比方案。本例中分别将疏散组织方案固定为前面综合优化过程中,编号为1至10的初始个体所对应的车流出发组织方案,依次按取消步骤4.2后的算法步骤求解上层模型,得到的优化结果如表6所示。

表1 信号控制交叉口的基本信息

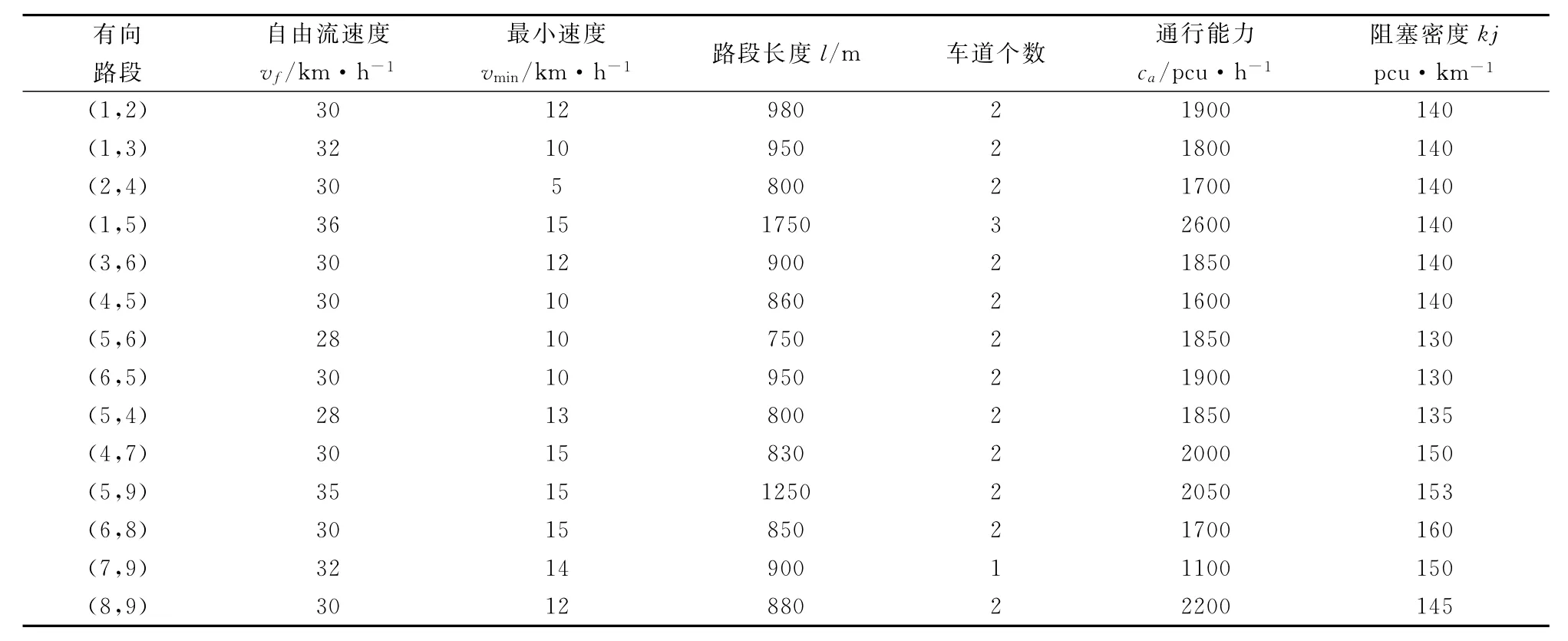
表2 路段的基本信息

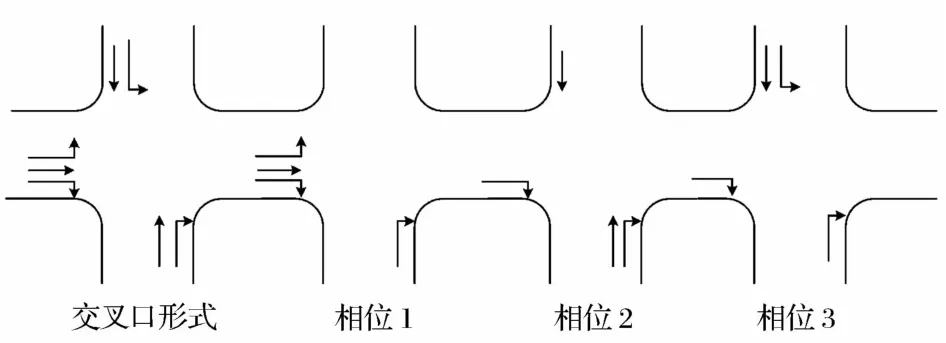
图2 交叉口5疏散相位方案

图3 交叉口6的疏散相位方案

表3 无控交叉口各进口道的通行能力

表4 基于双层规划的最优绿信比案及延误

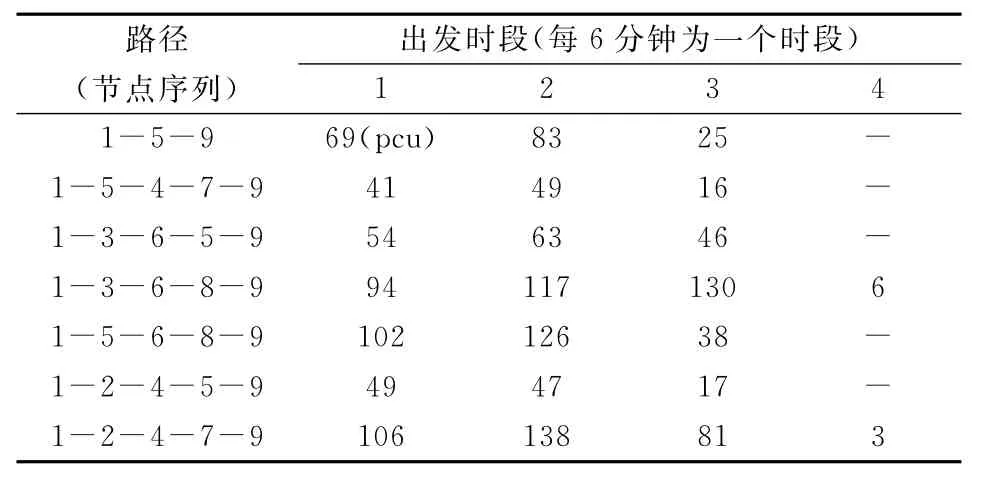
表5 基于双层规划的疏散车辆出发组织方案

从表4与表6中结果的对比情况可以看出,不结合疏散车辆的出发组织,只从上层目标出发单方面优化得到的绿信比方案,不但导致疏散时间明显增加,交叉口延误也没有得到有效降低。因为实际疏散中,交叉口延误不仅和绿信比有关,还取决于疏散期间通过交叉口的交通量。如果不结合疏散车辆的出发组织,不改变车流的出发模式,仅仅依靠绿信比的变化,很难有效降低延误、压缩疏散时间。

5 结语

区域交通疏散是应急管理的一项重要内容,科学合理的交通疏散预案对提高疏散效率具有重要作用。本文首先深入分析了疏散车辆出发组织和路网交通管控两者之间的双层决策关系,在此基础上建立了双层规划模型,对信号交叉口控制参数和集结点车队的分批次出发时间及路线进行综合优化,并跟据模型特点设计了基于遗传算法的求解步骤,最后通过一个算例说明了模型的应用,结果表明了该方法的有效性和较之单方面优化模式的优越性。

但是要真正服务于实际问题,还需要在大规模网络中结合实际数据进行进一步的实证研究。另外,如何将这些模型和算法与GIS等技术有效融合,开发真正能为疏散决策者所用的实用软件,也是下一步要研究的问题。

[1］Campos V B G,da Silva P A L,Netto P O B.Evacuation transportation planning：A method of identifying optimal independent routes[M］//Surcharov L J.Urban transport V：Urban transport and the environment for the 21st century.Southampton：WIT Press,2000：555-564.

[2］Satoko M,Kazuhisa M,Takashi T,et al.The Evacuation problem,dynamic network flows,and algorithms [C］.Proceedings of SICE Annual Conference,Fuku, Japan,August 4-6,2003.

[3］Cova T J,Johnson J P.A network flow model for lanebased evacuation routing[J］.Transportation Research Part A,2003,37（7）：579-604.

[4］Zhang Hailin,Liu Hao,Zhang Ke,et al.Modeling of evacuations to no-notice event by public transit system [C］.Proceedings of 13th International IEEE Annual Conference on Intelligent Transportation Systems,Madeira Island,Portugal,September 19-22,2010.

[5］Wang Junwei,Ip W H,Zhang Wenjun.An integrated road construction and resource planning approach to the evacuation of victims from single source to multiple destinations[J］.IEEE Transactions on Intelligent Transportation Systems,2010,11（2）：277-289.

[6］卢兆明,林鹏,黄河潮,基于GIS的都市应急疏散系统[J］.中国公共安全（学术版）,2005,1（2）：35-40.

[7］宋永朝,潘晓东,杨轸,等.灾害事件下局域路网应急疏散交通分配模型[J］.公路交通科技,2010,27（5）：88-92.

[8］王殿海.交通流理论[M］.北京：人民交通出版社,2002.

[9］高明霞,贺国光.动态系统最优的疏散路线与出发时间综合优化模型[J］.系统工程,2009,27（6）：73-77.

Optimization of Vehicle Departure Arrangement and Traffic Control in Traffic Evacuation Based on Bi-level Programming

GAO Ming-xia
（School of Traffic and Transportation,Lanzhou Jiaotong University,Lanzhou 730070,China）

It is an efficient method to manage traffic flow genarated in an organized regional evacuation from two aspects：demand regulation（means to regulate the departure mode of evacuation vehicles）and supply management（means to control traffic flow in road network）.Based on the bi-level decision relationship be-tween departure arrangement and traffic control in road network,a bi-level programming model is presented to optimize the departure plan and control parameters of intersections simultaneously.The green ratio of signalized intersections appears as the decision variable of upper level to minimize the average delay, which will influence some supply characteristics such as intersection capacity；the departure schedule and routes of evacuation vehicles appear as the decision variable of lower level to minimize the total evacuation time,which will affect some demand characteristics such as flow through intersections.A genetic-based algorithm is presented,and a numerical example is given.By comparing the optimization results of the bilevel model and the results got from the optimization mode that only consider the control parametar,it is shown that the bi-level model really holds advantage in decreasing delay and evacation time.

traffic evacuation；departure arrangement；traffic control；integrated optimization；bi-level programming

U491；O157.6

A

1003-207（2014）12-0065-07

2012-03-15；

2013-05-15

教育部博士点基金资助项目（20116204120005）；教育部人文社科基金项目（12XJCZH002）；兰州交通大学青年基金

高明霞（1979-）,女（汉族）,宁夏中卫人,兰州交通大学交通运输学院副教授,博士,研究方向：交通系统工程.