基于LTCC技术的椭圆函数低通滤波器设计
秦 舒
(华进半导体封装先导研发中心有限公司,江苏 无锡 214135)
1 引 言
滤波器的主要功能就是滤除通带外的干扰信号,使需要频段内的信号得到良好的传输[1~4]。对低通滤波器来说,在截止频率外是否能达到陡峭的高抑制衰减是衡量滤波器性能的一个重要指标[5,6]。
图1给出了Ansoft Designer对巴特沃滋(Butterworth)低通滤波器、切比雪夫(Chebyshev)低通滤波器以及椭圆函数(Elliptic)低通滤波器在相同阶数、相同截止频率条件下的S参数电路仿真结果,从图中可以看出三类滤波器不同的衰减特性。
椭圆函数低通滤波器通带到阻带的截止率最陡峭,在截止频率外通过很窄的过渡带就能达到很高的衰减,并且在阻带中有传输零点;切比雪夫低通滤波器的衰减率在椭圆函数低通滤波器和巴特沃斯低通滤波器之间;巴特沃滋低通滤波器在通带内有着较好的纹波,但衰减率不甚理想[7]。巴特沃滋低通滤波器和切比雪夫低通滤波器类似,其所有传输零点都位于无限远处。在微波通信领域,往往需要一定频带内的陡峭衰减[4],椭圆函数滤波器通带到阻带优良的过渡特性无疑是最佳选择。

图1 不同响应的衰减特性对比
图2给出了椭圆函数低通滤波器在阶数n不同的情况下的传输特性曲线,三阶的椭圆函数低通滤波器在阻带形成了2个传输零点,带外衰减率最低;七阶的椭圆函数低通滤波器在阻带中形成了3个传输零点,衰减特性居中;九阶的椭圆函数低通滤波器在阻带中形成了4个传输零点,截止频率处衰减率最高,阻带中的抑制度也最高。
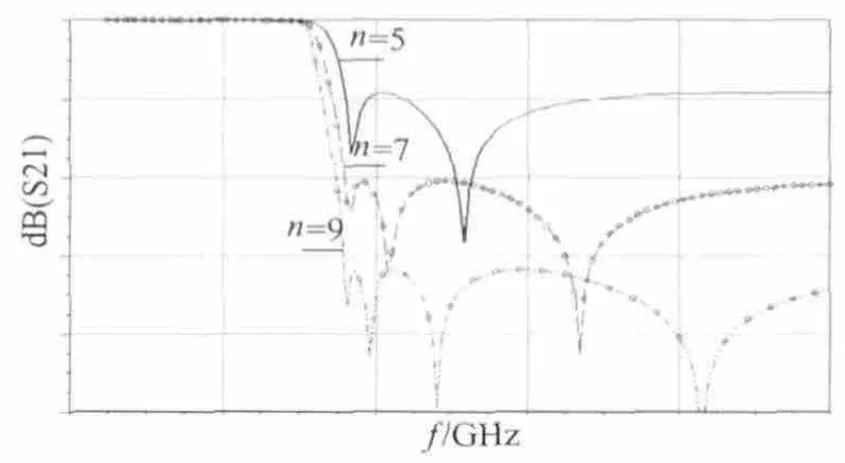
图2 不同阶数椭圆低通滤波器传输特性
可以看出,随着椭圆函数低通滤波器阶数的增加,阻带中的传输零点会随之增加;在阻带中增加传输零点个数,通带外的衰减率会随之提高,阻带的抑制度也会加大。因此,在设计滤波器时,要使在截止频率处的衰减率加大,阻带中实现高抑制度,可通过增加滤波器阶数来满足。在本文中将利用LTCC技术,同时考虑电路的性能和面积问题,利用三维高频仿真软件HFSS设计一款高性能小型化椭圆函数七阶低通滤波器。具体要求如下:3 dB处截止频率1.35 GHz,在1.65 GHz处的衰减达到-40 dB,同时要求很好的高次谐波抑制和阻带衰减特性。表1为此款滤波器的设计指标。

表1 滤波器的设计指标
2 滤波器设计
如图3所示,椭圆函数七阶低通滤波器的电路包括串联支路中的4个电感和并联支路中的3个LC谐振腔。这3个LC谐振腔可以在阻带中引入3个传输零点。每一个传输零点发生在特定的谐振频率处,此处电路的Q值为零,信号将会被全反射。

图3 椭圆函数七阶低通滤波器电路原理图
在设计时,可以调整谐振腔中电感、电容值的大小,使每一个LC谐振腔产生的传输零点按顺序排列。如图4所示,使中间的LC谐振腔产生第一个传输零点,左边的LC谐振腔产生第二个传输零点,右边的LC谐振腔产生第三个传输零点。

图4 电容设计示意图
在本文中,金属导线材料选用银,导线厚度为10 μm,LTCC材料的介电常数为7.8,损耗角正切值为0.002。此款滤波器将被设计为19层,模型最上边4层和最下边4层为薄层,LC谐振腔中的3个电容会被放置这些层中,7个电感将放置在另外11个厚层中,这样就会形成上下电容、中间电感的结构。模型的尺寸为:3.2 mm×2.0 mm×1.4 mm。滤波器的结构布局由表2、图5可以看出。
如图6所示,滤波器放置在PCB基板上进行仿真测试,滤波器输入输出端口通过金属引线与PCB板连接。
这里选用的PCB基板材料为Rogers RO4350,介电常数为3.48,基板高度设计为0.508 mm,导线宽度为1.13 mm。这样通过式(2)和式(3)便可使输入输出端口的阻抗分别为50 Ω。图7为滤波器的S参数测试结果。

表2 滤波器的结构布局

图5 滤波器3D结构图

图6 滤波器3D外观图
由图7可以看出,S21曲线在3 GHz以内的阻带中没有达到-40 dB的衰减,电路在4.5 GHz左右发生谐振,产生了尖峰,S11在通带范围内大于-10 dB,使VSWR大于2。测试结果没有满足设计指标要求。

图7 S参数测试结果
出现这种问题的原因有以下两点:
(1)模型内部元件之间的相互寄生耦合
由于要在3.2 mm×2.0 mm的有限长宽范围内实现10个元件的物理结构布局,元件和元件之间的相互耦合作用是必然存在的。由于模型内部结构紧凑,元件与元件之间的距离较小,元件之间难以避免的寄生效应导致了模型测试结果与预期结果产生了偏差。
(2)实现电感过程中造成的误差
在这款滤波器设计中,电感模型采用平面螺旋电感结构,由于电感面积较大,很容易和垂直相邻的上、下层中的元件发生寄生效应,并且电感离地层高度的不同会造成电感值的很大偏差。
通过分析,找出了问题的所在,那么如何减小模型内部的寄生耦合效应、调整电感的设计是接下来要做的工作。
3 滤波器优化设计
如图8、图9所示,在平面螺旋电感元件的布局方面,每一个LC谐振腔中的电感C都与串联支路中相邻的两个电感A和B垂直放置,电感C在中间层,电感A和B分别在其上、下的相邻层,而层距只有86.9 μm,这样的结构使得相邻层的电感走线间产生了寄生电容,且相邻的电感间又发生了紧耦合效应,使电感值产生了偏差,导致滤波器模型的仿真结果与预期结果产生差异。

图8 电感耦合示意图

图9 螺旋电感耦合示意图

图10 调整后的螺旋电感示意图
为了避免这种寄生耦合现象,设计时可以改变螺旋电感的内径、调整圈数,在保证电感值大小尽量不变的前提下,使上、下相邻层的电感在垂直方向的投影减少重合,从而减小了相邻层电感之间的寄生耦合。图10为调整后的螺旋电感示意图。在相邻层的电感布局结构调整后,模型的仿真曲线如图11所示。

图11 结构优化后的S参数测试结果
可以看出,在对电感做了调整之后,模型的仿真结果得到了改善,仿真结果可以满足表1中提出的指标。
图12给出了滤波器在结构优化前后的仿真结果对比,结构优化后的测试结果相对于结构优化前在以下方面得到了改善:
(1)通带中回波损耗从-7.6 dB下降到-11.5 dB;
(2)阻带中引入了4个传输零点,得到了理想的衰减效果;
(3)在阻带中1.61~3.10 GHz的频带内,滤波器具有大于40 dB的抑制;
(4)在阻带中3.10~6 GHz的频带内,滤波器具有大于30 dB的远端抑制。

图12 结构优化前后的S参数对比结果
结构优化后的滤波器性能可以满足提出的设计指标。通带内插入损耗和回波损耗分别是-0.6 dB和-11.5 dB,截止频率在1.35 GHz处;在截止频率外滤波器通过260 MHz的过渡带达到了-40 dB的衰减;1.61~3.10 GHz的频带内抑制大于40 dB;3个零点分别在f1=1.65 GHz、f2=1.85 GHz、f3=2.60 GHz处获得,在4.6 GHz处又产生了第四个零点,使得衰减效果更为理想。基于LTCC技术设计的此款椭圆函数七阶低通滤波器通过对内部结构的优化,成功地避免了寄生效应的产生,使滤波器达到了高性能的指标要求。
4 结论
本文阐述了结合引入传输零点的规律和方法,设计了含有3个LC谐振腔的椭圆函数低通滤波器等效电路,每个LC谐振腔在其谐振频率处可以引入一个传输零点。建立好的等效电路包括串联支路中的4个电感和并联支路中的3个LC谐振腔,共10个元件。为了充分发挥LTCC技术的三维空间优势,缩小器件体积,滤波器模型的物理结构设计为19层,体积为3.2 mm×2.0 mm×1.4 mm。
通过对滤波器模型内部物理结构的优化,避免了滤波器元件间的寄生耦合效应,使滤波器的性能得到了改善,其特性可以满足高性能应用指标的需求。测试结果为:通带内插入损耗和回波损耗分别是-0.6 dB和-11.5 dB,截止频率为1.35 GHz,通带外的截止率陡峭,阻带中引入的4个传输零点使滤波器的衰减效果更为理想。
[1]邓重.滤波器的过去、现在与未来[J].今日电子,2005,4(7): 48-50.
[2]Inder Bahl,Prakash Bhartia.微波固态电路设计[M].北京:电子工业出版社,2006.
[3]甘本胈,吴万春.现代微波滤波器的结构与设计[M].北京:科学出版社,1973.
[4]Kai Chang.Encyclopedia of RF and Microwave Engineering[J].ISBN: 978-0-471-27053-9,March 2005.
[5]David M Pozar.微波工程[M].北京:电子工业出版社,2008.
[6]ASOD A,ALSEYAB.A Novel Class of Generalized Chebyshev Low-Pass Prototype for Suspended Substrate Stripline Filters [J].IEEE Trans.Microwave Theory and Techniques,1982,MTT-30: 13416-1347.
[7]Milosavljevic Z D.Design of generalized Chebyshev filters with asymmetrically located transmission zeros [J].IEEE Trans.Microwave Theory Tech.,2005,53: 2411-2415.

