三视图向直观图转化时存在的障碍与突破方法

●余继光 (柯桥中学 浙江绍兴 312030) ●陈朝阳 (余杭区教育局教研室 浙江杭州 311100)

三视图向直观图转化时存在的障碍与突破方法

●余继光 (柯桥中学 浙江绍兴 312030) ●陈朝阳 (余杭区教育局教研室 浙江杭州 311100)

有关三视图的试题最常见的是给出正视图、俯视图、侧视图后计算几何体的体积，然而在由三视图画直观图或想象空间几何体的形状过程中，由于空间概念弱或逻辑推理不当，学生常会遇到思维障碍，突破这一障碍就需要寻找或掌握此类问题的思维规律，抓住平行投影的特点，以及斜高的特定位置，从而驾驭此类问题.

1 平行投影描绘几何体的点、线、面

三视图是在平行投影下对几何体从三维向二维的转化，由于要对几何体从3个不同的方向进行投影，因此就会有3个可变化的情形或变量，认识它时就必须全面而准确，关键是在平行光线下寻找到其投影.

图1

例1如图1，E，F分别是正方体的面 ADD1A1，BCC1B1的中心，则四边形BFD1E在该正方体面上的射影可能是 (如图2所示，要求把可能的图的序号都填上).

图2

障碍点(1)不按平行投影规则来看几何体而导致出错;(2)没完成3个方向上的平行投影而导致出错.

突破口由三视图的定义研究四边形BFD1E在该正方体面上的射影可分为：上下、左右、前后3个方向.由于线是由点确定的，故研究四边形的4个顶点在3个投影面上的射影，再将其联结即可得到3个视图的形状.因为正方体是对称的几何体，所以四边形BFD1E在该正方体面上的射影可分为：上下、左右、前后3个方向，也就是在面ABCD，ABB1A1，ADD1A1上的射影.

四边形BFD1E在面ABCD和面ABB1A1上的射影相同，如图2②所示;四边形BFD1E在该正方体对角面的ABC1D1内，它在面ADD1A1上的射影显然是一条线段，如图2③所示.故②③正确.

简单空间图形的三视图，主要考查根据作三视图的规则来作出3个视图的能力.三视图的投影规则是：主视图与俯视图要长对正;主视图与左视图要高平齐;左视图与俯视图要宽相等.

2 几何体中斜高在三视图中位置

例2 若某几何体的三视图(单位：cm)如图3所示，则此几何体的表面积为 .

图3

(2013年浙江省数学高考试题改编)

障碍点(1)此三视图对应的直观图与实物是什么;(2)计算表面积时，侧面图形是什么.如果是三角形，计算三角形面积时，三角形的高是直观图中的斜高还是其他，在三视图中有此线吗?

突破口根据三视图先画出三棱柱的底面，然后画出三棱柱，再寻找点F的位置.可见几何体是一个直三棱柱截取一个直角四面体后的空间图形(如图4所示)，它的5个面分别是正方形、梯形、三角形，其面积分别为：

图4

此题在准确画出直观图后，关键是判断△DEF的形状与大小，以便于找到三角形的高(此高在三视图中任何线段都不能表达)，从而准确计算其面积.

例3若某几何体的三视图(单位：cm)如图5所示，则该几何体的体积为 ( )

图5

A.10 cm3B.20 cm3C.30 cm3D.40 cm3

障碍点根据三视图有的学生判断此几何体为以俯视图为底的三棱锥，于是计算出体积为10.此题的最大障碍就是准确判断几何体的形状，即要准确实现三视图向直观图的转化，只有画出直观图，而不仅仅是由三视图想象几何体的形状.

图6

图7

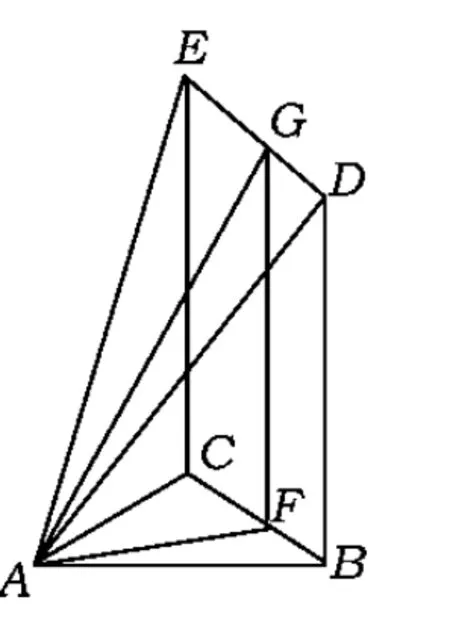
图8

突破口首先画出三棱柱的直观图(如图6所示)，然后去掉一个大三棱锥，得到一个四棱锥体(如图7所示)，其底面是一个边长为5的正方形，其高为.于是其体积为

变式若某几何体的三视图(单位：cm)如图5所示，则该几何体的表面积为 .

此几何体的表面有5个面，其中4个面为特殊面(1个正方形、3个直角三角形)，第5个面为任意△ADE，如何求此三角形的高或面积呢?

(3)如图8所示，由AF⊥BC，过点F作FG∥BD，联结AG，则△ADE的高于是

对于学生而言，看似一个非常简单的问题，充满活力的是求解的各个思路，寻找最佳思路是一个展示数学智慧的机会!

3 三视图的基本投影模型的再现

例4某几何体的一条棱长为，在该几何体的正视图中，这条棱的投影是长为的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为a和b的线段，则a+b的最大值为 ( )

障碍点(1)一条线段的投影的三视图位置联系;(2)投影的三视图与直观图中的数量关系;(3)基本不等式的运用.

突破口人教A版《数学(必修2)》第12页给出一个长方体在3个方向上的投影——三视图，这其中蕴含着一条线段(长方体的体对角线)在3个不同方向上的投影，这种思维的联系是学生最缺少的.设此长方体的长、宽、高分别为 x，y，z，则

当且仅当a=b=2时等号成立.

此问题检测学生的基本投影模型的再现能力、数学建模能力、数据处理能力，而有关三视图的教学需要增加这方面的训练!

图9

4 实物、直观图、三视图间转化

例5如图9，单位正方体ABCD-A1B1C1D1中，E，F 分别是BC，CD的中点，平面 A1EF交BB1于点M，交DD1于点N.

(1)画出几何体A1MEFN-ABEFD的直观图与三视图;

(2)计算几何体A1MEFN-ABEFD的体积;

(3)计算几何体A1MEFN-ABEFD的表面积.

障碍点(1)在正方体中是否能准确画出平面A1EF(学生最容易画成△A1EF);(2)是否能准确画出几何体A1MEFN-ABEFD的直观图;(3)画三视图时，实线、虚线是否准确画出;(4)如何分割几何体成为基本空间几何体并计算出体积;(5)如何准确地计算各面的面积.

突破口(1)已知几何的直观图如图10所示，三视图如图11所示.

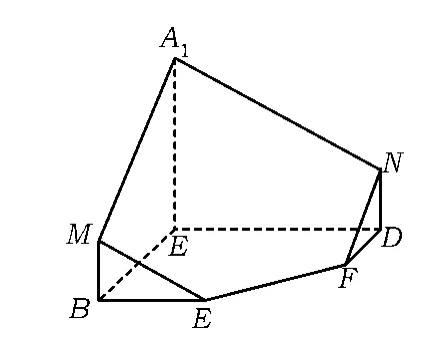
图10

图11

(2)几何体A1MEFN-ABEFD是一个六面体，有多个思路可以计算其体积：①先补形成大三棱锥并计算其体积，再减去2个等积小三棱锥的体积;②将其分割成2个等积的四棱锥和1个三棱锥，从而

(3)几何体A1MEFN-ABEFD是一个六面体，根据其对称性，只要计算2个梯形、2个三角形和1个五边形的面积，从而

例6一个棱锥的三视图(单位：cm)如图12所示，则该棱锥的全面积为 ( )

图12

(2009年宁夏、海南省数学高考试题)

障碍点(1)根据三视图想象不出直观图的特征或画不出直观图;(2)把三视图中某一边(本是直观图中某一面上的斜高)当成侧棱或反之.

图13

突破口首先根据三视图来还原几何体的直观图，根据俯视图画出三棱锥的底;然后根据主视图与侧视图确定三棱锥的高，由于俯视图与主视图的对称性，可判断高PO的位置;最后联结 PA，PB，PC，得到三棱锥的直观图.如图13，根据三视图中的数据，有 PO=4，OD=3，由勾股定理得

从而全面积为

故选A.

将三视图转化为直观图，除了能画出直观图以外，还要能分析直观图与三视图中的数量关系.