由一道向量填空题谈解题思维的教学实践

●王 耀 (田家炳实验高级中学 江苏苏州 215006)

由一道向量填空题谈解题思维的教学实践

●王 耀 (田家炳实验高级中学 江苏苏州 215006)

与三角形联系的平面向量基本运算问题是数学高考中经常出现的一类题型.对这类题型的教学探究可以开阔学生的解题思路，培养学生的分析思维，提高学生解决问题的能力.本文利用一道数学高考模拟试题，从学生实际出发进行创新教学思维的尝试，有效地创设了学习空间，让师生都能获取“智慧”，从而寻找到问题解决的策略.

1 试题再现

试题

在面积为1的△ABC中，E，F分别为AB，AC的中点，点P在直线EF上的最小值是＿＿.

2 思维的落实与衔接

这道题短小精悍，个性鲜明，内涵丰富，乃整张试卷中的一个亮点.命题者以三角形中量的关系为背景，将平面向量的数量积和不等关系融为一体，具有一定的思维量.因此，首要任务就是要利用好已知条件，将数学语言用图形语言直观地表达出来.此时得到第一个信息：点P在边BC的中位线上.因此，解决这个问题的切入点就落在表达式的转化问题上.一般情况下，看到这个表达式会联想到哪些相关信息呢?

基于上述层层深入的联想信息，解题的落实(起)点和衔接(承)处已经联系自然，可得如下解法：

(1)数形结合法：设 A(0，2)，B(cosx，－sinx)，则f(θ)表示AB所在直线的斜率，利用图像可得

当且仅当α=30°时，等号成立.

3 思维的转换与整合

众所周知，向量具有二重性，可以从“代数运算”角度分析，也可以从“几何图形”角度去思考，这正是部分学生试图建立平面直角坐标系转化问题的原因.然而，该题只知道△ABC的面积，如何设坐标呢?“那就设长度!”这是大部分学生头脑中立马会出现的想法.如此思维转换，便可带来一种新的分析途径：

学生发现PD还是BC的中线，则由PD是中垂线发现△PBC为等边三角形.因此，该问题的本质是：在面积为定值的三角形中，正三角形边长的平方和最小.这与著名的“等周定理”相似，等周定理中有一条是：在面积为定值的三角形中，正三角形的周长最小.

既然结论已经明了，那么能否再换个思路：考虑利用三角形3条边之间的不等式关系去证明这个结论?有学生经过化简变形后得到ab+bc+然后利用Cauchy不等式和Jensen不等式得到如下简洁解法：

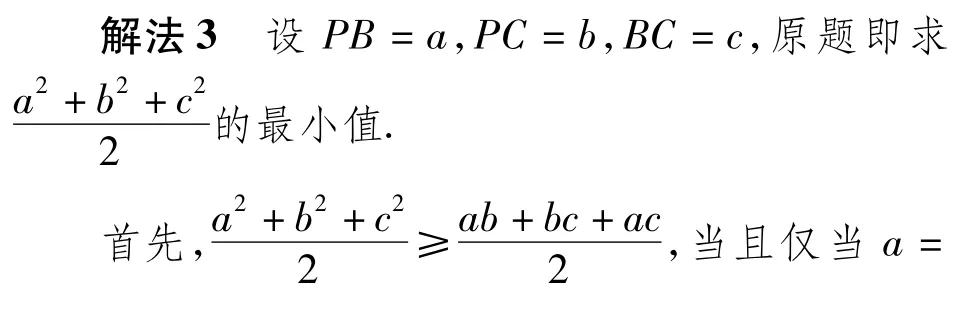
当且仅当P=B=C时，等号成立.

学生的兴致越来越高，想不到一个小小的填空题竟有如此玄机，真可谓“题目虽小，其容乃大”啊!令人意外的是，有些学生提出了异议：上述的解法3用的是数学竞赛方面的方法，教材中没有涉及这些著名的不等式，这一异议同时招致了“群众”的附和.在课前准备时，笔者没有想到会出现这种意外的状况，这出“戏”该如何收场?稍作调整，笔者只好谦虚地表示很愿意与学生一起尝试，于是就有了以下源于教材的解法：

此时下课的铃声响了，学生们仍然兴奋不已，笔者偷偷地长舒了一口气，顺势回忆了这道题的来龙去脉，即从解题思维的起点与走向作了重点回顾，再次与学生们分享这道高性价比的小题.

4 几点思考

4.1 数学教学探究环境应构建“生态和谐化”

生态和谐和生态平衡是一个已取得全球化共识的当代人类主题.笔者认为这一理念有必要移植并借用到数学课堂教学中来，努力追求“生态和谐”的课堂氛围.在课堂教学活动中，教师应充分尊重学生的主体地位，努力营造和谐、民主的课堂教学情境，实现师生情感的和谐共振.数学解题教学是数学教学的一个重要组成部分，在解题中应通过恰当的教学方法、合理的教学设计让学生主动参与进来.对学生多一份等待、多一点激励、多一句鼓舞.只有这样，才能激发学生的学习兴趣，使学生愉悦地学习，积极主动地参与教学活动.

4.2 数学解题分析过程应推崇“思维自然化”

自然化的数学解题思维是朴实的思维.只要按“步”就班地进行分析、联系、转化，就能解决问题，在解题过程中淡化对解题技巧的依赖.这种措施也能在很大程度上让学生避免陷入“题海”战术.那么，如何培养学生的思维自然化?笔者认为，首先教师自身应加强专业素养，在教学实践中更新教育教学理念和方法.其次，教师在分析问题时，努力从学生的认知结构和思维层面去研究教法，这样才能在课堂上构建师生思维上的共鸣.本节课中，笔者将一道题的来龙去脉自然呈现，被学生自然地理解并内化，只有这样学生才能逐渐学会如何进行有效而有序的思维.

4.3 数学课堂预设过程应提倡“综合多元化”

新课改所需要的理想课堂应该是“以生为本”的课堂.于是，当思维迥异，个性纷呈的学生聚集在一个教室，教师应如何预设才能使课堂充满生成性?笔者认为，教师应努力做到预设过程综合多元化.首先，预设学生，即从学情差异、质疑困难、思维变换、延伸拓展方面去预设;在课堂教学中，还要预设教师，虽然教师把自己的思维真实地呈现给学生，可以让学生感受到教师的思维，但是教师要学会倾听，给学生表达思想、展示解法的机会.另外，