高效缘于“让位” 精彩缘于“生动”——以一节高三数学高考备考研讨课为例

●刘亚平 高 敏 (睢宁高级中学南校 江苏睢宁 221200)

高效缘于“让位” 精彩缘于“生动”
——以一节高三数学高考备考研讨课为例

●刘亚平 高 敏 (睢宁高级中学南校 江苏睢宁 221200)

最近徐州市中学数学学科名师经验交流会暨高考备考专题研讨会在睢宁中学南校召开，受徐州市教育局的安排，笔者所在学校高敏教师开设了一节高考备考专题观摩研讨课——“运用函数、方程、不等式思想及放缩法证明不等式”.考虑到学生对数学思想及解题技能有了一定的掌握与理解，因此没有把内容设计成一堂“杂烩”课，而是希望沿着2个例题和1个链接讲清一类问题，理顺一种思想，充分利用学生已有的知识经验，从解题的矛盾冲突中激发生“动”，达到用思想指导方法的解题习惯.现将本节课的教学过程呈现如下，以供与大家交流.

1 教学实录

教师：在历年各地的数学高考试卷中，与不等式相关的试题所占的比例更是“居高不下”，低、中、高3档题目均经常与不等式挂钩;许多把关试题，特别是体现试卷区分度的“压轴题”，常与不等式有关.解答这类问题需要频繁地运用各种基本数学思想，对树立、巩固、强化与熟练运用这些数学思想极为有益.例1着重考查运用函数、方程、不等式思想及放缩法来证明不等式.

例1已知函数f(x)=lnx.

(1)求函数g(x)=f(x+1)－x的最大值;

(2)当0＜a＜b时，求证：

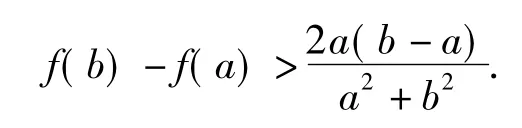
给学生6分钟时间思考、讨论与交流.第(1)小题：gmax(x)=g(0)=0(解题过程略).对于第(2)小题，由于教师指明了解题的思路，大家跃跃欲试，很快就有学生1得到的解法.

故原不等式得证.

教师：学生1很睿智也很坚强，说他睿智是因为他“就地取材”地构造了函数;说他坚强是因为在求复杂的导函数H'(x)时，他没有被“气势汹汹”的复杂计算所吓倒.

(教师的激励言语增强了学生1的信心和成就感，更把课堂气氛推向高潮.)

学生2：在不等式中，字母a，b的地位是均等的，既然可以用b作为自变量构造函数，那么也可以用a作为自变量构造函数

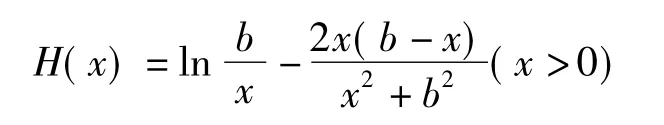
应该也行得通(解题过程略)!

教师：学生2的洞察力很强，他巧妙地运用轮换思想“克隆”了函数，可见“克隆”也是一种创造啊!

在总结此解法时，一位学生说：我也是这样构造函数的，但求导函数求错了;另一学生说：我求导函数求对了，但对导函数变形时出错了，没有判断出函数的单调性，真有点遗憾.

教师：学生1和学生2都是从a，b中选定一个字母的全部位置作为构造函数的自变量位置来构造函数，给求导函数带来了困难.能否选定字母的部分位置作为

(教师的提示还没有说完，学生的思路瞬间被打开.)

学生3：从a，b中选定一个字母的部分位置作为构造函数的自变量位置来构造函数，令

通过讨论大家很快认识到虽然这4种函数都是单调函数，H(b)与H(a)的大小关系确定，但由于H(b)与H(a)都不等于0，得不到所要证明的不等式，因此不能只把其中一个位置上的字母作为自变量来构造函数.

教师：直接构造函数像把“双刃剑”，杀敌一千，自损五百.根源在于我们没有对原不等式进行更好、更优地等价变形，直接法构造的函数形式有点复杂，导致求导函数计算量较大.

(教师的总结刚结束，还未平静的学生瞬间又兴奋起来.)

教师：上述3位学生都是利用对数运算法则和不等式性质对原不等式进行等价变形，可谓稳扎稳打，很值得大家学习.但由条件0＜a＜b和要证明的不等式中含有a2+b2，大家想到什么公式?能否先利用此公式把不等式放缩后再构造“升级版”的函数呢?

学生9：运用公式放缩法.要证

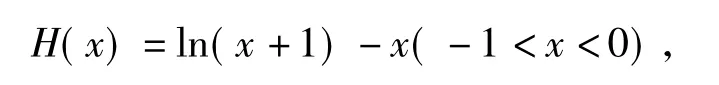
再结合例1第(1)小题的结论，可证原不等式成立.

教师：已知2个正数a，b之和或之积或平方和，那是运用基本不等式放缩的一个“招牌式动作”.这3位学生的解法也告诉我们一个事实

学生：“高风险才有高回报”啊!

(学生忍俊不止，在欢声笑语中对基本不等式放缩的重要性有了深刻认识.)

学生：多么简洁、精致的一个函数!这比运用基本不等式放缩更容易想到!

(正当大多数学生由衷感叹时，思维敏捷的学生13发现了问题所在.)

教师：学生12的字母放缩法很精妙，但放缩后构造出的函数没能如愿发挥应有的作用，这是为什么呢?

学生：可能是放缩过头了吧!

教师：是的，学生12放缩的幅度太大了，以致于放缩后构造“最简单”的函数失去了应有的威力.因此，在利用放缩法时要时刻注意放缩的幅度.(学生茅塞顿开，频频点头)看来大家对放缩法的使用还不能得心应手，再看例2.

例2已知数列{an}的通项公式an=3n－2n.求证：对一切正整数n，有

(2012年广东省数学高考理科试题第19题改编)

首先教师用多媒体把例2的标准答案(共2种方法)逐一展示出来(略)，让学生自主归纳证明这类不等式的通法：通过放缩法把数列变成一个能求和的数列.紧接着又把学生分成8组，每组6人，教师参与其中引导学生对2种标准答案进行类比、提炼，并提示学生探索有没有其他的放缩方法.整个教学过程教师本着“关注学生所想，激励学生大胆猜想，给学生尝试机会”的教学策略，取得了意想不到的教学效果，学生感受颇深，收获颇多，得到了五彩缤纷的放缩方法.

最精彩的部分在于能否运用数学归纳法证明此不等式.因为把假设n=k的内容直接代入n=k+1的式子无法进行，所以一些学生认为不能;而另一些学生认为一定能，但找不到运用假设的切入点.最后在教师循循善诱的启发下，学生终于发现了解题的突破口：因为在n=k+1的式子中除了第1项外，其余的项数和假设的项数相同，所以只要运用数字放缩法即可，如

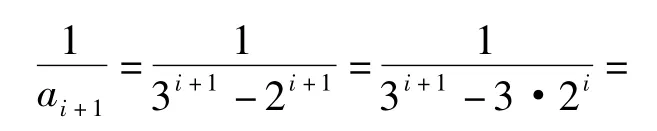
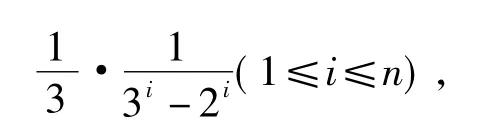
在其余的项中“提取”出假设(解题过程略).

2 高考链接及课堂小结(略)

3 专家点评

黄安成(江苏省数学特级教师)：因为学生是学习的主体，所以开展解题教学活动的根本目的是：培养学生主动思考与主动探究能力，实现学生对知识系统、方法体系、思想提炼的自主建构.要突出学生的主体地位，教师就应该充分尊重学生真实的解题经验，在开展解题教学过程中，要注意研究学生的解题经验中已有的个人经验和原始观念，思考学生经验中是否有足够的理论支撑当前的解题，使学生的解题始于学生“现有发展区”，然后熟练驾驭解决问题的“制高点的思维区”.

例如在讲解例1、例2时，首先从学生最初的思维起点——“构造函数法”出发，鼓励学生大胆尝试，当学生思维受阻时，教师并没有一语道破“天机”，而是采用了“点到为止”的教育机智，让学生感受思维受阻的缘由，亲身打磨“放缩法”使用的心路历程.在得到例1的10种“构造函数法”与例2多种“放缩法”的过程中，教师始终以协作者的角色参与其中，让学生说思路、讲道理、亲实践、多反思，没有抢学生的“镜头”，主导地位发挥适当，教学效果十分显著.

袁宝金(江苏省数学特级教师)：通过对“提出问题—分析问题—解决问题—归纳总结”流程的反复使用，不但使学生的知识得以升华，学习欲望得到提高，而且培养了学生严谨的思维习惯，通过问题情境的设置把部分问题的错解与正解进行辩证分析，使学生对这类题型有了更深层的理解，提高了学生思维的深刻性、严谨性与批判性.虽然例1、例2的证明方法迥然不同，但它们都有相同的关联点——放缩法的使用，顺理成章地形成一个知识体系，符合学生的认知规律.

难能可贵的是，教师在引领学生从例2的2种标准答案中把方法提炼出来后，并没有就此结束，而是顺应学生思维的需求，对“放缩法”使用的技巧给予进一步诠释;对数学归纳法的合理运用给予完美展示.教学过程跌宕起伏、峰回路转，令学生赏心悦目、沁人心脾、拍案叫绝.

魏贤刚(徐州市数学教研员)：这是一节高效的高质量的高考备考专题复习课，它着重讲解了函数、方程、不等式思想及放缩法等在证明不等式中的应用.教师在讲解例题前，首先详细地介绍了不等式试题的类型、难度与解决策略，为学生证明不等式营造积极的求知氛围.紧扣《普通高中数学课程标准(实验)》的要求，以“问题教学法”为主线，收放自如，引导学生主动探索，体验数学发现和构建的过程，通过对“问题链”逐个释疑，使学生的解题思想逐趋合理、解题方法渐臻完善.整堂课简约而不简单.

4 听课启示

这节课教师只带领学生详细地解决了2道例题，一个链接，少而精!这与笔者此前所见到的一些教师的教学过程不同，在当前的高三数学专题复习课中，一个很普遍现象是课堂容量大、节奏快，学生疲于奔命，教师苦不言堪.当学生看到题目后，教师往往只留给学生很短的思考时间，就开始滔滔不绝地讲解，不敢把时间还给学生，生怕完成不了课堂任务;不愿意把机会让给学生，担心学生的思维出“差错”，追问出“岔道”，影响原本预设好的教学轨迹.教师要领悟新课改精神，处处为学生着想，让位于学生，让学生成为课堂的真正主人”.当然要想让学生成为课堂的真正主人，还需要教师具备渊博的专业知识、先进的教学理念、娴熟的教学技能、幽默的教学语言，只有这样教师才能感召学生想动、敢动、乐动，教学才能真正达到“放马于原野之中，牵其于晚霞之时”的潇洒境界，演绎多维精彩的高效课堂.

［1］程爱文.让学生的心灵去旅行——一堂试卷评课教学［J］.数学通讯，2011(8)：19-23.

［2］吴少然，王克亮.“生动”课堂的一种诠释是生“动”——一节省级公开课“抛物线的标准方程”的课例及启示［J］.中学数学教学参考，2011(4)：20-23.

［3］张传鹏.关注数学思维演绎精彩课堂——习题课有效性教学的一点探索［J］.中小学数学，2013(1/2)：58-60.